一類分數階微分方程組無窮點邊值問題正解的存在性

陸心怡

（池州學院數學與計算機學院，安徽池州247000）

1 引言

近年來，分數階積分以及分數階微分方程理論越來越多的運用在各個領域,在流體力學、化學、工程學、生命科學等方向有著廣泛且重要的應用，作為非線性分析的一個重要分支，很多學者也非常熱衷于研究分數階微分方程正解的存在性和唯一性以及變化的多樣性.且經過實際檢驗,相對來說分數階模型比整數階模型應用的領域可能更加寬泛和精確[1]，對于研究結果的準確性有著很大影響.

本文用Leray-Schauder非線性抉擇性來研究下面的分數階微分方程組無窮點的邊值問題：

n-1＜α,β≤n,i為固定常數，i∈N,i≤n-2,α,β≥2.是連續函數,是黎曼劉維爾形式的,其中

2 預備知識和引理

首先給出相關的定義、引理以及定理等.

定義1[2]函數的 i∈N,i≤n-2,α≥2,階Riemann-Liouville積分定義如下

0＜t＜1,n-1＜α≤n,，

其中右邊是在ηj≥0上逐點定義的.

定義2[2]函數的0＜ξ1＜ξ2＜…＜ξm-2＜1,階Riemann-Liouville微分定義如下

引理1[3]設 α＞0,假設u∈C(0,1)?L(0,1),那么微分方程有唯一解其中 n 是不小于 α的最小整數.

引理2[3]對于一個α(α＞0)階分數階微分,給出那么

其中n為不小于α的最小整數.

注[2]α(α＞0)階的Riemann-Liouville微分和積分有以下性質：α,β＞0,u∈L(0,1).

引理3設 f∈C[0,1],n-1＜α≤n,i為固定常數,i∈N,i≤n-2,α≥2.那么微分方程

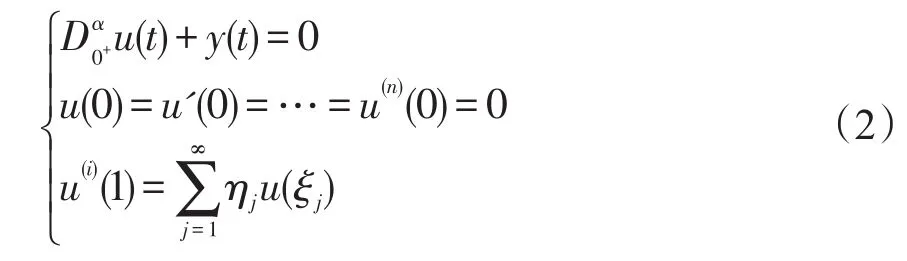
有唯一解

其中

證根據引理1,首先，將(2)中的微分方程轉化成與之等價的積分方程

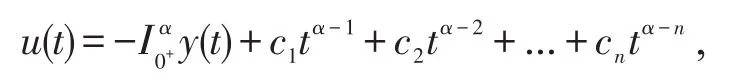
由u(0)=u'(0)=...=u(n-2)(0)=0,得c2=c3=…=cn=0.即

那么

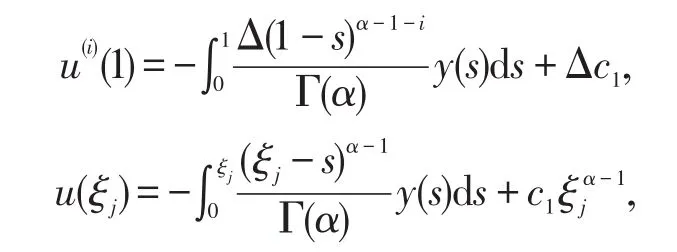
因此,

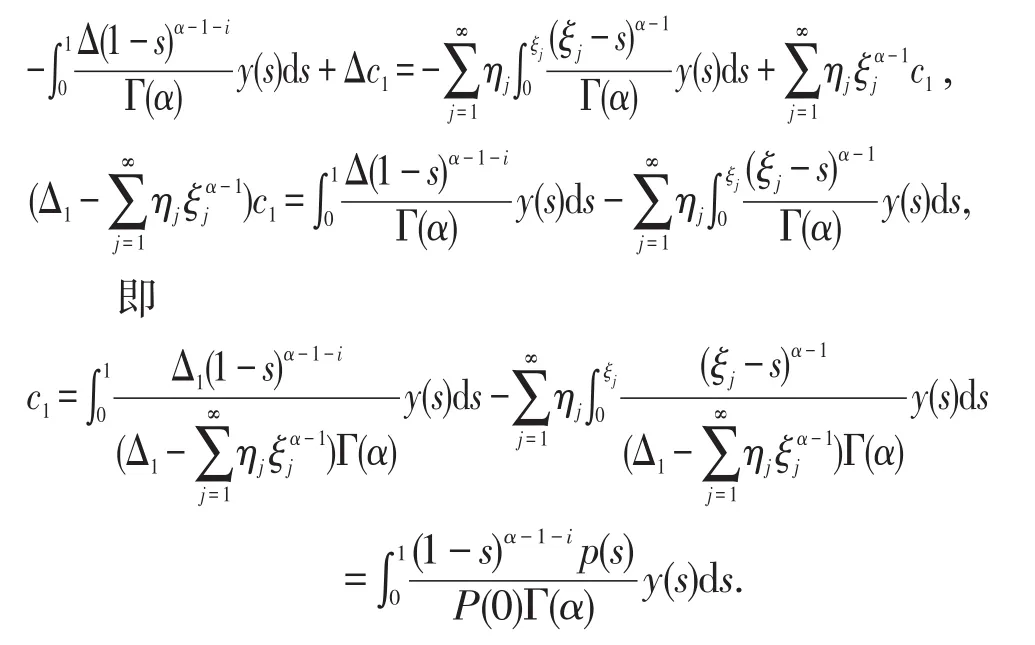
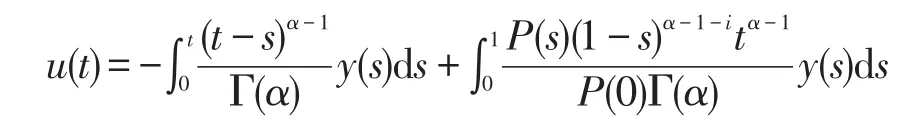
則微分方程（2）的唯一解是

得證.

引理4P(0)＞0,P(s)滿足以下兩個條件：

a.P(s)在[0,1]上單調增且恒成立;

b.存 在 M1≥m1≥0 使 得 任 意有m1s+P(0)≤P(s)≤ M1s+P(0).

證a容易算出 P'(s)≥0,因此P(s)單調增,又P(0)＞0,知 P(s)≥P(0)＞0;

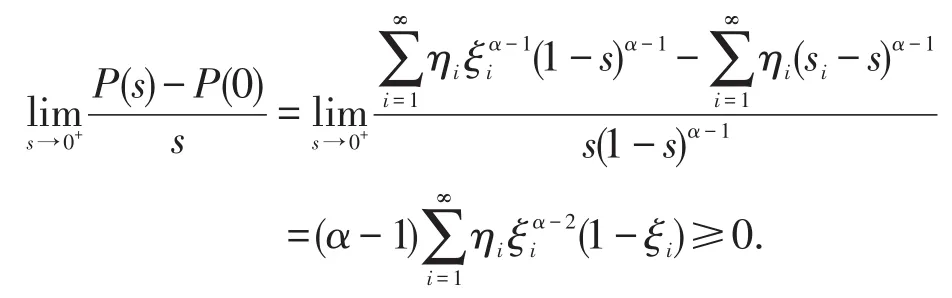
并且 M1≥m1≥0,且m1s≤P(s)-P(0)≤M1s,?s∈[0,1].

引理5由（3）定義的函數G(t,s)具有以下性質：

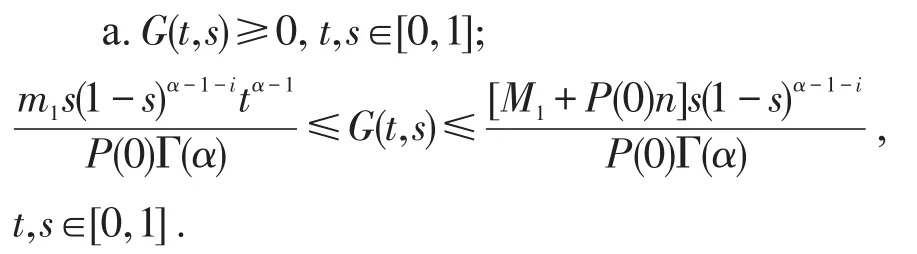
證明略[1].

引理6[4](抉擇性)E是Banach空間,C是E中的凸閉集.假設U是C的相對開子集,0∈U且是連續開子集.則下列條件：

a.A在U中有一個不動點;或者

b.存在u∈?U,λ∈(0,1)使得u=λAu;

成立。

3 主要結果

引理7[1]設是連續函數,且滿足假 設 存 在0＜σ＜1使得 tσF(t)在 [0,1]上是連續函數.那么是連續函數.

那么方程組（1）可以轉化成下面的方程：

該部分的證明可由[5]中的引理3.3得出.下面來定義一個算子A:X×X→X×X

引理 8[1]令 n-1＜α,β≤n,i為固定常數,i∈N,是連續函數并且滿足假設存在 0＜σ1＜1使 得在 [0,1]×[0,+∞)是 連 續 函 數,則A:P→P是全連續算子.

（2）存在r＞0,有

那么方程組（1）存在一個正解.

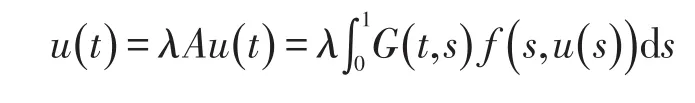
所以,

綜上所述,由引理6可知存在不動點u∈Uˉ,v∈Uˉ因此方程組（1）存在一個正解.