基于改進遺傳算法的限容量多旅行商問題研究

束東來，張玉州

（安慶師范大學 計算機與信息學院，安徽安慶246133）

限容量多旅行商問題（LCMTSP）是對經典旅行商問題（TSP）及多旅行商問題（MTSP）的模型擴展。

實際問題中讓一個人從一個城市出發去拜訪若干個城市，其工作量是巨大的，所以考慮到工作效率等問題，MTSP更符合實際，而每個旅行商的精力是有限的，安排一個合理訪問城市個數的范圍是有必要的[2]，LCMTSP問題在MTSP問題基礎上，給每個旅行商施加了一個訪問城市個數的限制條件，顯然更符合實際意義。

本文以3個旅行商、每個旅行商訪問城市不少于3個但不多于10個、從一個城市出發訪問其余19個城市并回到出發城市問題為例，對傳統的遺傳算子稍加改進，實驗證明能夠較好的解決限容量多旅行商問題。

1 LCMTSP數學模型

帶有容量限制的多旅行問題是在原有的多旅行商問題的基礎上多了一個容量限制的約束條件。其目標函數為m個旅行商所走的路程最短，其約束條件為m個旅行商中每個旅行商訪問城市的個數有上下限。

本文模型與基本TSP問題一樣，是尋找加權圖中最短回路問題[4]，假設城市號從1～n，其中城市1為出發城市，m個旅行商。

定義變量：

其中i=1,2...N，k=1,2...M

目標函數為：

約束條件：

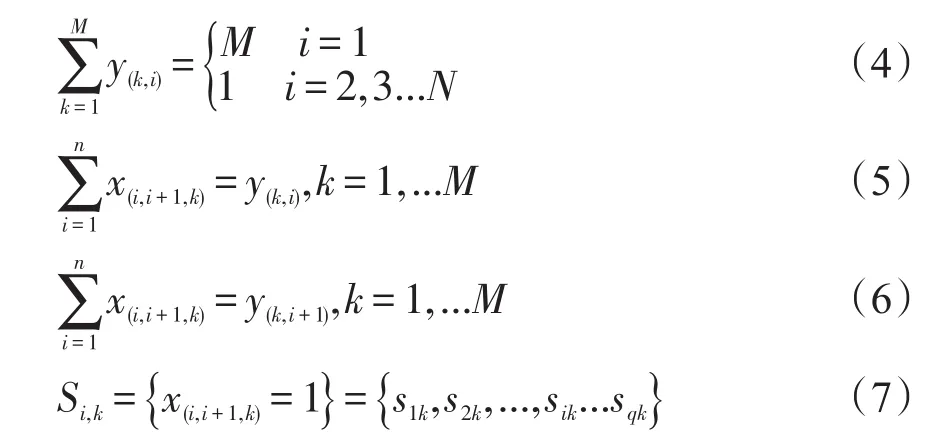
其中Si,k為第k個人訪問的城市的合集，sik代表第k個人訪問的第i個城市，q代表訪問者訪問的城市數目

公式（4）代表從指定城市1出發，所有城市僅有1個訪問者嚴格訪問一次；

公式（5）表示任意一條路線的次終點城市（iq,k）僅有一個起始點城市與之相連；

公式（6）表示任意一條路線的起始點城市僅有一個次終點城市（iq,k）與之相連；

公式（7）表示第k個訪問者訪問的所有城市；

公式（8）表示所有訪問者訪問的城市總和；

公式（9）每個訪問者最少訪問a個城市，最多訪問b個城市；根據本文20個城市、3個旅行商、每個旅行商訪問城市個數不少于3個且不多于10，約束條件（9）改為3≤q≤10。

2 遺傳算法設計

2.1 編碼

本文采用以遍歷城市的次序排列的一種染色體自然編碼方法，即一個解序列表示一條染色體。如串碼0-1-2-3-4-5-6-7-8-9-0表示自城市0開始，依次經1，2，3，4，5，6，7，8，9，遍歷路徑，最后返回城市0[5]。

如城市為0，1，2，...，19的三個旅行商問題的一條染色體編碼為：

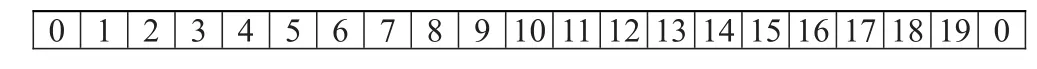
其中斷點分割隨機斷點r1、r2；如r1=6，r2=12：

將斷點r1、r2插入染色體編碼中，斷點的選擇會受到問題容量限制條件的約束，每個旅行商訪問城市個數為不少于3個且不多于10個。

則三個旅行商的路徑分別表示為：

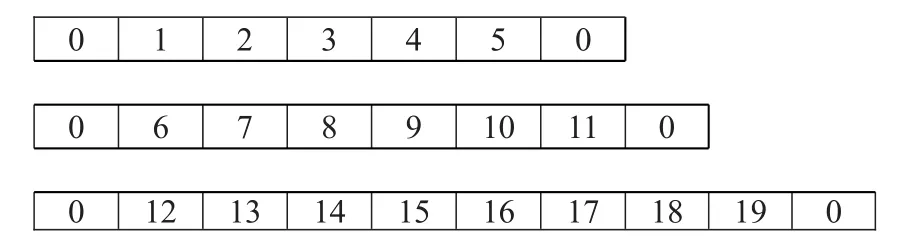
2.2 群體規模

合理的群體規模對遺傳算法的收斂具有重要意義[6]，群體規模太小難以得到滿意的結果，群體規模太大會使計算復雜。根據經驗，本文群體規模取100。

2.3 適應度函數

適應度函數是根據個體的適應值對其優劣判定的評價函數。在旅行商問題中用訪問路徑的總距離的倒數作為適應度函數來評價求解結果是否最優[7]。即：

2.4 初始化種群及初始化父代

2.4.1 種群初始化 產生一個sizepop×19的數組，每一行存儲一個序列；產生隨機斷點，存儲在sizepop×2的數組；把對應的斷點加入初始化數組中，求出sizepop×19個體中最優的記錄對應序列反下標。2.4.2初始化父代 初始化父代采用完全隨機（inti_rand_nerb）與次優選擇(init sub sele)相結合的方法。產生一個隨機數，如果生成的隨機數是0，就采用完全隨機的方式一個父代；如果生成的隨機數是1，就采用最近鄰法生成一個父代。

在完全隨機方法中，首先產生一個1～19的一個隨機數作為序列的第一個元素，然后依次循環產生此序列的下一個元素，在每次產生下一個元素的時候判斷是否與此序列中前面產生的元素相等，若相等則重新產生，否則添加到序列中；然后再進行斷點分割，分成三個旅行商的訪問路徑。

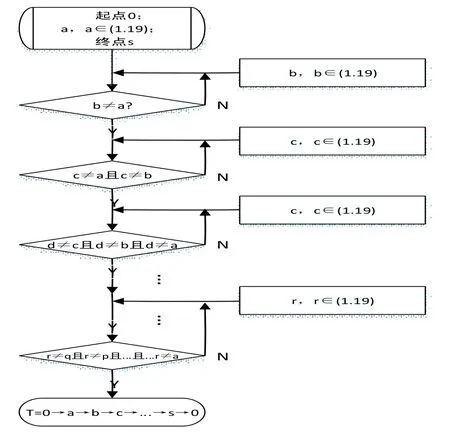
圖1 完全隨機法初始化父代

在次化選擇法中，首先產生三個0～2的隨機數，看作對應的旅行商，若當前產生的隨機數為0，則在候選集合中選取距離第一個旅行商次近的城市，并添至其路徑中，直到候選序列為空。例如下圖2：

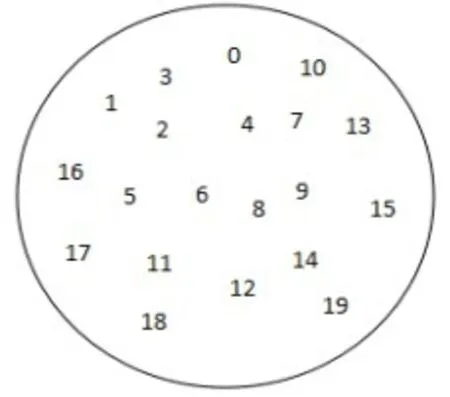
圖2 次優選擇法初始化父代

0為起始城市；

1,2,3 ,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19為需要訪問的城市；

三個旅行商分別為T1、T2、T3；

產生一個0～2的隨機數r；

計：r=0，選擇未被選擇的城市中距離T1所在位置次近的城市；

計：r=1，選擇未被選擇的城市中距離T2所在位置次近的城市；

計：r=2，選擇未被選擇的城市中距離T3所在位置次近的城市。

2.5 控制容量操作

根據本文容量限制這一約束條件，控制每個旅行商訪問城市個數范圍：3≤q≤10；產生一個length×19的旅行商，隨機產生一個3～10之間的隨機數，作為第一個斷點；再產生另外一個隨機數，使得與前面產生的隨機數的距離大于3且與終點的距離大于3且不大于10，作為另一個斷點。

2.6 選擇操作

在群體大小為n的群體中，如果一個個體i的適應度為fi，則該個體被選擇的概率，然后對各個染色體計算它們的累積概率，概率Pi表示個體i的適應度在群體的個體適應度總和所占的比例，個體適應度大的被選擇的概率就越高[9]。

運用輪盤賭法選擇較優個體，為了選擇父代需要進行多次選擇，每次產生一個[0,1]的均勻隨機數，將該隨機數作為選擇指針來確定備選父代個體。

2.7 交叉操作

交叉算子是遺傳算法里面的核心算子。交叉算子里面的交叉概率的設置較為重要，交叉概率大能增強遺傳算法開拓新搜索空間的能力，但有可能會破壞一些性能較好的基因串，而交叉概率小又會引起算法遲鈍。本文交叉概率取0.8。

對于LCMTSP問題，本文交叉算子采用PMX算子、OX算子、CX算子以及最小路徑交叉規則等算子與斷點分割過程相結合。

部分匹配交叉算子（Partially Matched Crossover，PMX）是針對TSP問題提出的基于路徑表示的交叉操作，先均勻隨機分布兩個交叉點，定義這兩個點之間的區域為匹配交叉區域，使用位置交換操作將兩個父代該區域進行交換，交換出現重復的部分用原基因位的數字代替[10]。

順序交叉算子（Ordered Crossover，OX）是針對TSP問題提出的基于路徑表示的交叉操作，該算子能夠保留排列并融合不同排列的有序結構單元[11]。兩個父代交叉時，選擇其中一個父代的一部分，保存另一個父代中代碼的相對順序生成子個體。

循環交叉算子（Cycle Crossover，CX）也是針對TSP問題提出的[12]，循環交叉操作中子代的代碼順序根據其任意父代個體產生。

最小路徑交叉規則(Minimam Puth Crossover,MPC)是本文在三個旅行商之間操作的一種交叉算子，根據斷點分割后的三個旅行商，用產生的隨機數對其中兩個旅行商進行交叉互換操作。例如：

一條父代的染色體編碼為：

產生兩個隨機數r1、r2∈（0,2），如r1=0、r2=1就旅行商A與旅行商B進行交叉；計算旅行商A與旅行商B中旅行商訪問城市少的城市個數，如上所示，旅行商A訪問城市個數為6，旅行商B訪問城市個數為9，選擇L=6（L為需交叉的路徑長度）；產生兩個隨機數q1、q2∈（1，6），如q1=2，q2=5，對旅行商A、B進行交叉互換：

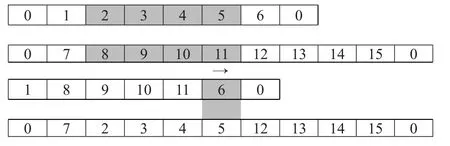
2.8 變異操作

變異算子在遺傳算法中屬于局部搜索操作，其目的是維持種群的多樣性。變異算子里的變異概率也較為重要，較低的變異概率能防止種群中優良基因的丟失，但是降低了遺傳算法開拓新搜索空間的能力[13]，而較高的變異概率又會降低算法的收斂度和穩定性。本文變異概率取0.01。

對于LCMTSP問題，本文變異算子采用SWAP算子、2-opt算子、3-opt算子以及SI、DI算子與斷點分割過程相結合。

SWAP算子是兩點對換算子，將位置r1，r2，將這兩個位置的數字進行對換。

2-opt算子是為了加速進化而加入的一個操作，具有單向性，即只有逆轉之后個體變得更優才會執行2-opt操作，否則逆轉無效[14]。根據小路徑取反原則，產生[1,19]之間的兩個位置r1、r2，將r1和r2之間的基因序列進行反向排序。

3-opt算子是在2-opt算子的基礎上又選了一個逆轉點，產生[1,19]之間的三個位置r1、r2、r3，將離第一個城市最近的位置點與第一個城市位置點之間的序列進行反向排序，將后兩個位置點之間的基因序列進行反向排序。

SI算子是一種單插入變異算子，將路徑中一個位置r1的數刪除，插入該路徑的另一個位置r2前面。例如：

一條父代的染色體編碼為：

DI算子是一種雙插入變異算子，它將路徑中連續兩個位置r1、r2從當前位置刪除，插入該路徑的另一個位置r3前面。例如：

一條父代的染色體編碼為：

本文考慮到所有位置變異情況，即上述5種變異算子中每一個點都要進行測試，即遍歷所有可能的情況，選擇最優的過程，算改變后的總距離，然后選取最優的解（總距離最短），遺傳到下一代。

3 實驗結果及分析

本文借助 C 語言，在 Intel（R）Core（TM）i5-6500 CPU處理器計算機環境中對LCMTSP問題的遺傳算法進行研究，用3個旅行商訪問20個城市的LCMTSP實例進行測試，選取100個染色體作為初始種群，最大遺傳代數為1000，交叉概率為0.8，變異概率為0.01。

實驗對程序進行了運行10次、20次、50次、100次，將本文提出的模型與原始MTSP模型進行對比，并對實驗結果進行分析，取實驗結果的平均值及最小值的方法來提高實驗的準確性和可信度。

實驗對LCMTSP問題進化代數100、300、600、1000、1500代進行了實驗，取實驗結果的平均值及最小值的方法來提高實驗的準確性和可信度。

實驗結果如表1和表2所示：

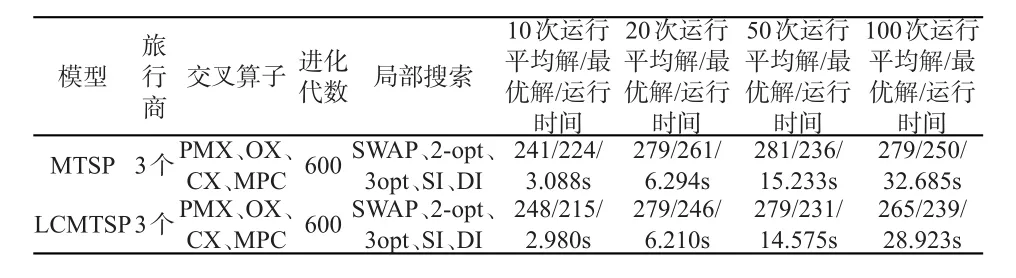
表1 LCMTSP與原始MTSP實驗對比

表2 gen=100、300、600、1000、1500代時的解、運行時間

借助Matlab2014a軟件，程序運行一次，LCMTSP模型進化軌跡圖如圖3-圖8所示：

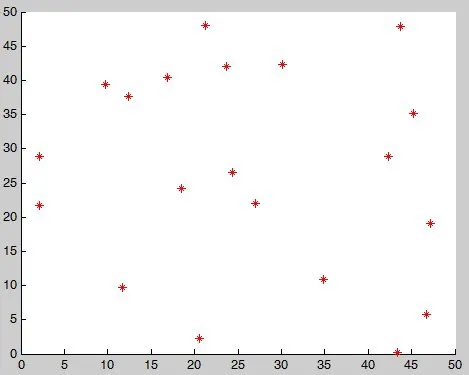
圖3 種群初始化

圖5 gen=300，l=341.893153

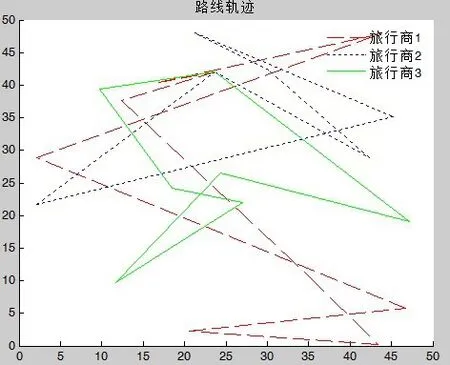
圖6 gen=600，l=289.967866

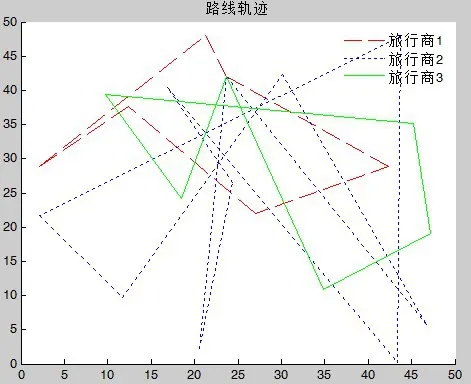
圖7 gen=1000，l=250.927191

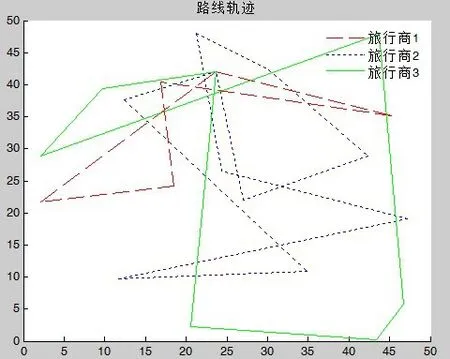
圖8 gen=1500，l=279.258567

從程序運行結果可以知道，由于遺傳算法是一種啟發式算法的特性，每次運行的結果大都不相同但都相近。

從實驗結果最優解與平均解可以看出本文限容量多旅行商問題與傳統多旅行商問題實驗結果總距離差距不大甚至更優。

從實驗運行時間來看，本文模型運行時間比傳統多旅行商問題運行時間稍短。

從實驗對LCMTSP問題進化代數來看，在進化到1000代左右時，總距離基本已經可以達到最小值，再進化更多代數總距離無明顯改進。

綜合實驗結果與實際意義，本文提出的限容量多旅行商問題模型比傳統多旅行商問題更具有實踐意義與價值。