不等厚磁極永磁電機解析法分析

倪有源,劉躍斌

(合肥工業大學,合肥 230009)

0 引 言

隨著我國“十三五”規劃的實施，高效、節能、經濟、持續等成為能源發展新方向。永磁電機具有結構簡單、體積小、功率密度高等優點，在艦船、航空、家電、醫療、公共生活等領域應用非常廣泛[1，2]。

在永磁電機運行過程中，永磁體起著重要的作用。永磁體的求解一般有磁化矢量法和等效面電流法，兩者出發點不同，但是得到的結果一樣。而且任何磁場都可以看成是由分布電流產生的，在永磁體被完全磁化的情況下，磁極內部的等效面電流密度可以認為是零，永磁體的求解也就是轉化為對磁極邊的等效電流求解。

文獻[3-5]分析了磁極內外弧圓心在同一點時，用等效面電流法求解徑向和平行充磁條件下的氣隙磁密分布。文獻[3，4]在平行充磁條件下，對磁極外弧圓心發生偏移的永磁電機氣隙磁密進行了等效面電流的分析求解，但是沒有求解感應電動勢和電磁轉矩等參數。文獻[6-9]運用磁化矢量法分析了磁極等厚的無刷永磁電機的開路場、電樞反應場以及負載場。文獻[10]進一步提出并分析了等厚磁極磁場徑向和平行磁化的改進模型。文獻[11]在考慮槽的影響時，采用子域模型求解電機性能。文獻[12]將磁極設置為等效的導體電流，然后將電機劃分為2類子區域，進行氣隙磁密和反電動勢的解析求解。

對于永磁體內弧偏心的情形，本文通過等效面電流法求解不等厚磁極無槽永磁電機的氣隙磁密，引入相對磁導函數，進一步求解有槽電機的氣隙磁密、反電動勢以及電磁轉矩等參數。最后通過有限元法的計算結果驗證了解析法的有效性，為電機在各種偏心情況下的參數計算提供了參考。

1 不等厚磁極永磁電機結構

從傳統瓦形磁極內外弧圓心在同一點結構出發，得出磁極內弧圓心和外弧圓心發生偏移的一種磁極結構。在已知不等厚磁極最大厚度、最小厚度以及永磁矯頑力等參數的條件下，通過改善氣隙磁密的分布來提高永磁電機的運行性能。傳統瓦形內外弧圓心在同一點，即等厚磁極結構如圖1所示。磁極內弧圓心偏移外弧圓心一定距離后，即不等厚磁極結構如圖2所示。

圖1 等厚磁極永磁電機結構

圖2 不等厚磁極永磁電機結構

2 內弧偏心解析法求解

對于傳統無槽等厚磁極結構的電機氣隙磁密的求解，在文獻[6]中給出了完整的解析式。對于內弧偏心磁極結構，分別在徑向和平行2種磁化方式下，采用等效面電流法將磁極等效求解氣隙磁密表達式。

2.1 徑向充磁下的氣隙磁密解析法求解

在圖2的磁極內弧偏心結構中，R1為以O點為圓心的外弧半徑，內弧偏心后磁極最小厚度為hmin，最大厚度為hmax。

圖3 徑向充磁磁極等效面電流

由圖2可見，OA=R1-hmin，O′A=R1-hmax+h，OO′=h。

在△OO′A中，根據余弦定理可得：

式中：αp為永磁體極弧系數；p為極對數。

永磁體的AD邊和BC邊的圓心距h：

在AD邊，任意一點E到O點的距離：

AD邊的等效面電流微元：

式中：

于是，該電流微元在氣隙中產生的磁密：

式中：μ0為真空磁導率；Rs為定子內半徑；θ為定子內表面上一點到磁極中心線的機械角度。

由以上各式通過積分，可得AD邊的磁密：

(7)

式中：α是永磁體AB邊到磁極中心線的機械角度。

而AB邊和CD邊的等效面電流微元：

di=Hcdr

(8)

根據等效面電流微元，可以求解在氣隙中所產生的磁密：

對式(9)積分得到在定子內表面的磁密：

式中：

然后將AD邊、AB邊和CD邊的氣隙磁密疊加，得到每極的等效面電流法氣隙磁密解析式。在一個周期內，對每極求解的結果進行疊加，就可以得到氣隙磁密的分布。

2.2 平行充磁下的氣隙磁密解析法求解

在已知條件不變的情況下，采用平行充磁時，如圖4所示的磁極等效面電流可知，AB邊和CD邊的等效面電流方向相反，大小相同，而且面電流密度大小：

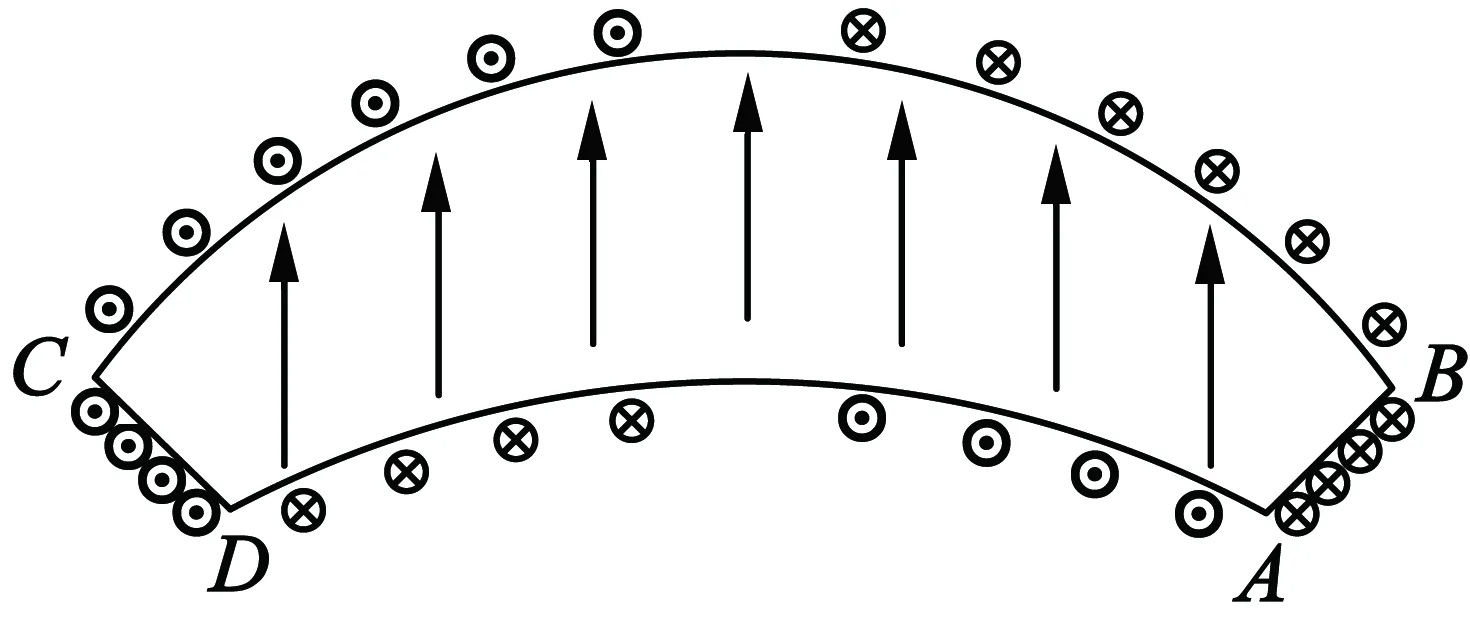
圖4 平行充磁磁極等效面電流

BC邊的等效面電流密度大小：

J2=Hcsinθ0(13)

AD邊的等效面電流密度大小：

AB邊和CD邊的面電流產生的氣隙磁密：

BC邊的等效面電流微元：

di=Hc·sinθ0·R1·dθ0(16)

該電流微元在氣隙中產生的磁密：

由以上關系式數值積分可以得到BC邊磁密：

曲邊AD的等效面電流微元：

其中：

那么該電流微元在氣隙中產生的磁密：

由以上關系式積分，可以得到AD邊的磁密：

式(15)和式(21)中：α和θ的含義與徑向充磁的含義相同。

將AB邊、CD邊、BC邊以及AD邊求解的氣隙磁密疊加，就可以得到平行充磁下的一個磁極氣隙磁密解析式。

2.3 有槽結構電機的解析法分析

當求解有槽結構的電機性能時，由于有槽結構的子域解析求解比較復雜。因此在誤差允許的條件下，通過引入相對磁導函數求解該電機的氣隙磁密，并進一步獲得感應電動勢以及電磁轉矩等參數的解析式。

對于有槽結構的永磁電機，相對磁導函數由文獻[8]得出：

式中：b0為槽寬；α0=b0/Rs為槽寬對應的角度；αt=2π/Qs為槽距角；Qs為定子槽數；g′=g+hm/μr為有效氣隙長度；hm為相對偏移角度對應的磁極厚度。當永磁電機為內轉子結構時，即y=r-Rs+g′時，ν可以通過式(25)進行求解。

由式(23)～式(25)可以得到相對磁導函數的表達式：

將式(26)寫成傅里葉形式：

有槽結構永磁電機氣隙磁密的2個分量如下：

對于有槽結構的永磁電機，采用解析法求解反電動勢時，空載徑向氣隙磁密：

式中：θma為取決于轉速的相對位置角，表達式：

θma=ωrt+θ1(30)

式中：ωr為轉子的機械角速度；θ1為轉子的初始位置角。

由單個線圈的磁通，可獲得各相繞組的感應電動勢：

式中：N為每相總串聯匝數；L為定子鐵心長度；αc為線圈的節距角；Kdn=sin(npαc/2)為繞組的節距因數；Kqn為繞組的分布因數。

電機電磁轉矩為感應電動勢和電流的乘積，即：

式中：ei和ii(i=a，b，c)分別為定子三相繞組的感應電動勢和電流。

對于定子電流，各相基波表達式分別如下：

式中：Im為每相電流的最大值；φ為相位角。

3 內弧偏心磁極電機性能分析

采用等效面電流解析法求解永磁電機氣隙磁密，具有用時短、參數易優化等優點。本文對一臺3相4極、采用徑向充磁的永磁電機進行分析。電機額定轉速為3 000 r/min。表1列出了該電機的主要參數。

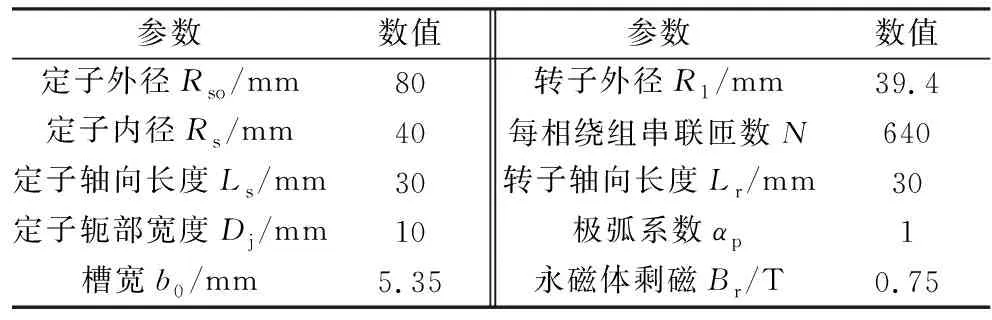
表1 永磁電機參數

根據表1中的參數，首先通過文獻[6]中的解析表達式，得到無槽等厚磁極永磁電機的氣隙磁密分布。磁極厚度設置為5 mm。圖5是徑向充磁下的內外弧圓心在同一點的徑向氣隙磁密波形，圖6是切向氣隙磁密波形，與有限元法的結果完全吻合。

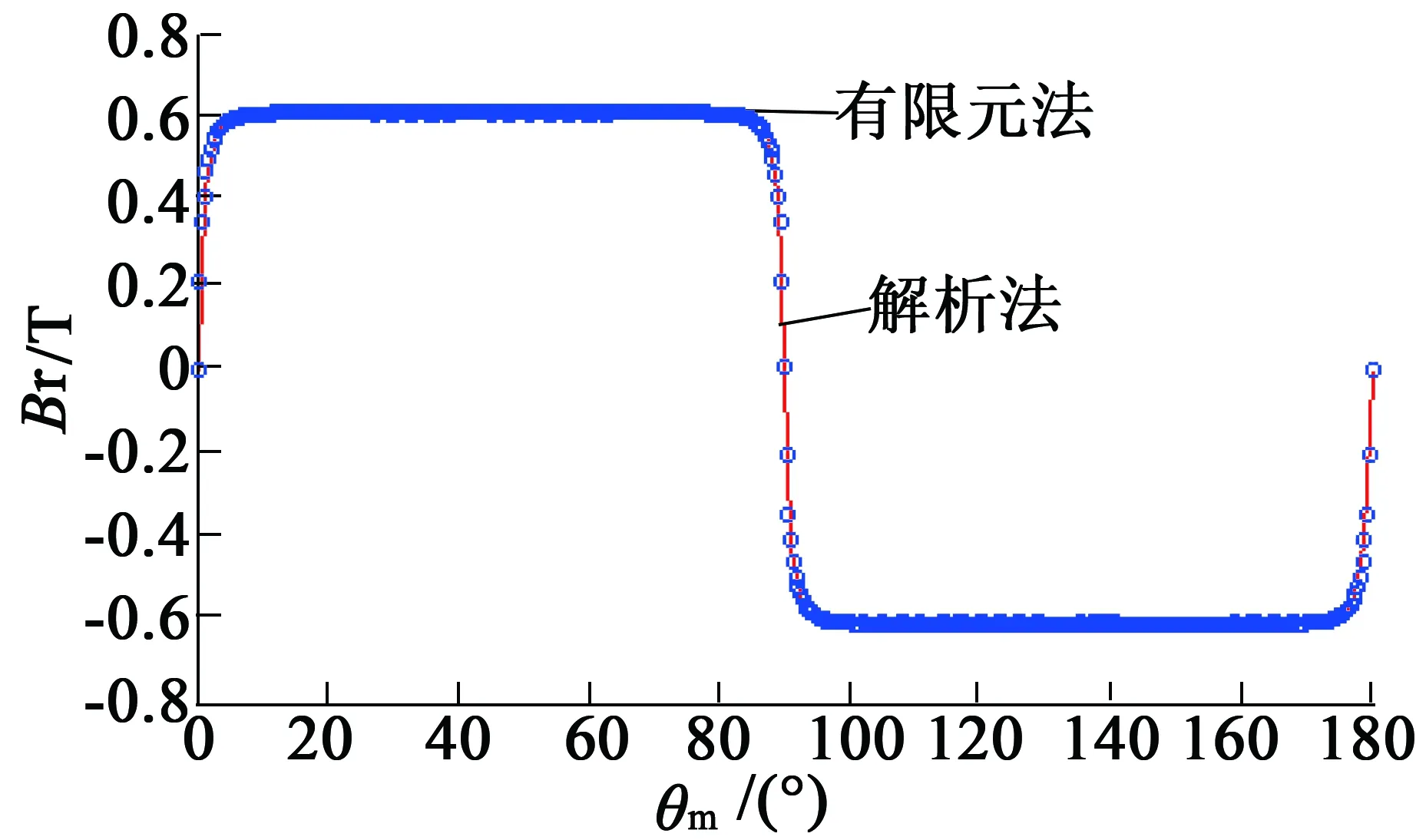
圖5 無槽等厚磁極電機徑向氣隙磁密波形

圖6 無槽等厚磁極電機切向氣隙磁密波形

接著分析磁極內弧圓心偏移情況下的氣隙磁密。在最大磁極厚度和最小磁極厚度為定值的情況下，改變最大磁極和最小磁極的數值，然后求解得到不同的偏心距離，再通過等效面電流法得到不同的偏心距下的氣隙磁密、電磁轉矩等參數。表2列出的是在徑向充磁下，最大磁極厚度和最小磁極厚度發生變化時，2種方法計算得出的電磁轉矩平均值。

表2 不等厚偏心磁極的電磁轉矩平均值

根據表2中的數據，選擇最后一組數據，求解該電機在不同偏心距下的各種性能參數。徑向充磁下，最大磁極厚度6.1 mm，最小磁極厚度3.9 mm。磁力線的分布可以精確反映電機內部的磁場強弱。在有限元計算中，獲得的電機磁力線分布如圖7所示。

圖7 徑向充磁電機磁力線分布圖

對于有槽結構的電機，通過相對磁導函數求解氣隙磁密。由式(23)～式(27)得到在定子內徑處的相對磁導函數波形，如圖8所示。

圖8 定子內徑處相對磁導波形

得到相對磁導函數后，由式(28)可以求出不等厚磁極有槽電機的徑向氣隙磁密，波形如圖9所示。

然后對氣隙磁密波形進行FFT諧波分析，可以得出徑向氣隙磁密的基波和諧波，如圖10所示，其中基波幅值為0.686 T。

圖9 電機徑向氣隙磁密波形

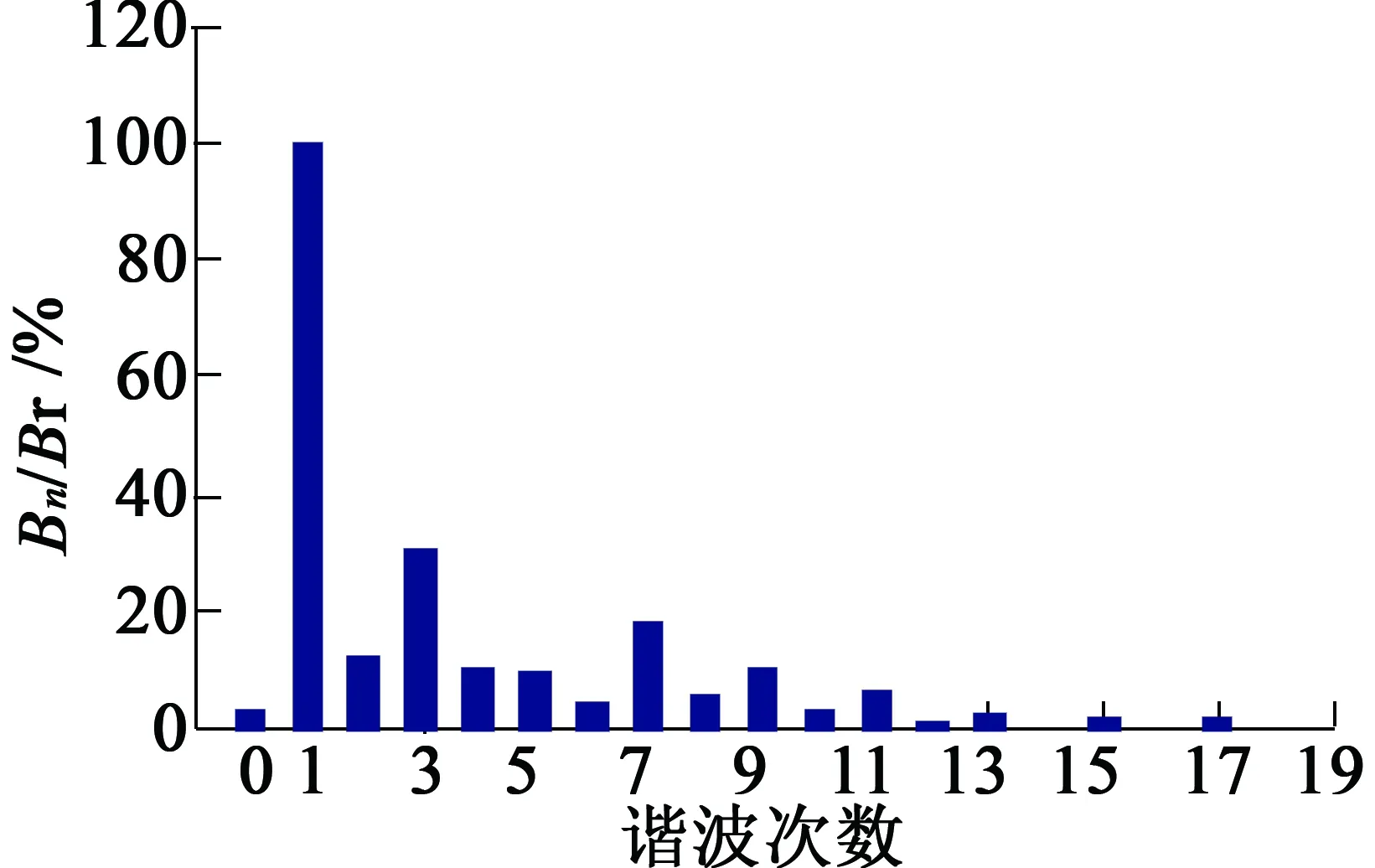
圖10 電機徑向氣隙磁密FFT諧波分析

反電動勢是電機性能分析的重要參數之一，反電動勢與轉子角速度、永磁產生的磁場、繞組匝數以及繞組分布有關。解析法和有限元法計算獲得的a相感應電動勢的波形如圖11所示。由于實際槽深以及假設條件等多因素的影響，2種方法得到的波形存在誤差，但整體一致性較好。

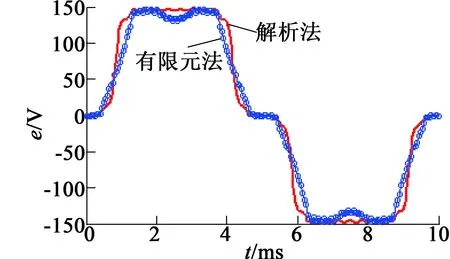
圖11 電機的相感應電動勢波形

電磁轉矩也是電機的重要參數之一。電磁轉矩不僅反映了電機的輸出能力，而且電磁轉矩脈動可以用來分析電機的振動和噪聲，對電機的性能分析起著至關重要的作用。由式(32)獲得的電磁轉矩波形如圖12所示。

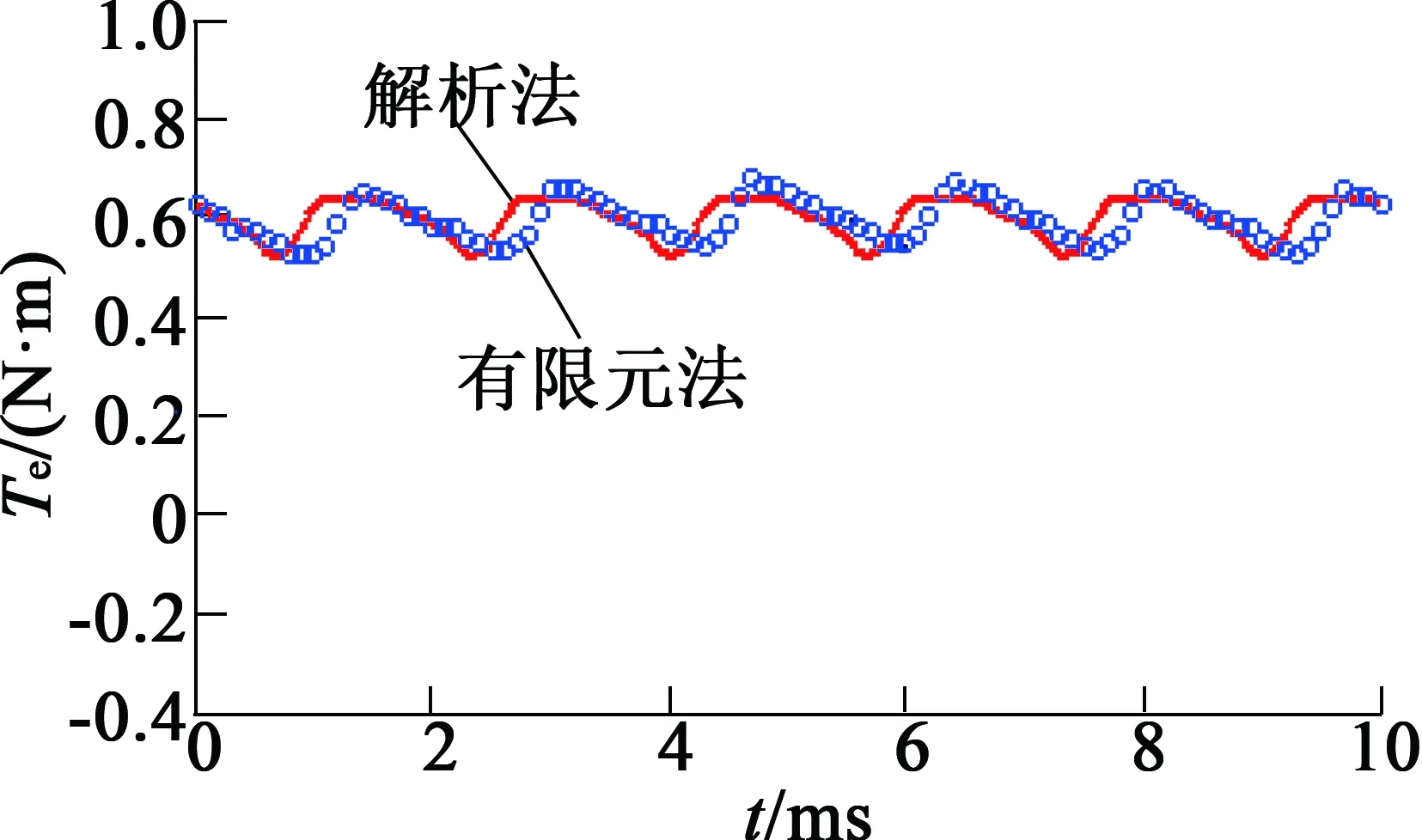
圖12 電機的電磁轉矩波形

解析法獲得的平均電磁轉矩為0.591 2 N·m，有限元法獲得的平均電磁轉矩為0.592 8 N·m。二者的誤差較小，從而驗證了磁極等效面電流解析法的正確性。

4 結 語

本文采用磁極等效面電流的解析法，計算了內弧圓心偏移下的永磁電機電磁性能。通過此方法求解無槽結構永磁電機在不同磁化方式下的氣隙磁密，通過引入相對磁導函數求解有槽電機的氣隙磁密，進一步求解有槽結構電機的反電動勢以及電磁轉矩等參數。最后通過有限元法驗證了解析法的正確性。結果表明，通過改變永磁磁極最大厚度和最小厚度，可以影響氣隙磁密和電磁轉矩等參數。本文的方法對電機各種偏心情況下的參數計算和優化設計提供了理論依據。