基于改進型擾動觀測器的IPMSM無傳感器控制

周 靜，楊振強，王繼超

(1.大連理工大學，大連 116024；2.中國人民解放軍31696部隊，錦州 121017)

0 引 言

無位置傳感器技術，可以通過建立合理的數學模型，替代傳統的機械式編碼器，獲得電機的位置信息。由于此技術能降低系統成本，減小電機體積，降低運行環境要求，因此具有較高的研究價值[1-3]。

對比表貼式永磁同步電機(以下簡稱SPMSM)，內置式永磁同步電機(以下簡稱IPMSM)是嵌入式轉子結構，具有可靠性強、調速范圍大、效率高等優點，是目前發展的主流[4-6]。但是，IPMSM存在凸極效應，磁路非線性，電機數學模型相對復雜，在無位置傳感器技術中，用于轉子位置信息估計的觀測器設計與調試過程相對復雜，不易于工程實現[7，8]，本文致力于解決此類問題。

近年來，隨著科研工作者對無位置傳感器技術研究的深入，取得了大量的研究成果。文獻[9]提出了一種基于合成反電動勢的滑模狀態觀測器，實現了IPMSM無位置傳感器控制系統的高速穩態運行，但是在開關切換時容易引入高頻信號，需要通過兩級濾波器對其進行消除，調試起來復雜。文獻[10]基于非線性觀測器實現了IPMSM無位置傳感器控制，轉子位置與轉速估算精度高，缺點是設計過程復雜、計算量大，且計算過程中需要借助狀態的微分，導致噪聲信號的放大，因此采用了低通濾波器，調節過程較復雜。文獻[11]在一種新型的擾動觀測器的基礎上實現了SPMSM無位置傳感器控制。其設計過程簡單，結果精確，調試過程簡單，容易應用。但是，其觀測模型是基于SPMSM的電流狀態方程搭建，因此不適用于IPMSM。

本文結合多種控制策略的優點，研究了一種基于改進型擾動觀測器的IPMSM控制方法。此方法通過合成反電動勢，得到與SPMSM相似的模型，再利用中間變量轉換，在不添加濾波器的條件下求得理想的合成反電動勢，將其與鎖相環結合得到轉子位置信息。利用一個隨轉速變化的誤差補償環節，消除了因為模型誤差導致的轉子位置估算誤差。通過對仿真結果分析，此方法調試過程簡單，能夠精確地估計轉子位置信息，從而完成高性能的IPMSM無位置傳感器控制。

1 IPMSM數學模型

在靜止α，β坐標下，IPMSM的電壓方程如下：

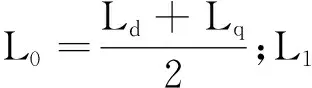
可以將式(1)改寫為矢量形式：

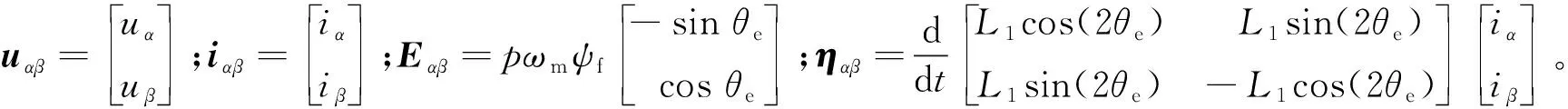
可以看出，因為IPMSM 的Ld,Lq不等，半差電感不為零，附加電壓ηαβ受θe的影響，導致利用反電動勢搭建觀測器的無傳感器技術不適用于IPMSM。因而，本文通過定義合成反電動勢，使IPMSM的數學模型變成與SPMSM 相似的模型。

通過坐標變換理論，對附加電壓ηαβ變換，可得：

式中:id為直軸電流。

通過將附加電壓ηαβ分解成E1，E2，E3，由式(2)和式(3)可知，E2與反電動勢Eαβ的相位相同，可以將其合并。

定義合成反電動勢Esyn:

E3與反電動勢Eαβ正交，而且和合成反電動勢的相比，E3的幅值比較小，為了簡化計算，可以將其忽略。

定義合成后的輸入電壓矢量vαβ：

將合成后的量代入式(1)，IPMSM 在α，β坐標系下的電壓方程可以變形:

從而，得到以定子電流為狀態變量的電機電流狀態方程:

2 擾動觀測器的設計

2.1 擾動觀測器的數學模型

干擾下的時域微分方程：

式中：x是狀態變量，u是輸入量，d是擾動量；A,Bu及Bd分別是與x,u及d對應的系數矩陣。

在干擾信號d變化遲緩的情況下，d的導數約等于0，可以忽略。

估計誤差：

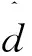
對應的擾動觀測器可以表示：

式中：L為擾動觀測器的增益矩陣。

本文采用了文獻[11]中利用中間變量轉換的改進型擾動觀測器，代入式(10)，可以得到：

定義中間變量：

從而，得到擾動觀測器的模型：

由于借助中間變量z，擾動量的估計不用計算狀態變量微分，所以不用額外設計濾波器對噪聲信號進行消除，從而簡化了觀測器。

本文將靜止α-β坐標下合成反電動勢Esyn作為擾動量，建立基于合成反電動勢的擾動觀測器模型。

對式(7)的IPMSM電流狀態方程整理可得：

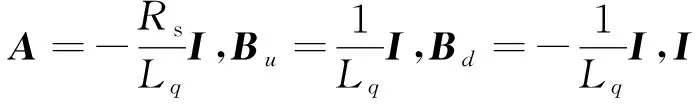
從而，得到基于合成反電動勢的觀測器模型：

式中：l為擾動觀測器的增益。

根據式(15)，作出的擾動觀測器結構圖如圖1虛線框所示。

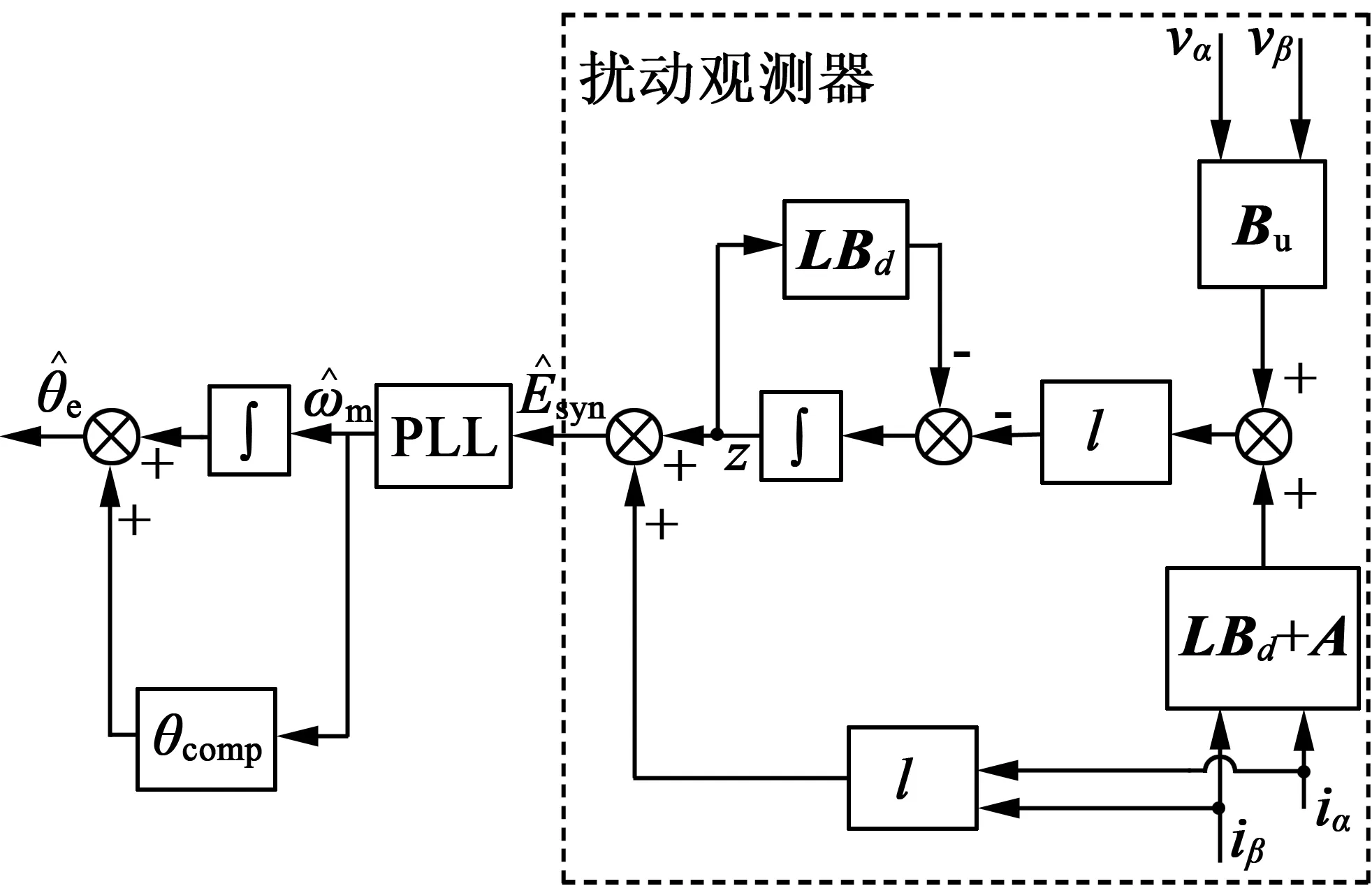
圖1 基于擾動觀測器的轉子位置估計

由圖1可知，定子電壓和電流經過改進型擾動觀測器可以估計出合成反電動勢。由于合成反電動勢中有IPMSM轉子位置和速度信息，結合PLL與對應的位置補償后可以實現對轉子位置和速度較為精確地估計[12-14]。

根據式(4)可以推出:

式中：k=pωm(ψf+2L1id)。

合成反電動勢利用PLL實現對轉子速度的估計，估計出的速度量再通過積分便能夠求得轉子位置。

2.2 轉子位置補償

為了消除因為觀測器模型誤差導致的轉子位置估算誤差，需要進行轉子位置補償。

對式(10)作拉氏變換，推導出擾動觀測器的傳遞函數：

因此，擾動觀測器可等效為一階慣性環節。

結合式(4)推出估計值：

得到轉子位置補償公式：

2.3 李雅普諾夫穩定性

擾動觀測器的動態誤差方程可以表示：

為了使速度估計誤差能夠收斂，定義式(22)李雅普諾夫函數。

對其求導：

l<0

3 仿真分析

本文采用型號為GK6080-6AC31的IPMSM，表1給出了IPMSM相關參數，圖2為IPMSM控制系統的結構框圖。

表1 IPMSM主要參數

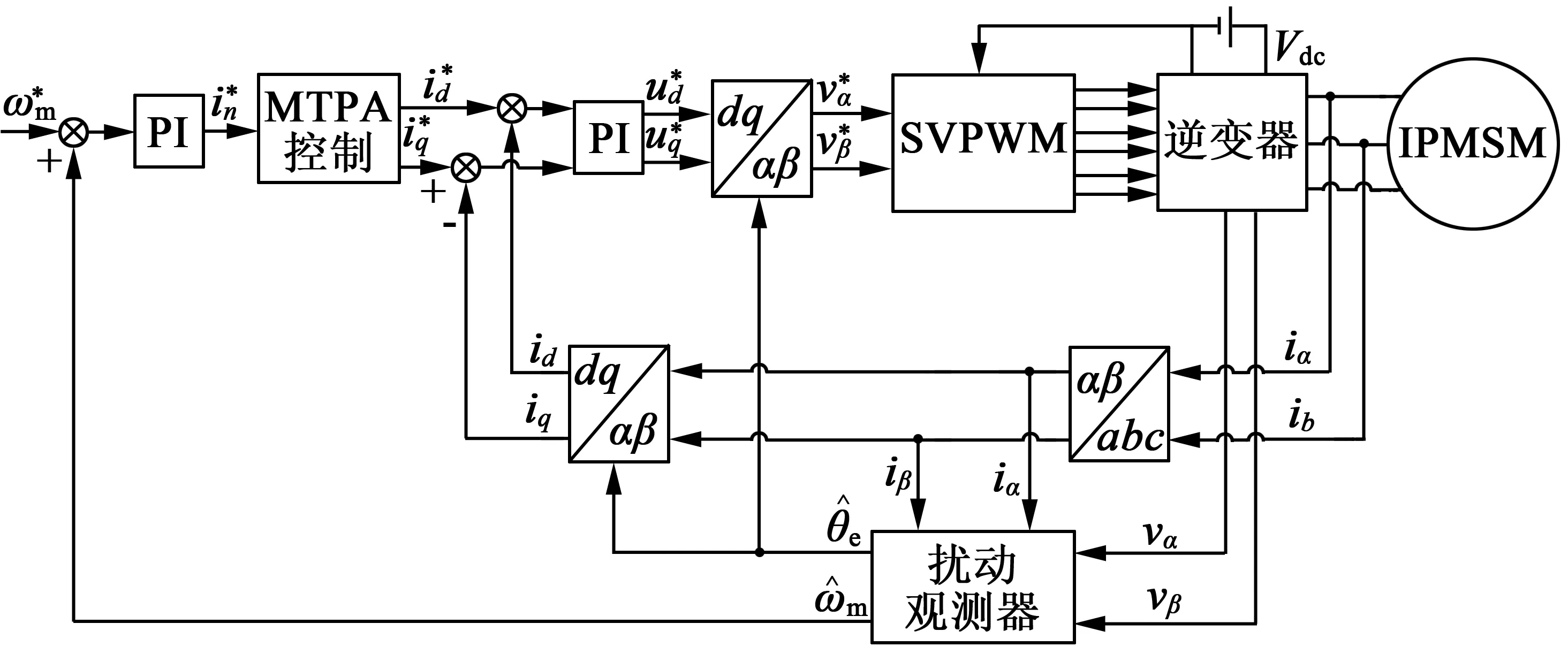
圖2 基于改進型擾動觀測器的IPMSM無位置傳感器控制系統結構框圖

在MATLAB/Simulink平臺上設計了系統的仿真模型，通過對基于改進型擾動觀測器的IPMSM無位置傳感器控制系統實行仿真，確定觀測器增益，驗證了觀測器對轉子信息的估計性能。

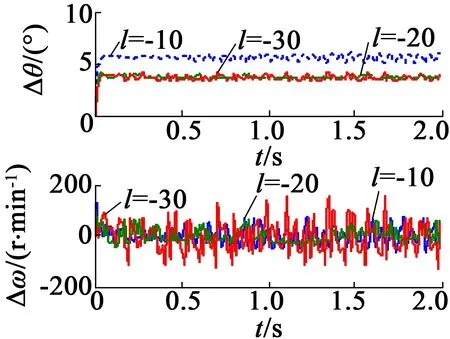
圖3 不同增益下的轉子誤差

由此可知，增益越小，轉子位置估計誤差越小，但是轉速誤差波動越大。為獲得較好的控制性能，系統選取的增益為-20。此增益選取方便，且產生的誤差在系統允許誤差范圍內，滿足系統要求。

選定增益后，討論負載變化對系統的影響。在1 s時，突加負載轉矩TL，TL的值分別取2 N·m，5 N·m，10 N·m。圖4是負載變化對轉速和位置誤差的影響。由圖4(a)可知，TL越大，轉子速度下降的幅度越多，但仍能實現對給定轉速的跟隨。由圖4(b)可知，TL越大，轉子位置誤差略有增加，轉子位置誤差最大不超過8°電角度。由此可知，觀測器具有較強的魯棒性。

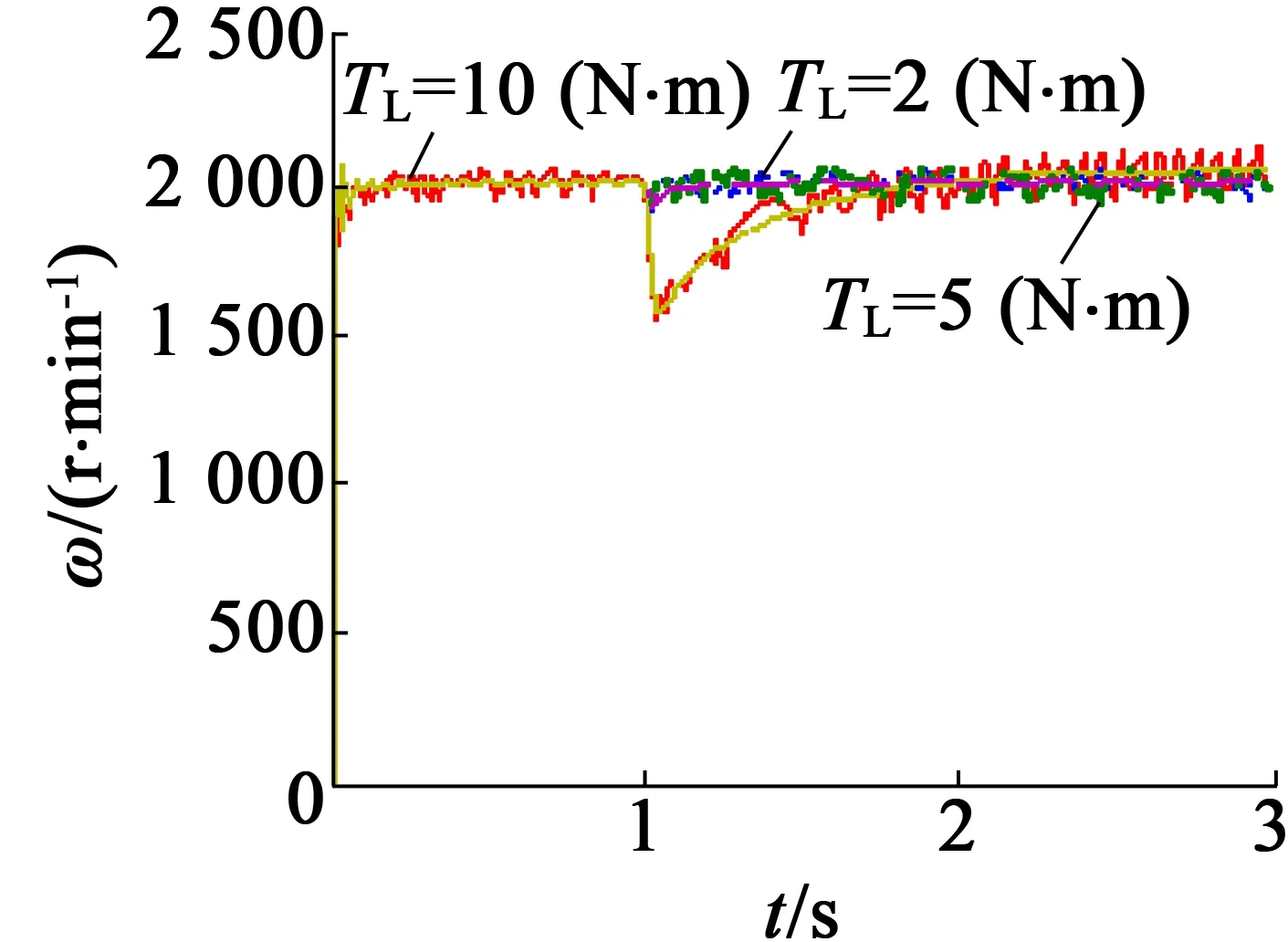
(a) 電機轉速

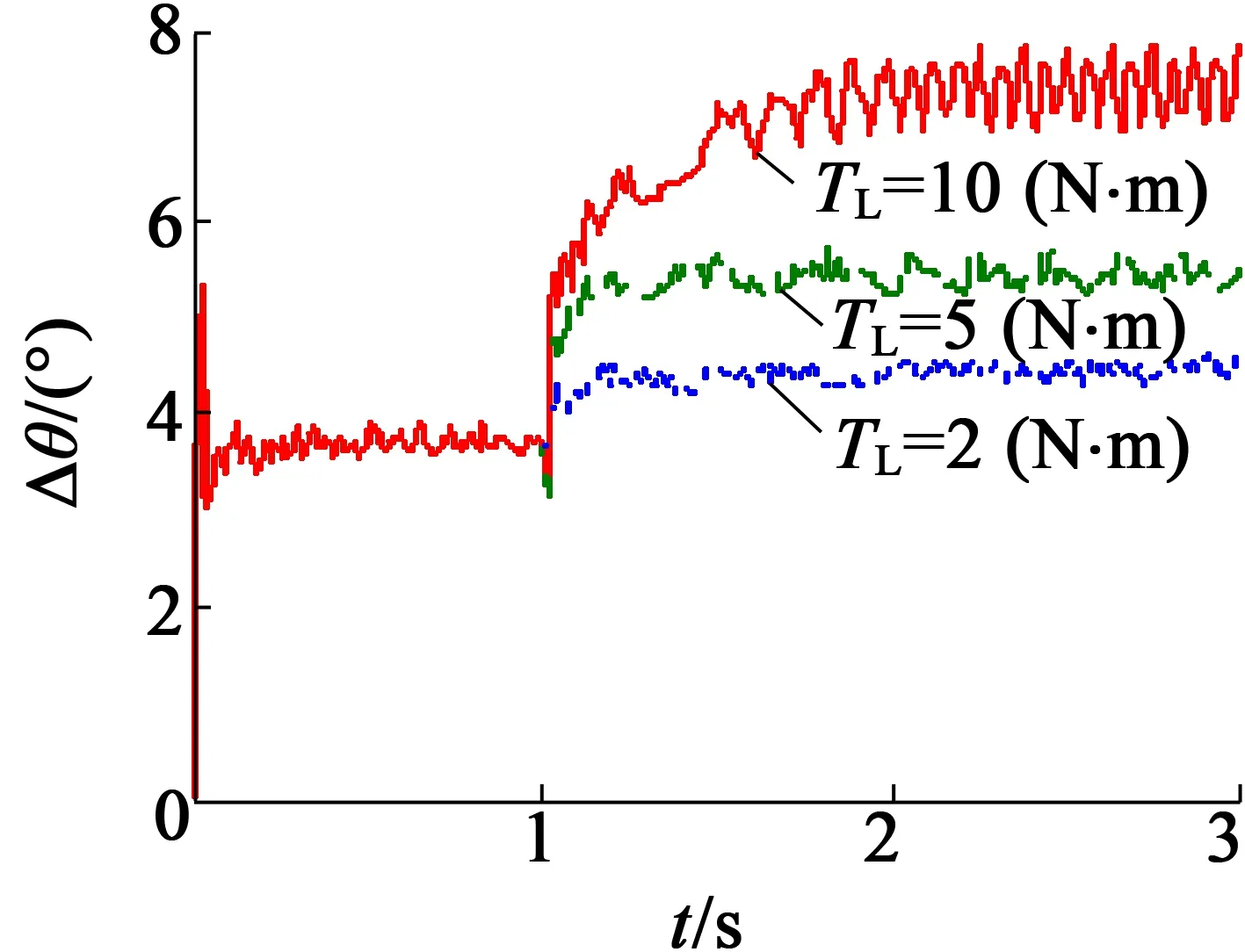
(b) 電機位置誤差

系統仿真時間設為4 s，IPMSM穩態運行在TL=2 N·m條件下，在2 s時，將電機給定轉速由500 r/min階躍到2 000 r/min，系統波形如圖5所示。從圖5可以看出，估計轉速能夠對實際轉速進行良好的跟隨。在給定轉速500 r/min 的情況下，轉子的速度誤差約±15 r/min，速度誤差波動近似為3%。在給定轉速2 000 r/min 的情況下，轉子的速度誤差近似為±50 r/min，速度誤差波動約為2.5%，速度誤差波動稍微有所減小，轉子位置估計誤差近似為4.6°電角度。

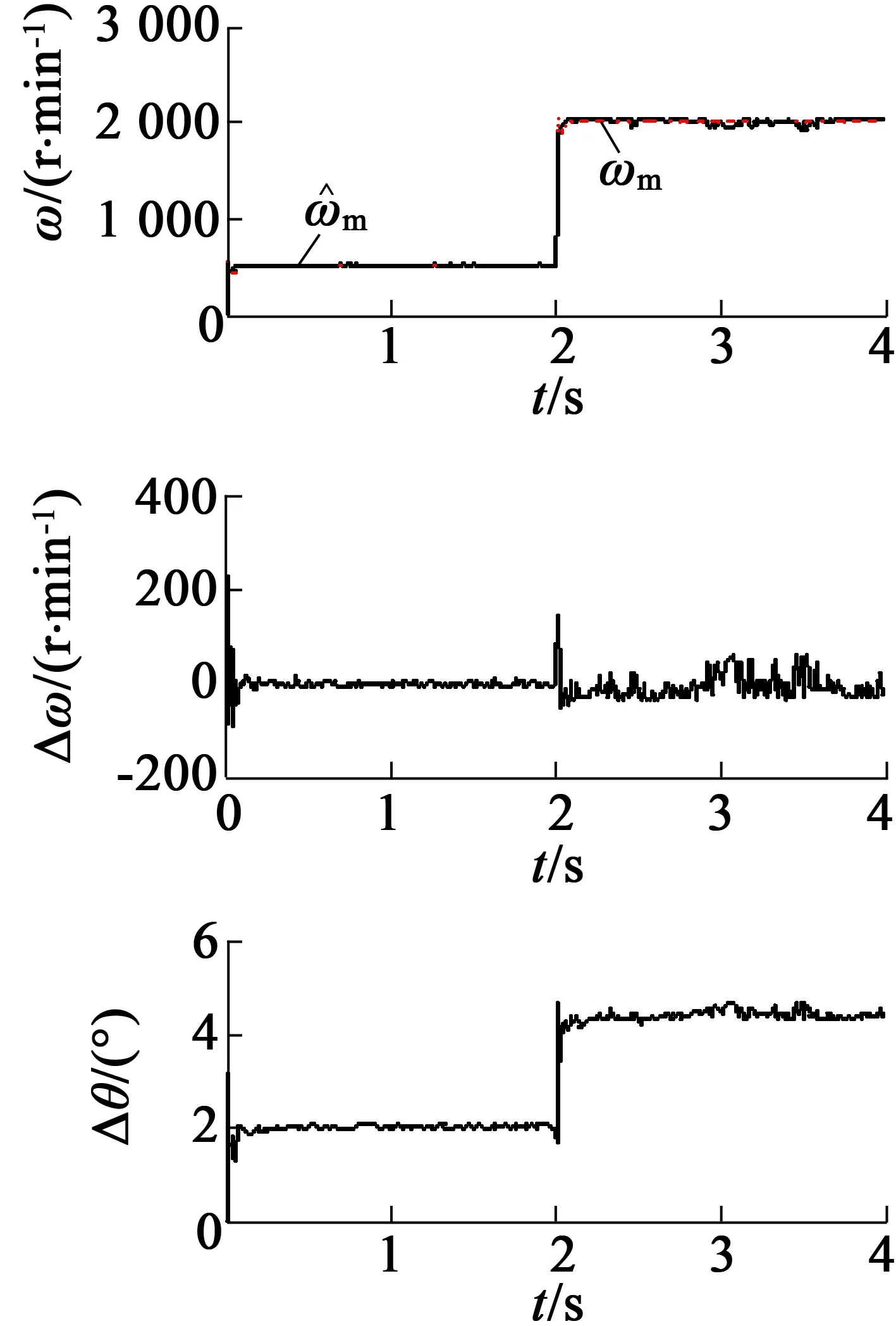
圖5 轉速階躍變化時系統波形

為了進一步驗證電機控制系統的性能，在1 s時，將IPMSM的轉子速度在200 ms內，從500 r/min斜坡上升到2 000 r/min，運行后，再用同樣的速率，降到500 r/min，系統波形如圖6所示。

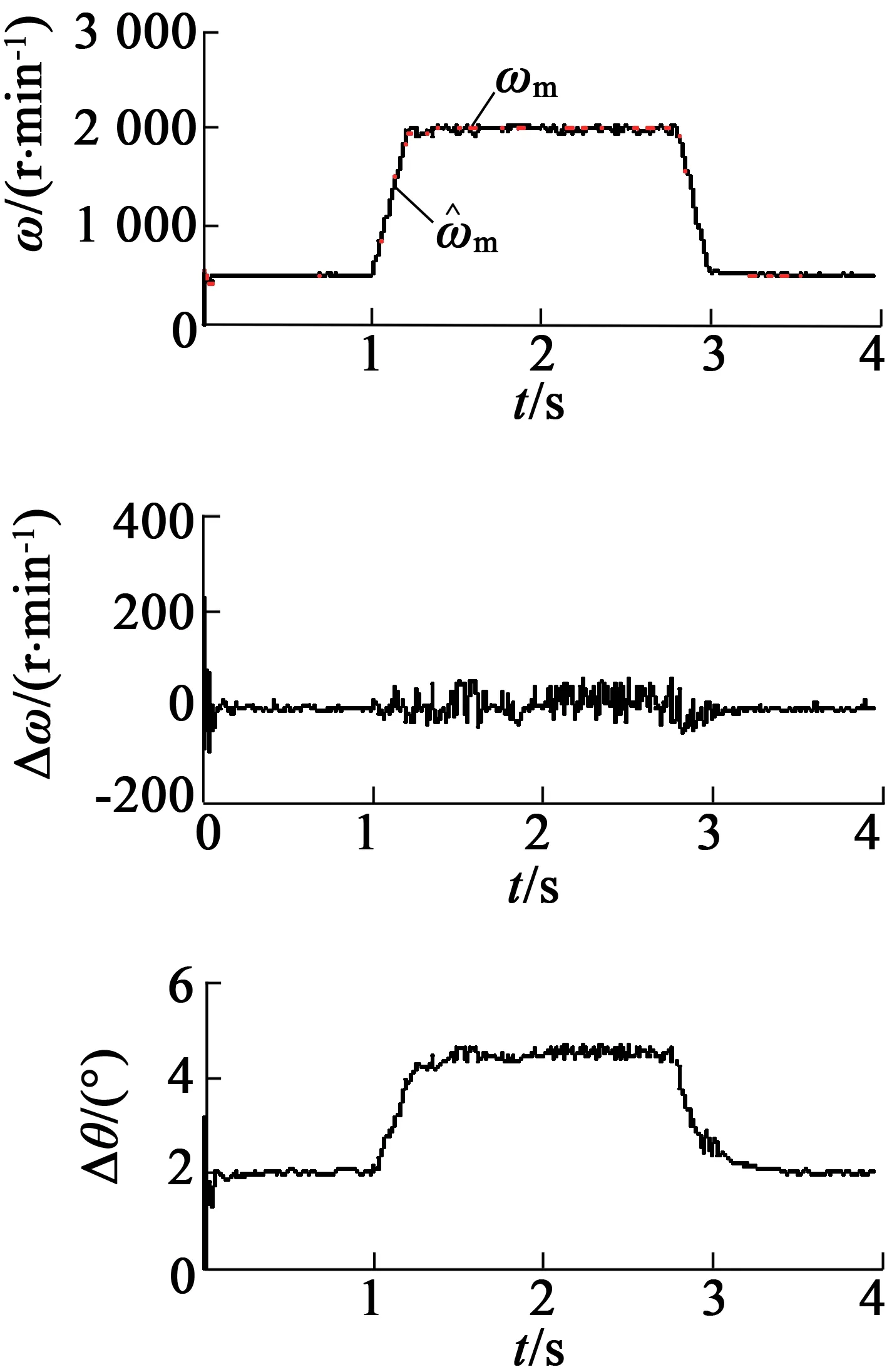
圖6 轉速斜坡變化時系統波形

從圖6可以看出，在加減速過程中，估計轉速同樣能夠對實際轉速進行良好的跟隨，轉子速度動態誤差小于50 r/min，靜態誤差小于15 r/min，始終不超過給定轉速的3%，轉子位置誤差始終不超過4.6°電角度。

對比文獻[9]和文獻[10]中的觀測器，此觀測器設計相對簡單，雖然轉速誤差波動略有增加，但是精度滿足系統要求。

綜上所述，此擾動觀測器能夠準確地估算轉子位置和轉速，實現了IPMSM高性能的運轉。

4 結 語

本文基于改進型擾動觀測器建立了IPMSM數學模型，將合成反電動勢作為擾動量，利用中間變量，結合鎖相環對轉子位置和轉速進行估算，實現了高性能的IPMSM無位置傳感器控制。通過仿真分析了不同觀測器增益和負載轉矩對轉子誤差的影響，選擇了合適的增益，完成了仿真驗證，得到以下結論：

1) 改進型的擾動觀測器利用中間變量，不用設計額外的濾波器，就可以估算出合成反電動勢，模型設計與調試過程簡單，易于工程實現，具有較高的應用價值。

2) 估算精度較高，在不同負載下具有較強的魯棒性，可以在轉速階躍與斜坡變化時實現轉子位置和轉速的準確估算，擁有較高的動態與穩態性能。

3) 不足之處，此系統基于反電動勢估計，適用于IPMSM中高速調速，所以，還需進行低速研究。