初中函數概念的教學策略分析

□張蕓蕓

對很多初中生來說，函數概念較難理解和把握。筆者調查發現，大多數初中生的函數概念比較模糊，把握不了函數本質，甚至是曲解函數概念。函數概念難以掌握，除卻學生自身心理因素外，還由于函數是一個較抽象的辯證概念，而初中學生首次從常量數學引入變量數學，他們對 “變量”還不習慣；此外，函數類型眾多，表示方式多樣，沒有什么固定形式。初中教材中函數的表示方法有三種：解析式法、列表法、圖象法，但課本對列表法和圖象法介紹不多，初中生對這兩種表示方法的認知度不高，以至于不少學生理解的函數表達方式僅限于函數解析式，阻礙了他們對函數本質的認識。

因此，教師在函數概念教學時需要適度淡化概念的形式定義，以生活實例導入，在比較、變化等聯系性活動中揭示函數的內涵，以幫助學生理解函數概念的本質。具體來說，函數概念可由以下步驟呈現：

一、聯系生活實例引入函數概念

弗賴登塔爾曾指出，“運用實際生活中出現的函數概念，而不必先去生造或定義函數。只有學生能夠做出函數以后，再讓他去歸結出什么是函數，這才是數學活動的范例。”簡言之，數學概念的教學要遵循學生的一般認知規律，從表象到規定，從具體到抽象。函數知識在社會生產、生活和科技中廣泛應用，例子不勝枚舉。在函數教學中，教師要從實際出發，通過與概念有明顯聯系的實例，使學生在對具體問題的體驗中感知函數。比如，在超市買蘋果，蘋果單價是6.5元/斤，買x斤的蘋果與需要支付的錢m之間的關系是什么？坐出租車，車費會隨著路程的遠近而不同，等等。這些實例易于理解，且易激發學生學習函數的興趣，還讓學生體會到函數是 “好用的數學”。教師充分利用學生熟悉的實例來引入函數學習，既是滲透函數思想方法的捷徑，也有助于實現函數 “概念性的數學化”。

二、運用變式材料和否定例證來明確函數本質

首先，根據對一定數量感性材料的觀察、分析，提煉出感性材料的共同屬性，給出函數概念的定義。對初中函數概念的理解，教師要引導學生抓住以下幾點：①在一個變化過程中；②兩個變量中一個變量的數值隨著另一變量數值的變化而變化；③對每一確定的自變量值，因變量都有唯一值與其對應；④某一類型函數所具備的獨有的特征或關系。其次，為更鮮明地解釋函數概念本質，促使學生深化內涵認識，教師應給出一些函數的變式材料和否定例證。如在八年級上學期剛教給學生函數定義時，可引入以下例子幫助學生辨析函數本質：

（1）在彈性限度內，某彈簧的長度y與所掛物體的質量x滿足下表關系：

x（千克） 1 2 3 4 ……y（厘米） 3.5 4.0 4.5 5.0 ……

y是x的函數嗎？為什么？

（2）圖1是某地某月一天24小時中氣溫與時間的關系圖，該圖表述的是函數關系嗎？如果是，請說出自變量和因變量。

（3）圖2所示，該圖中y是x的函數嗎？為什么？

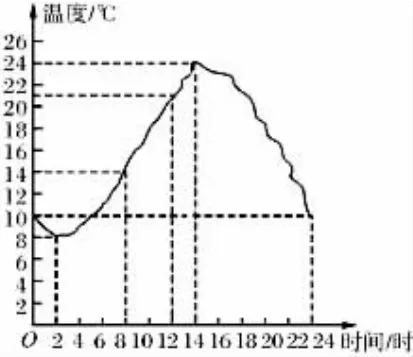
圖1

圖2

（4）關系式2x+y=5表述的是函數關系嗎？如果是，請說出自變量和因變量。如果不是，請說明理由。

通過這些肯定和否定例證的辨析，進一步促進學生對函數概念內涵的深化學習，了解函數的表達方式多樣，涉及的種類繁多。

三、借助新舊知識聯系加深對函數概念的理解

在八年級學習 “函數”這一內容之前， 《代數式》一章就已經讓學生體會到字母表示數的必要，同時要求學生能結合具體問題情境列出代數式，并根據數值的不同求取不同的代數式值，這已經滲透了初步的函數思想。同時，該章還通過找規律填圖表、“數值轉換機”模式等多種形式讓學生體會變量之間存在著對應關系。此外， 《平面直角坐標系》為與函數圖象有關的知識學習打下基礎。平面直角坐標系既是研究函數問題的有效工具，又是滲透數形結合思想、發展空間觀念的重要載體。而函數概念的學習又為后續函數圖象與性質、函數應用的學習打下基礎。每一種類型的函數學習都將使學生對函數概念的理解進一步加深，也使得函數概念體系結構顯性化。

在分別學習一次函數、反比例函數和二次函數的概念時，每一種函數概念也可與其他函數概念進行類比，以明確不同函數概念間的各種聯系，幫助學生建立有用的知識網絡結構圖。

當然，對于函數概念真正的認知和理解是不容易的，要經歷一個較長的多次接觸的過程。掌握函數概念的本質，絕不是背誦定義；對于函數概念定義的呈現，應以學生的可接受度為前提。教師在函數概念教學的過程中，要綜合考慮所教學生的知識儲備、心理水平及函數概念本身特性；對學生要有恰當的期望值，不可急于求成；鼓勵學生對新知識產生探究欲望，盡力促使學生對函數學習產生興趣和信心。

例如，反比例函數概念的教學根據以上策略可做如下設計：

11.1反比例函數

【教學目標】

1.理解反比例函數的概念，能結合具體情境理解反比例函數的意義；

2.能根據已知條件確定反比例函數關系式；

3.體會反比例函數是刻畫現實世界特定數量關系的一種數學模型；

4.感受數學來源于生活，應用于生活，讓學生樹立學好數學的自信心。

【教學重點】

理解反比例函數的概念，根據實際問題確定反比例函數關系式。

【教學難點】

理解反比例函數的概念。

【教學過程】

1．回顧舊知。提問：（1）在小學里，我們學過如果兩個量x、y滿足xy=k(k為常數，k≠0)，那么x、y就成什么關系？ （教師板演xy=k，其中k為常數，k≠0）

同學們能舉出生活中成反比例關系的具體實例嗎？ （教師可先舉例做示范）

（2）什么是函數？

一般地，設在一個變化的過程中有兩個變量x和y，如果對于變量x的每一個值，變量y都有唯一的值與它對應，我們稱______。其中，x是______，y是______。

我們已經學習過哪些類型的函數？它們的一般形式是怎樣的？

設計意圖：教師通過帶領學生復習反比例關系及已學相關函數知識，為后續學生自主探究和深刻理解反比例函數的概念打好基礎。

2．探索新知。

“想一想”

家住上海的姨媽邀請王明暑假去上海的迪士尼樂園游玩。王明計劃坐汽車從南京出發去往上海 （全程約300千米）。全程所用時間t（小時）隨汽車速度v（千米/小時）的變化而變化。

（1）你能用含v的代數式表示t嗎？

（2）利用 （1）的關系完成下表，并說說隨著時間的變化，全程所用的時間會發生怎樣的變化？

v（千米/小時） 60 70 80 90 100 t（小時）

（3）時間t是速度v的函數嗎？為什么？

（4）時間t是速度v的一次函數嗎？是正比例函數嗎？為什么？

設計意圖：利用學生生活中熟悉的實際情境引導他們應用反比例關系，初步感知反比例函數；認識到函數類型多樣，在生活中應用極廣。使學生易于接受新的概念，培養學生在生活中發現數學的能力。

“議一議”

（1）用函數關系式表示下列問題中兩個變量之間的關系：①游泳池的容積為5000立方米，向池內注水，注滿水所需時間t（h）隨注水速度v(立方米／h)的變化而變化；②某市電話的月租費是20元，每次打電話再付費0．6元。每月電話費y(元)隨通話次數x的變化而變化；③水滴激起的波紋不斷向外擴展，擴大的圓的周長C隨著r的變化而變化；④某村有耕地面積200畝，人均占有耕地面積y(畝)隨人口數量x(人)的變化而變化；⑤實數m與n的積為－200，m隨n的變化而變化。

（2）提問：以上函數關系式中哪些是已經學過的？剩下的函數關系式具有什么共同特點？你還能舉出類似的實例嗎？你能結合兩個變量之間的關系給這些新函數命名嗎？

（3）討論：什么是反比例函數？

（4）總結：一般地，形如y=k／x（k為常數，k≠0）的函數稱為反比例函數，其中x是自變量，y是因變量，k是比例系數。

設計意圖：引導學生通過對以上這些不同于一次函數和正比例函數的函數關系式的共同特點進行梳理，類比于正比例關系與正比例函數的聯系，討論得出反比例函數的定義。這樣既鍛煉學生觀察、類比和歸納的能力，也增強了學生的主體意識，提升學生學習興趣。

手勢在人與人生活中早已產生了共鳴。比如一只手上的大拇指和食指彎曲成圓圈，其余三根手指稍微分開且伸直，就有“好”、“可以”等含義。在體育課教學中體現的更加明顯。

“做一做”

例1．下列關系式中的y是x的反比例函數嗎？如果是，比例系數k是多少？

總結：（1）形如 y=kx－1（k≠0）或 xy=k （k≠0）的關系式也表示反比例函數關系；

（2）反比例函數的自變量的取值范圍是不等于0的一切實數。

設計意圖：教師向學生提供反比例函數關系的各種變式材料及一些極易混淆的其他類型的函數關系式，讓學生去觀察、辨析，加深對反比例函數本質的理解，明確反比例函數概念的內涵和外延，幫助學生掌握正確、完整的反比例函數概念。

例2．一定質量的氧氣，它的密度ρ(千克／立方米)是它的體積v(立方米)的反比例函數，當v=10立方米， ρ=1．43 千克 ／立方米。

（1）求ρ與v的函數關系式；

（2）求當v=2立方米時氧氣的密度ρ。

設計意圖：引導學生結合具體情境感知反比例函數的意義，體驗從實際問題中抽象出反比例函數模型的過程。進一步讓學生感受函數中因變量隨自變量的改變而改變，體會反比例函數中蘊藏的動態變換過程。

“練一練”

（1）課本 125－126頁的練習 1、 2；

（2）若y=（k-2）xk2-5是反比例函數，求此反比例函數的關系式。

設計意圖：通過這段演練，一方面加深學生對反比例函數概念的理解，另一方面讓學生不斷體會反比例函數在解決實際問題中的重要作用。

3．拓展提升。（1）函數y=（m－1）x|m|－2， 當m=_____時，它是正比例函數；當m=_____時，它是反比例函數。

（2）已知y=y1+y2，y1是x的反比例函數，y2是x的正比例函數，當x=2時，y=－6；當x=1時，y=3。求y與x的函數關系式，并求當x=－4時，求y的值。

設計意圖：拓展題 （1）促使學生將正比例函數與反比例函數的解析式進行類比，幫助學生更好地理解兩種不同函數的聯系和區別。問題 （2）將兩種不同種類函數組合成新函數，既拓寬學生函數認知的視野，提升學生的解題能力和思考能力，也為高中后續相關知識的學習做好鋪墊。

4．歸納總結。什么是反比例函數？它的形式有哪些？

5．課后作業。 （1）課本習題 11．1 1、2； （2）《數學補充習題》 11．1

總之，函數概念的教學對學生數學能力的提升發揮著重要的作用，在具體的教學中，教師應根據學生學情，對教學策略進行適當調整，以激發學生興趣，最終達到提高數學教學效率的目的。