電動汽車對開坡道雙模耦合驅動控制

張利鵬 董闖闖 張 偉 龐詔文 張思龍 賈啟康

燕山大學車輛與能源學院，秦皇島，066004

0 引言

開發高性能的智能電動汽車已經成為汽車產業可持續發展的必然途徑。電動汽車按照其驅動輪的動力來源劃分，可以分為集中式驅動和分布式驅動兩種模式［1］。由于有傳統汽車成熟的驅動技術可以繼承，故大部分電動汽車都采用了集中式驅動模式，但此類電動汽車行駛在對開坡道上時，低附著系數路面一側驅動輪的地面附著力會大幅減小，使此側驅動輪產生明顯滑轉。由于差速器具備兩側驅動半軸等扭矩分配特性，故會同步減小附著較好一側車輪的驅動力，這將導致車輛通過性能明顯降低，甚至無法爬坡。針對傳統集中式驅動系統所開發的牽引力控制系統（traction control system，TCS）能有效改善汽車在對開路面上的通過性能［2］，但利用制動系統進行驅動控制會損耗車載能量且增加成本，不利于整車性能的提高。相對而言，分布式驅動電動汽車的各驅動輪輸出轉矩可以獨立控制，在對開坡道上能夠充分利用兩側路面的附著力，從而維持車輛正常行駛，通過性能要明顯優于集中式驅動車輛。

分布式驅動電動汽車具有整車的多維動力學控制功能，可以靈活實現驅動防滑、差動助力轉向、直接橫擺力矩控制以及防側翻控制，從而大幅改善車輛的機動性、通過性和操縱穩定性［3-7］，但分布式驅動系統難以匹配變速裝置，車輛的驅動能力完全取決于電機的工作特性，其動力性和經濟性都受到了限制。此外，分布式驅動電動汽車在復雜路面或驅動電機故障等惡劣工況下很難保證各輪驅動力矩達到理想值，嚴重降低行車安全［8］。

為解決上述問題，筆者所在課題組發明了一種既可實現集中式驅動又能實現分布式驅動且帶有兩擋自動變速功能的雙模耦合驅動系統。該系統可以充分利用兩種驅動模式的各自優點并避免不適用工況，從而大幅提高整車的動力學性能。本文使用該系統的雙模耦合驅動控制來提升電動汽車對開路面的通過性能，并利用臺架和實車試驗驗證了控制效果。

1 系統轉矩輸出特性與控制方案

1.1 系統特點

雙模耦合驅動系統構型見圖1。該系統通過控制兩側驅動電機的工作狀態及操縱同步器進行模式和擋位切換，可實現圖2所示的雙電機集中式驅動和分布式驅動模式。

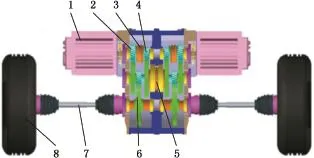
圖1 雙模耦合驅動系統構型Fig.1 Dual-mode coupling drive system configuration

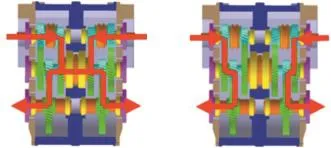
圖2 雙模耦合驅動系統的驅動模式Fig.2 Drive modes of the dual-mode coupling drive system

當車輛需要較高的加速和爬坡能力時，兩側驅動電機輸入軸與中間集中式驅動齒輪組的主動齒輪接合，進行雙電機集中式驅動；當車輛需要高速行駛時，兩側驅動電機輸入軸分別與各自相鄰的兩側分布式驅動齒輪組的主動齒輪接合，進行雙電機分布式驅動。該驅動系統具備兩擋自動變速功能，可以有效降低對電機性能的要求，能夠明顯改善車輛的動力性；可根據不同工況選取不同的驅動模式并協調兩側驅動電機轉矩輸出，有利于提高車輛的運行經濟性和行駛穩定性［9］。為了實現上述模式的切換控制，設計的變模執行機構見圖3，它由直流電機驅動一套蝸輪蝸桿機構轉動，蝸輪帶動一個雙向撥指左右擺動，再通過撥叉同步進行兩套同步器的變模換擋操作，從而通過機械互鎖避免兩側驅動模式不一致問題。

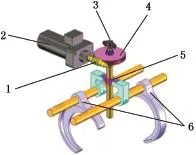
圖3 變模執行機構Fig.3 Modification of the implementing agencies

1.2 轉矩輸出特性

雙模耦合驅動系統集中式驅動模式兩側車輪的驅動轉矩輸出為

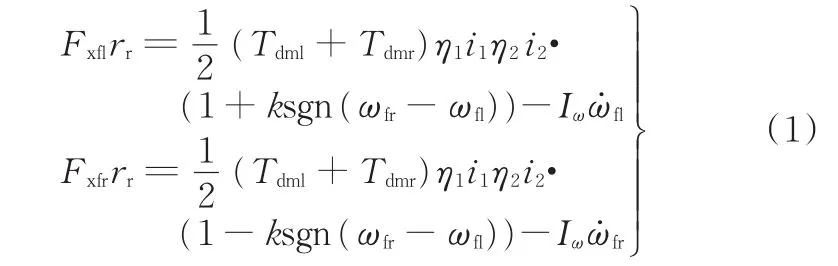
式中，Tdml、Tdmr分別為左、右兩側驅動電機的輸出轉矩；Iω為車輪的轉動慣量；Fxfl、Fxfr分別為左前、右前驅動輪的驅動力；rr為車輪半徑；ω?fl、ω?fr分別為左前、右前驅動輪的角加速度；k為差速器的鎖止系數；η1、i1分別為集中式驅動模式的一級減速器傳動效率和傳動比；η2、i2分別為二級減速器傳動效率和傳動比；sgn（）為符號函數。

雙模耦合驅動系統分布式驅動模式兩側車輪的驅動轉矩輸出為［10］

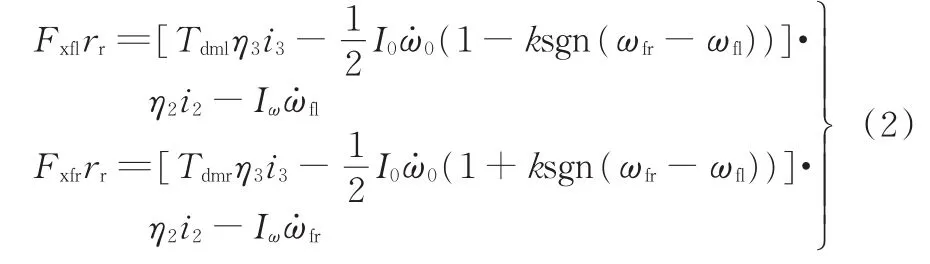
式中，I0、分別為中間一級減速器及差速器外殼組件的轉動慣量和角加速度；η3、i3分別為分布式驅動模式的傳動效率和傳動比。

從上述轉矩輸出特性分析可見，集中式驅動模式下，兩側驅動輪等轉速時，兩側驅動力矩完全相等，不等轉速時，高轉速側車輪驅動力矩小于低轉速側車輪，差值由總驅動力矩和差速器鎖止系數決定。該差值會對兩側驅動力矩分配產生一定影響，再加上差速器鎖止系數具有時變特性，故進行精確的車輪驅動力矩控制比較困難。分布式驅動模式下，兩側驅動輪等轉速時，兩側驅動力矩完全由驅動電機獨立控制；不等轉速時，中間一級減速器及差速器外殼組件的慣性力矩和差速器鎖止系數也會影響兩側驅動力矩的大小，但由于上述慣性力矩非常小，差速器鎖止系數可產生的力矩傳遞影響就更微小，因此，不等轉速時兩側驅動輪的驅動力矩也基本由驅動電機獨立控制，差速器的影響不用考慮，這為整車控制提供了便利條件。

1.3 雙模耦合驅動控制方案

雙模耦合驅動電動汽車在對開坡道上的變模控制系統架構見圖4。整車控制器（vehicle control unit，VCU）采集加速踏板開度信號、制動踏板開度信號、擋位信號等，用來分析當前駕駛員的駕駛意圖；同時，還要實時采集雙模耦合驅動系統兩側輸出軸的轉速，從而確定車輪相對滑轉率并判斷是否需要進行變模。整車控制器與驅動電機控制器以及變模電機控制器之間進行通信，實時發送控制信號。為保證動力性和低速驅動效率，車輛起步時優先采用雙電機集中式驅動模式，并根據效率最優原則分配兩側驅動電機力矩輸出。當整車控制器識別出需要變模時，首先，向驅動電機控制器發出自由模式請求，使驅動電機處于空轉狀態，驅動轉矩降為零；其次，進行集中式的摘擋控制，通過變模機構中的角位移傳感器進行撥叉實際位置的閉環控制；然后，當檢測到摘擋完成后，進行驅動電機轉速的主動調節，當轉速誤差滿足變模需求后，使驅動電機再次處于無轉矩輸出的空轉狀態；接著，進行分布式的進擋控制；最后，當角位移傳感器反饋信息顯示進擋完成后，驅動電機恢復正常的轉矩輸出，進行分布式驅動。由于針對分布式驅動的防滑控制已有大量研究成果，本課題組也開展過長期的理論與試驗研究［11］，故本文控制方案中不再涉及相關內容。

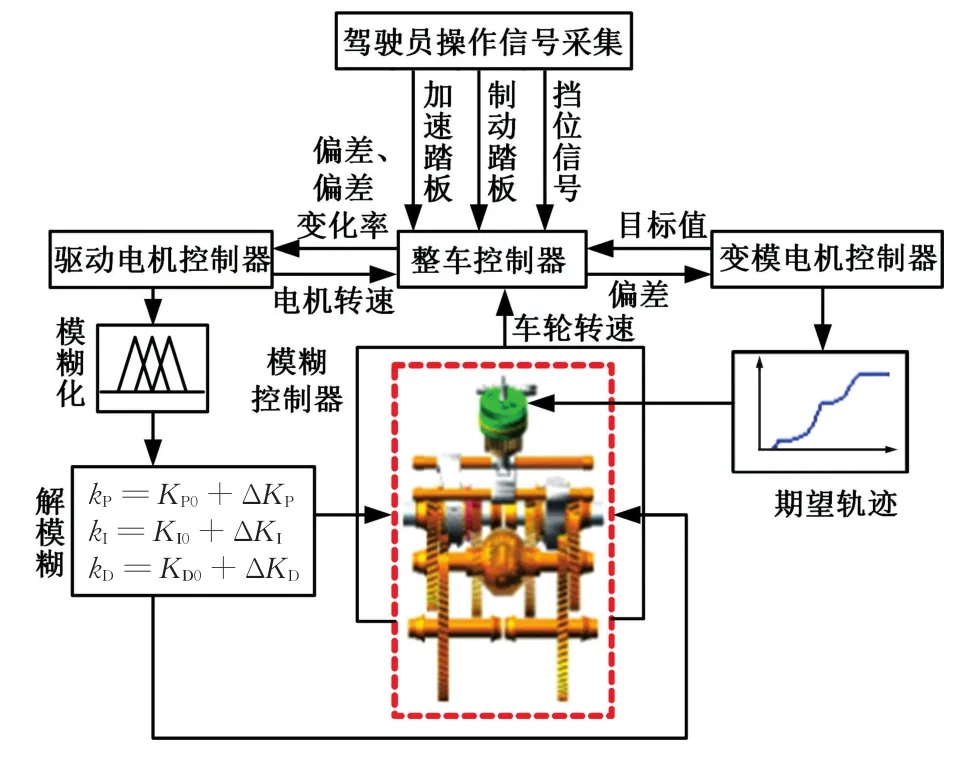
圖4 控制系統架構Fig.4 Control system architecture

2 控制器設計

2.1 變模觸發條件判定

對于對開坡道雙模耦合驅動系統變模的觸發條件判定，可以選擇驅動輪相對滑轉率門限值S*，當參考滑轉率S＞S*時，認為驅動輪已經發生滑轉，需要進行變模控制［12］。

研究對象為前輪驅動汽車，左前側驅動輪轉速為nfl，右前側驅動輪轉速為nfr。為了避免實際車速為零或抖動時對滑轉率辨識的影響，本文取二者平均轉速n0與車輪半徑的乘積為等效參考車速，即

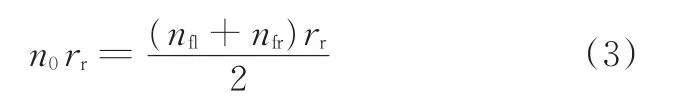
由于單側車輪滑轉出現時，該值會明顯大于實際車速，更有利于進行滑轉判定，因此，參考滑轉率

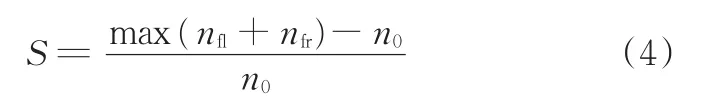
所得到的參考滑轉率會小于實際的車輪滑轉率，但由于對開坡道車速很低，車輪滑轉變化迅速，極短的時間內參考滑轉率即會達到較高值，故并不影響實際控制效果。驅動防滑的最佳滑轉率范圍通常為 0.05～0.20［13］，本文中選取相對滑轉率門限值S*=0.20，即當S＞0.20時開始進行變模控制。

2.2 驅動電機調速控制器設計

本文選取的集中式驅動模式和分布式驅動模式的總傳動比分別為 i1i2（i1i2=8.46）和 i3i2（i3i2=5.24）。由于存在轉速差且無離合器，故進行變模控制時需要進行驅動電機主動調速。當從集中式模式切換為分布式模式時，驅動電機轉速需要快速降低；當從分布式模式切換為集中式模式時，驅動電機轉速需要快速升高。為了提高變模過程中的平順性，根據試驗所獲的經驗，當電機轉速與將要嚙合的齒輪之間的轉速差小于50 r/min時，執行進擋控制。

變模過程中，驅動電機的調速需要在很短的時間內完成并具有足夠高的控制精度，本文選用模糊-PID（fuzzy-PID）控制理論設計相應控制器［14］，其結構見圖5。圖5中，nm為驅動電機目標轉速；n為實際轉速；ΔKP、ΔKI、ΔKD分別為模糊控制器的3個輸出量，根據輸入量e和ec分別對這3個量進行選取，從而使控制器反應更快，具有更好的靜態、動態性能。

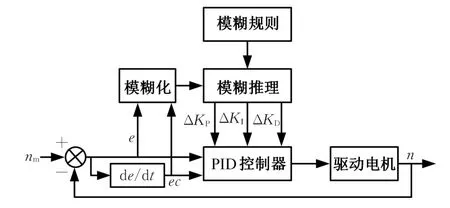
圖5 模糊PID控制器結構Fig.5 Fuzzy PID controller structure

模糊控制器輸入量e和ec分別為轉速誤差和誤差變化率，均采用三角形隸屬函數，相對于正態型隸屬函數，三角形隸屬函數的計算工作量小，可節約存儲空間且反應快，其論域范圍設置為［-6，6］。在論域上取7個模糊子集{NB，NM，NS，ZO，PS，PM，PB}，它們表示{負大，負中，負小，零，正小，正中，正大}。e和ec的隸屬度函數μ見圖6。

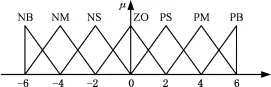
圖6 e和ec的隸屬度函數Fig.6 Membership functions of e and ec

式中，kP、kI、kD分別為模糊PID控制器解模糊之后參與計算的三個系數；T為采樣周期。

傳統PID控制器的一般表達式為

對kP、kI和kD分別進行解模糊計算

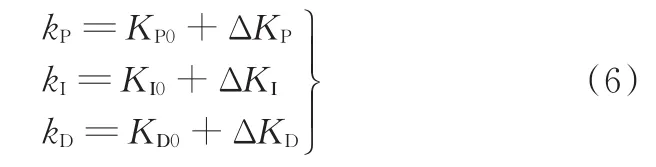
式中，KP0、KI0、KD0為PID參數的初始設計值，由傳統PID控制器的參數整定方法設計。

模糊控制規則是模糊-PID參數自整定控制器設計的重點，合適的模糊控制規則可使被控系統在最短的時間內穩定到期望的工作狀態，根據實踐經驗采用Mamdani推理法和加權平均法去模糊化，建立ΔKP、ΔKI和ΔKD的自整定規則，其模糊規則見表1～表3。

2.3 變模執行機構控制器設計

變模控制過程中，以滿足變模換擋時間要求D下的沖擊度最小為目標，選取預測函數控制（predictive function control，PFC）設計控制器進行變模執行電機的控制。PFC是預測控制范疇的一種控制方法，包含預測控制中預測模型、滾動優化和反饋校正的功能［15-16］。PFC理論中控制量由一組與過程特性和跟蹤值有關的基函數組成，使用基函數對目標控制量進行優化，通過基函數的權重系數求控制量。

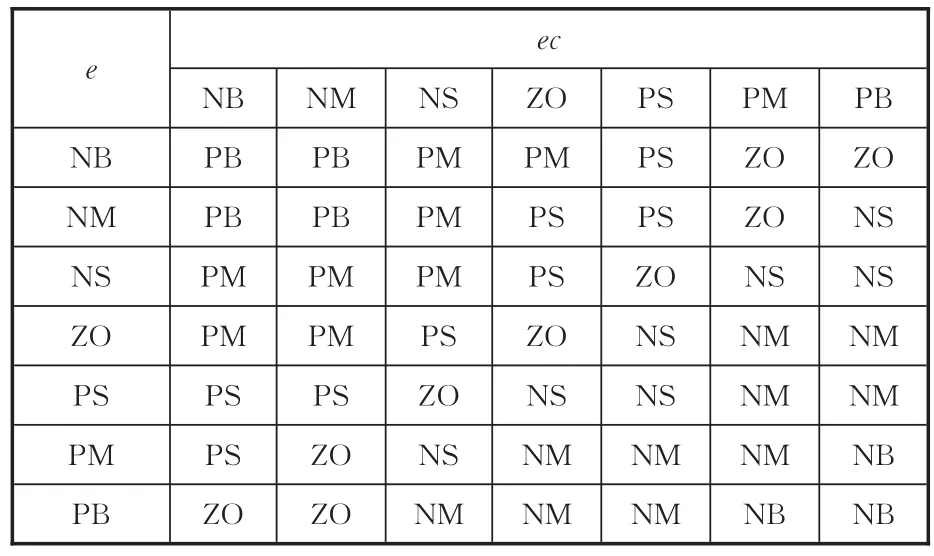
表1 ΔKP的模糊規則Tab.1 ΔKPfuzzy rules

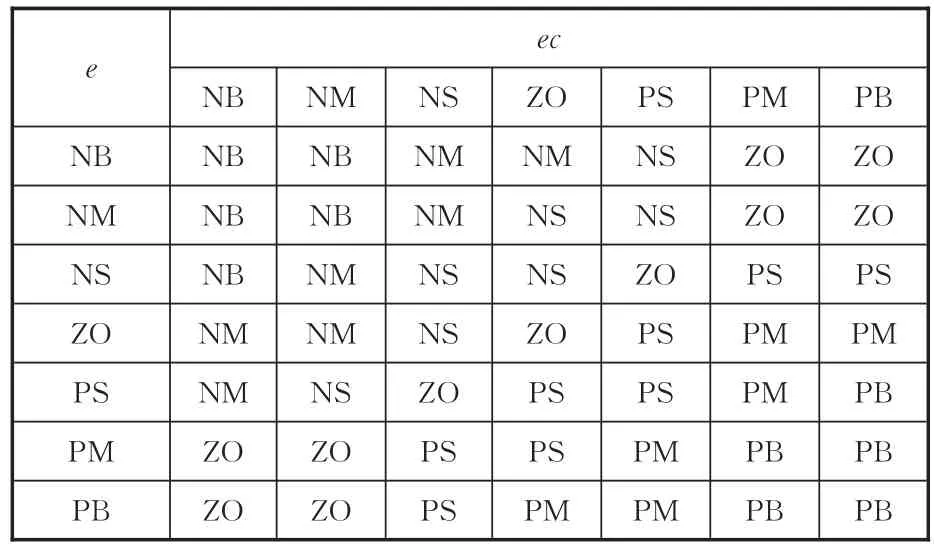
表2 ΔKI的模糊規則Tab.2 ΔKIfuzzy rules

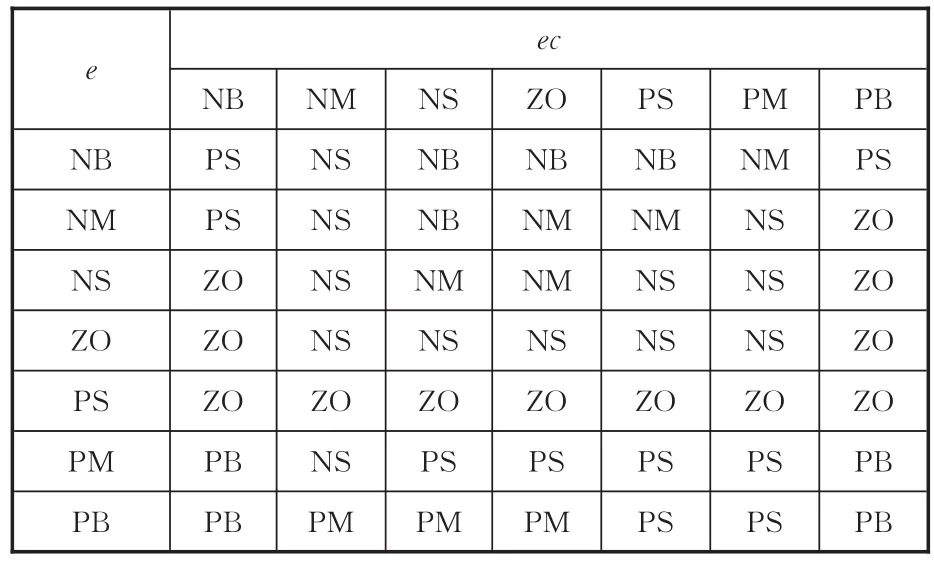
表3 ΔKD的模糊規則Tab.3 ΔKfuzzy rules

根據文獻［17］給出的詳細控制步驟進行變模電機角位移的參考軌跡跟蹤。該參考軌跡

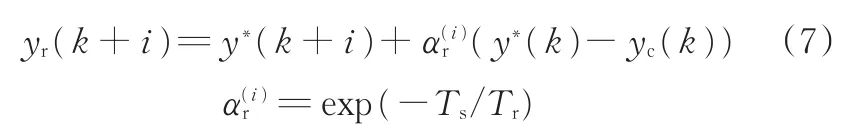
式中，y?(k+i)為控制器的期望軌跡；yc(k)為模型的實際輸出；Ts為一個數據的周期；Tr為預測步數的周期總數；i為數據的個數。

3 樣機開發與臺架試驗

3.1 樣機開發與測試臺架搭建

所開發的雙模耦合驅動系統樣機見圖7，該系統采用兩臺永磁同步電機驅動。為了實現復雜控制，系統采用dSPACE/MicroAutoBox作為控制器，其可以直接下載MATLAB/Simulink的控制程序，進行快速在線仿真研究［18-19］。驅動系統的技術參數見表4。

圖7 驅動系統樣機Fig.7 Drive system prototype

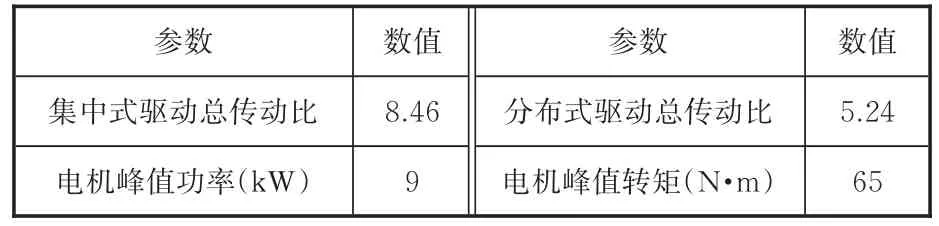
表4 驅動系統參數Tab.4 Drive system parameters

本文利用兩臺測功機分別模擬左側、右側驅動輪的不同負載和轉速情況，進行雙模耦合驅動系統的轉矩輸出特性和變模換擋控制的簡單試驗研究。所搭建的試驗臺架見圖8。

圖8 試驗臺架Fig.8 Test bench

3.2 轉矩輸出特性試驗

由于本文研究的是對開坡道雙模耦合驅動控制效果，故在進行轉矩輸出特性試驗時，假定一側測功機提供負載，另一側測功機不提供負載，有負載測功機轉速定在100 r/min，無負載測功機處于自由狀態，從而可以輕松模擬單側驅動滑轉情況。為避免無負載測功機轉速提升過快，控制加速踏板開度在5%以內。

雙模耦合驅動系統處于集中式驅動模式下測得的轉矩與轉速變化曲線見圖9，當無負載側半軸的轉速增加到416 r/min時結束此組試驗。可以看出，無負載側半軸的驅動轉矩只是隨著有負載側轉矩的增大而輕微增大，但其轉速卻快速升高，這是由集中式驅動時差速器將驅動力矩向兩側大致平均分配的轉矩輸出特性決定的，無負載側測得力矩加上慣性力矩的和基本等于有負載側力矩值去除差速器鎖止系數影響的部分。

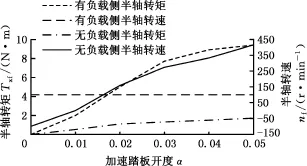
圖9 集中式驅動轉矩與轉速Fig.9 Torque and rotational speed of centralized drive

雙模耦合驅動系統處于分布式驅動模式下將采用有負載半軸一側的電機單獨驅動，測得的轉矩與轉速變化曲線見圖10。在5%以內的加速踏板開度下，有負載端轉矩達到16.2 N·m，而無負載端轉矩雖然隨著有負載端轉矩的增大而增大，但增幅非常微小，最大轉矩僅為0.2 N·m。由于轉矩大小無法克服測功機軸的摩擦力矩，整個過程中無負載側轉速基本為零。這說明差速器在分布式驅動模式下對系統轉矩傳遞的影響基本可以忽略不計，兩側半軸的轉矩完全受兩側驅動電機獨立控制。

圖10 分布式驅動轉矩與轉速Fig.10 Torque and rotational speed of distributed drive

3.3 驅動電機調速控制試驗

在臺架上對驅動電機進行基于模糊-PID控制的主動調速試驗，其中由分布式驅動模式調至集中式驅動模式時的升速調節結果見圖11。從圖11中可以看出，實際電機轉速可以在200～250 ms內調至與目標轉速偏差小于50 r/min的區域內，且超調量很小，所制定控制策略滿足變模要求。

3.4 變模電機角位移跟蹤控制試驗

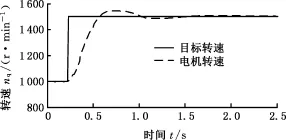
圖11 驅動電機轉速調節曲線Fig.11 Speed adjustment curveof drive motor

當兩側驅動電機調速到與目標轉速差在50 r/min以內時，變模電機在預測函數控制下對擬合的角位移曲線進行跟蹤，角位移跟蹤結果見圖12。變模過程中，結合套與同步環和結合齒圈接觸位置存在很大的隨機性，不同的結合位置會給結合套不同的阻力，同時對沖擊度也有明顯的影響，所以在角位移跟蹤過程中存在一定的誤差，但是并不影響變模控制的可靠性。所設計的預測函數控制器可以實現對擬合角位移的準確跟蹤。

圖12 角位移跟蹤曲線Fig.12 Angular displacement tracking curve

4 試驗樣車開發與對開坡道試驗

4.1 試驗樣車開發

為了驗證裝配雙模耦合驅動系統的電動汽車在對開坡道上的驅動控制效果，基于某國產微型汽車的車身和底盤結構改裝了驅動系統搭載試驗樣車，整車參數見表5。

表5 整車參數Tab.5 Vehicle parameters

4.2 驅動控制效果驗證

試驗車在坡度為6°的對開坡道上進行起步加速，右側車輪在作為高附著系數路面的干燥水泥路面上，左側車輪在涂抹洗滌液后的作為低附著系數路面的地板革上。試驗車、雙模耦合驅動系統、試驗用的轉向盤轉角和轉矩傳感器以及進行車速和車身姿態測量的差分GPS等設備的裝車情況見圖13。

圖13 試驗車及試驗設備Fig.13 Test car and test equipment

為了比較車輛在對開坡道上采用分布式驅動、集中式驅動與雙模耦合驅動的不同起步加速控制效果，利用所開發的雙模耦合驅動系統分別以上述3種驅動模式進行試驗。在雙模耦合驅動過程中，剛開始采用集中式驅動模式，當識別到出現單側驅動輪滑轉時，自動切換為分布式驅動模式，得到的車輛運行狀態曲線見圖14。試驗過程中每次發車地點相同，整個行駛過程中坡道角均保持一致。

由試驗結果可見，采用集中式驅動時，左輪很快發生滑轉，該輪地面驅動力大幅減小，此時由于差速器等轉矩傳遞特性的影響，右輪也不能夠提供足夠大的地面驅動力，導致試驗車基本無法行駛；采用分布式驅動時，雖然左輪也會發生滑轉而減小驅動力，但右輪不會受到影響，可以維持大驅動力輸出，車輛可以起步加速爬坡，約在第9 s時左輪離開地板革路面，即試驗車離開對開坡道而駛上單一坡道，此后降速停車結束試驗；采用雙模耦合驅動時，剛開始為集中式驅動模式，左輪很快發生滑轉，此時控制器控制雙模耦合驅動系統切換到分布式驅動模式，從而使車輛獲得繼續加速能力。

集中式驅動模式下，由于兩側車輪地面驅動力接近，用于維持車輛行駛轉向的轉向盤轉角和轉矩較小；分布式驅動模式下，兩側車輪地面驅動力差異較大，為維持車輛直線行駛，需要輸入較大的轉向盤修正轉角和轉矩；采用雙模耦合驅動時，轉向盤轉角和轉矩隨驅動模式變化而改變。雙模耦合驅動系統在整個變模過程中有驅動電機降扭過程、驅動模式切換過程和變模結束后的轉矩恢復過程，會存在動力中斷，但整個變模時間不超過1 s，不會發生車輛溜坡現象。

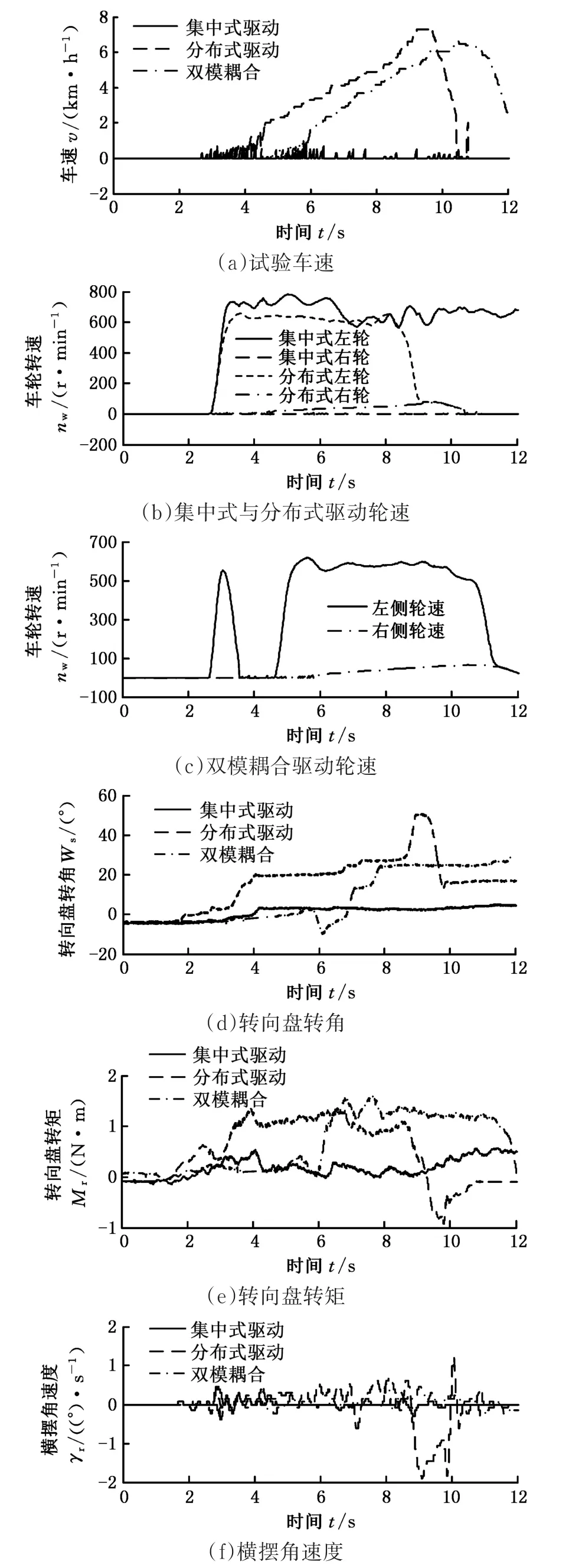
圖14 不同驅動模式車輛運行狀態Fig.14 Vehicle running status with different driving modes

由車輛橫擺角速度變化曲線可以看出，分布式驅動模式下高附著系數路面驅動輪可以獲得比低附著系數路面驅動輪更大的地面驅動力，二者之間的差異會導致車輛發生橫擺運動，特別是駛出對開路面瞬時會存在明顯的橫擺振蕩，說明分布式驅動模式在對開坡道行駛條件下會獲得比集中式驅動模式更優異的通過性能，但有必要進行橫擺運動控制。采用雙模耦合驅動可以適時選取集中式與分布式驅動模式，獲得更好的整車動力學性能。

5 結論

（1）集中式驅動作為一種常規驅動模式被電動汽車廣泛采用，但其在對開坡道上無法保證車輛的通行能力；相對而言，分布式驅動由于可以實現各輪的單獨驅動，可能充分利用地面附著條件，具有更好的通過性能。

（2）雙模耦合驅動可以充分利用集中式和分布式驅動的優勢。差速器作為關鍵力矩傳遞部件，對于分布式驅動模式下的兩側驅動力矩的分配基本不產生影響，該部件不但無負效應，反而增加了驅動系統的靈活性。

（3）基于模糊-PID控制的驅動電機主動調速與基于PFC的變模機構角位移控制相結合，可以保證變模的準確性并滿足整車的最佳驅動模式需求，變模時間在可接受范圍內。

（4）基于分布式驅動技術實現雙模耦合驅動系統對開坡道的驅動防滑控制，可以進一步提高車輛通過性能，有必要繼續研究相關的耦合控制方法；另外，如何保證雙模耦合驅動系統變模時的整車平順性、變模的可靠性，仍是需要進一步深入研究的內容。