融合車、路、人信息的電動汽車續駛里程估算

高建平 高小杰 郗建國

1.河南科技大學車輛與交通工程學院，洛陽，471003

2.河南科技大學機械裝備先進制造河南省協同創新中心，洛陽，471003

0 引言

續駛里程是人們購買電動汽車時重點考慮的問題之一。續駛里程短及目前充電樁等基礎設施的不完善，嚴重影響了人們對電動汽車的購買動力。針對這一問題，除了發展動力電池技術之外，還需要更加準確實時地預測續駛里程等參數［1-2］，以提升用戶感受，加快電動汽車的推廣應用。目前針對實際不同行駛工況下電動汽車剩余續駛里程及實時估計的研究較少，特別是關于駕駛風格的不同對續駛里程估算的影響，以及對估算結果的進一步優化的研究文獻更是鮮見。尹安東等［3］通過工況識別，實現了對當前車輛能耗的預測，完成車輛續駛里程估算，但其研究中未考慮駕駛員信息；劉光明等［4］在建立電池荷電狀態的實時估算模型及電池溫度預測模型的基礎上，進一步建立了電池剩余可用能量預測模型，實現了對車輛續駛里程的預測，但其研究也未考慮駕駛員因素；ZHANG等［5］在里程估計算法中直接應用剩余能量預測值，其方法基于Telematics System提供道路信息和汽車狀態信息，但未包含駕駛員信息；OLIVA［6］等應用粒子濾波方法對SOC和續駛里程值進行估計，未專門考慮行駛工況及駕駛員因素對續駛里程估算的影響；SIY等［7］和PANDIT等［8］通過計算當前時間段的能耗來預測下一時間段能耗，再根據電池剩余能量來預測剩余續駛里程，此方法估算結果比較保守，未在能耗預測過程中考慮駕駛員因素，并且在工況急劇變化情況下存在估算不穩定的問題。

筆者通過采集大量的鄭州市純電動公交車實際行駛工況數據，選出典型鄭州市行駛工況運動學片段作為學習矢量量化（learning vector quantization，LVQ）神經網絡學習的典型樣本，在此基礎上建立主成分分析（principal component analysis，PCA）與LVQ神經網絡相結合的行駛工況識別模型，并在工況識別基礎上建立駕駛風格識別模型，實現對車輛能耗的準確預測，進而實現對車輛剩余續駛里程的估算。針對由于工況及電池可用能量變化時估算結果頻繁波動變化的情況，通過卡爾曼濾波（Kalman filter，KF）對輸出剩余續駛里程進行了優化，并通過實際工況進行續駛里程仿真分析及半實物測試驗證。

1 典型工況訓練片段選取

1.1 汽車行駛工況數據采集

將車載終端設備（圖1）安裝于試驗公交車輛，行駛數據由車載終端設備實時采集，采樣頻率為1 Hz［9］。通過通用分組無線服務技術網絡，將采集到的車輛運行過程中的相關信息傳送到車輛遠程管理服務平臺，從中國汽車工況信息化系統查詢并下載數據。

圖1 車載終端設備Fig.1 Vehicle terminal equipment

1.2 運動學片段特征參數提取

行駛工況可以看作是眾多運動學片段［6］的組成。參考文獻［10-13］，選取可以全面表征運動學片段的速度、加速度、時間、距離以及加減速等特征的12個特征參數對其進行描述，12個特征參數分別為：平均運行距離s，m；平均速度vavg，m/s；最大速度vmax，m/s；運行時長tall，s；怠速時間till，s；加速時間tacc，s；減速時間tdec，s；勻速時間tcon，s；最大加速度 amax，m/s2；最小加速度 amin，m/s2；減速段平均加速度aavg-，m/s2；加速段平均加速度aavg+，m/s2。

將實際采集的300多萬組行駛工況數據通過MATLAB軟件編程進行處理，得到20 182個有效運動學片段，進而編程處理得到一個樣本數量（行）×特征值（列）矩陣，如表1所示。

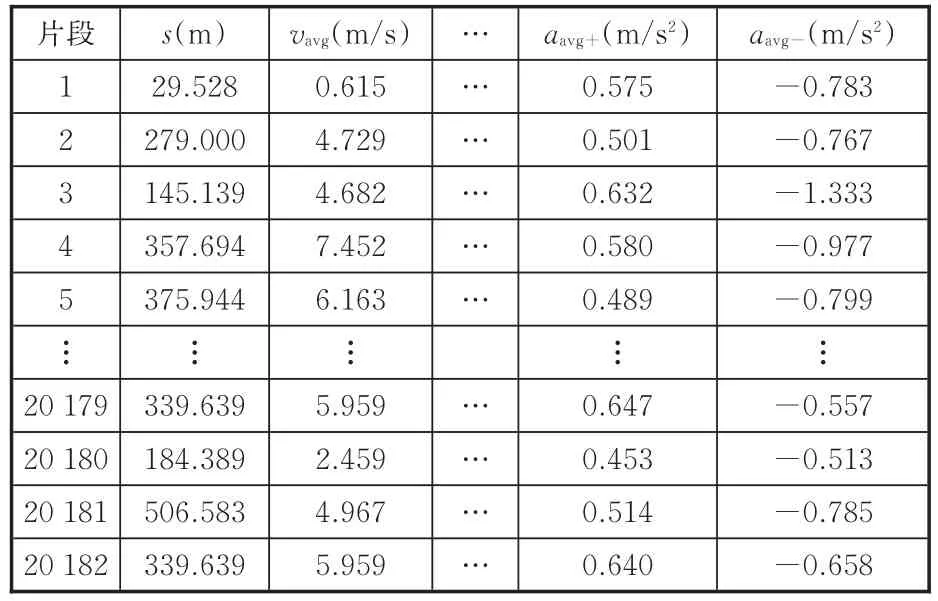
表1 運動學片段特征參數Tab.1 Characteristic parameters of kinematic segments

1.3 主成分分析

主成分分析［10］可以通過消除變量之間的相關性，最終得到幾個綜合變量來反映所研究問題的大部分信息，該分析方法不僅可以反映事物的本質，而且可以簡化后續的計算。

針對上述矩陣進行主成分分析。得到的12個主成分的特征值、貢獻率和累積貢獻率見表2，各成分使用Mi（i=1，2，…，12）表示，前4個主成分的累計貢獻率已經達到83.767%，所包含的特征參數信息能夠用于表征整個運動學片段，故前4個主成分用于聚類分析。

1.4 模糊C均值聚類

1.4.1 最佳聚類數的選取

利用模糊C均值聚類分析對20 182個運動學片段分別進行2～20類聚類。通過描述類間離差矩陣分離度、類內離差矩陣緊密度的CH（Calinski-Harabasz）指標（CH值）對劃分為2～20類工況進行評價，從而確定最佳聚類。CH值表達式如下：

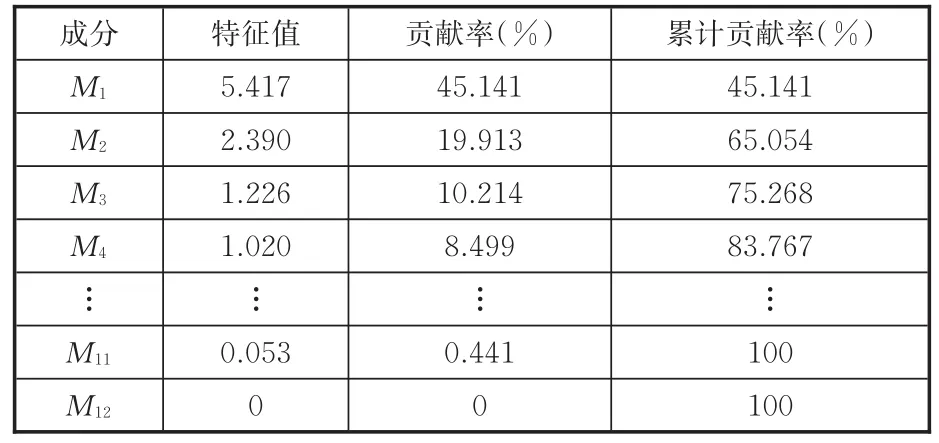
表2 各個成分特征值、貢獻率、累積貢獻率Tab.2 Eigen values，contribution rates and cumulativecontribution rates of each component

式中，n為行駛工況聚類數目；k為當前所處工況類型；trW（k）為相同類工況所有片段離差矩陣W（k）的跡；trB（k）為不同類行駛工況之間離差矩陣B（k）的跡。

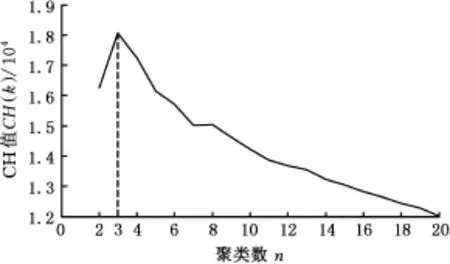
圖2 不同聚類數CH指標Fig.2 CH index of different cluster number

CH值越大表示聚類所得的相同類的行駛工況之間的距離和越小，不同類行駛工況之間的距離和越大，聚類數選取越佳，由圖2可知，將鄭州市行駛工況分成3類為最佳分類數。

1.4.2 模糊C均值聚類分析

表3所示為通過模糊C均值聚類（3類）后各類工況綜合特征值及全部數據綜合工況特征值，其中，Pi為怠速比例，Pa為加速比例，Pd為減速比例，Pc為勻速比例。第1類怠速比例高達53.201%，平均每個片段運行時間26.450 s，平均速度僅為6.386 km/h，說明車輛在此工況行駛時，車流量被嚴重限制，代表車輛處于城市鬧市區工況；第2類怠速比例30.400%，平均每個片段運行時間42.673 s，平均速度15.941 km/h，代表車輛處于城市生活區工況；第3類怠速比例僅13.110%，平均每個片段運行時間98.777 s，且平均速度20.542 km/h，說明在該道路行駛時，車流量較小、較暢通，代表車輛在城市郊區工況。

1.5 典型工況片段選取

計算各類樣本中的各個片段與該類總樣本數據的相關系數ρXY，并從3類行駛工況中分別選取與該類所有數據相關系數大的片段，用于LVQ神經網絡訓練。ρXY的表達式為

表3 各類數據綜合特征值Tab.3 Overall characteristic parameters of each category

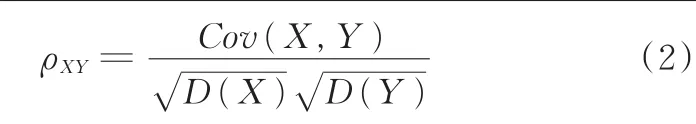
式中，X為各個工況片段特征參數數據；Y為總體樣本工況特征參數數據；Cov（X，Y）為X、Y的協方差；D（X）、D（Y）分別為X、Y的方差。

2 基于PCA-LVQ神經網絡的汽車行駛工況識別

車輛在實際使用過程中，由于行駛工況經常發生變化，而不同工況對應的能耗有一定的差別，因此能夠實時準確地識別工況類別，對剩余續駛里程的更準確估計起著重要作用。

為了更加準確地識別汽車行駛過程中的工況類別，應采用較多的行駛工況特征參數，但是由于工況特征參數之間有一定的相關性，且特征參數的量綱不盡相同，因此直接利用工況特征參數對車輛行駛工況進行識別，會在很大程度上影響識別準確性。通過對全面、系統反映運動學片段的眾多特征變量作主成分分析，并將其作為LVQ神經網絡識別模型輸入，不僅能大大縮短網絡訓練時間，簡化計算，而且可消除通過特定特征參數進行工況識別時量綱的影響，提高了LVQ網絡模型識別的準確率。

基于主成分分析（PCA）和LVQ神經網絡的行駛工況識別流程圖見圖3，主要包括兩部分：①離線LVQ樣本訓練部分。利用選取的代表性運動學片段對其主成分進行提取，并進行LVQ神經網絡訓練。②在線LVQ工況識別部分。對采集的汽車行駛過程中的工況數據進行特征參數提取及主成分提取，將其作為LVQ神經網絡識別模型的輸入層，進而輸出該片段所屬的行駛工況類型，并進行實時識別及更新。考慮到識別周期對識別效果的影響，結合實時處理能力及所采集實際行駛工況數據的片段長度，選取120 s為識別周期［14］。

圖3 工況識別流程圖Fig.3 Flow chart of working condition identification

2.1 LVQ神經網絡

LVQ神經網絡［15］結構如圖4所示，由輸入、競爭和線性輸出3層神經元組成。圖中，P為R維的輸入模式；S（1）為競爭層神經元個數；W(1.1)I為輸入層與競爭層之間的連接權系數矩陣；n（1）為競爭層神經元的輸入；a（1）為競爭層神經元的輸出；W(2.1)L為競爭層與線性輸出層之間的連接權系數矩陣；n（2）為線性輸出層神經元的輸入；a（2）為線性輸出層神經元的輸出；ndist為計算輸入層向量與競爭層向量之間的歐氏距離；compet（·）為競爭層傳遞函數；purelin（·）為線性函數。

圖4 LVQ神經網絡結構Fig.4 Architecture of LVQ neural network

2.2 工況識別樣本訓練

對選取的各類典型工況訓練片段進行特征參數提取，進而提取主成分，作為LVQ神經網絡訓練樣本數據，用于LVQ神經網絡的行駛工況識別模型訓練，訓練過程如圖5所示。根據訓練樣本的主成分及所屬類別不斷調整競爭層權值，訓練結束之后，將最終競爭層權值應用于行駛工況識別。

2.3 工況識別模型驗證

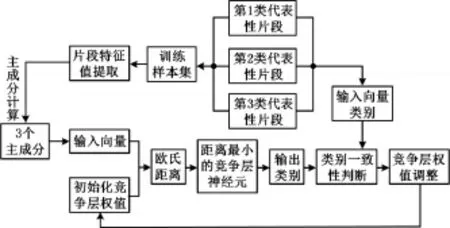
圖5 樣本訓練過程Fig.5 Sample training process

對采集的行駛工況數據的20 182個有效片段（包括6 294個第1類工況片段、8 325個第2類工況片段、5 563個第3類工況片段）進行各個片段特征參數提取，進而提取主成分并作為測試集，結果如表4所示。由表4知，第1類和第3類識別正確率較高，均超過90%；第2類相對較低，由于第2類工況處于第1、3類之間，有一部分工況片段與第1、3類相似度高，故綜合正確率為90.17%。由此可知，基于PCA-LVQ的行駛工況識別法可以更加準確地實時識別出當前所處行駛工況。

表4 不同工況類型識別結果Tab.4 Recognition accuracy of different driving cycle

3 駕駛員駕駛風格識別

通常將駕駛員的駕駛風格劃分為3類：經濟型、一般型、動力型，不同駕駛風格的駕駛員踩加速踏板、制動踏板的幅度及速度不同。但由于駕駛員對加速踏板、制動踏板的使用會受到車輛實際行駛工況的影響，因此駕駛風格的識別需要在工況識別的基礎上進行才更加合理。

駕駛員是“車-路-人”系統中的重要環節，駕駛風格又是駕駛員在道路上的動態行為，相同的公交線路，相似的行駛工況下，同型號電動汽車不同駕駛風格的能耗差異往往較大［16］。因此通過識別當前行駛工況，并在此基礎上對駕駛風格進行識別，才能更加準確地得到純電動汽車行駛過程中的能量消耗。

平均加速度和加速度標準差大小可以反映駕駛員在駕駛車輛過程中對動力性的要求及加速度的分散程度，本研究聯合采用平均加速度和加速度標準差參數對駕駛風格進行模糊識別。

加速度平均值

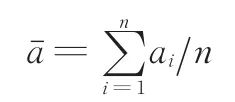
式中，n為采樣次數；ai為加速度第i次采樣值，m/s2。標準差

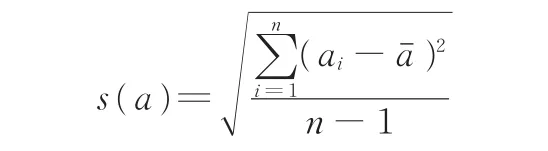
采用K均值聚類的方法，聯合采用平均加速度與加速度標準差參數對20 182個運動學片段進行3類聚類分析。聚類得到3類聚類中心以（aˉ，s（a））表示為（0.240，1.742）、（0.310，2.546）、（0.430，3.579），分別作為經濟型、一般型、動力型駕駛風格工況片段的聚類中心。通過式（2）相關系數計算公式選取各類典型駕駛風格片段用于模糊控制器參數的確定。

模糊控制主要借鑒專家的經驗來選擇控制器的結構和參數，但僅僅靠專家的經驗很難得到滿意的效果。本文模糊控制器的模糊規則比較簡單，因此需要對隸屬度函數進行優化。采用典型駕駛風格片段利用遺傳算法優化模糊控制器隸屬度函數，得到平均加速度、加速度標準差隸屬度函數（圖6）。駕駛風格推理規則表見表5。

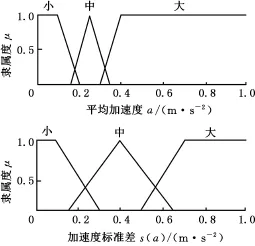
圖6 平均加速度及加速度標準差隸屬度函數Fig.6 Membership function of average acceleration and standard deviation of acceleration

表5 駕駛風格推理規則表Tab.5 Inference rule table of driving style

4 動力電池剩余可用能量估計

電池作為復雜的電化學系統，在不同狀態、不同工況下的可用能量均不相同［17］。本文選取的某公司8 m純電動客車采用標稱電壓為518.4 V的磷酸鐵鋰LiFePO4動力電池組，其額定容量為172 A·h。根據鋰電池基本特性，在綜合考慮三種簡化電化學模型基礎上，建立了鋰電池電化學復合模型［18］。該模型不僅考慮了溫度的影響，而且將充放電倍率及充放電方向考慮在內，能準確反映鋰電池的動態特性。其數學表達式如下：

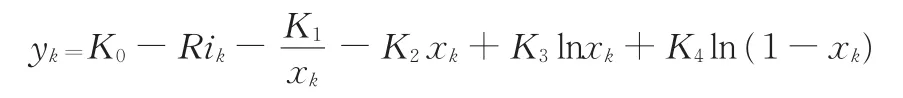
式中，yk為電池工作電壓；ik為k時刻電流值；R為電池內阻，充電時R=RC（ik為負），放電時R=Rd（ik為正）；xk為k時刻的瞬時荷電狀態；K0、R、K1、K2、K3、K4為復合電化學模型匹配系數。

對電池荷電狀態（SOC）值作如下定義：

對式（3）進行離散化處理得

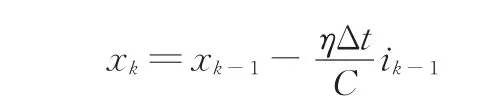
式中，xk為k時刻SOC值；ik-1為k-1時刻電流值；Δt為時間間隔。

由此，得到鋰電池的狀態空間模型。狀態方程為

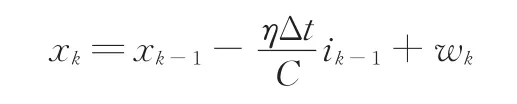
觀測方程為

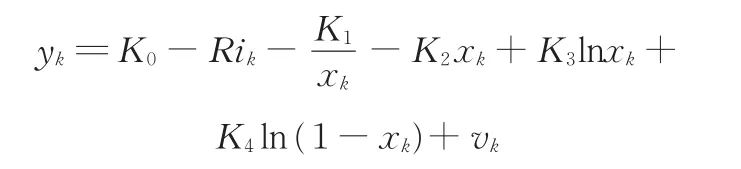
式中，wk、vk分別為均值為0的高斯白噪聲。

利用磷酸鐵鋰離子動力電池組試驗獲得電流、電壓和真實SOC值，采用自適應模擬退火（ASA）算法對電化學復合模型參數進行辨識，得到最優充放電內阻及模型匹配參數。參數辨識結果如表6所示。

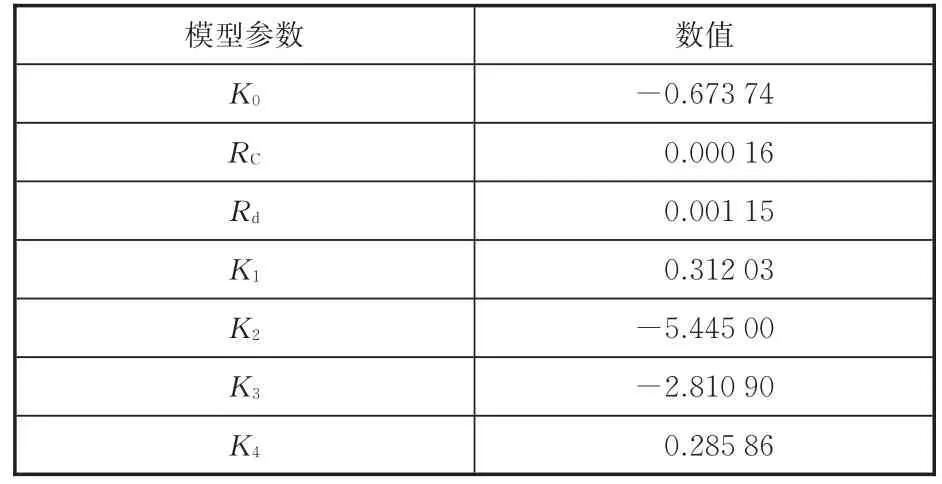
表6 參數辨識表Tab.6 Parameter identification table

對電動汽車行駛過程來說，電池的剩余放電能量ERDE是指以某一工況行駛時，從當前時刻直至電池放電截止這一過程中，電池累計能提供的能量。電池剩余能量值

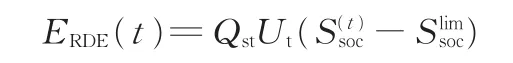
式中，ERDE（t）為當前時刻電池剩余能量值；為允許的放電截止SOC值（本文取0）；Qst為電池標準容量；Ut為放電平均電壓。

5 融合車、路、人信息電動汽車續駛里程估算

5.1 估算方法

本文在確定的汽車本身狀態下，通過實時識別純電動汽車行駛過程中不同行駛工況、駕駛員駕駛風格，從而更加準確地得到行駛過程中的能耗，并結合磷酸鐵鋰LiFePO4電池剩余可用能量，進而實現剩余續駛里程的實時預測。

為了更好地反映車輛行駛能耗的最新變化，采用調整當前行駛工況的單位里程能耗與歷史單位里程能耗的權值的方法，即當前時刻路段工況類型平均能耗采用較大的權重，而歷史單位里程能耗采用較小的權重，計算公式如下：

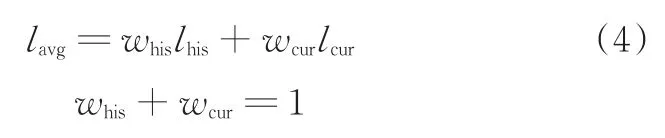
式中，lavg為平均單位里程能耗；whis為歷史單位里程能耗的權重；lhis為歷史單位里程能耗；wcur為當前單位里程能耗的權重；lcur為當前單位里程能耗。

融合車、路、人信息的電動汽車剩余續駛里程估算方法如圖7所示。

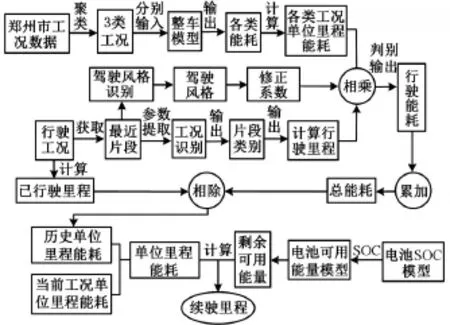
圖7 融合車、路、人信息的電動汽車續駛里程估算Fig.7 Driving range estimation for electric vehicles through vehicles，roads，and human information fusion

首先將采集的鄭州市工況數據聚類成3類工況，分別輸入整車模型，計算得到各類工況的單位里程能耗。通過獲取行駛過程中最近120 s的一個片段，并對該片段進行工況識別、駕駛風格識別，計算行駛過程所消耗的能耗，累加得出總能耗。通過速度積分得到車輛行駛里程數，進而計算歷史單位里程能耗，并結合當前工況單位里程能耗，計算能動態反映車輛工況最新變化的單位里程能耗，并結合動力電池剩余可用能量實時計算得到剩余續駛里程的實時預測。

5.2 估算實例

5.2.1 各類工況單位里程平均能耗

選取某公司8 m純電動客車為研究對象，圖8為該電動客車整車動力系統結構簡圖。表7為所示主要技術參數，整車模型在前向仿真軟件AVLCRUISE中搭建，并通過AVL-CRUISE里的外部電池接口將在MATLAB/Simulink里建立的動力電池電化學復合模型鏈接到AVL-CRUISE中。通過將采集到的3類行駛工況分別輸入到整車模型，仿真計算出各類行駛工況的單位里程平均能耗。

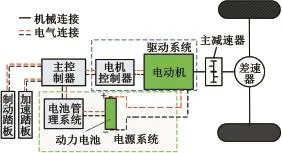
圖8 系統結構簡圖Fig.8 Schematic diagram of system

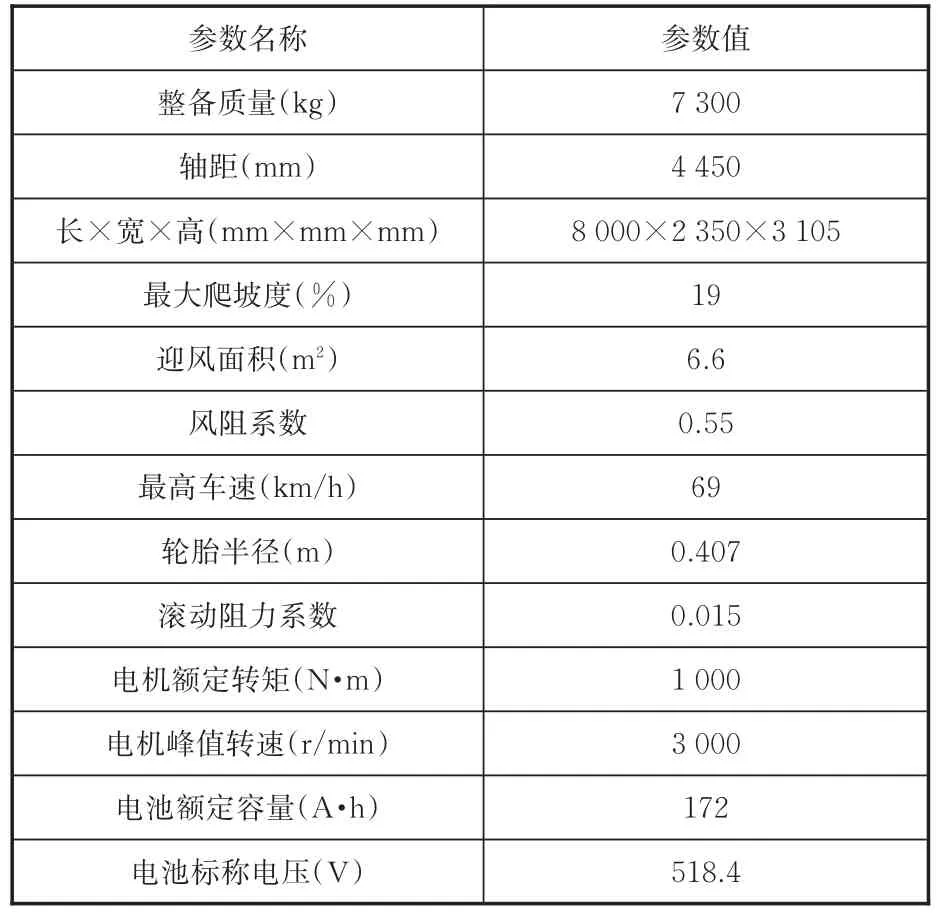
表7 整車技術參數Tab.7 Vehicle technical parameters

數據采集過程中，會由于設備傳輸問題及駕駛員操作失誤，導致所采集的實驗車工況數據有噪點，從而影響到電機的工作狀態，導致仿真的電耗結果與實際值偏差較大，因此在仿真之前需對鄭州工況進行平滑處理，所采用平滑曲線濾波器定義為［7］

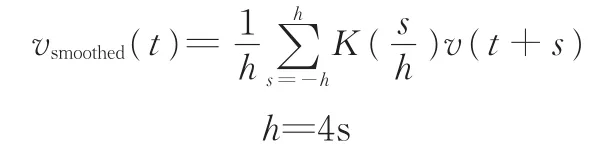
式中，K（x）為t時刻前后速度的權值。

K（x）函數如下：

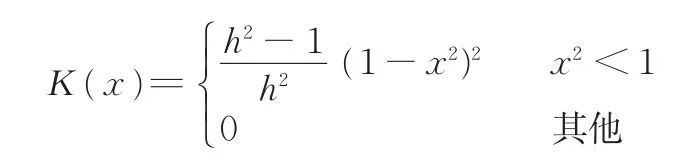
圖9為隨機選取的一段工況數據濾波前后的時間（t）-速度（v）曲線對比圖。

圖9 工況數據濾波前后對比圖Fig.9 Comparison chart of condition data before and after filtering

通過MATLAB/Simulink與AVL-CRUISE聯合仿真得出8 m純電動客車在第1、2、3類車輛行駛工況單位里程平均能耗分別為5 076 W·h/km、6 025 W·h/km、4 620 W·h/km。

5.2.2 續駛里程估算

由式（4）可得動態反映車輛工況最新變化的單位里程能耗lavg。

已消耗總能量

歷史單位里程能耗

lhis=Ecost/S

剩余續駛里程

Sres=ERDElavg

式中，Ecost為純電動客車歷史工況總消耗；Et為當前汽車單位里程能耗；ttotal為行駛總時間；S為純電動客車已行駛里程；ERDE（t）為當前時刻電池剩余能量值。

6 仿真分析及半實物測試驗證

6.1 仿真分析

隨機選取一部分車載終端設備采集的實車行駛工況數據作為測試數據，利用MATLAB/Simulink與AVL-CRUISE聯合仿真，從而驗證所采用的融合車、路、人信息的電動汽車續駛里程估算方法的準確性和可行性。

分別采用工況識別法和工況識別與駕駛風格識別相結合的方法得到估算值，估算值與實際值的比較結果如圖10所示。由圖10可知兩種估算方法在估算初始階段波動較大，由于歷史工況數據較少，且隨著工況的變化，單位里程能耗變化較大，導致估算結果隨之變化較大。但隨著歷史數據的逐漸積累，單位里程能耗逐漸收斂于一個值（圖11），從而使得兩種方法估計的剩余續駛里程波動也隨之變小。兩種估算方法所得的剩余里程估算與實際值之間的誤差對比如表8所示。由表8比較可知，采用融合車、路、人信息的估算方法是可行的，且相比工況識別法精度更高。

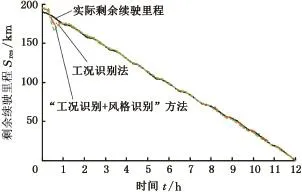
圖10 兩種估算方法對比Fig.10 Comparison of two estimation methods

圖11 單位行駛里程能耗Fig.11 Energy consumption per unit mileage

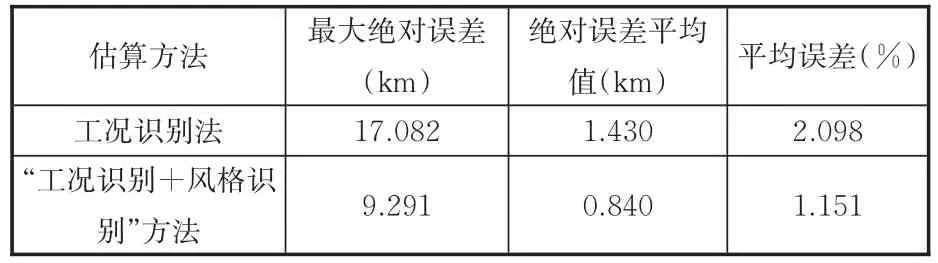
表8 兩種估算方法誤差對比Tab.8 Error comparison of two estimation methods

均方根誤差（REMD）被廣泛應用于不同數據之間偏差的對比，尤其是基于模型估計的預測值與真實值之間的對比。為了進一步驗證采用融合車、路、人信息的純電動客車續駛里程估算方法的有效性，本文以均方根誤差作為評價指標，其計算式如下：

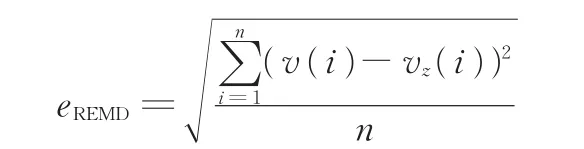
式中，v（i）為第i個剩余續駛里程預測值；vz（i）為對應時刻剩余里程真實值；n為總預測次數。

工況識別法和“工況識別+風格識別”方法對剩余里程估算結果的均方根誤差分別為2.609 km和1.536 km。可以看出，采用的融合車、路、人信息的“工況識別+駕駛風格識別”方法與工況識別法相比，均方根誤差降低了41.13%。

為避免由于工況及駕駛風格改變時，儀表上實時顯示的剩余續駛里程頻繁跳變，對采用融合車、路、人信息的估算結果采用卡爾曼濾波（KF）方法再次優化處理，優化后剩余里程顯示過渡更加平滑，從而避免駕駛員產生焦慮情緒。圖12為KF優化前后剩余續駛里程曲線對比及局部放大圖。經過KF優化后絕對誤差平均值為0.801 km，平均誤差為1.120%，均方根誤差為1.308 km，可知經過KF優化后各種誤差進一步減小，估算精度得到提高。

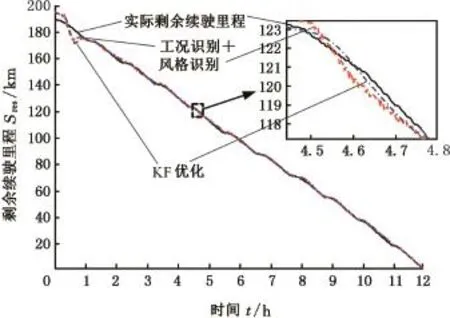
圖12 KF優化前后剩余續駛里程曲線對比Fig.12 Contrast before and after Kalman optimization

6.2 半實物測試驗證

引入半實物仿真平臺進行進一步驗證。平臺硬件系統主要由dSPACE、CANoe及駕駛員模擬器組成，軟件系統主要包括AVL-CRUISE、MATLAB及dSPACE自帶的數據監控軟件ControlDesk。控制對象采用dSPACE的I/O接口連接，試驗采用兩路ADC模數轉換通道分別采集真實駕駛員的油門踏板和制動踏板信號，一路局域網通道實現數據的接收與發送。CANoe作為CAN通信控制器，可真實模擬實車數據間的信號傳輸，并且由真實駕駛員跟隨目標車速踩下油門和制動踏板，使該仿真試驗更接近于真實實車試驗，測試方案如圖13所示。

半實物測試表明：采用融合車、路、人信息的純電動客車續駛里程的估算方法，平均誤差2.457%，絕對誤差平均值1.392 km，均方根誤差2.180 km，各類誤差較小，進一步驗證了融合車、路、人信息的電動汽車剩余續駛里程方法的準確性及可行性。

7 結論

圖13 半實物仿真試驗方案Fig.13 Hardware in the loop simulation test scheme

（1）通過主成分分析和聚類分析法，并利用CH指標，確定汽車行駛工況的最佳聚類數，并選出基于大數據的、符合鄭州市交通特點的公交車各類實際代表性行駛工況片段，用于工況識別模型的訓練。

（2）建立基于主成分分析和LVQ神經網絡的行駛工況識別模型，綜合識別正確率達90.17%，并在工況識別的基礎上，通過模糊控制的方法對駕駛風格進行識別，增加駕駛員信息，進而進行融合車、路、人信息的電動汽車剩余續駛里程仿真估算，并利用卡爾曼濾波對續駛里程估算結果作進一步優化，提高了剩余里程估算精度。

（3）采用實車采集的工況數據對純電動客車估算方法仿真分析對比驗證，結果表明融合車、路、人信息的電動汽車剩余續駛里程估算方法誤差較小，可有效提高估算精度；半實物測試結果表明，所采用的估算方法是可行的。