基于粒子群優化支持向量機算法的行駛工況識別及應用

石 琴 仇多洋 吳 冰 李一鳴 劉炳姣

合肥工業大學汽車與交通工程學院，合肥，230009

0 引言

在新能源汽車的研發過程中，行駛工況識別得到越來越廣泛的應用。對于混合動力汽車，在制定的能量管理策略中，如果能夠識別當前行駛工況的特點，實時調整能量控制參數值，實現不同動力源之間功率分配最優，則可進一步提高整車燃油經濟性［1-7］。而對于純電動汽車，準確識別出實時行駛工況類型，獲得相應類型工況下電耗水平，有助于提高純電動汽車剩余續駛里程估算的準確性［8-9］。

當前行駛工況識別方法大致可分為三類：①采用神經網絡算法進行識別。WANG等［10］利用數理統計方法篩選出識別參數，并用學習向量量化（learning vector quantization，LVQ）神經網絡算法進行行駛工況識別；JEON等［11］定義一系列特征參數來描述行駛工況，采用Hamming網絡進行行駛工況識別；周楠等［12］應用競爭型神經網絡算法確定實時行駛工況隸屬的標準工況類型。②采用模糊控制器進行識別。田毅等［13］采用遺傳算法優化的模糊控制器對廣州和上海主干道行駛工況進行識別。③利用聚類理論進行識別。RAVEY等［14］將平均車速、停車次數、停車時間、加速度和減速度5個參數及其權重的乘積作為聚類參數，利用動態聚類理論判斷實際行駛工況所屬的標準工況類別；秦大同等［7］通過計算待識別工況與標準工況特征參數的歐幾里得距離確認行駛工況所屬類型；詹森等［3］利用遺傳算法優化的K均值聚類算法進行行駛工況識別。

上述研究中，采用神經網絡算法識別行駛工況時，訓練過程中隱含層神經元個數存在不確定性，導致識別結果存在較大差異，很難得到最優識別模型；采用模糊控制器進行行駛工況識別時，隸屬度函數大多根據經驗選擇，只有反復調試才可以提高識別精度；采用聚類理論進行行駛工況識別時，聚類中心初始值對識別結果影響較大，容易陷入局部最優解的情況，同時對輸入參數的個數比較敏感。

支持向量機（support vector machine，SVM）是根據統計學習理論的VC理論和結構風險最小化原則提出的一種針對有限樣本情況的機器學習方法［15］，大大簡化了通常的分類和回歸問題，且具有較好的魯棒性。SVM作為有監督的學習理論，沒有聚類理論中初始聚類中心的設置問題，同時避免了人工神經網絡等理論的網絡結構選擇、過學習和欠學習等問題，可廣泛用于模式識別。

為了提高SVM算法識別精度，本文將粒子群優化（particle swarm optimization，PSO）算法和SVM算法相結合，建立最優的行駛工況識別模型，分析了識別周期和更新周期對實時在線識別精度的影響；將行駛工況識別技術應用在插電式混合動力汽車的能量管理策略中，驗證了行駛工況識別有助于整車實時最優控制，并提高了混合動力的汽車燃油經濟性。

1 理論基礎

1.1 支持向量機識別算法

SVM算法基本思想是：通過非線性映射將低維空間的輸入數據映射到高維的特征空間，使其成為線性可分，在高維空間求解最優判別函數，確定分類邊界。

已知線性可分情況下訓練樣本集：{（xi，yi）}其中，xi∈Rn，yi∈{-1，+1}（i=1，2，…，l）。利用最優分類超平面ωxi+b=0對樣本進行分類，離最優分類超平面最近的兩類樣本稱之為支持向量。支持向量與最優超平面之間的距離之和為根據結構風險最小化原則，應使該距離之和最大，因此求解最優超平面的問題轉化為下述優化問題：

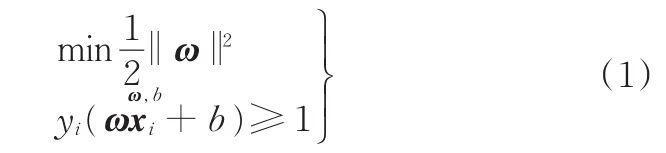
式中，ω為最優分類超平面的法向量；b為閾值，b∈R。

針對訓練樣本集大多數情況是線性不可分的，SVM引入非負松弛因子ξi，同時加入懲罰系數C。通過核函數進行非線性映射后，將上述目標函數變化為

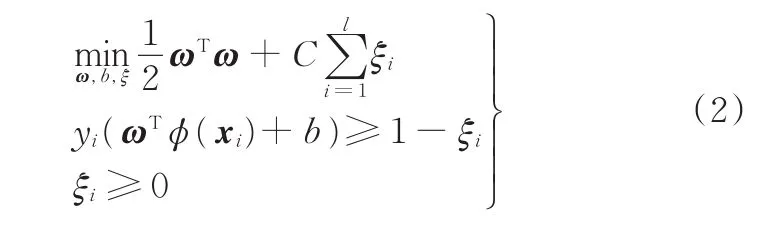
使用Lagrange乘子法求解上述最小值問題。建立Lagrange函數如下：

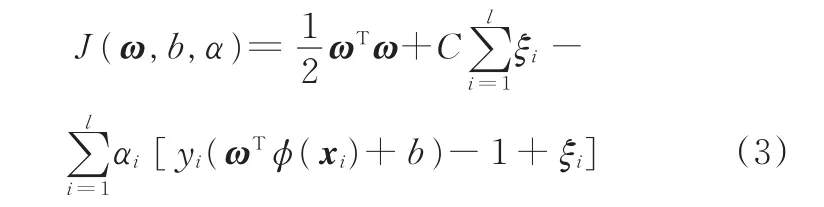
式中，αi為Lagrange乘子，是輔助非負變量。

分別對式（3）中的ω和b求偏導并置零，將結果代入式（3）可得到原問題的對偶問題：

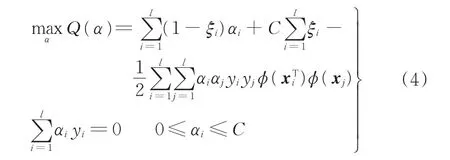
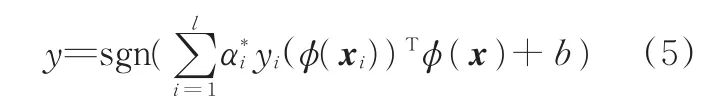
式中，x為測試樣本。

定義K（xi，x）=(φ(xi))Tφ(x)為核函數，應用最廣泛的核函數即高斯徑向基函數：

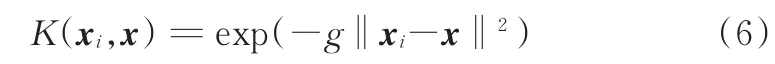
式中，g為核函數寬度。

上述推導過程可以看出，懲罰系數C與核函數寬度g的取值是影響SVM識別性能的主要因素，因此，若要提高識別精度，需確定最優懲罰系數C與核函數寬度g的取值，通常是利用k-cv交叉驗證法選擇最優的C與g。本文將C與g作為優化對象，以識別精度為適應度函數，利用粒子群優化算法尋找最優的C與g，建立最優的行駛工況識別模型。

1.2 基于粒子群優化的SVM識別算法

粒子群優化（PSO）算法具有搜索機制簡單，收斂速度快，運算量小等優點，且能夠減少和避免陷入局部最優解的情況。利用基于PSO優化的SVM算法（簡稱PSO-SVM算法）尋找最優的C和g，可避免k-cv交叉驗證法計算量大、精度不高等問題，PSO-SVM算法流程見圖1。

圖1PSO-SVM算法流程Fig.1 PSO-SVM algorithm flow

PSO-SVM算法的基本步驟如下。

（1）設置種群粒子個數為m。

（2）初始化種群中各粒子的速度和位置，得到第1代種群u（1）=［u(1)1，u(1)2，…，u(1)j，…，u(1)m］。本文的搜索空間為2維，則每個粒子包含2個變量。并將各粒子的歷史最優位置pbest設為初始位置，取粒子群全局最優位置gbest中的最優值。

（3）根據得到的種群，更新SVM算法中的懲罰系數C和核函數寬度g。

（4）利用訓練樣本訓練SVM算法模型。

（5）利用測試樣本測試SVM算法精度，即適應度函數值。適應度函數值計算表示式如下：

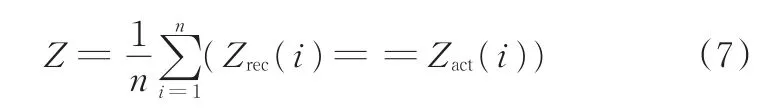
式中，Zrec為識別的工況類型；Zact為實際的工況類型；n為測試樣本數量。

（6）更新粒子速度和位置，表達式分別如下：

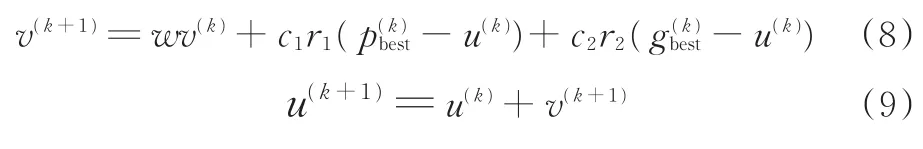
式中，w為慣性權重；r1和r2為分布于區間［0，1］內的隨機數；k為當前迭代次數，初始值為1；p(k)best為第k代個體最優粒子位置；g(k)best為第k代全局最優粒子位置；c1、c2為常數；v為粒子速度；u為粒子位置。

進而得到k+1代種群的位置：

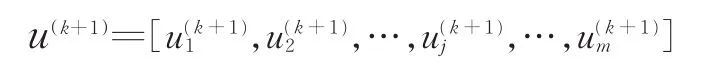
（7）計算更新后的每個粒子的適應度，并與之前經歷過的最優位置pbest所對應的適應度比較，若當前位置更好，則將其當前位置作為該粒子的pbest。

（8）將每一個粒子的適應度與全體粒子所經歷過的最優位置gbest比較，若當前位置更好，則更新gbest的值。

（9）檢查終值條件，若精度滿足預設條件，則停止迭代；若精度未滿足預設條件，則返回步驟（3）；若超出最大迭代次數，同樣停止迭代。

（10）輸出最優解。

2 算法實例分析

2.1 數據采集

在行駛工況識別的研究中，諸多文獻都定義了3類典型行駛工況［4，14，16］，即市區工況、郊區工況和高速公路工況。但隨著城市立體交通網絡逐漸形成，高架橋數量逐漸增多。而高架橋道路的行駛工況特點又有別于以上3類行駛工況，因此本文定義4類典型行駛工況，每種工況特點如下：

（1）市區工況。主要集中在城市中心地帶，十字路口多，紅綠燈多，車輛數目多，交通流量大，道路經常擁堵，車輛頻繁啟動，車速較低且停車間隙長，工況類型編號為1。

（2）郊區工況。車輛常以中速行駛，停車次數較少且停車時間較短，由于限速，車速不會超過60 km/h，工況類型編號為2。

（3）高架橋工況。車輛常以較高速行駛，雙向分割行駛，在無行人或非機動車輛的工況下行駛，無交通信號燈，限速80 km/h，工況類型編號為3。

（4）高速公路工況。與高架橋工況類似，區別在于出入口完全被控制，限制時速比高架橋工況的限速高，通常為120 km/h，工況類型編號為4。

為建立工況數據庫，需大量采集符合以上4種工況特征的行駛工況數據。本文以典型中等城市合肥市為例，進行實車道路實驗，采集4類典型行駛工況數據。通過整車CAN信號采集設備讀取CAN信號中的車輛速度、運行時間、行駛里程等信號，利用車輛綜合性能記錄儀將信號實時保存在車載電腦中，形成行駛工況數據庫。

每類行駛工況的道路實驗分別采集6 000組數據，每組數據時長為1 s。對采集的數據進行預處理，對于個別缺失的數據利用插值方法補全，對于產生的奇異值作刪除處理，處理后的各典型行駛工況數據見圖2。

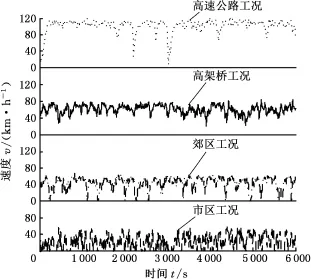
圖2 典型行駛工況實驗數據Fig.2 Experimental data of typical driving cycle

2.2 樣本抽取

為使樣本數量充足，保證識別精度，采用隨機數法抽取工況樣本，具體方法見圖3。抽取的樣本數據80組，每組數據時長為1 s，即識別周期為80 s。

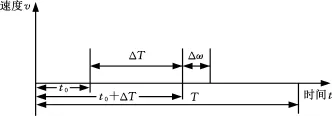
圖3 樣本抽取Fig.3 Sample extraction

圖3中，ΔT為識別周期；Δω為更新周期；T為該類行駛工況數據總量；t0為樣本抽取的起始時刻。每類行駛工況抽取400個樣本，共計1 600個樣本，抽取的樣本起始時刻的表達式如下：

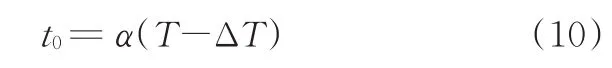
式中，α為產生的隨機數，α∈（0，1）。

2.3 樣本特征分析

若要保證行駛工況識別的準確性，需確定足夠且有效的工況識別輸入參數，全面統計和分析工況特征，尤其市區工況行駛速度波動大，經常出現走走停停的狀況，因此特征參數既要反映車輛運行快慢特性，又要反映速度波動特性。根據文獻［1，17］，本文定義14個特征參數描述各工況樣本，見表1。

利用MATLAB編程分別求出各典型工況樣本的特征參數值，得到樣本數量n（行）×特征參數m（列）的矩陣，并按下式進行歸一化處理：

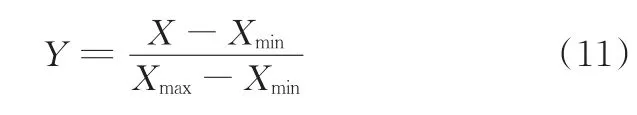
式中，Xmax、Xmin分別為樣本數據X的最大值和最小值。

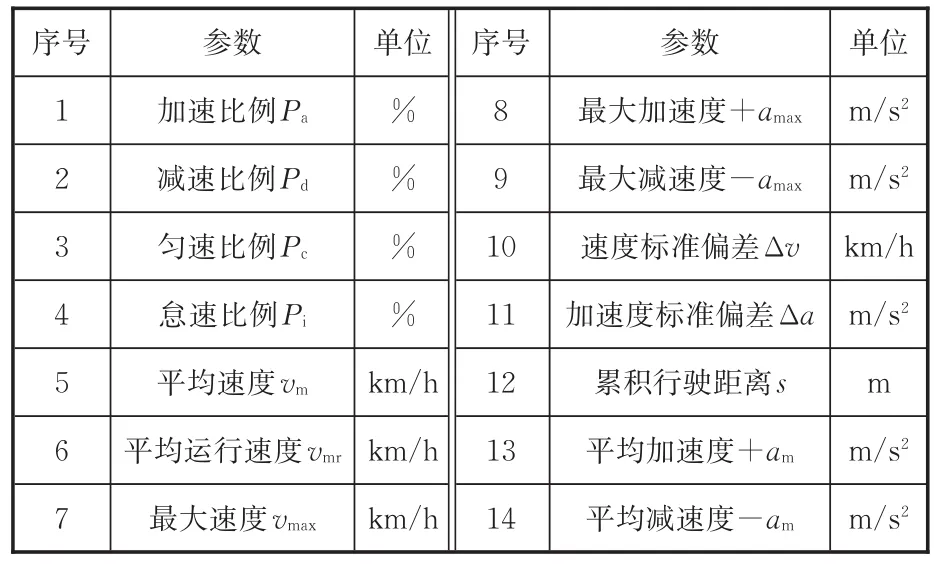
表1 行駛工況特征參數Tab.1 Characteristic parameters of driving cycle

定義的14個特征參數之間存在相關性，會對識別模型造成負面干擾，降低識別精度。而主成分分析能夠很好地克服參數間的相關性，把多個指標轉化為幾個綜合指標，因此對典型工況樣本的特征參數應用主成分分析，得到14個主成分（用Mn表示，n=1，2，…，14）。各主成分的貢獻率和累積貢獻率見表2。通常選取累計貢獻率達到80%以上時所對應的主成分代表所有原始變量進行分析。同時若主成分的特征值小于或等于1，說明該主成分包含的信息量少于或等于直接引入1個原變量的信息量，故選用主成分時，一般要求特征值大于1。由表2可以看出，前3個主成分的特征值均大于1且累積貢獻率達到了84.772%，因此選取前3個主成分作為PSO-SVM識別算法的輸入參數。各典型工況樣本前3個主成分得分見圖4。

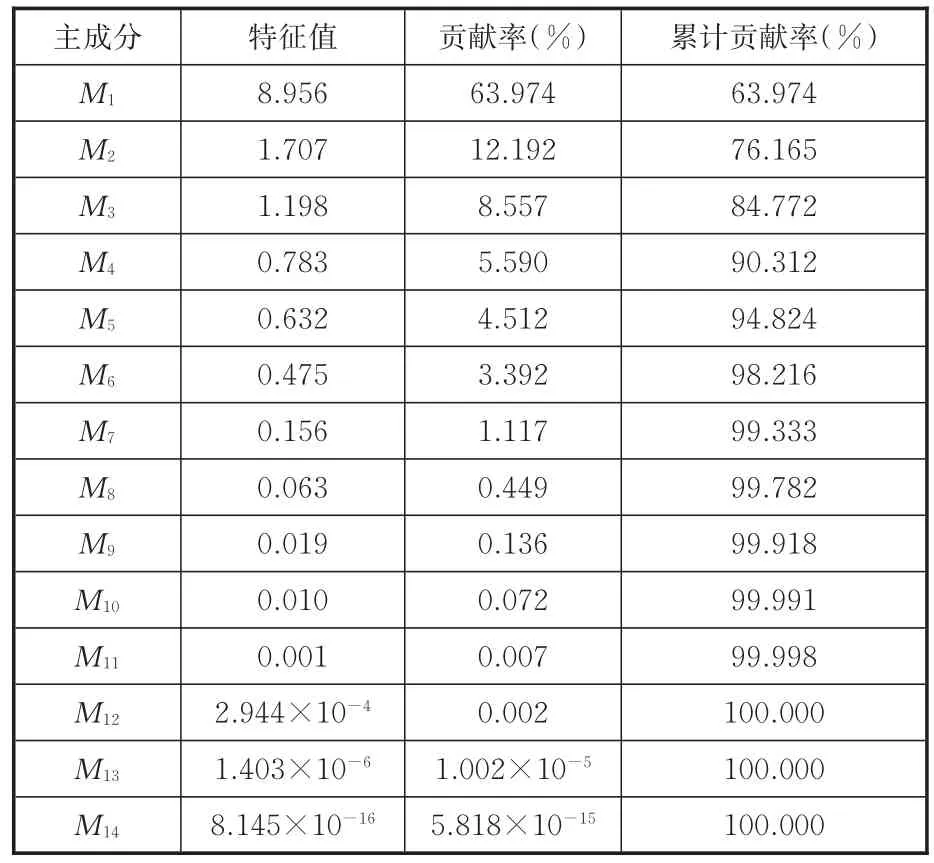
表2 各主成分貢獻率和累積貢獻率Tab.2 The contribution rate and cumulative contribution rate of principal component

2.4 基于PSO-SVM算法的行駛工況識別模型

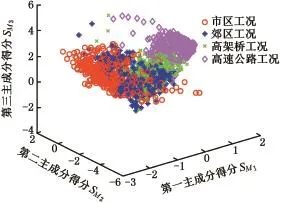
圖4 各典型工況樣本主成分得分Fig.4 The principal component scores of typical driving cycle sample

上述3個主成分作為PSO-SVM算法的輸入參數。從1 600個主成分得分樣本中隨機抽取80%作為訓練樣本，建立識別模型；剩下20%作為測試樣本，驗證識別模型的精度。粒子群算法種群規模設置為20，最大迭代次數為100。將基于PSO-SVM算法和基于k-cv交叉驗證法建立的SVM識別算法進行比較，以評價PSO優化后的識別效果。k-cv交叉驗證法中將C、g分別取以2為底的指數離散值，即 C∈{2-10，2-9，…，29，210}，g∈{2-10，2-9，…，29，210}，進行網格尋優，分別取識別精度最高時所對應的C、g值作為最優值。PSOSVM算法的迭代過程和k-cv交叉驗證法尋優過程分別見圖5和圖6。

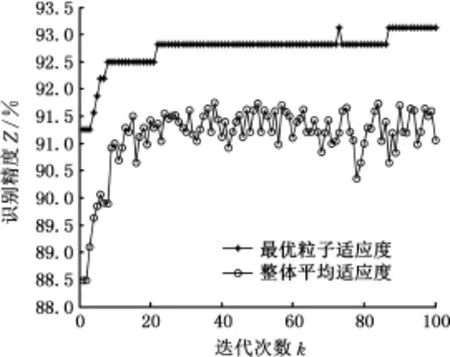
圖5 PSO-SVM算法的迭代過程Fig.5 The iteration process of PSO-SVM algorithm

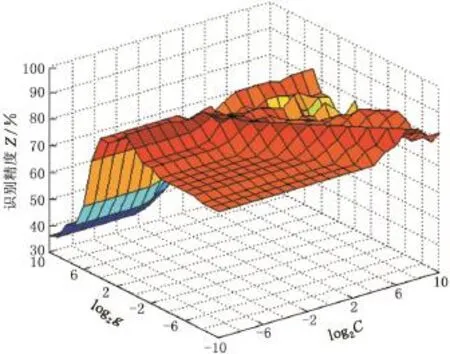
圖6 k-cv交叉驗證法尋優過程Fig.6 The optimization process of cross validation based on k-cv

由圖5可以看出，經過100次迭代，PSO-SVM算法尋得最優粒子時的識別精度為93.125%，對應的最優粒子C=4.433，g=7.126。而k-cv交叉驗證法識別精度最高為88.994%，對應的最優粒子C=0.25，g=16。由此可見，基于PSO-SVM算法的行駛工況識別精度提高了4.131%。兩種算法的320個測試樣本的識別結果見圖7，可以看出，兩種情形下，高速公路工況的識別錯誤率最低，郊區工況的識別錯誤率最高。而基于PSOSVM算法建立的識別模型在市區、郊區和高架橋工況的識別精度均高于k-cv交叉驗證法的識別精度，而在高速公路工況下，2種算法的識別精度接近。

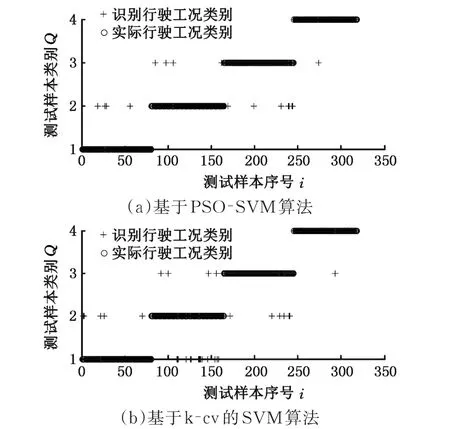
圖7 測試樣本識別結果Fig.7 Test sample recognition results

3 識別周期及更新周期對行駛工況識別精度的影響分析

在識別模型的建立過程和在線應用中，識別周期ΔT和更新周期Δω存在不確定性。ΔT的大小決定樣本數據時長，進而決定樣本所含信息量，ΔT過小，獲得的工況信息量較少，可信度降低；ΔT過大，無用的信息增多，不利于反映參數特征。而Δω的大小決定工況信息更新的快慢，Δω過小，則計算量增加，對處理器要求提高，且可能導致識別的工況頻繁切換；Δω過大，則工況識別的靈敏度降低，不利于實時最優控制。由此可知，選取合適的識別周期和更新周期是準確識別工況的保證。本文分別選取ΔT=30 s、80 s、130 s、180 s抽取樣本，應用PSO-SVM識別算法和基于k-cv交叉驗證法的SVM識別算法建立識別模型，并以一段隨機組合行駛工況為例，分別考慮Δω=5 s、10 s、20 s時，對隨機工況進行實時在線識別，比較識別結果，并確定最優ΔT和Δω，隨機行駛工況見圖8。篇幅限制，只列舉了ΔT=80 s、Δω=10 s時的情況，2種算法在線識別結果見圖9。根據式（7）對識別結果進行統計，其中PSO-SVM算法的識別精度達到了91.089%，而基于k-cv的SVM算法的識別精度為83.168%，PSO-SVM算法的精度提高了7.921%。

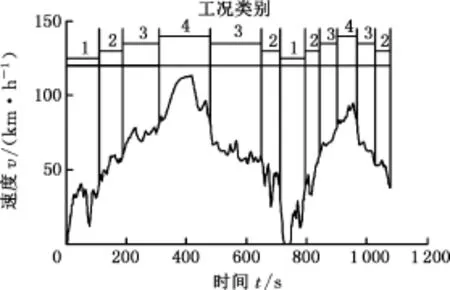
圖8 隨機行駛工況Fig.8 Random driving cycle

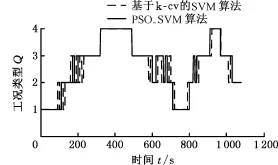
圖9 在Δ T=80 s、Δ ω=10 s時的在線識別結果Fig.9 Online recognition results when ΔT=80 s，Δ ω=10 s

通過一系列重復交叉試驗來獲取最優ΔT和Δω，2種算法下所有組合在線識別結果見圖10和圖11，可以看出，PSO-SVM識別算法的精度普遍高于基于k-cv的SVM識別算法的精度。ΔT增大時，PSO-SVM算法的識別精度均有所提高，但當ΔT進一步增大時，PSO-SVM算法的識別精度有下降的趨勢，這也符合前文提及的識別周期過小或過大均不利于實時在線識別的分析。當ΔT=30 s和180 s時，2種算法的識別精度均隨Δω的增大而降低；當ΔT=80 s和130 s時，PSO-SVM算法的Δω取中間值10 s時，識別精度最高。綜合以上分析，在ΔT=80 s、Δω=10 s時，PSO-SVM算法的識別精度達到90%以上，可依據此確定ΔT和Δω數值。

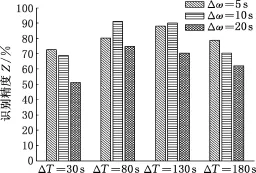
圖10 PSO-SVM算法在線識別精度Fig.10 PSO-SVM algorithm online recognition results

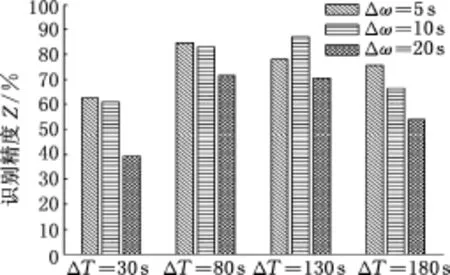
圖11 基于k-cv的SVM算法在線識別精度Fig.11 SVM algorithm online recognition results based on k-cv

4 行駛工況識別在混合動力汽車能量管理策略的應用分析

4.1 基于行駛工況識別的能量管理策略

行駛工況對混合動力汽車的燃油經濟性有較大的影響［1］，因此為進一步提高整車燃油經濟性，能量管理策略應根據當前行駛工況的特點，實時調整策略控制參數值，以實現不同動力源功率分配的實時最優。等效燃油消耗最小策略（equivalent fuel consumption minimization strategy，ECMS）具有結構簡單、運算量小、無需先驗知識的優點，且通過引入懲罰函數，使得該策略具有良好的電量保持特性，可較好地適用于插電式混合動力汽車的電量保持階段的能量管理，因此被廣泛研究［18-19］。

ECMS控制思想是：根據整車的實際駕駛員需求功率，在發動機和電機的功率范圍內合理分配發動機和電機的實際輸出功率，使得發動機瞬時燃油消耗率和電機消耗電量的等效燃油消耗率的總和最小，即

綜上所述，若要將行駛工況識別應用到ECMS中，需提前獲得各典型工況下ECMS最優充電等效因子和放電等效因子。針對以上問題，以降低燃油消耗量為優化目標，建立基于P2構型的某插電式混合動力汽車Simulink模型，整車構型見圖12，整車及能量管理策略頂層Simulink模塊見圖13，動力及傳動系統參數見表3。

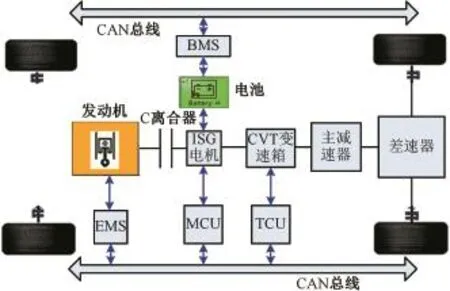
圖12 某插電式混合動力汽車整車構型Fig.12 Configuration of a plug-in hybrid electric vehicle

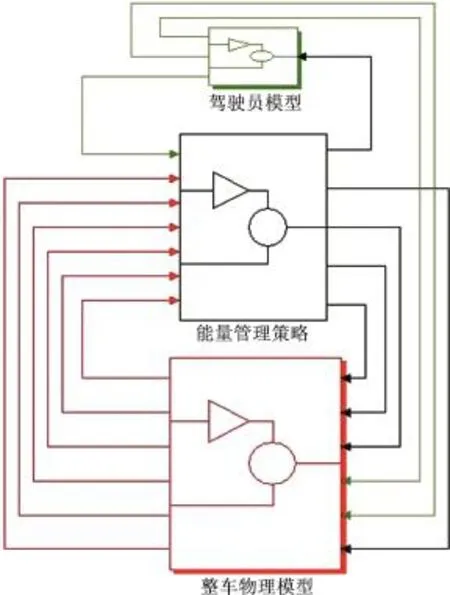
圖13 整車及能量管理策略頂層模塊Fig.13 Top-level module of vehicle and energy management strategy

利用Simulink模型描述充放電等效因子與目標參數之間的非線性關系，并采用智能優化算法獲得各典型工況及綜合工況下ECMS最優充電等效因子和放電等效因子，見表4。

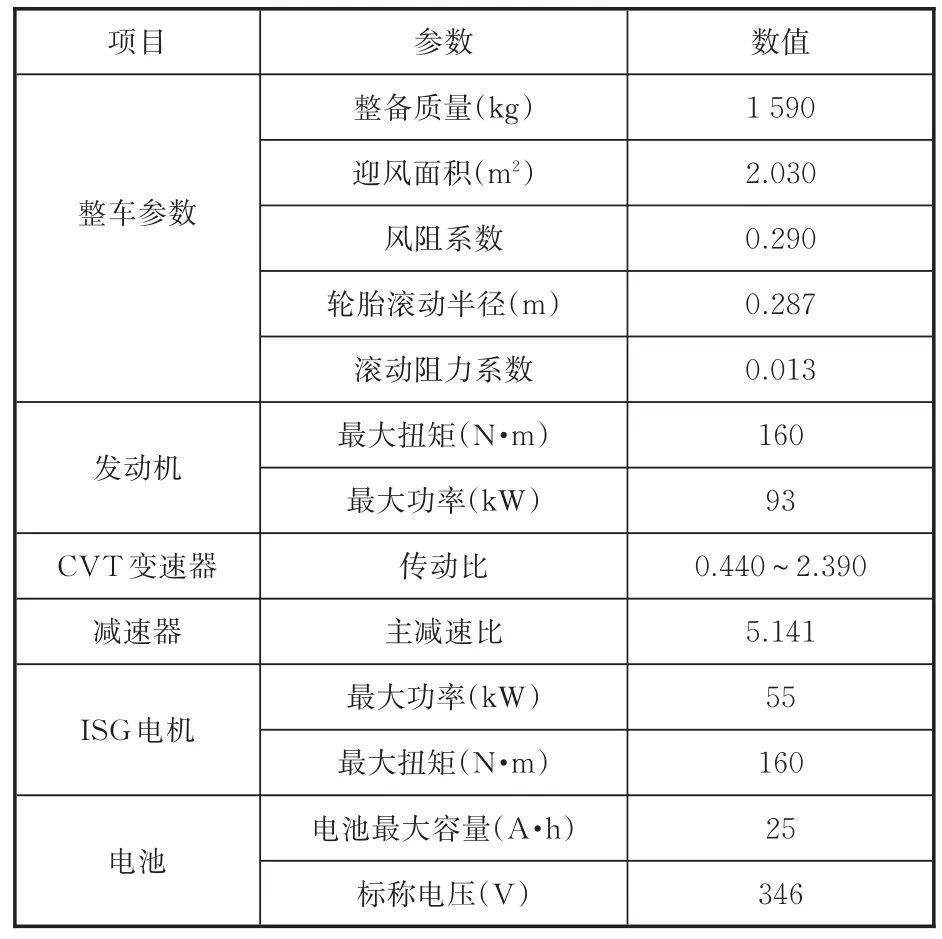
表3 動力及傳動系統參數Tab.3 Power and transmission system parameters

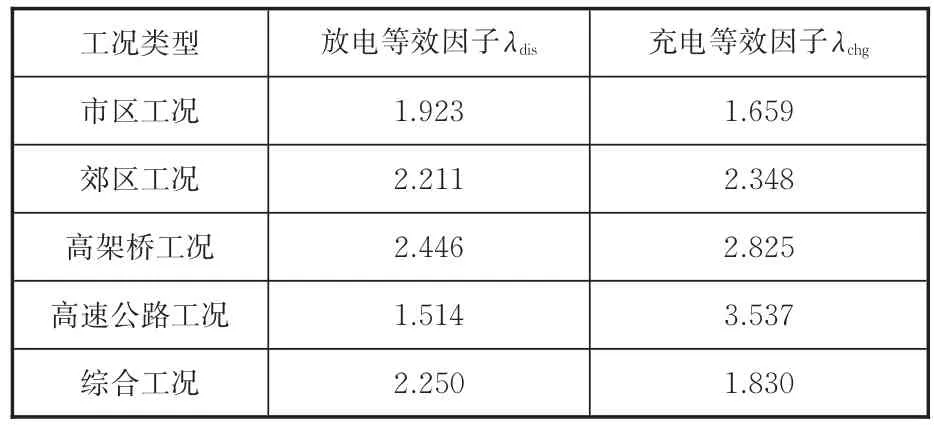
表4 各典型工況最佳充放電等效因子Tab.4 The optimal charge and discharge equivalent factor in the typical driving cycle

4.2 基于行駛工況識別的ECMS仿真分析

為了對比分析，考慮3種情形，即未采用行駛工況識別的ECMS、基于k-cv的SVM行駛工況識別的ECMS及基于PSO-SVM算法行駛工況識別的ECMS（簡稱為模式一、模式二和模式三）。將隨機行駛工況在ΔT=80 s、Δω=10 s時的各識別結果序列導入Simulink整車模型中的能量管理策略模塊內，利用Switch模塊切換充放電等效因子數值。仿真整車在電量保持階段的性能，初始SOC值設定為0.63，電池SOC值上下限分別為0.7和0.6。仿真過程車速跟隨情況見圖14，可以看出，3種模式下的ECMS均滿足車輛需求功率，實際車速與目標車速基本吻合，車速跟隨誤差較小。

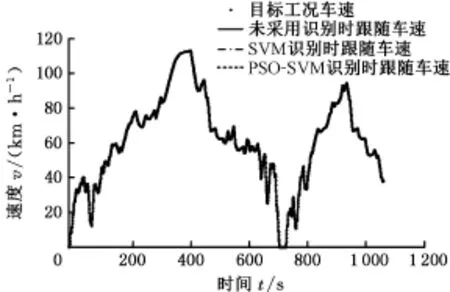
圖14 車速跟隨情況Fig.14 Velocity following condition

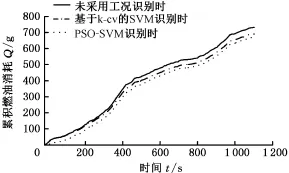
圖15 累積燃油消耗量Fig.15 Cumulative fuel consumption

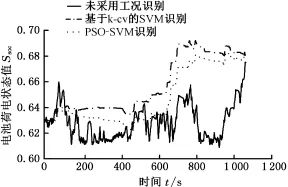
圖16 SOC變化曲線Fig.16 The curves of SOC

模式一～模式三時的累積燃油消耗量和SOC變化曲線分別見圖15和圖16。分析圖15可知，模式一時策略累積燃油消耗量為732 g，百公里油耗為5.343 L；模式二時策略累積燃油消耗量為690 g，百公里油耗為5.042 L，相對于模式一，燃油經濟性提高了5.634%；模式三時策略累積燃油消耗量為660 g，百公里油耗為4.817 L，相對于模式一，燃油經濟性提高了9.836%，而相對于模式二亦提高了4.348%。電池荷電狀態（SOC）用參數Ssoc表示，其數值表示剩余電量占比，1表示電池充滿電，0表示電池放完電。由圖16可知，3種模式下的SOC保持性能均較好，與目標SOC值偏差均在5%以內，但模式一時的電池SOC波動較大，充放電次數較多。模式二與模式三時的SOC變化相對平穩，且電池充放電次數減少，有利于提高系統效率和延長電池壽命。

5 結論

（1）分析了合肥市交通特征與道路特征，分別在代表市區工況、郊區工況、高架橋工況和高速公路工況的道路進行實車實驗，采集大量行駛工況數據。定義了描述行駛工況特性的特征參數，利用多元統計理論對數據進行了處理，提取出可用于行駛工況識別的參數。

（2）建立基于粒子群優化的SVM識別算法，并通過實例分析可知，PSO-SVM算法識別精度比基于k-cv交叉驗證法的SVM算法的識別精度高。討論了行駛工況識別過程中，識別周期和更新周期對識別精度的影響，結果表明在識別周期為80 s、更新周期為10 s時，識別精度最高，但仍需進一步提高。

（3）將行駛工況識別技術應用到插電式混合動力汽車的能量管理策略中。仿真結果表明，相對于未采用行駛工況識別及基于k-cv交叉驗證法的SVM識別，PSO-SVM算法可有效提高整車燃油經濟性，且電池SOC的波動相對平穩，可提高系統效率。