指數和線性參數化的輪胎-路面縱向附著條件實時估計方法

熊 喆 過學迅 裴曉飛 張 杰

1.武漢理工大學現代汽車零部件技術湖北省重點實驗室，武漢，430070 2.萬向集團技術中心，杭州，311200

0 引言

輪胎-路面的縱向附著特性通常由以車輪滑移率λ為橫坐標、附著系數μ為縱坐標的μ-λ曲線表示，曲線呈非線性且包含單一極大值。該極大值對應的縱坐標為輪胎可利用的峰值附著系數μp，橫坐標為最優滑移率λp。峰值附著系數為自適應巡航控制（ACC）、駕駛輔助系統（ADAS）和再生制動分配控制等功能提供必要信息，最優滑移率則是防抱死制動系統（ABS）縮短制動距離的關鍵控制目標。在車輛主動安全的研究領域，在各種提高車輛穩定性和縮短制動距離的先進控制方法中，大多以該峰值點已知為必要條件，因此峰值點的估計方法一直是研究熱點之一。

輪胎-路面附著特性估算方法大致分為兩類，即基于原因（cause-based）和基于結果（effectbased）［1］。由車輛參數響應和數學模型反向推導附著特性是基于結果方法中的一種。相較于其他方法，這種方法無需加裝特殊傳感器，故常常成為主機廠的首選方法。一般認為，在小滑移率（≤5%）范圍，μ-λ曲線斜率值（縱滑剛度系數）與輪胎參數主要相關，與路面類型次要相關。在使用常規傳感器的條件下，小滑移率的輕度制動工況很難準確預測峰值附著系數及對應的最優滑移率［2］。通常的方法是對小滑移率工況下的μ-λ散點進行直線擬合，通過斜率值來大致區分高、低附著路面［3］。當出現較大滑移率的制動工況時，μ值會越過峰值點并進入非線性區域，此時需要引入合適的估計方法獲取峰值點坐標。本文提出一種指數和（exponential sums，ES）模型線性化的輪胎-路面縱向附著條件實時估計方法。

1 縱向制動過程的車輛參數響應

1.1 輪胎-路面縱向附著力

電動汽車的制動系統正以“線控”為發展方向，無論是電子液壓制動系統還是電子機械制動系統，配合再生制動系統，都具備制動力矩可測的特點，從而為附著條件的估計提供了很大幫助。此外，為最大化回收能量，許多再生制動分配策略［4］傾向于最大化地利用再生制動輪的附著系數，使得再生制動輪優先趨于抱死，以CarSim軟件內的E-class Sedan車身參數為例，繪制的典型制動分配線如圖1所示。圖中，z為制動強度。其中，最大化能量回收分配策略以I曲線（理想分配線）、f線組（前輪抱死線）和ECE法規線為參考線，規劃前后軸制動力分配線，表示為OABCD線段。其基本思想是：在保證車輪運行于線性穩定區間的前提下，盡可能將需求制動力分配給再生制動輪（此處為前輪）。OA線段所處的低強度制動工況下，需求制動力全部分配給前輪；AB曲線位于ECE曲線上方，垂直距離取決于設計者的余量系數；BC線段位于當前路面峰值附著系數對應的f線左側，距離也取決于余量系數。CD曲線與I曲線重合，此時前后輪有相近的滑移率和附著系數利用率。

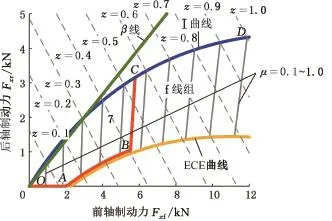
圖1 典型制動分配線Fig.1 Typical brake force distribution curves

明顯地，當路面附著系數對應的f線處于BC線左側時，重度制動情況下可能導致前輪抱死而后輪未能完全利用附著力的情況發生。理想方案是實時獲取路面附著條件并及時調整BC線段位置。本文以電動汽車前輪為具體分析對象，對輪胎-路面縱向附著力進行研究，研究中暫不考慮電機再生制動的功能。

附著系數μ的定義為

式中，Fx為車輪受到的縱向附著力；Fz為輪胎受到的法向載荷。

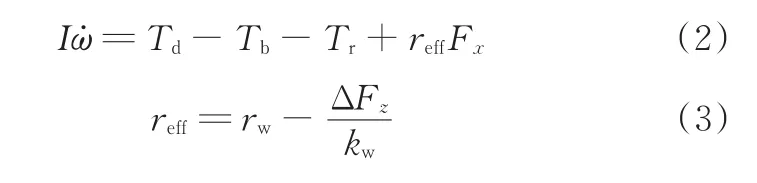
式中，I為車輪及聯動部件的合慣量；ω為輪速；Td為車輪所受驅動力矩；Tb為制動器提供的力矩；Tr為滾阻偶矩；reff為車輪有效滾動半徑；rw為車輪靜態負載半徑；kw為輪胎彈簧剛度。

由車輛縱向運動時車輪的力矩平衡可得

對于燃油車輛，制動過程中的驅動力矩難以估計，式（2）作了視驅動力矩為零的過度簡化處理。該簡化的缺陷在于，無論處于AT（自動變速器）或MT（手動變速器）掛擋狀態下的制動，驅動力矩對車輪運動都會有一定的影響，尤其在低附著系數路面，忽略驅動力矩將對附著條件估計帶來顯著的誤差。若不考慮式（2）中的驅動力矩，由CarSim輸出值計算的估計結果如圖2所示，估計值與真值有著較大的偏差。

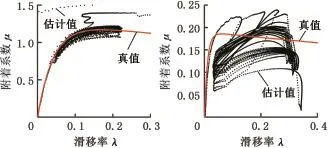
圖2 燃油汽車的附著條件估計結果（不考慮驅動力矩）Fig.2 Estimated results of adhesion of a fuel vehicle（without considering drive torque）

對于傳動系統結構簡單的電動車輛，驅動/再生制動力矩值可由電機ECU直接提供，從而有效降低因驅動力矩估計不準導致的誤差，因此電動車的優勢也體現在：使用式（2）的簡單模型依然能夠得到準確度較高的附著力估計值。

1.2 滾阻偶矩

滾動阻力系數的精確值通常由轉鼓試驗獲得，或由滑行試驗獲得滾阻風阻系數［5］。考慮到大滑移率制動工況下的滾阻占比較小，此處視系數為已知，則滾阻偶矩表示為

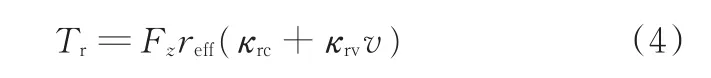
式中，κrc、κrv分別為滾動阻力系數的常數系數和速度系數，取 4×10-3和 2.5×10-5。

1.3 車輪載荷估計

假設車輛行駛于平坦硬路面，且車輛重心位于xy平面的中軸線上。通過求解制動時前后軸載荷力和力矩平衡方程可得左前輪載荷Fz_L1的簡化估計表達式：

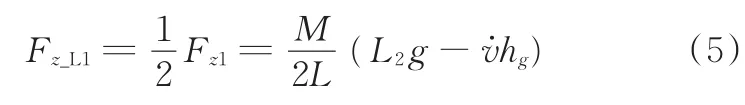
式中，M為整車質量；g為重力加速度；Fz1為前軸載荷；hg為車輛重心高度；L為軸距；L2為重心至后軸的水平距離。

變量M、L2、hg會隨車輛負載狀態而改變，此處假設變量可由相關估計方法獲得［6］，并在后文的仿真和試驗中視之為恒定參數。

1.4 滑移率計算

制動工況下的瞬時滑移率定義為

當滾動的充氣輪胎的某一系統變量（側偏角、外傾角或縱向滑移率）發生變化時，輪胎進入一種非平衡狀態，側向和縱向附著力都會經歷一次短暫的改變，直至從非平衡狀態過渡至平衡態［7］。因為輪胎的偏轉或形變需要一定時間，隨后才能達到穩態條件。

縱向附著條件由載荷、滑移率和縱向力三個變量決定。其中，載荷不受輪胎弛豫現象的影響；瞬時滑移率由傳感器信號及相應算法估計獲得，得到的是一個針對輪轂而非輪胎的非弛豫值；縱向附著力的估計是從車輪動力學的角度出發，由車輪運動反推，因而得到的是一個弛豫值。在建立滑移率與輪胎摩擦力的模型時，應考慮弛豫現象并進行時域統一。輪胎弛豫模型的滑移率表示為［8］

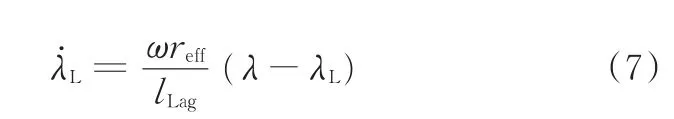
式中，λL為弛豫滑移率；lLag為輪胎弛豫長度，取55 mm。

1.5 ABS控制器

ABS控制器結構種類繁多，為不失一般性，本文的仿真試驗使用常規有限狀態機（FSM）ABS控制器，其控制邏輯如圖3所示。圖中，q為狀態編號；Tbmin、Tbmax、λmin、λmax分別為μ-λ平面上4個自定義滑模面；U代表ABS控制器信號對應的EHB制動力矩增壓、減壓、保壓速率，kin、kde分別為增壓、減壓速率值，由文獻［9］獲得。

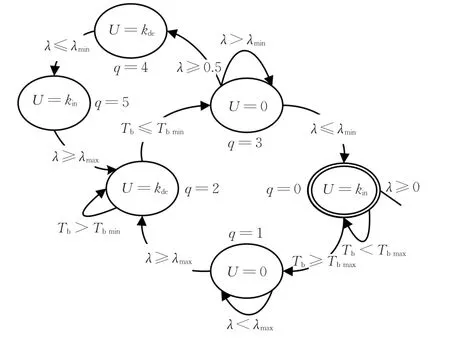
圖3 離散有限狀態機ABS控制器Fig.3 FSM ABS controller

2 附著特性曲線辨識

2.1 Burckhardt模型

Burckhardt摩擦模型的準靜態形式僅含3個系數，是表達輪胎-路面附著特性的經驗模型之一，其表達式為

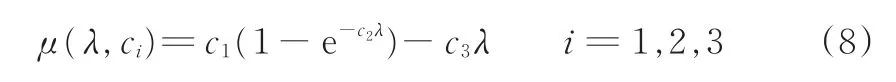
式中，c1、c2、c3為擬合系數。

典型路面的系數值如表1所示。

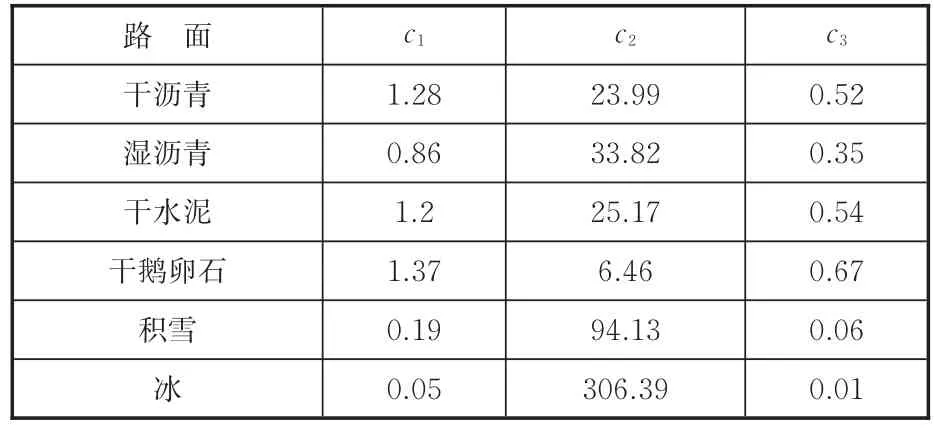
表1 Burckhardt模型典型路面系數Tab.1 Coefficients of Burckhardt model

需要指出的是，Burckhardt模型能夠表達無數種附著條件，包括但不限于表1中所列的6種路面。由式（8）可知，該模型僅對路面進行了描述，對于輪胎-路面附著特性的另一要素“輪胎”則未涵蓋。這也是該模型與魔術公式的主要區別之一。即使是在同一種路面，在溫度、輪胎（胎寬、胎壓、紋路等）、外傾角等參數變化的情況下，曲線形狀和擬合系數仍有發生較大變化的可能（例如，F1賽車使用的熱熔胎在干瀝青路面可獲得大于2的峰值附著系數）。另一個重點是，Burckhardt模型包含一個指數非線性項e-c2λ，難以設計出符合本文實時性要求的非線性擬合算法。最合適的解決方案是設計合理的線性化近似，再以計算量較小的最小二乘擬合算法進行辨識。

2.2 Kiencke線性化

Kiencke［10］提出了一種針對 Burckhardt模型的線性化方法，該線性化方法的前提是，假設所有路面特性曲線的初始斜率μ′(0)為一個定值，則Burckhardt模型可近似線性化為

式中，a1、a2為待估參數。

令一個中間變量y(t)=μ′(0)λ(t)-μ(t)，則有：

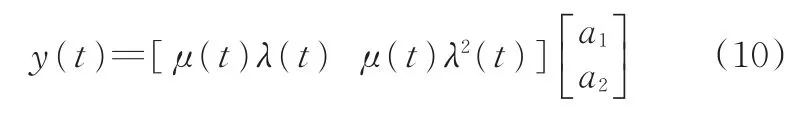
那么類似地，可用遺忘因子遞推最小二乘方法辨識參數a1、a2，式（10）可表示為

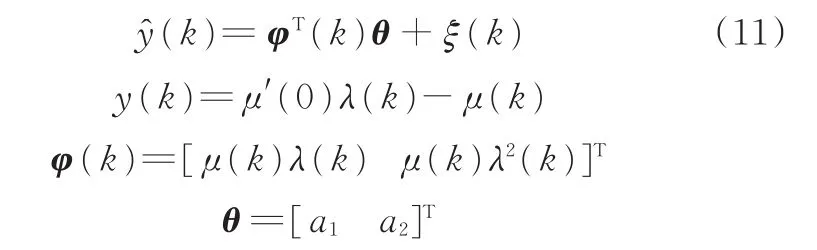
式中，ξ為噪聲。

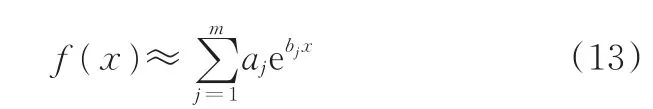
式中，aj（j=1，2，…，m）為待估系數,aj∈R；bj為預設參數，bj∈ R。

當確定函數定義域，并根據函數性質和誤差要求給定m值和bj時，可將非線性函數近似線性化。需要指出的是，由于式（12）中的非線性項-c1e-c2λ已經是指數形式，因此指數和模型對該項有較好的逼近效果［11］。將式（13）模型結構替換式（12）的非線性項，并利用μ(λ)曲線始于坐標原點的性質，即令μ（0）=0，從而式（12）可表示為

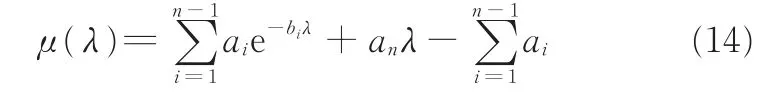
由一階偏微分小于0和二階偏微分等于0兩個條件求解得到極大值點縱橫坐標（即最優滑移率、附著系數峰值）分別為

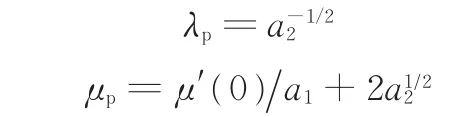
Keincke模型中的初始斜率μ′(0)為縱滑剛度。縱滑剛度一般只與輪胎參數相關，與路面條件無關，因此該模型的缺點在于，當輪胎參數發生改變，準確性會顯著降低。

2.3 指數和線性化方法

式（8）展開：

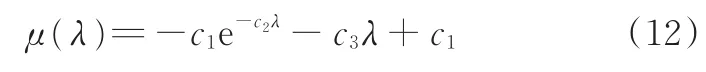
指數和線性化屬于非線性逼近理論的方法之一，對于某非線性函數f(x)，其指數和逼近模型為

式中，ai為待估系數，i=1，2，…，n；bi為預設參數，i=1，2，…，n-1。

從而辨識模型表示為

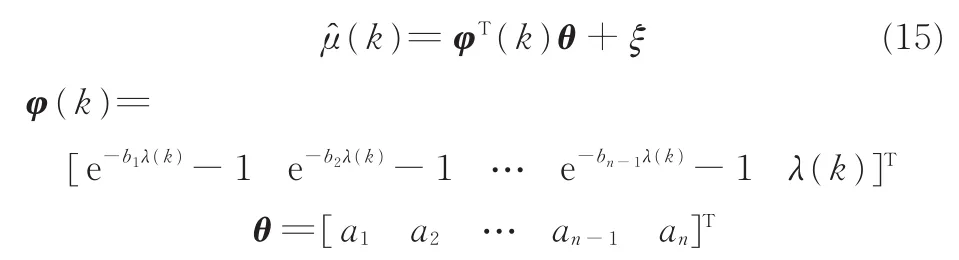
在利用最小二乘辨識算法得到θ值后，對式（14）進行一階和二階偏微分，則極大值點μp(λp)為以下方程的解：

考慮到參數bi用于擬合c2，此處參考標準Burckhardt模型中的c2值作為bi的取值范圍，排除冰面路段c2=300的極端情況，取 bi∈［1，100］。考慮到擬合參數的數量過多，會導致計算量增多，數量過少則導致擬合精度降低。為兼顧兩者，此處取n=5，取b1=4，b2=40，b3=70，b4=100。按此取值對標準Burckhardt模型曲線進行離線擬合，結果如表2所示，由和方差（SSE）結果可知擬合程度較高。進一步地，如表3所示，相較于其他使用指數和方法擬合的結果，本文方法經參數優化和結構簡化，在降低待估參數數量的同時，精確度也得到了提升。

由式（16）可知，與Burckhardt模型有極大值解析解不同，式（16）中一階微分方程的表達式雖為顯式，但為一個含高階指數多項式的超越方程，無法給出解析解，只能求數值解。由于對λp解的精度要求不高，故求解步長取0.001即可，同時以μ(0)=0為初值，0～0.5為 λp范圍。對于基于MATLAB的仿真而言，可用的求解方法包括：①使用fsolve函數對式（16）所示的一階微分方程求取數值解；②使用findpeaks函數獲取如式（14）所示曲線的極大值坐標，輸出結果為函數極大值點的縱橫坐標對應的兩組向量，向量長度取決于極大值點的數量。在本文仿真中，使用了上述第二種方法編寫求解程序，當解出多個極大值點時，取橫坐標最靠近0的解，函數框架表示為

表2 Burckhardt模型的指數和線性化擬合結果Tab.2 Fitting results of Burckhardt models by ES linear parameterization

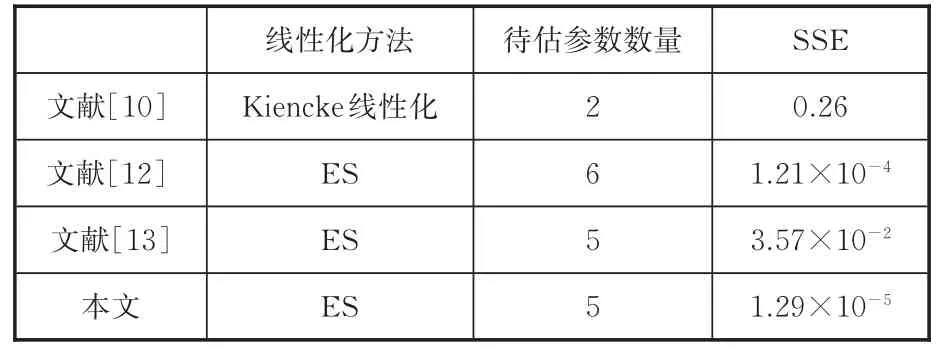
表3 兩種線性化方法的擬合結果對比（濕瀝青）Tab.3 Contrast of linear methods（wet asphalt）

2.4 遺忘因子遞推最小二乘（FFRLS）算法

采用遺忘因子最小二乘算法，遞推公式為

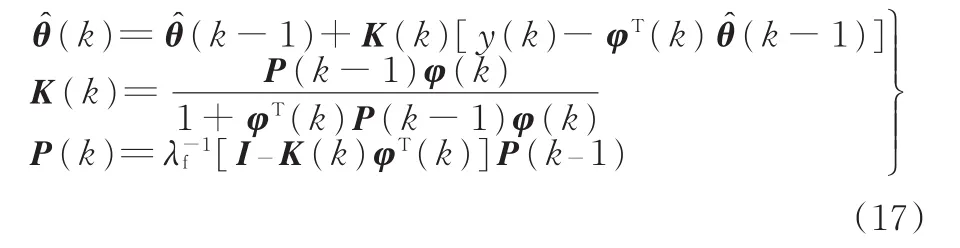
設置初始化參數P(0)=10I，在本文中，I為5階單位陣。參數初值?(0)和遺忘因子λf的取值將于仿真試驗部分討論。

3 仿真與硬件在環（HiL）試驗

基于前文所述思路，搭建了基于MATLAB/Simulink和CarSim的聯合仿真平臺。Simulink內的數據流如圖4所示，其中，i=L1,R1,L2,R2，分別指前軸左右車輪和后軸左右車輪。CarSim模塊包含整車參數、制動器參數和路面參數的設置，除此之外，包括制動器液壓模型、各參數估計算法、擬合算法和極大值求解算法在內的模塊均在Simulink中編寫。為更接近真實車輛，對估計的μ和λL結果加入白噪聲，取=0.012，=0.0022。

分步式硬件在環試驗用于驗證該算法的實時性。CarSim仿真得到的制動過程各參數，以離線數據的形式發送至作為虛擬估計器的dSPACE，流程如圖5所示。dSPACE返回的估計結果與仿真估計結果相同，但與仿真的較長耗時相比，HiL試驗達到了實時性的要求。

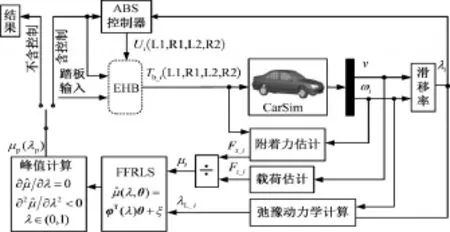
圖4 聯合仿真的計算框架Fig.4 Diagram of co-simulation

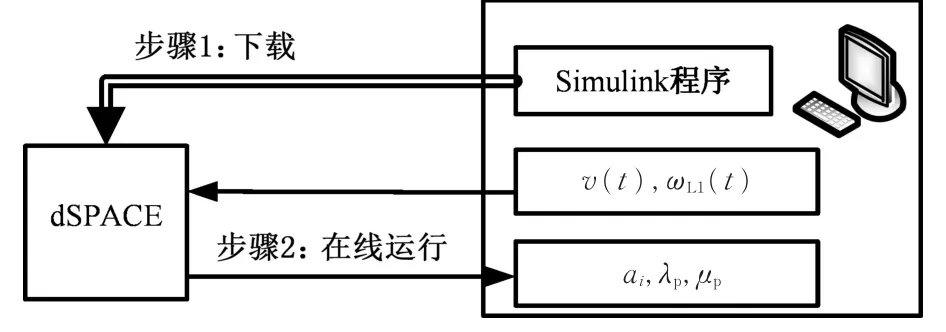
圖5 硬件在環試驗框架Fig.5 Diagram of HiL

3.1 單一路面試驗

本節所述仿真試驗的目的在于測試不同識別參數下的單一路面的識別結果，通過比較結果進而分析、優化?(0)和λf取值。

θ?(0)的取值分為兩種情況，第一種情況是在車輛點火（控制器初始化）時，由設計者預設一個初值，該值會影響第一次估計的速度。第二種情況是行車過程中，基于小滑移率工況下的散點統計斜率估計法的結果，這種情況下無論是高/低附著系數初值進入低/高附著系數路面，都將考驗估計器應對路面變化時的穩定性和收斂速度。

設初始為低附著系數路面（濕瀝青），并在高附著系數路面進行制動。取表2的離線擬合數據，峰值點縱橫坐標的估計結果如圖6所示。明顯地，當λf=0.95時，無論是μp還是λp的估計結果都出現了劇烈的振蕩，說明該遺忘因子值下的遺忘速度過快，參數和解的變化更劇烈，一旦峰值點橫坐標大于1，則返回(μp,λp)=(0,0)，由圖可知0.2～0.4 s處出現了多次無解的情況。在其余λf取值下的μp均能進入小誤差范圍，但λf取值過大，可能會導致λp的估計速度過慢。

設初始為高附著系數路面（干瀝青），并在低附著系數路面進行制動。取表2中的離線擬合數據，峰值點縱橫坐標的估計結果如圖7所示。由圖7可知，μp和λp的估計結果均能在第一個ABS增減壓循環內進入小誤差范圍，區別僅在于不同λf導致不同的估計速度和振蕩幅度。

圖6 低附著系數初值在高附著系數路面制動的估計結果Fig.6 Estimated results of braking on large adhesion road with small initial value

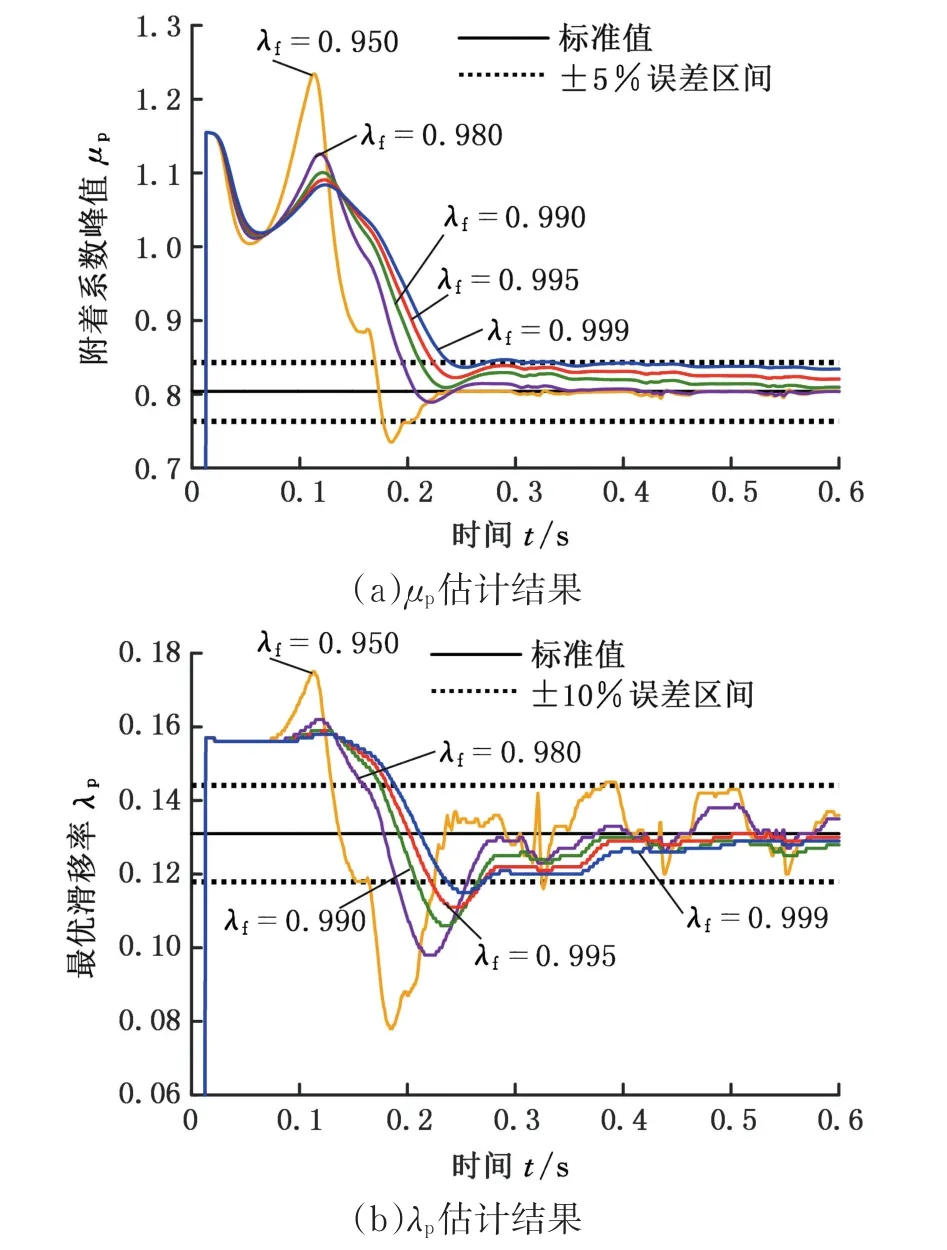
圖7 高附著系數初值在低附著系數路面制動的估計結果Fig.7 Estimated results of braking on small adhesion road with large initial value

由分析可得出參數選擇的結論：①在1 kHz的采樣頻率下，λf∈[0.980,0.995]的范圍能兼顧估計的收斂速度和準確度；②初值向量θ?(0)的取值在一定程度上影響著估計器的魯棒性。一般地，從高附著系數初值進入低附著系數路面，估計的結果會更加迅速和準確，將高附著系數初值作為程序初始化的初值較為合適，也符合車輛大部分時間行駛于鋪裝路面的客觀條件。

3.2 對接路面試驗

本節通過一組對接路面下的ABS制動過程仿真，比較Kiencke線性化方法和指數和線性化方法的估計結果。

如圖8所示，在CarSim中構建了一個同時包含積雪、干、濕路面的對接路面。需要指出的是，受制于CarSim軟件路面定義功能的限制，無法在一次仿真中定義一個包含幾組任意形狀的路面附著條件曲線的對接路面，只能定義一種形狀的附著條件曲線，再以改變滑動摩擦因數μs(λ=1)的值的方式，定義不同路面。

此路面以CarSim內置輪胎庫的225/60 R18的缺省縱向附著條件為基礎曲線，分別設置三種路面滑動摩擦因數μs為0.76、0.2和0.52，并通過計算得到各自的峰值點縱橫坐標。

CarSim缺省路面附著條件的曲線形狀與Burckhardt模型的曲線稍有不同，從量化的角度解釋，原因在于缺省曲線從滑移率0至1方向，曲線斜率一直在變化，而Burckhardt模型則只是在較大的μ值附近才有明顯變化，曲線的兩端則近似為直線。這一差別也能考驗估計方法對不同形狀附著曲線的適應能力。

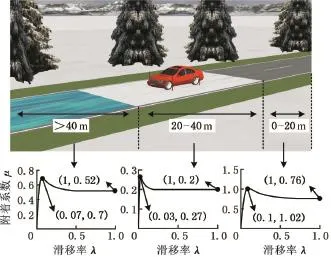
圖8 CarSim對接路面定義Fig.8 The customized road in CarSim

仿真的初始條件為，初始車速80 km/h，制動踏板迅速踩下，制動壓力從0 s開始上升，至0.3 s升至最大限壓值。如圖9所示，車輛在5 s內停止。這一過程中，估計的附著系數和弛豫滑移率的散點時間序列如圖10所示。

3.2.1 Kiencke線性化模型的估計結果

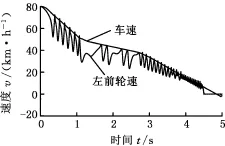
圖9 ABS制動過程中的車速與車輪線速度Fig.9 Vehicle speed and wheel speed during ABS condition

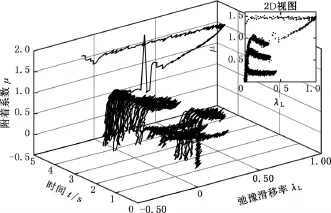
圖 10 估計μ?與λL的時間歷程Fig.10 Estimated results of?and λL

圖11 Kiencke模型的擬合曲線及其峰值點Fig.11 Fitted curves and their peak points（Kiencke）

μp的估計結果較準確，但在1～1.5 s處出現了峰形，其原因在于L1輪進入對接路面的瞬間，點(μ,λ)處于峰值右側的非線性區域，當制動力矩減小，該點從非線性區域逐漸退回線性區域的過程中，在遺忘因子的作用下，估計器結合之前高附著路面的散點(μ,λ)數據，擬合處的曲線的峰值點將往左上方移動，即μp增大，λp減小。在未展示的其他取值λf的仿真結果中，λf越小，該峰形的峰值點越大，且峰形之后會有持續小段時間的無解狀態（極大值點橫坐標λp大于1）。若λf逐漸增大，則峰形逐漸消失，但收斂速度將顯著降低，無法在短時間內進入小誤差區間。觀察圖12b可知，λp的估計結果較差，始終未能進入小誤差范圍。

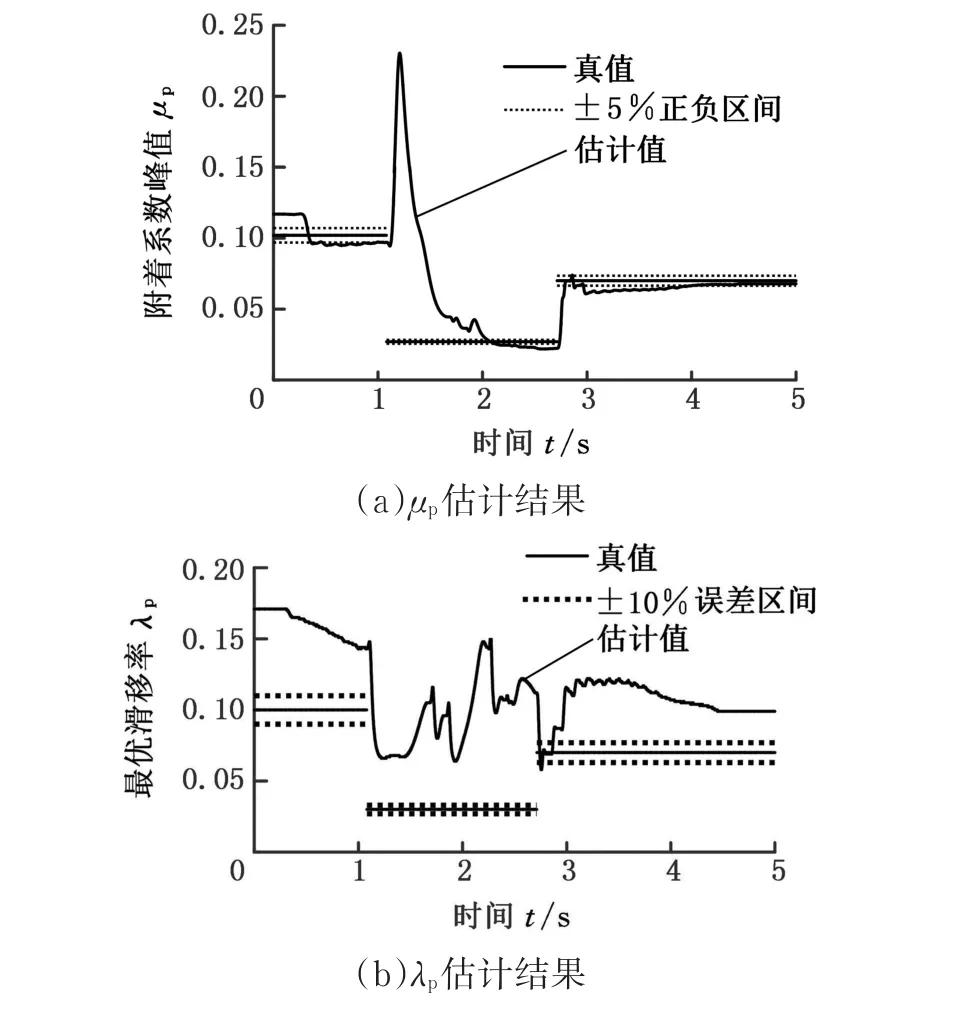
圖12 Kiencke模型峰值點坐標估計結果Fig.12 Estimated results ofμpand λp

3.2.2 指數和線性化模型的估計結果

設初值θ?(0)為指數和模型離線擬合Burckhardt干瀝青曲線的擬合結果，并取λf=0.995。圖13為該參數下的附著特性曲線及其峰值點估計結果，圖14a、圖14b為圖13中峰值點的兩個二維視角，分別為峰值點縱橫坐標的時間歷程。

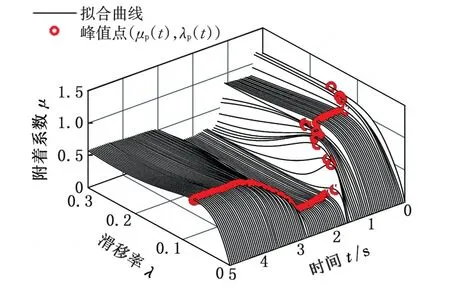
圖13 指數和模型的擬合曲線及其峰值點的時間歷程Fig.13 Fitted curves and their peak points（ES）

由圖14a可知，三種路面上的μp估計結果均非常精確，均能夠在0.5 s內進入小誤差區間，具體耗時的差別取決于制動器動態特性和滑移率狀態。在ABS作用下，由于制動力矩的動態特性T?b_L1不隨路面改變，當ω?L1＜ 0時，低附著路面的 ||ω?L1稍大于高附著路面，而當ω?L1＞0時， ||ω?L1則顯著小于高附著路面。那么當車輪經歷從高附著進入低附著的對接路面時，若點(μ,λ)處于非線性區域，則回到線性區域需要耗時更多，此情況會降低估計速度。即使這樣，估計方法仍然獲得了較好的估計結果，在1.1 s處進入低附著路面后的第一個ABS循環即進入了小誤差區間。同時，由圖14b可知，估計方法對λp的估計結果進入小誤差區間的耗時與圖14a近似，沒有出現大幅跳變的發散問題。

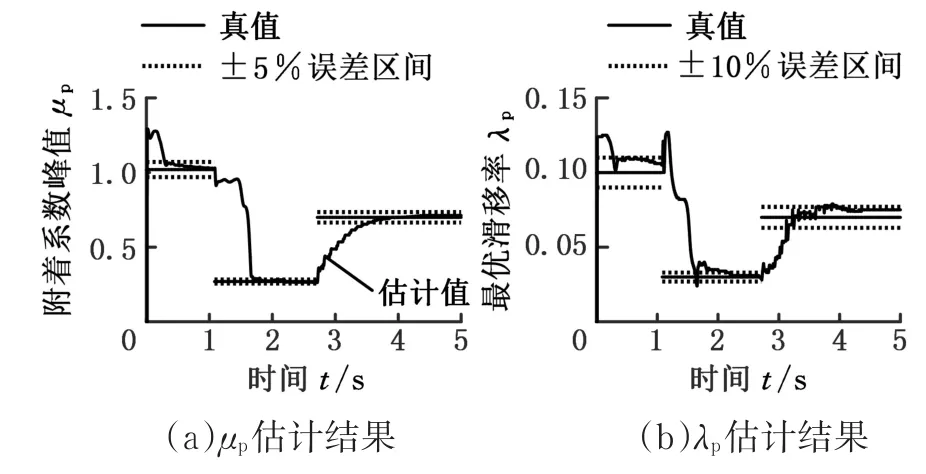
圖14 指數和模型峰值點坐標估計結果Fig.14 Estimated results ofμpand λp

4 結語

本文以前驅電動汽車的縱向制動工況為建模對象，研究了ABS觸發工況下的附著條件估計方法。方法基于Effect-based的估計思想，并通過指數和模型將Burckhardt非線性模型進行線性化，離線擬合數據證明該方法估計精度較高，可應用于任意車輛；設計和搭建了聯合仿真平臺和搭建硬件在環試驗平臺，硬件在環試驗驗證了實時在線估計的可行性，仿真平臺的結果表明，相較于Kiencke模型和其他指數和模型，本文設計的指數和模型的結構及參數具備更優的估計速度和精度，在大部分情況下，峰值點的縱橫坐標能于第一個ABS循環內進入±5%和±10%小誤差區間。