基于二階隱馬爾可夫模型的橋梁健康狀況分析與評定

葉 飛 ，盛昭瀚，徐 峰

（南京大學；1a.工程管理學院；1b.社會科學計算實驗中心，南京 210093；2.銅陵學院 信息技術與工程管理研究所，安徽 銅陵 244061）

橋梁是指為道路跨越天然或人工障礙物而修建的建筑物，是道路的重要組成部分，直接關系著行車和行人的安全，維系道路的安全與暢通，對于保障國家或地區社會經濟活動正常運行具有重要的作用[1]。中國作為發展中國家，在改革開放后開始步入大規模的橋梁建設階段。截至2013年底，全國公路橋梁達73.53萬座，總長3 977.80萬m，其中，特大橋梁3 075座，大橋67 677座，已超過美國躍居世界第一[2]。相對于發展中國家，美國等世界發達國家的橋梁建設高峰已過，大部分橋梁已經修建了較長時間。隨著時間的推移，無論是發展中國家還是發達國家，將有越來越多的橋梁進入老化階段，逐步成為危橋，直至引發橋梁安全事故。近十幾年來，國內外橋梁坍塌事故不斷。例如，1999年重慶綦江縣虹橋發生特大坍塌事故，導致40人死亡，14人受傷，造成直接經濟損失631萬元。2003年印度西部達曼市一座橋梁突然坍塌，正在橋上行駛的5輛機動車墜入河中，導致24人死亡，其中22人是小學生。2007年美國明尼蘇達州密西西比河大橋坍塌，導致8人死亡、79人受傷。這些橋梁坍塌事故造成了嚴重的人員傷亡，給國家財產造成了巨大的損失，并對社會經濟活動構成了嚴重的威脅。在這些橋梁坍塌事故中，很多是因為“年久失修或日常管護不到位”而引起的，都塌在建設或使用過程的管理上。為了保證橋梁安全和交通暢通，管理者需要及時發現橋梁發生的病害和出現的缺陷，及時了解橋梁的健康狀況，以便對橋梁進行科學、有效、及時地養護與管理。當前，橋梁的養護管理已引起了社會的廣泛關注，得到了政府、社會各界及人們的高度重視。

在橋梁的養護管理中，橋梁健康狀況的等級評定一般是依據橋梁定期的監測數據而進行的，通過對橋梁監測數據的綜合評定，確定健康狀況的等級，并對健康狀況的發展趨勢做出預測，進而制定橋梁的養護策略。其中，橋梁健康狀況的等級評定是至關重要的，等級評定的準確度直接關系到橋梁養護決策的質量。對橋梁健康狀況過高的估計會導致病害和缺陷不能被及時發現，從而增加橋梁的安全隱患，甚至引發橋梁安全事故；對橋梁健康狀況過低的估計會導致不必要的養護費用，從而增加橋梁的全生命周期成本，加重公共財政的壓力。橋梁本身作為一個復雜動態系統，具有隨機性和演化性。同時，監測數據也會存在一定的系統誤差和隨機誤差。在橋梁養護管理中，怎樣應對系統的隨機性、演化性和監測數據的測量誤差，提高橋梁健康狀況等級評定的準確度是管理者在進行橋梁養護管理決策時必須面對的問題。

近年來，馬爾可夫模型在管理決策中得到了日益廣泛的應用[3-4]。在橋梁的養護管理中，馬爾可夫模型也是一類重要的決策分析工具。究其原因，主要在于兩個方面：①因為馬爾可夫模型具有良好的數學結構，且便于使用；②因為馬爾可夫模型無須使用者對橋梁的工程原理和工程環境有徹底的了解[5]。在這類方法中，人們使用馬爾可夫過程來刻畫橋梁狀況的隨機性和演化性，通過一些離散的性能指標表示橋梁的健康程度，并通過馬爾可夫過程的狀態轉移概率表示健康狀況的退化趨勢和程度[6]。近年來，已有一些相關的研究見諸文獻。Lee[7]在有關橋面伸縮縫的研究中，利用馬爾可夫模型分析了橋面伸縮縫的最佳養護時機和全生命周期最小成本問題。Zayed等[8]在有關鋼橋的防護系統研究中，也利用馬爾可夫模型討論了鋼橋養護策略和全生命周期最小成本問題。戴宇文等[9]在有關橋梁管理系統的研究中，分別使用馬爾可夫過程和半馬爾可夫過程建立了橋梁退化模型，對橋梁的健康狀況進行了預測。盧新等[10]建立了基于改進的有限馬爾可夫鏈的橋梁性能退化預測系統，對橋梁的主要病害模式和主要病害因素進行了預測。張春霞等[11]基于馬爾可夫模型，對橋梁的養護時機進行了研究，給出了橋梁技術狀態和養護費用的預測模型。其中，最成功的應用實例是美國聯邦公路管理局基于馬爾可夫模型開發的PONTIS系統[12]。PONTIS系統于1991年完成第1版的開發，目前已被廣泛應用于美國的橋梁管理系統。上述研究對馬爾可夫模型在橋梁養護管理方面的應用作了一些有益的探索，并取得了良好的效果。同時，值得注意的是，在上述研究中還存在一些值得進一步改進和完善的地方。主要表現在以下兩個方面：

（1）馬爾可夫模型不能很好地應對監測數據的測量誤差問題。在馬爾可夫模型中，人們假定監測數據可以如實地反映系統的真實狀況。實際上，由于受監測方法、監測設備、監測位置以及數據的處理和解釋過程等因素的影響，管理者常常只能得到具有噪聲的數據，其中存在一定的測量誤差，包括系統誤差和隨機誤差[13-15]。正是因為這些測量誤差的存在，監測數據一般不能如實地反映橋梁的健康狀況。盡管人們可以借助一些校正方法在一定程度上減少誤差，但是無法做到完全消除誤差。為了更準確地進行橋梁健康狀況的等級評定，管理者必須正視監測數據中存在的誤差，探尋更加有效的等級評定方法。

（2）一階馬爾可夫過程不能充分地反映橋梁累積性病害的影響。在一階馬爾可夫模型中，給定系統的當前狀況和歷史狀況，假定系統未來狀況的演化趨勢僅依賴于當前狀況，而與歷史狀況無關。盡管這種假定在一定程度上是有效的，但同時也忽略了一些有用的統計特征，不能反映更多的歷史相關性[16]。一些應用研究表明，如果使用高階馬爾可夫過程來刻畫系統的演化過程，可以取得更好的效果[17-19]。同樣地，對于橋梁，高階馬爾可夫過程也可以更好地反映橋梁累積性病害的影響。假定橋梁健康狀況的性能指標有4類，分別記為“優、良、中、差”，下面考慮兩種情形：第1種情形，假設在t-1時刻和t時刻健康狀況分別為“優”和“中”；第2種情形，假設在t-1時刻和t時刻健康狀況分別為“良”和“中”。直觀上，人們不難理解在第1種情形下，健康狀態在t+1時刻演化為“中”的概率更大一些。即相對于一階馬爾可夫過程，高階馬爾可夫過程可以更充分地反映橋梁累積性病害的影響。

基于上述分析，本文提出了一種基于二階隱馬爾可夫模型的橋梁健康狀況分析與評定方法，其中同時考慮了測量誤差和累積性病害的影響。

1 二階隱馬爾可夫模型的構建

隱馬爾可夫模型（Hidden Markov Model，HMM）是一類具有雙重隨機過程的統計模型。其中，一個隨機過程為馬爾可夫過程，它描述了系統狀況的演化規律，是不可以直接觀測的；另一隨機過程描述了系統狀況與觀測值之間的統計關系，是可以直接觀測的[20]。隱馬爾可夫模型具有可靠的概率統計理論基礎和強有力的數學結構，目前已經被廣泛應用于語音識別、字符識別和計算生物學等領域[21-23]。在現有的隱馬爾可夫模型理論與應用研究中，主要是基于一階隱馬爾可夫模型。高階隱馬爾可夫模型作為一階隱馬爾可夫模型的一種改進，可以反映更多的歷史相關性，已吸引了一些研究者的關注，并在理論和應用研究上取得了一定的進展[16]。Mari等[24]利用二階隱馬爾可夫模型研究了時序數據的挖掘問題，結果表明，二階隱馬爾可夫模型對于平穩段定位具有非常好的性能。周順先等[25]研究了基于二階隱馬爾可夫模型的文本信息抽取算法，合理地考慮了概率和模型歷史狀態的關聯性，比基于一階隱馬爾可夫模型的算法具有更高的抽取精度。Ye等[26]給出了一種任意高階隱馬爾可夫模型解碼問題的新方法，為一階隱馬爾可夫模型和高階隱馬爾可夫模型的解碼問題提供了統一的算法框架。上述研究表明，相對于一階隱馬爾可夫模型，高階隱馬爾可夫模型能夠納入更多的統計特征，能夠對一些實際過程提供更加準確地描述。同時，這些研究也為高階隱馬爾可夫模型在實際中的應用提供了一定的理論基礎。

在橋梁的養護管理中，橋梁健康狀況的等級評定一般是依據橋梁定期的監測數據而進行的。由于系統誤差和隨機誤差的影響，管理者常常只能得到具有噪聲的監測數據，它們不能如實地反映橋梁的健康狀況，管理者需要通過分析這些帶有噪聲的監測數據挖掘橋梁健康的真實狀況。隱馬爾可夫模型為分析和處理這一類數據提供了一種可行的理論框架。

本文分別使用隨機過程｛st｝t≥1和｛ot｝t≥1表 示橋梁真實狀況的演化過程和監測過程，并假定橋梁健康狀況被分為N個等級，其中，“1”表示最好的狀況，“N”表示最差的狀況。假定管理者分別在t1、t2、t3時刻對橋梁狀況進行了監測，監測狀況分別記為：ot1=j1，ot2=j2，ot3=j3，對應的真實狀況分別記為st1=i1，st2=i2，st3=i3。其 中，i1，i2，i3，j1，j2，j3∈｛1，2，…，N｝。如果在監測時段內沒有對橋梁進行維護和修復處理，則橋梁的真實狀況應該是逐步退化的，即有i1≤i2≤i3。同時，由于測量誤差的影響，一般不滿足：i1=j1，i2=j2，i3=j3，即監測狀況往往不能如實地反映橋梁的真實狀況。例如，可能出現如圖1中所示的情況，即i1=j1，i2＞j2，i3＜j3。

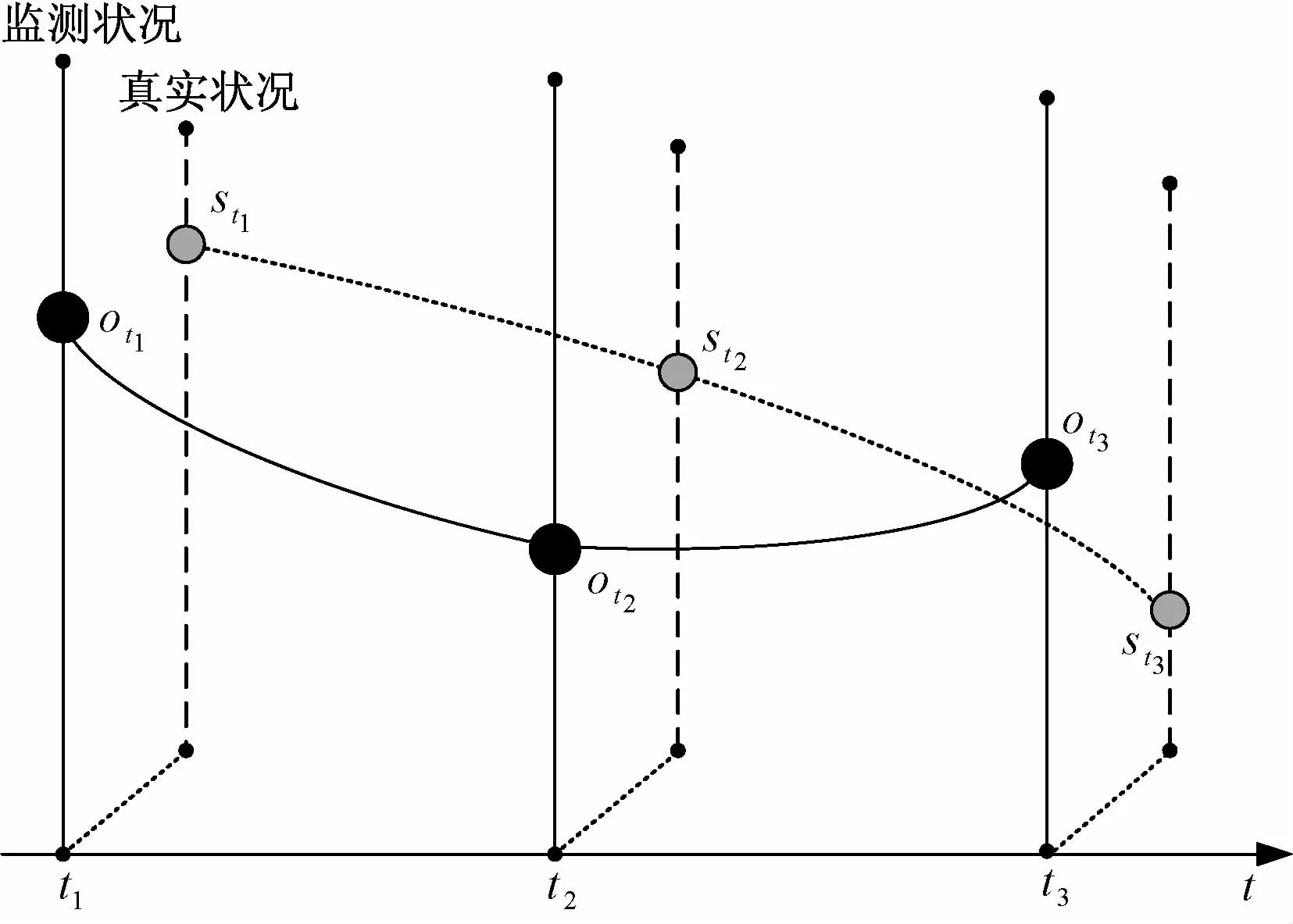
圖1 橋梁真實狀況與橋梁監測狀況誤差示意圖

另外，為了描述橋梁監測狀況與橋梁真實狀況之間的誤差和不確定性，本文使用一組離散概率分布bi（?）=P（ot=?|st=i）表示，其中i，?∈｛1，2，…，N｝。即當橋梁真實狀況為i時，監測狀況以概率bi（?）取得?。顯然，監測過程｛ot｝t≥1受到真實狀況演化過程｛st｝t≥1的控制。同時，本文假定橋梁監測狀況只受橋梁當前真實狀況的影響，而與橋梁的歷史狀況無關。

進一步，為了考慮累積性病害對橋梁的影響，使用二階馬爾可夫過程描述橋梁真實狀況的演化過程｛st｝t≥1，即滿足

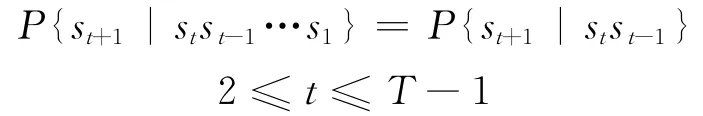
上述等式意味著，橋梁在t+1時刻的狀況不僅受到t時刻狀況的影響，而且還受到t-1時刻狀況的影響。二階馬爾可夫過程可以反映更多的歷史相關性，具體如圖2所示。

圖2 二階馬爾可夫過程示意圖

綜上所述，本文建立了一個二階隱馬爾可夫模型｛st，ot｝t≥1，其中包含了橋梁真實狀況的演化過程｛st｝t≥1和監測過程｛ot｝t≥1。具體如圖3所示。

圖3 二階隱馬爾可夫模型示意圖

下面具體說明二階隱馬爾可夫模型｛st，ot｝t≥1中所涉及的參數和符號：

T——監測次數，管理者以等時間間隔對橋梁進行了T次監測，即1≤t≤T。

S——橋梁健康狀況的指標集，用來描述橋梁的健康程度，不失一般性，可記S=｛1，2，…，N｝。其中，st∈S，“1”表示橋梁處于最好狀況，“N”表示橋梁處于最差狀況。

M——監測數據集，本文令M=S，ot∈M。

一步轉移概率aij——假定在對橋梁進行維護和修復后立即開始監測，則橋梁初始狀況應處在最好的情形，即s1=1。同時，假定橋梁后續狀況的演化不受維修前歷史狀況的影響，即s2只受到歷史狀況s1的影響。此時只需要考慮一步轉移概率，即

記A1=｛a1j｝。

兩步轉移概率aijk——假定橋梁在t-1時刻的真實狀況為i，在t時刻的真實狀況為j，記橋梁在t+1時刻真實狀況演化為k的概率為a ijk，即

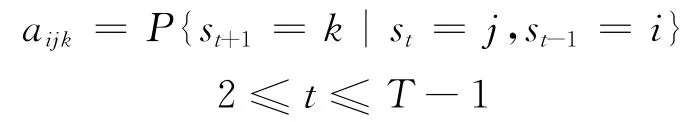
其中，i，j，k∈S。假設在監測時段內，管理者未對橋梁進行維護和修復處理。在這種情況下，橋梁的真實狀況應該是逐步退化的，即有

記A2=｛aijk｝。

bi（?）——符號發射概率，即

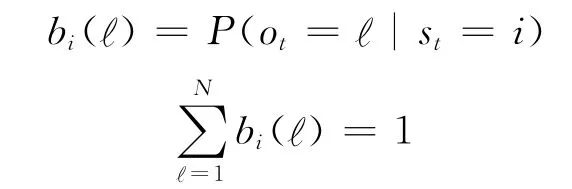
上述等式刻畫了測量誤差對監測數據的影響，當橋梁的真實狀況為i時，監測數據服從某個離散分布。并且，對于不同的狀況i，所對應的離散分布一般也是不同的。記B=｛bi（?）｝。

πi——初始狀況分布，即πi=P（s1=i）。記π=｛πi｝。假設在對橋梁進行監測前，管理者對橋梁進行了維護和修復處理，則

為了簡便起見，本文使用符號λ=（π，A1，A2，B）表示二階隱馬爾可夫模型的整體參數。這樣便得到一個具有參數為λ的二階隱馬爾可夫模型。其中，參數π、A1、A2刻畫了橋梁真實狀況的演化過程，參數B刻畫了橋梁狀況的監測過程。

假定管理者以等時間間隔對橋梁狀況進行監測，共進行了T次監測，獲得的監測數據序列記為O=o1o2…o T。由于系統誤差和隨機誤差的影響，監測數據一般不能如實反映橋梁的真實狀況，管理需要通過分析這些監測數據序列O=o1o2…o T來推斷橋梁的真實狀況。基于上述二階隱馬爾可夫模型，管理者可以通過解碼問題的Viterbi算法推斷出橋梁的真實狀況，從而為進一步制定橋梁養護措施提供科學的依據。下面具體說明二階隱馬爾可夫模型的解碼問題和相應的Viterbi算法，并說明其在橋梁健康狀況分析中的實際意義。

所謂二階隱馬爾可夫模型的解碼問題，一般是指在給定模型參數λ和監測數據序列O=o1o2…o T的前提下，確定一個狀況序列，使之滿足

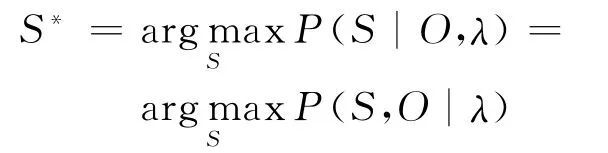
對于二階隱馬爾可夫模型的解碼問題，一般可使用基于動態規劃的Viterbi算法[27]來求解。為此，首先需要定義一個Viterbi變量：

其中，i1，i2∈S。它表示沿一條路徑s1s2…st-2st-1st，且st-1=i1，st=i2，產生監測數據序列o1o2…ot的最大概率。尋找最佳狀況序列的具體步驟：

（1）初始化

（2）遞歸計算

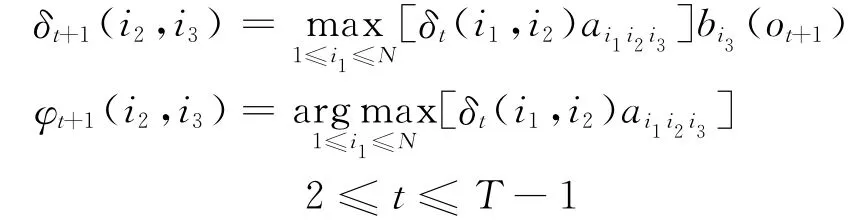
（3）中斷

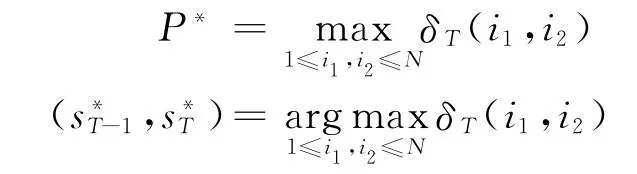
（4）路徑（最佳狀況序列）回溯

綜上所述，針對橋梁監測數據的測量誤差和累積性病害的影響，運用二階隱馬爾可夫模型和Viterbi算法，提出了一種橋梁健康狀況分析方法。基于橋梁狀況的監測數據序列O=o1o2…o T，管理者可以通過Viterbi算法分析橋梁健康狀況的真實演化過程，從而在一定程度上消除了測量誤差的影響，達到濾波的效果，對橋梁的真實狀況獲得更加準確的認知。

2 數值分析與計算實驗

根據我國公路橋梁技術狀況評定標準（JTG/T H21—2011），橋梁健康狀況一般被分為5個等級，本文分別使用“1、2、3、4、5”表示橋梁的健康程度。其中，“1”表示健康狀況處于最好情形，“5”表示健康狀況處于最差情形。據此，在下面的數值分析與計算實驗中，令N=5。在實際應用中，可以通過歷史監測數據和Baum-Welch算法[28]來獲得模型的具體參數λ。在下面的數值分析與計算實驗中，鑒于橋梁的實際演化規律，假定二階隱馬爾可夫模型的參數λ，具體如表1～4所示。

基于上述模型參數λ和二階隱馬爾可夫模型解碼問題的Viterbi算法，使用MATLAB軟件建立了一個m文件myviterbi（見附件）。為了說明本文所給方法的有效性和可靠性，對隨機給定的兩組監測數據進行了數值分析和計算實驗，具體如下：

表1 初始狀況概率

表2 一步狀態轉移概率

表3 兩步狀態轉移概率(3≤t≤T)

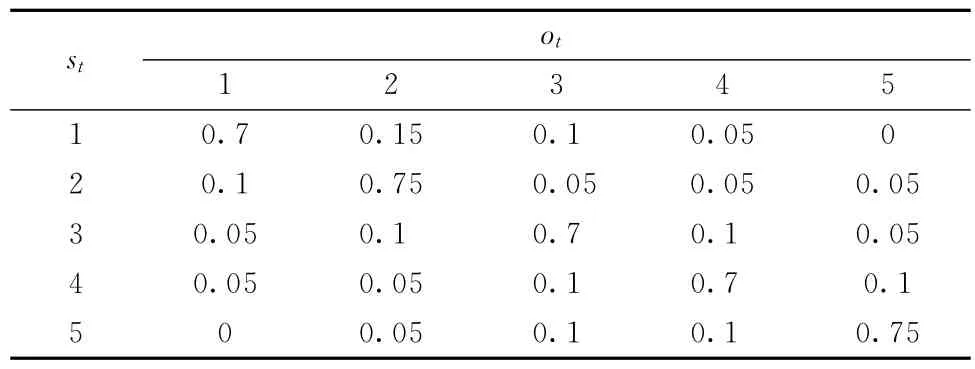
表4 符號發出概率(1≤t≤T)

實驗1隨機給定橋梁狀況的一組監測數據“131223353445552”，通過本文給出的分析方法，可以得出對應的橋梁真實狀況應為“111223333445555”。具體如表5和圖4所示。

實驗2隨機給定橋梁狀況的一組監測數據“311234333443544”，通過本文給出的分析方法，可以得出對應的橋梁真實狀況應為“111133333444444”。具體如表6和圖5所示。

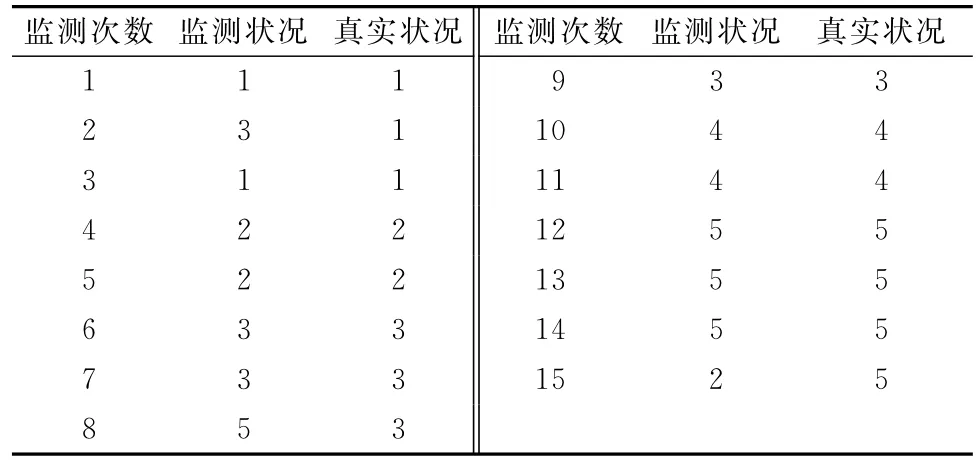
表5 橋梁實驗1數據

圖4 實驗1示意圖

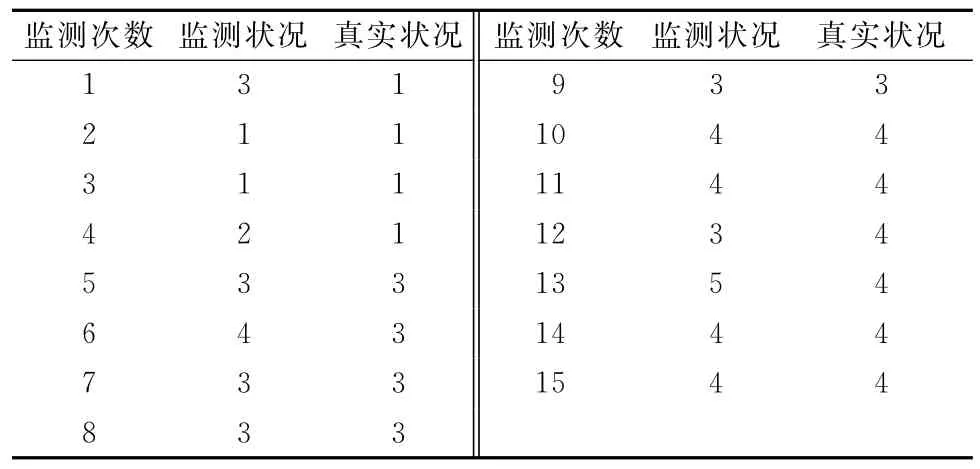
表6 橋梁實驗2數據

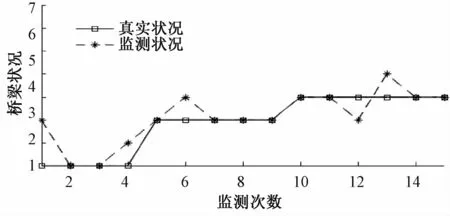
圖5 實驗2示意圖

實驗結果分析：

（1）在上述計算實驗中，隨機給定的兩組監測數據都存在測量誤差，不符合橋梁的實際演化規律。通過實驗分析得出的橋梁真實狀況序列都符合橋梁的實際演化規律，即在沒有對橋梁進行維護和修復的前提下，橋梁真實狀況總是逐步退化的。例如，在實驗1中，第2次監測數據“3”、第8次監測數據“5”、第15次監測數據“2”均為異常，肯定存在測量誤差。通過本文的分析方法，可以得出監測數據對應的橋梁真實狀況為“111223333445555”，該結果符合橋梁的實際演化規律，從而消除了測量誤差引起的異常數據。實驗分析結果可以使管理者更好地認識橋梁健康的真實狀況。

（2）在上述計算實驗中，假定橋梁的初始狀況是最好的。在實驗2中，隨機給定的第1次監測數據為“3”，這顯然也是一個存在測量誤差的數據。通過本文的分析方法，可以得出對應的橋梁真實狀況為“1”，該結果符合本文對橋梁初始狀況的假定，消除了測量誤差引起的異常數據。

（3）通過比較實驗1和實驗2，還發現一個有啟示的結果：如果在監測數據中出現一次“5”，此時橋梁的真實狀況不一定為最差情形，可能是測量誤差引起的；如果監測數據連續出現多次“5”，此時橋梁的真實狀況一定為最差情形。據此，管理者可以更好地把握橋梁健康的真實狀況，避免不必要的養護處理，降低橋梁全生命周期成本。

3 結語

本文使用二階馬爾可夫過程｛st｝t≥1刻畫了橋梁真實狀況的演化過程，從而更好地反映橋梁累積病害的影響。同時，使用隨機過程｛ot｝t≥1刻畫了橋梁真實狀況的監測過程，并通過一組離散概率分布｛bi（?）｝（1≤i≤N，1≤?≤N）描述了監測數據的測量誤差和不確定性。在此基礎上，建立一個二階隱馬爾可夫模型｛st，ot｝t≥1。其中，橋梁真實狀況的演化過程｛st｝t≥1是隱藏的，但橋梁真實狀況的監測過程｛ot｝t≥1可以被直接觀測。管理者需要通過分析具有噪聲的監測數據來了解橋梁的真實狀況。在二階隱馬爾可夫模型中，該問題被轉化為解碼問題，可以通過Viterbi算法來獲得橋梁的真實狀況。最后，通過數值分析與計算實驗說明了基于二階隱馬爾可夫模型的橋梁健康狀況分析方法的有效性和可靠性。

本文提出的基于二階隱馬爾可夫模型的橋梁健康狀況分析方法，同時考慮了測量誤差和橋梁累積病害的影響，可以更好地揭示橋梁的健康狀況，提高健康狀況等級評定的準確度。本文的研究對實際工程管理具有一定的借鑒價值：一方面，可以進一步豐富橋梁健康狀況評定技術，有助于管理者及時發現橋梁的病害和缺陷，避免引發安全事故，維系道路的安全與暢通，保障國家或地區社會經濟活動正常運行；另一方面，可以為橋梁養護管理提供更可靠的依據，提高橋梁養護的管理水平，以便對橋梁進行科學、有效、及時地養護與管理，降低橋梁的全生命周期成本，緩解公共財政的壓力。

另外，在本文的研究基礎上，有待于進一步展開的工作有：①將本文提出的方法應用到具體的橋梁健康狀況分析中，此時一般需要通過分析橋梁的歷史監測數據，并使用Baum-Welch算法獲得模型的具體參數；②本文使用二階馬爾可夫過程刻畫了橋梁真實狀況的演化過程，進一步，可將二階馬爾可夫模型推廣到任意高階的情形，這樣可以更好地反映橋梁演化的歷史相關性；③本文假定二階馬爾可夫過程是齊次的，即狀況轉移概率不會隨著時間而改變，進一步，可考慮用非齊次馬爾可夫過程來刻畫橋梁真實狀況的演化過程；④本文通過一組離散概率分布來刻畫監測數據的測量誤差，在具體的應用中，可通過分析歷史數據采用更合適的概率分布來描述；⑤本文給出的基于二階隱馬爾可夫模型的橋梁健康狀況分析方法可以應用于其他基礎設施，例如供水系統、道路系統和地鐵系統等。

附件