兩層供應鏈中數量競爭下零售商聯盟合作及穩定性研究

李昌文 ，周永務 ，郭金森，肖 旦

（1.華南理工大學 工商管理學院，廣州 510641；2.淮北師范大學 信息學院，安徽 淮北 235000）

競爭與合作已經成為當今世界發展的主題，并且，越來越多的學者從20世紀90年代中期已經注意到，競爭與合作是相互依存并同時影響公司和其他組織的運營策略[1-2]。競爭之中的合作包含很多方面，如供應鏈上下游之間的競合等。供應鏈上各個結點企業作為不同的利益主體，可以通過數量折扣、信息共享、利潤共享和回購等方式去獲取最大的利潤。而對于橫向上銷售同質產品的企業，可以通過聯合采購、共同提供售后服務以及庫存共享等方式進行合作。在現實生活中也有很多通過合作串謀定價（或串謀定量）的實例，Nagarajan等[3]指出，很多商品如煙草、酒、咖啡、山核桃、大米和小麥、金屬以及礦產都存在著這種聯盟情形。當這種聯盟存在于兩層的供應鏈結構時（即本文考慮的1個供應商，3個競爭的零售商），對于不同的供應商（供應商是領導者、零售商是領導者、供應商與零售商具有相同的市場力量），這種零售商聯盟在怎樣的情形下能夠保持穩定？

與本文相關的文獻有兩方面：①兩層分銷鏈中的競爭與合作；②聯盟形成的短視穩定性和遠視穩定性。在運營管理領域和經濟領域，目前已有大量文獻研究了橫向競爭性市場中的Nash均衡和Stackelberg均衡，以及供應鏈中的協調契約。關于價格與數量競爭下的合作模型，Nagarajan等[3]做了比較詳細的綜述。這些經濟文獻中關于競爭下的合作大部分考慮的是不同零售商之間的橫向合作，沒有考慮上游供應商參與的情況。Chen等[4]針對上游制造商在提供數量折扣的情形下，兩個下游競爭零售商進行合作訂貨后的利潤情況。上述文獻均未考慮兩層供應鏈中，下游存在競爭性零售商的情形下零售商聯盟穩定性的問題。而關于聯盟穩定性的討論主要分為短視穩定性和遠視穩定性兩方面。早期關于聯盟穩定性的研究大多都是假設參與者是短視的，即描述穩定性概念是靜態穩定的，如Nash穩定和強Nash穩定等[5-6]，靜態穩定僅考慮參與者的一步“叛逃”能否獲得更高的利潤。但是，在參與人發生一步“叛逃”之后有可能會引起其他參與人的進一步的一系列“叛逃”，為了刻畫這種多步叛逃下的結果，Chwe[7]提出了遠視參與者的動態穩定性概念。Granot等[8]引入最大一致集（LCS）等合作博弈的解概念運用到供應鏈中，討論了遠視零售商聯盟結構的穩定性。Nagarajan等[9]、Granot等[10]對組裝供應鏈系統中遠視供應商聯盟的穩定性進行了一系列的探討。Nagarajan等[11]在3種不同的上下游博弈框架下，討論了裝配供應鏈系統中供應商聯盟的穩定性。Sosic[12]研究了3層供應鏈中信息共享聯盟的遠視穩定性。Nagarajan等[13]討論了團購聯盟的穩定性問題。鄭士源等[14]利用遠視穩定概念找到了穩定的航空聯盟，并基于運輸合作模型分析了運輸聯盟的動態穩定性[15]。周永務等[16]考慮了上下游存在3種博弈情形下的零售商間具有價格競爭的聯盟穩定性。

不同于文獻[16]，本文考慮的是3個零售商數量競爭下不同合作聯盟的穩定性問題。數量競爭的聯盟有很多，Alhajji等[17]指出，一些商品如鉆石、咖啡、石油等都存在著這種聯盟合作。針對上述存在的實際問題中的零售商聯盟合作以及供應商與零售商可能存在的3種博弈結構[11，16]，本文研究了1個上游供應商和3個在數量上相互競爭的下游零售商組成的分銷供應鏈系統，在3種不同的博弈框架下（供應商是領導者、零售商是領導者、供應商與零售商具有相同的市場力量）研究不同的競爭強度對聯盟穩定性的影響。結果表明：在Stackelberg模型中，無論誰是領導者，大聯盟都不是短視穩定的，然而卻是遠視穩定的；而在垂直Nash模型中，只有當競爭強度相對較小時，大聯盟是短視穩定的，任何情形下，大聯盟都是遠視穩定的。對于不同的競爭強度，本文還給出了遠視情形下可能存在的其他的穩定聯盟結構。

1 分銷供應鏈模型

記供應商為0，下游3個數量上相互競爭的零售商記為N=｛1，2，3｝，零售商i∈N的定價p i和自身產品數量qi與其他零售商產品數量q j有關，本文使用下述逆需求函數：

式中：α＞0，β＞0刻畫了零售商i自身的需求對價格的影響；γ＞0反映了零售商間的競爭強度，并且滿足β＞γ，因為相比較于其他零售商，零售商價格受自身的需求更加敏感。上述逆需求函數在經濟學和市場營銷學的文獻中較為普遍[18-19]。

本文假設零售商能自由結盟，并且假設同一聯盟內的零售商向供應商訂購相同數量的產品。記零售商（也稱為參與人）之間自由形成合作聯盟Z?N，N=｛1，2，3｝。一種聯盟結構是指對集合N的一種分割L=｛Z1，Z2，…，Zm｝，其中，

特別地，所有零售商結盟形成的聯盟結構｛N｝稱為大聯盟。對于任意給定的一個聯盟結構L，聯盟Zk∈L中任意一個零售商的逆需求函數均可寫為

為了表示方便，令γ=βb，0＜b＜1。供應商產品的單位成本為c，零售商的銷售成本為0，每個零售商的訂貨量等于其在市場上的需求量。根據市場上存在的供應商與零售商地位的不同[11]，考慮上下游之間3種不同的競爭模型：①供應商Stackelberg模型。在此模型中，供應商是Stackelberg博弈的領導者，首先決策給予零售商的批發價格，然后下游零售商（聯盟）同時決策各自最優的訂貨量。這種博弈下，供應商在市場上相對于零售商而言具有強大的力量，如供應商如果掌握一些比較稀缺的商品時，在觀察到市場上零售商的反應后，優先決策自己的最優批發價格。②供應商-零售商垂直Nash模型。在此模型中，供應商和下游的零售商（聯盟）同時決策最優批發價格和最優訂貨量。在這里，供應商和零售商（聯盟）在市場上具有對等的影響力。③零售商Stackelberg模型。其中零售商（聯盟）相對于供應商而言，在市場上具有更大的影響力。在觀察到供應商的反應函數后，零售商（聯盟）優先決策最優的訂貨量，然后供應商決策最優的批發價格。這種情形在市場上很多，例如家樂福、沃爾瑪等大型零售商相對于一些小型的供應商具有決策的優先權。

1.1 供應商Stacke1berg模型(S)

首先考慮供應商作為Stackelberg領導者的情形，供應商首先決策產品的批發價格，然后零售商（聯盟）決策最優的訂貨量，下面分3種不同的聯盟結構進行討論。

1.1.1 互不結盟 當3個零售商不結盟時，此時聯盟結構為，=｛｛1｝，｛2｝，｛3｝｝，首先，供應商決策最優批發價格，各個零售商決策各自的訂貨量，此時模型為：

為第i個零售商的市場價格。求解此優化問題，可得博弈的均衡解：

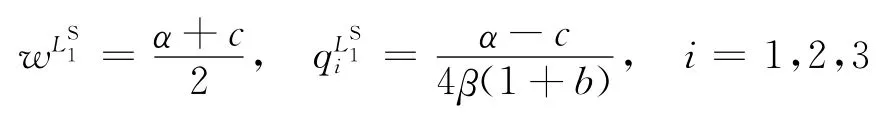
供應商和零售商的利潤分別為：

整個供應鏈系統總的利潤為

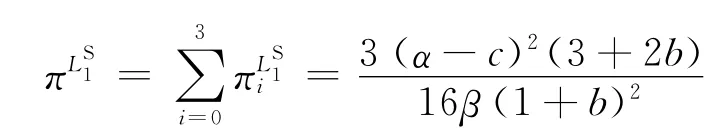
1.1.2 兩個零售商結盟 當任意兩個零售商結盟時，零售商的聯盟結構為，=｛｛1，2｝，｛3｝｝，｛｛1，3｝，｛2｝｝，或｛｛2，3｝，｛1｝｝。供應商首先決策批發價格，聯盟內零售商和聯盟外零售商同時決策最優訂貨量和，此時模型為：

其中：為供應商的利潤和分別為聯盟中和聯盟外零售商的利潤；

分別為聯盟內和聯盟外零售商的價格。求解此優化問題，可得博弈的均衡解：

供應商、聯盟內零售商和聯盟外零售商的利潤分別為：

此時，整個供應鏈系統總利潤為

1.1.3 3個零售商結盟 當3個零售商形成大聯盟=｛N｝時，供應商首先決策最優批發價格，聯盟中零售商決策最優訂貨量，此時模型為：

其中：和分別為供應商和第i個零售商的利潤；

為大聯盟內零售商的價格。求解此優化問題，可得均衡解：

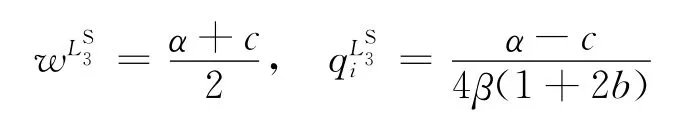
供應商和零售商的利潤分別為：

此時，整個供應鏈系統總利潤為

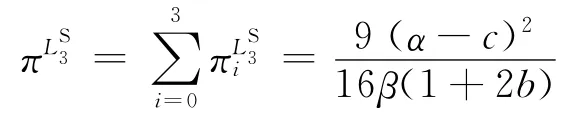
具體的求解過程見附錄。

性質1不同的聯盟結構下，有如下關系成立：

本文發現，在供應商作為Stackelberg領導者情形下，任意聯盟結構下供應商給予零售商的批發價格都是相同的，但是下游所有零售商的訂貨量在大聯盟時最少，從而供應商在所有零售商結盟時獲得的利潤最少。對于供應商而言，當下游所有零售商均不結盟時獲利最多，即當供應商在市場上具有較強的統治力時，保持市場上一定數量的零售商和適當的競爭，對供應商而言是有好處的。從整個供應鏈系統的角度，當下游零售商結盟時，系統的利潤也會減小，即下游零售商結盟傷害了整個供應鏈系統的利潤。從零售商的角度，是否結盟受到競爭強度的影響。當其中某兩個零售商結盟時，處于聯盟外零售商的利潤最高。特別需要強調的是，當兩個零售商結盟時，聯盟內零售商的利潤在0.555＜b＜1時，比不聯盟情形下的利潤更低，故對于零售商而言，是否結盟視競爭強度的不同需要作出不同的決策。

1.2 垂直Nash模型(V)

這里考慮所有參與人同時決策的情形，即供應商和零售商聯盟同時決策產品的批發價格和產量。下面分3種情況進行討論。

1.2.1 互不結盟 當零售商之間不形成任何聯盟時，記此時的聯盟結構為，=｛｛1｝，｛2｝，｛3｝｝，供應商和3個零售商同時決策最優的批發價格和最優訂貨量，此時模型為：

其中：為供應商的利潤為第i個零售商的利潤；

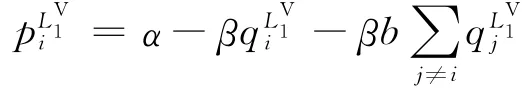
為第i個零售商的市場價格。求解此優化問題，可得博弈的均衡解：

供應商和零售商的利潤分別為：

整個供應鏈系統的利潤為

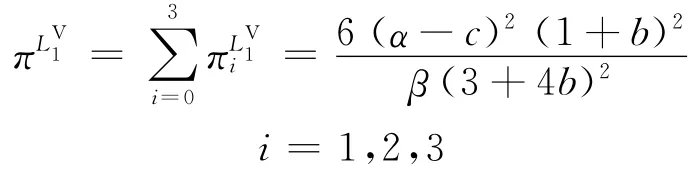
1.2.2 兩個零售商結盟 當任意兩個零售商結盟時，此時的零售商聯盟結構為，=｛｛1，2｝，｛3｝｝，｛｛1，3｝，｛2｝｝，或｛｛2，3｝，｛1｝｝。供應商0、聯盟內零售商和聯盟外零售商同時決策批發價格，訂貨量和，此時模型為：

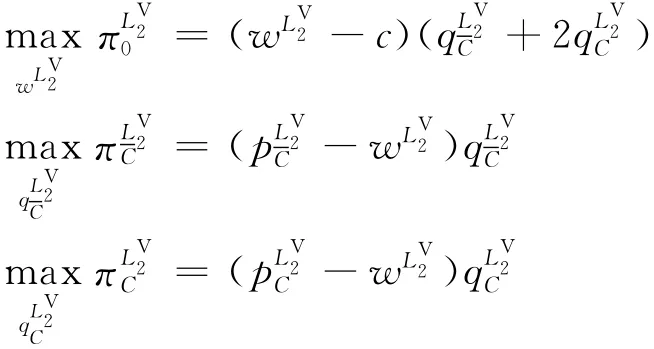
其中：為供應商的利潤和分別為聯盟中和聯盟外零售商的利潤；

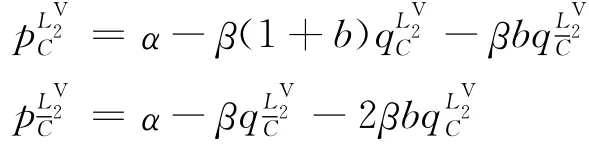
分別為聯盟內和聯盟外零售商的價格。求解此優化問題，可得博弈的均衡解：

供應商、聯盟內零售商和聯盟外的零售商的利潤分別為：

此時，整個供應鏈系統總利潤為

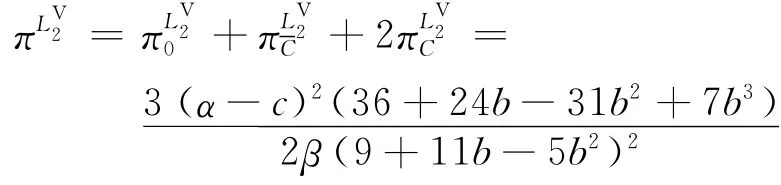
1.2.3 3 個零售商結盟 當3個零售商形成大聯盟=｛N｝時，供應商和聯盟同時決策最優批發價格和訂貨量，此時模型為：

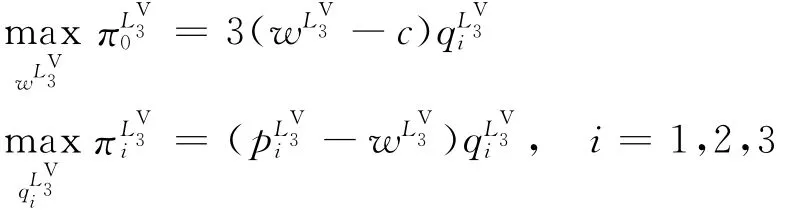
其中：和分別為供應商和第i個零售商的利潤；

為大聯盟內零售商的價格。求解此優化問題，可得均衡解：

供應商和零售商的利潤分別為：

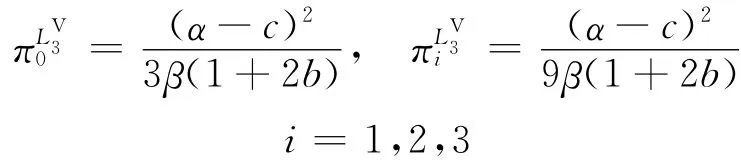
此時，整個供應鏈系統總利潤為

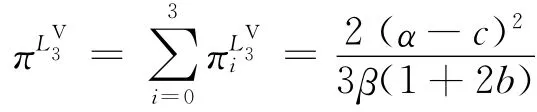
性質2不同的聯盟結構下，有如下關系成立：

（1）批發價格（j=1，2，3）滿 足＜

（5）供應鏈系統的利潤（j=1，2，3）隨著競爭強度b的增大而減小，并且有

在供應商和零售商（聯盟）縱向Nash博弈下，供應商給予零售商（聯盟）的批發價格隨著零售商聯盟內零售商數量的增大而減小，即下游零售商的結盟使得上游供應商的批發價格降低，同時也影響了下游的訂貨量。對于供應商而言，其利潤在大聯盟情況下是最低的；對于整個供應鏈系統而言，大聯盟情況下的利潤也是最低的。從供應商的角度，保持一定的下游零售商的數量是有好處的，供應商并不希望下游出現結盟的情況。從零售商的角度，是否結盟仍然是與競爭強度有關。可見，當兩個零售商結盟時，聯盟內零售商的利潤是各種情況下最少的，聯盟外零售商的利潤總是比聯盟內的利潤要高，故在垂直Nash模型中，兩個零售商結盟總是不可取的。

1.3 零售商Stacke1berg模型(R)

這里考慮零售商（聯盟）作為博弈領導者的情形，即零售商（聯盟）首先決策最優的訂貨量，然后供應商決策最優的批發價格。下面分3種情況討論。

1.3.1 互不結盟 當零售商之間不形成任何聯盟時，記此時零售商聯盟結構為，，｛3｝｝。3個零售商首先決策最優訂貨量，然后供應商決策最優批發價格，此時模型為：

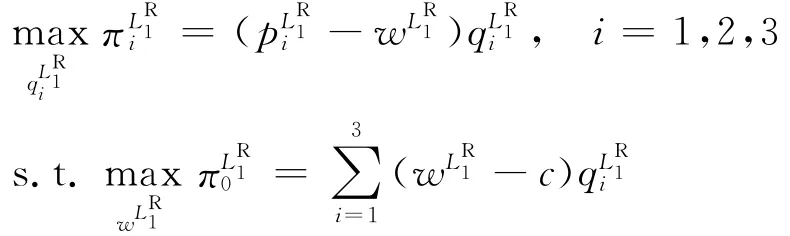
為第i個零售商的市場價格。求解此優化問題，可得博弈的均衡解：

供應商和零售商的利潤分別為：

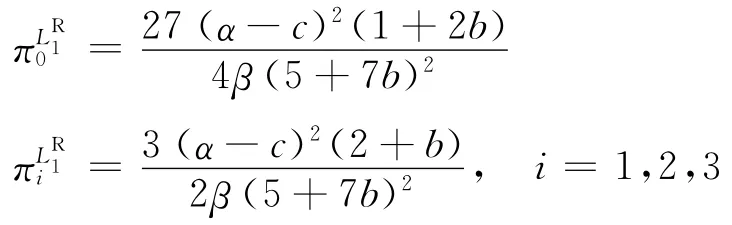
此時，整個供應鏈系統的利潤為

1.3.2 兩個零售商結盟 當任意兩個零售商結盟時，則兩個零售商聯盟結構為，=｛｛1，2｝，｛3｝｝，｛｛1，3｝，｛2｝｝，或｛｛2，3｝，｛1｝｝，聯盟內零售商和聯盟外零售商同時決策最優訂貨量和，供應商最后決策最優批發價格，此時模型為：

其中：為供應商的利潤和分別為聯盟中和聯盟外零售商的利潤；

分別為聯盟內和聯盟外零售商的價格。求解此優化問題，可得博弈的均衡解：

供應商、聯盟內零售商和聯盟外零售商的利潤分別為：

此時，整個供應鏈系統的利潤為

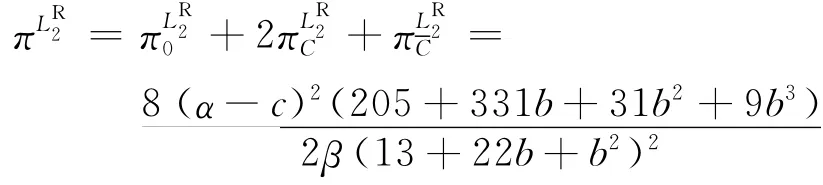
1.3.3 3個零售商結盟 當3個零售商形成大聯盟=N時，聯盟內零售商首先決策最優訂貨量，然后供應商決策最優批發價格，此時模型為：

其中：和分別為供應商和第i個零售商的利潤；

為大聯盟內零售商的價格。求解此優化問題，可得均衡解：

供應商和零售商的利潤分別為：

此時，整個供應鏈系統的利潤為

性質3不同的聯盟結構下，有如下關系成立：

在零售商（聯盟）作為Stackelberg博弈領導者情形下，供應商給予零售商（聯盟）的批發價格隨著聯盟內零售商數量的增大而減小，即下游零售商結盟使得上游供應商的批發價格減小；同時，結盟也影響了下游零售商的訂貨量，特別是在大聯盟下訂貨量是最小的，而這些影響又使得供應商的利潤隨著下游零售商的結盟而變小。這與前面兩種情況類似。對于零售商而言，此種情形和供應商Stackelberg類似，只是競爭強度的閾值不同。

2 零售商聯盟的穩定結構

由上述不同的競爭模型可見，零售商是否結盟與競爭強度有很大的關系；另一方面，對于零售商結盟后的聯盟結構是否能夠維持穩定，也是需要考慮的一個方向。例如在供應商Stackelberg模型中，大聯盟N中零售商3的利潤比聯盟｛｛12｝，3｝中零售商3的利潤要小，此時對于零售商3而言，從大聯盟N中獨立出來，獲利會更多，所以，此種情形下大聯盟并不穩定。在合作博弈中有短視穩定性和遠視穩定性之分。合作博弈中的Nash穩定和強Nash穩定均屬于短視穩定，其判定的方法是看其參與人（聯盟）從某個聯盟結構中發生一步“叛逃”之后，是否使得其利潤增加。而對于遠視穩定性，是從參與人發生多步“叛逃”的結果來判斷其是否穩定。因為某個參與人的一步“叛逃”，使得叛逃的參與人的利潤增加后，致使其他參與人發生一系列叛逃行為，這也就是從聯盟動態或長遠的角度來看待聯盟的穩定性問題。針對這種遠視穩定性的概念，Chwe[20]提出了遠視參與者的概念，并且，采用最大一致集（LCS）來刻畫遠視參與者聯盟的穩定結構，具體相關定義見文獻[3，17]。

2.1 短視零售商聯盟的穩定性

下面給出3種競爭模型中零售商聯盟的短視穩定性，即從合作博弈中Nash穩定和強Nash穩定的角度考慮零售商（聯盟）的穩定性。

定理1在供應商Stackelberg模型中：①當0＜b＜0.555時，兩個零售商聯盟結構為=｛｛1，2｝，｛3｝｝，｛｛1，3｝，｛2｝｝，｛｛2，3｝，｛1｝｝是Nash穩定的；②當0.555＜b＜1時，所有的聯盟結構都不是Nash穩定的。

證明見附錄。

定理1說明，當競爭強度較小（0＜b＜0.555）時，兩個零售商的聯盟是短視穩定的，即其中任意一個零售商都不會發生叛逃行為；但是當競爭強度較大（0.555＜b＜1）時，任意一個聯盟結構都是不穩定的，其中的參與人都會發生一步的叛逃行為，使得原有的聯盟結構不穩定。但是從遠視的角度，是否會有不同的結果，下面給出具體答案。

定理2在垂直Nash模型中：①當0＜b＜0.832時，大聯盟是Nash穩定的；②當0.832＜b＜1時，所有的聯盟結構都不是Nash穩定的。

定理3在零售商Stackelberg模型中：①當0＜b＜0.314時，兩個零售商聯盟結構為=｛｛1，2｝，｛3｝｝，｛｛1，3｝，｛2｝｝，｛｛2，3｝，｛1｝｝是Nash穩定的；②當0.314＜b＜1時，所有的聯盟結構都不是Nash穩定的。

2.2 遠視零售商聯盟的穩定性

首先，給出不同競爭強度下的零售商的聯盟偏好關系：

性質4

（1）供應商Stackelberg模型中，當0＜b＜0.555時，零售商的聯盟偏好關系為當0.555＜b＜1時，零售商的聯盟偏好關系為

（2）垂直Nash模型中，當0＜b≤0.832時，零售商的聯盟偏好關系為；當0.832＜b＜1時，零售商的聯盟偏好關系為

（3）零售商Stackelberg模型中，當0＜b≤0.314時，零售商的聯盟偏好關系為當0.314＜b＜1時，零售商的聯盟偏好關系為

根據上述不同模型中的聯盟偏好關系，結合最大一致集（LCS）的定義，有如下遠視零售商聯盟的結論。

定理4在供應商Stackelberg模型中：①當0＜b＜0.555時∈LCS；②當0.555＜b＜1時∈LCS。

證明見附錄。

由定理4可得結論：無論競爭強度是多少，大聯盟都是遠視穩定的，這與定理1中當0＜b＜0.555時，大聯盟從短視的角度不是Nash穩定形成了對比。原因在于，從遠視的角度考慮聯盟穩定性時，不但考慮某個參與人一步叛逃的結果，而且還需考慮這一步叛逃后所引起的其他參與人的一系列叛逃行為。即當0＜b＜0.555時，對于大聯盟N而言，零售商3發現，一步叛逃后形成聯盟結構｛｛1，2｝，3｝對自己是有利的，這從短視的角度即N是不穩定的。但是，這一步叛逃會引起聯盟內參與人1或2的繼續叛逃，因為這對他們是有利的，從而進一步的叛逃后聯盟結構變為｛｛1｝，｛2｝，｛3｝｝。最終所有的零售商發現，大家一起合作時的聯盟結構N對所有參與人而言，比｛｛1，2｝，3｝和｛｛1｝，｛2｝，｛3｝｝都要有利，即大聯盟N仍然是一系列叛逃后的結果。從長遠來看，所有參與人在大聯盟N內不會發生叛逃。而對于聯盟結構而言，當0＜b＜0.555時，無論從短視的角度還是遠視的角度，都是穩定的；而當0.555＜b＜1時，無論從短視角度還是遠視角度都是不穩定的。這也就說明，在3個零售商數量競爭下，所有零售商結盟總是有利的。而在競爭強度不太大（0＜b＜0.555）時，任意兩個零售商結盟時也很有可能發生，并且能夠長期穩定；但是當競爭強度較大（0.555＜b＜1）時，能夠長期穩定的聯盟是大聯盟N。

定理5在垂直Nash模型中，∈LCS。

定理6在零售商Stackelberg模型中：①當0＜b＜0.314時，∈LCS；②當0.314＜b＜1時∈LCS。

由上述3個定理可見，在市場中無論哪一方具有統治力，數量競爭下的零售商所形成的大聯盟從遠視的角度都是穩定的聯盟結構，這與短視中的Nash穩定性有很大的不同。從短視的角度，大聯盟只是在滿足一定的競爭強度時才是穩定的。即當市場上的零售商處于對稱地位時，大家彼此合作構成大聯盟時對彼此之間是有利的。這也符合當今世界中競爭與合作并存的局面。另外，還發現，除了大聯盟外，在供應商Stackelberg模型和零售商Stackelberg模型中，兩人的聯盟結構也是從遠視角度穩定的，只是存在區間的競爭強度不同。在供應商和零售商市場力量相當時，即垂直Nash模型中，只有大聯盟是遠視穩定的。

3 結語

在零售商數量競爭下，本文利用合作博弈論中穩定性的概念，從零售商結盟合作訂貨的角度描述了聯盟的短視穩定性和遠視穩定性。從零售商的角度，無論在供應商Stackelberg模型、垂直Nash模型和零售商Stackelberg模型中，短視的零售商在競爭強度相對較小時，都會選擇大聯盟；但是當競爭強度相對較大時，短視的零售商在大聯盟中都會發生叛逃行為，即短視的零售商大聯盟是不穩定的。但是從遠視的角度，無論哪一種模型下，大聯盟都是遠視穩定的。

本文的結論對于3個競爭零售商結盟具有一些有意義的管理啟示。對于一個大聯盟中的零售商而言，有可能會因為叛逃而獲得更高的利潤。但是當零售商具有“遠見”時，會發現不論是哪種博弈框架下，無論競爭強度是多少，這種叛逃很可能帶來聯盟的不穩定，并且降低了自身的利潤。在這種情形下，零售商不會“短視”的“叛逃”出聯盟，而寧愿留在大聯盟中。另一個方面，當競爭強度較小時，對于兩種Stackelberg模型，有“遠見”的零售商也會留在兩人聯盟中。現實生活中存在著數量競爭下的聯盟合作，本文的研究結果也表明，對于“遠視”零售商而言，這些結盟總是有好處的。這與一般采用靜態穩定性討論聯盟合作穩定性有很大不同，也為現實生活中的結盟活動提供了理論基礎。

當零售商是遠視參與人時，無論在供應商Stackelberg模型、垂直Nash模型和零售商Stackelberg模型中，隨著零售商的結盟，供應商的利潤都是降低的，故進一步應該考慮供應商設計某種契約使得隨著零售商的結盟，供應商的利潤也會相應的有所增加。另外，在零售商結盟時，考慮聯盟運作時的運作費用也是值得研究的方向。當然，本文只是針對對稱性的零售商和確定情形進行了討論，進一步值得考慮的方向是不對稱以及隨機情形下的零售商結盟的穩定性問題。

附錄

供應商Stackelberg模型（S）中訂貨量和批發價的求解：

采用逆向歸納法進行求解。

（1）互不結盟時，對零售商i的利潤函數關于求導并令其等于0，有b）]，從而，兩邊關于求導并令其等于0，有從而

兩邊關于求導，并令其等于0，有=（α+c）/2，從而

垂直Nash模型（V）中訂貨量和批發價格的求解：

記零售商i的邊際收益為m i，即

（1）互不結盟時，對零售商i的利潤函數關于求導并令其等于0，同時對供應商的利潤函數關于求導令其等于0，有：

求解上述方程組后，有：

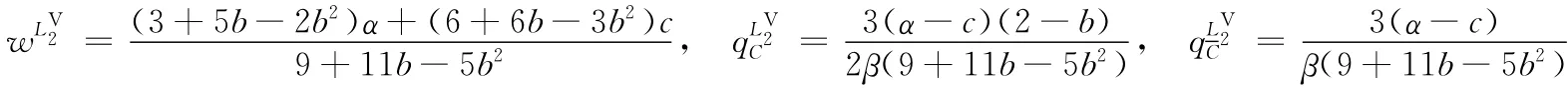
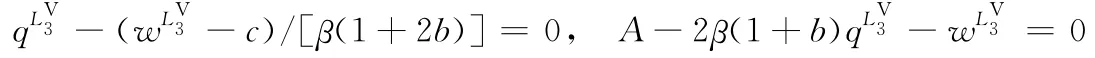
零售商Stackelberg模型（R）中訂貨量和批發價的求解：

求解方法類似于前面兩種模型，這里從略。

定理1的證明：

證明

（1）首先，證明當0≤b＜0.555時和都不是Nash穩定的。由性質1（3）可知，當聯盟結構為=｛1，2，3｝時，由于，故對｝內任意兩個零售商而言，結盟以后利潤都會變大，即任意兩個零售商都有結盟的動機，聯盟結構此時變為。因此，聯盟結構不是Nash穩定的。當聯盟結構為=N時，由于，故對大聯盟內的某個零售商經過一步叛逃后，聯盟=N變為時對聯盟外的零售商更有利。因此，聯盟結構不是Nash穩定的。

當零售商聯盟結構為=｛｛1，2｝，｛3｝｝，｛｛1，3｝，｛2｝｝，｛｛2，3｝，｛1｝｝時，不論是聯盟內零售商或聯盟外零售商，一步“叛逃”后都不能使得利潤增加。因此，零售商聯盟結構是Nash穩定的。

（2）當0＜b＜0.555時，由性質1中，首先，有=｛1，2，3｝不是Nash穩定的，由可知，3個零售商有結盟的動機；其次=｛｛1，2｝，｛3｝｝，｛｛1，3｝，｛2｝｝，｛｛2，3｝，｛1｝｝不是Nash穩定的，由容易看出，聯盟內零售商有“叛逃“的動機；最后都不是Nash穩定的，這與（1）類似。

定理4的證明：

證明

（1）當0＜b＜0.555時，由性質4可知，零售商i的聯盟偏好關系為，首先，考慮當前的聯盟結構為L=，不妨假設=｛｛1，2｝，3｝，則參與人一步“叛逃”之后的聯盟結構為

①如果V=，則S=｛1｝或S=｛2｝。考慮叛逃過程：｛（1，2，3｝→1，2｛｛1，2｝，3｝，由于｛（1，2，3｝?1，2｛｛1，2｝，3｝，如果記B=｛｛1，2｝，3｝，則有V?B，但是L□SB；

②如果V=，則S=｛1，2，3｝，令B=，則有V=B，但是L□SB。

綜上所述，根據最大一致集（LCS）的定義，有∈LCS。

下面考慮聯盟結構為大聯盟L==N，則任意1個或2個參與人一步“叛逃”后的聯盟結構為V=。不妨假設=｛｛1，2｝，3｝，則S=｛1，2｝，或S=｛3｝。考慮叛逃過程：｛｛1，2｝，3｝→1｛1，2，3｝→1，2，3N，由于｛｛1，2｝，3｝?1｛N｝且｛1，2，3｝?1，2，3｛N｝，如果記B=N，則有V=｛｛1，2｝，3｝?N=B，但是，顯然，L□SB。根據最大一致集（LCS）的定義，有｛（012）｝∈LCS。

最后，若聯盟結構為L=，則一步“叛逃”之后的聯盟結構為V=或，可以發現，不能找到聯盟結構B，使得V=B或V?B，使得L□SB。因此?LCS。

（2）當0.555＜b＜1時，由性質1可知，零售商i的聯盟偏好關系為和的證明與（1）類似。下面證明當0.555＜b＜1時?LCS。

當聯盟結構為L=，不妨假設=｛｛1，2｝，3｝，則參與人一步“叛逃”后的聯盟結構為

①如果V=，則S=｛1｝，或S=｛2｝，令B=，則有V=B，并且L?SB；

②如果V=，則S=｛1，2，3｝，令B=，則有V=B，并且L?1，2B。

綜上所述，根據最大一致集（LCS）的定義，有?LCS。