基于支持向量機的節假日進出站客流預測方法
謝 俏 葉紅霞
(廣州地鐵集團有限公司, 510330, 廣州//第一作者, 工程師)
隨著城市軌道交通網絡格局的逐步形成,網絡客流規模持續攀升,運營壓力日益凸顯。運營管理部門需要提前掌握節假日期間客流量的變化趨勢,以制定和實施合適的運營管理及客流組織計劃[1]。因此,需要利用數據挖掘技術,深入剖析節假日客流特征規律,精準地預測節假日期間網絡客流分布狀態和趨勢。
常用的進出站客流量預測方法分為線性預測方法和非線性預測方法。線性預測方法包括時間序列模型[2-3]、卡爾曼濾波模型[4-5]等,由于它們的理論基礎是線性估計模型,當客流呈現非線性、隨機性等特征時,模型的預測性能逐漸變差。
非線性預測方法包括非參數回歸[6-8]、神經網絡模型[9-12]、支持向量機[13-14]等,非線性預測方法理論上更加符合客流非線性、不平穩等復雜特征的場景。非參數回歸主要依賴歷史數據描述因變量和自變量之間的關系,尋找歷史數據與當前點相似的“近鄰”,把當前的狀態描述為一個過去某種狀態的“近鄰狀態”,并用這些近鄰預測下一時刻值,模型對歷史數據的要求較高,且需要大量歷史數據以從中提取有用信息。神經網絡模型存在局部最優、過擬合等弊端,且對樣本量要求高,樣本較少時,預測性能會大大降低。支持向量機與神經網絡相比,其突出優點是依據結構風險最小化原則進行學習,可以在預測精度和推廣能力之間尋找折中點,再加上核函數的巧妙利用,較好地解決了小樣本、非線性、維數災難、過學習及局部最優等問題。
節假日期間地鐵的進出站客流是一種不穩定的并隱含著大量動態特征的非線性、非平穩時間序列,客流規律較為復雜,不易捕捉其特征,且存在數據量樣本較少的情況。考慮上述節假日客流特征,本文選取支持向量機模型對節假日期間進出站客流進行預測。
1 節假日期間進出站客流特征分析
為對進出站客流進行較好的預測,需要充分挖掘進出站客流的規律,下文以廣州地鐵2014—2017年國慶假期期間各站點的進出站客流量的歷史數據進行特征分析。
考慮2014—2016年國慶假期的放假安排相同,假期均為10月1—7日共7天時間,而2017年國慶假期為10月1—8日共8天時間(10月4日為中秋節),為了合理統計國慶假期的客流規律,對2017年的國慶假期進行壓縮,將國慶假期的第四天和第五天客流量的平均值作為第四天的,第六天、第七天、第八天的客流量分別作為第五天、第六天和第七天的,通過該方法建立了2014—2017年國慶假期客流數據的歷史數據庫。
通過分析2014—2017年國慶假期各車站的進出站客流量數據可知,節日期間各站每天的進出站客流量與節日期間的平均進出站客流量的比例是基本穩定的。以西村站為例,如圖1所示,西村站2014—2017年國慶假期中平均進出站客流量與每天進出站量的比例較為穩定。

a) 進站客流量比例
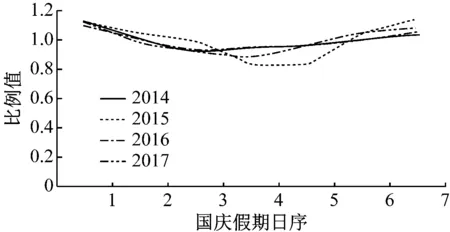
b) 出站客流量比例
圖1 西村站國慶假期每日進出站客流量與節日期間平均進出站客流量的比例
此外,按車站分類建模有利于將規律相近的車站放在一起,便于機器學習規律,從而提高預測精度。節假日期間的出行者以休閑娛樂、購物、旅游等為出行目的居多,因此商業區、景點區等附近的地鐵站的進出站客流量驟增,而辦公區等附近的地鐵站的進出站客流量則減少。同時市區車站、郊區車站的進出站客流量也呈現出不同的特征。基于此,在預測過程中將地鐵車站分為商業或景點類、市區站其他類、郊區站其他類。
2 節假日進出站客流預測模型
2.1 模型框架
根據上一節對國慶假期期間車站進出站客流變化規律特征的研究,發現節假日期間每天進出站客流量與平均進出站客流量的比例較為穩定。因此,對于節假日期間的客流預測,本文構建節假日期間平均進出站客流量預測模型。考慮到節假日期間乘客出行較為自由,無論是出行時間分布,還是出行目的都表現出與平常日不同的特征,因此,建立節假日期間平均進出站客流量預測模型時,不僅要考慮歷史節假日期間客流量均值與歷史平常日進出站客流量之間的關系,而且要考慮歷年節假日期間平均進出站客流量的特征。基于此,模型的輸入選取為:① 歷史某一年節假日前的平常日進出站客流量(包括節假日前2個月的工作日、周六周日日均進出站客流量);② 歷史某一年節假日期間的平均進出站客流量;③ 歷史次年節假日前的平常日進出站客流量(括節假日前2個月的工作日、周六周日日均進出站客流量)。模型的輸出選取為:歷史次年節假日期間的平均進出站客流量。
在預測過程中將分別針對每類站點建立進出站客流量預測模型,預測流程如下:
Step 1: 準備模型的輸入、輸出歷史數據。
Step 3:選取最小二乘支持向量機(LSSVM)的核函數。由于徑向基函數的應用范圍最廣,可以直觀反映2個數據的距離,因此本研究選取徑向基函數作為核函數。
Step 4:應用十折交叉驗證法選擇正則化參數C和核參數σ2。

Step6:根據Step5生成的預測函數預測未來年節假日的客流值,并對預測誤差進行評價分析;如果誤差較大則返回Step1,重新調整模型輸入和LSSVM參數再進行預測。
其中,正則化參數C的初始值設為100,尋優范圍設置為[e-1,e10];核參數σ2的初始值設為0.1,尋優范圍設置為[e-3,e8];誤差函數選取的是估計值與真實值的均方誤差,當前后2次尋優的均方誤差的減小量小于10-3時,結束尋優。預設誤差要根據樣本數據的特征而定。進出站客流量預測流程如圖2所示。
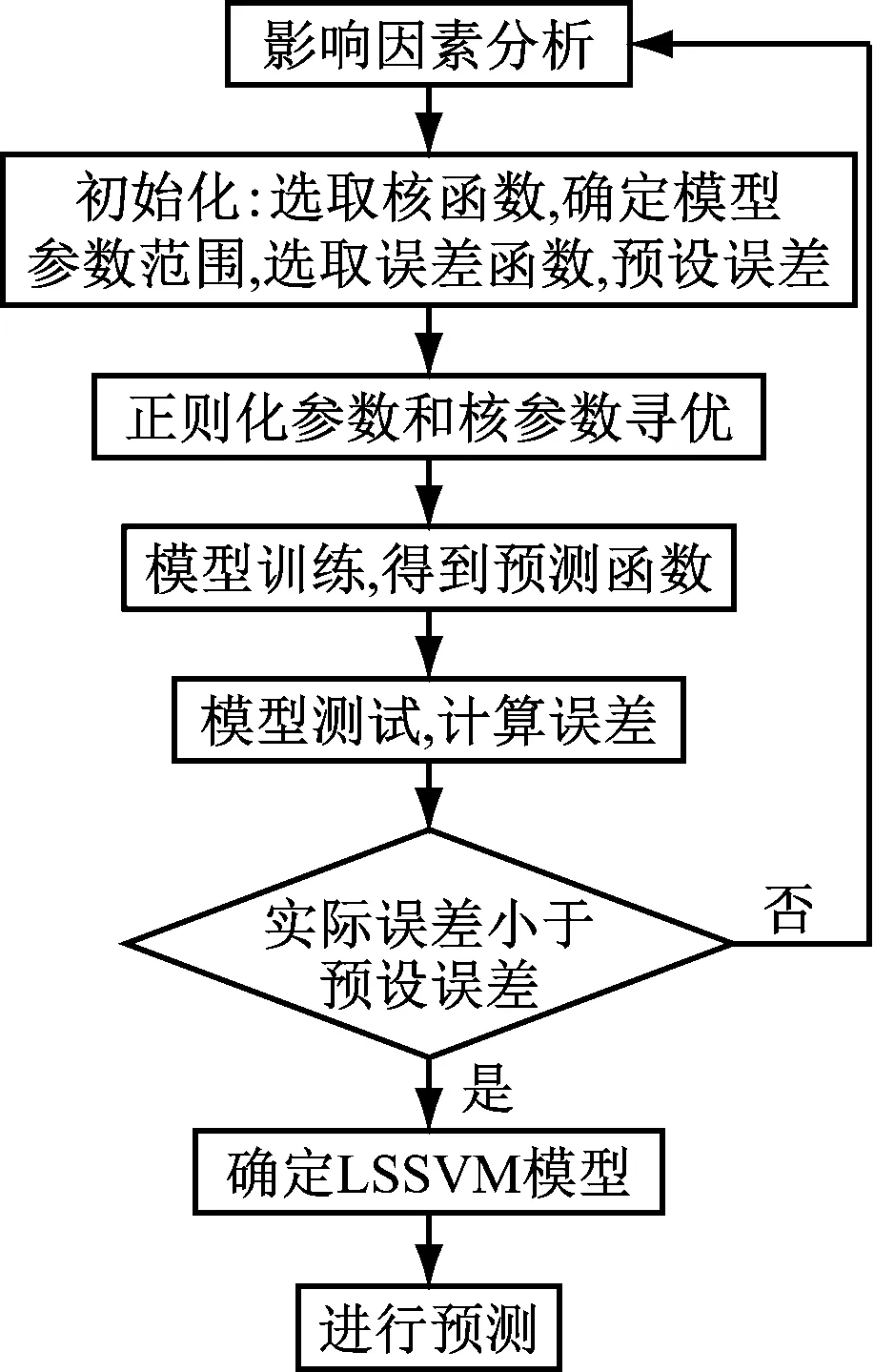
圖2 進出站客流量預測流程
2.2 模型參數標定
確定模型框架后,根據所預測的節假日歷年數據,標定預測模型的參數。支持向量機模型所需標定的參數包括:正則化參數C和核參數σ2。在實際應用中,一般采用十折交叉驗證法對參數進行標定。
以2014—2017年國慶假期的客流量歷史數據為例,進行模型參數標定,標定結果如表1所示。計算中先以2014—2016年國慶假期的客流量為歷史數據,并將正則化參數C的初始值設為100,核參數σ2的初始值設為0.1,采用十折交叉驗證法,計算2017年國慶假期客流量的預測值;然后將預測值與實際值進行對比后,修正正則化參數C和核參數σ2后,再次進行預測;迭代執行上述步驟,直到預測值與實際值誤差小于10-3。此外,考慮到在實際應用中,可能存在無法滿足誤差小于10-3條件的情況,因此將迭代次數限定為100次;當無法滿足誤差條件時,則以100次參數標定結果中,預測值與實際值誤差最小的一套參數作為最佳參數。
然后,對各類模型的樣本集進行訓練,以各類車站進站客流量的訓練擬合效果為例進行說明,如圖3所示,各類車站進站客流量預測模型的訓練擬合效果均較好。

表1 各類車站模型的最佳正則化參數C和核參數σ2

a) 商業類或景點類車站
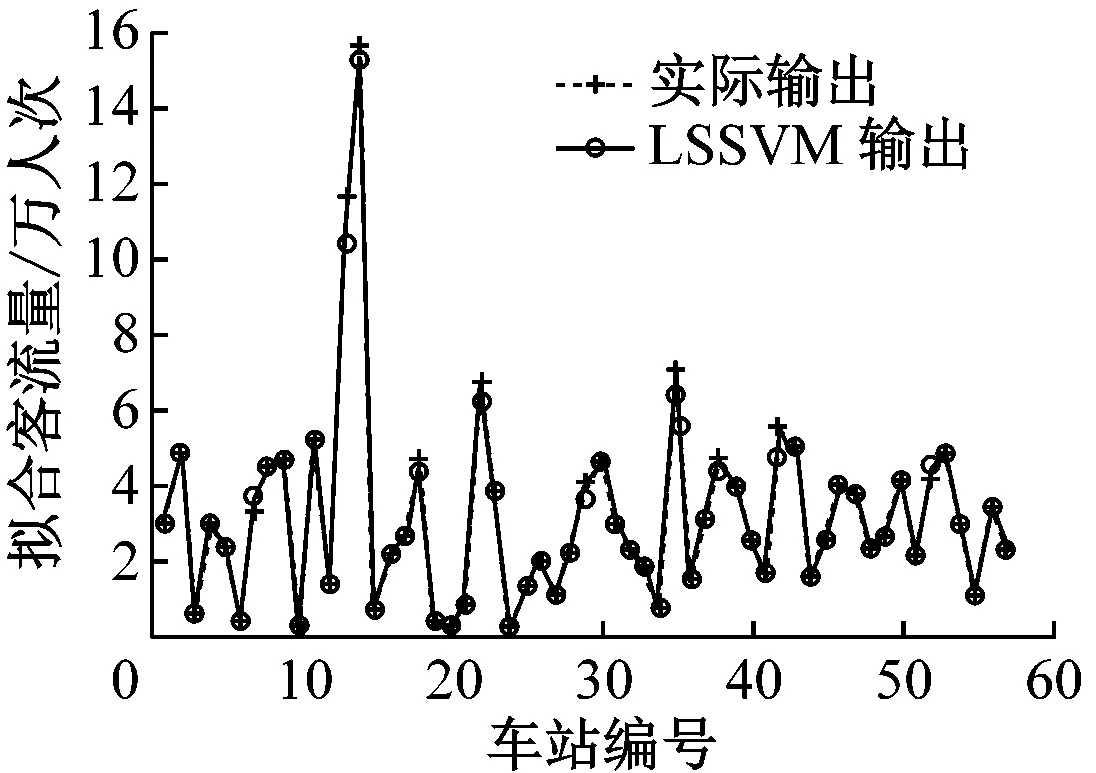
b) 其他類(市區站)
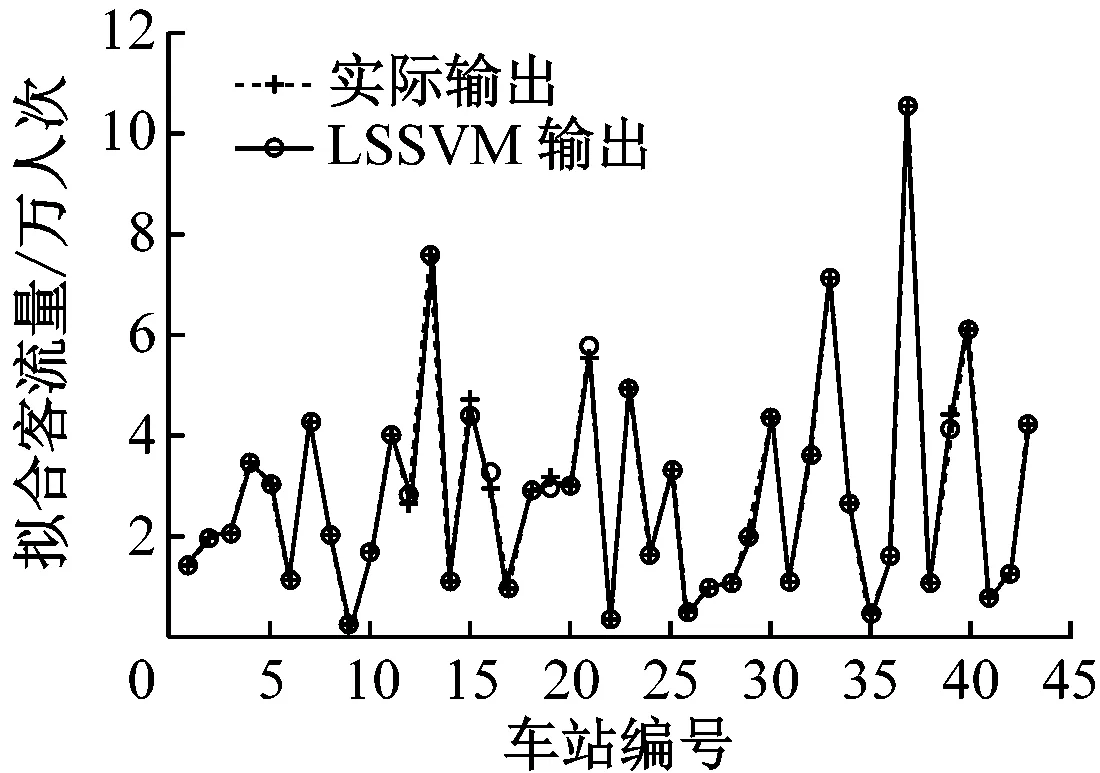
c) 其他類(郊區站)圖3 各類車站進站客流量的訓練擬合效果圖
2.3 模型驗證
為了檢驗模型的預測效果,本文以2014—2016年國慶假期的客流數據進行訓練,生成預測函數,進而預測2017年國慶假期的進站客流量,并與實際值相比較,分析模型的預測效果。圖4為各站點國慶假期平均進站客流量的預測值與真實值的對比圖。
由圖4可見,散點(實際值)大都集中在45°線(預測值)上,說明各個車站國慶假期平均進站客流量的預測結果較好。對各類車站國慶假期平均進出站客流量預測的平均相對誤差百分比進行統計,結果如表3所示。
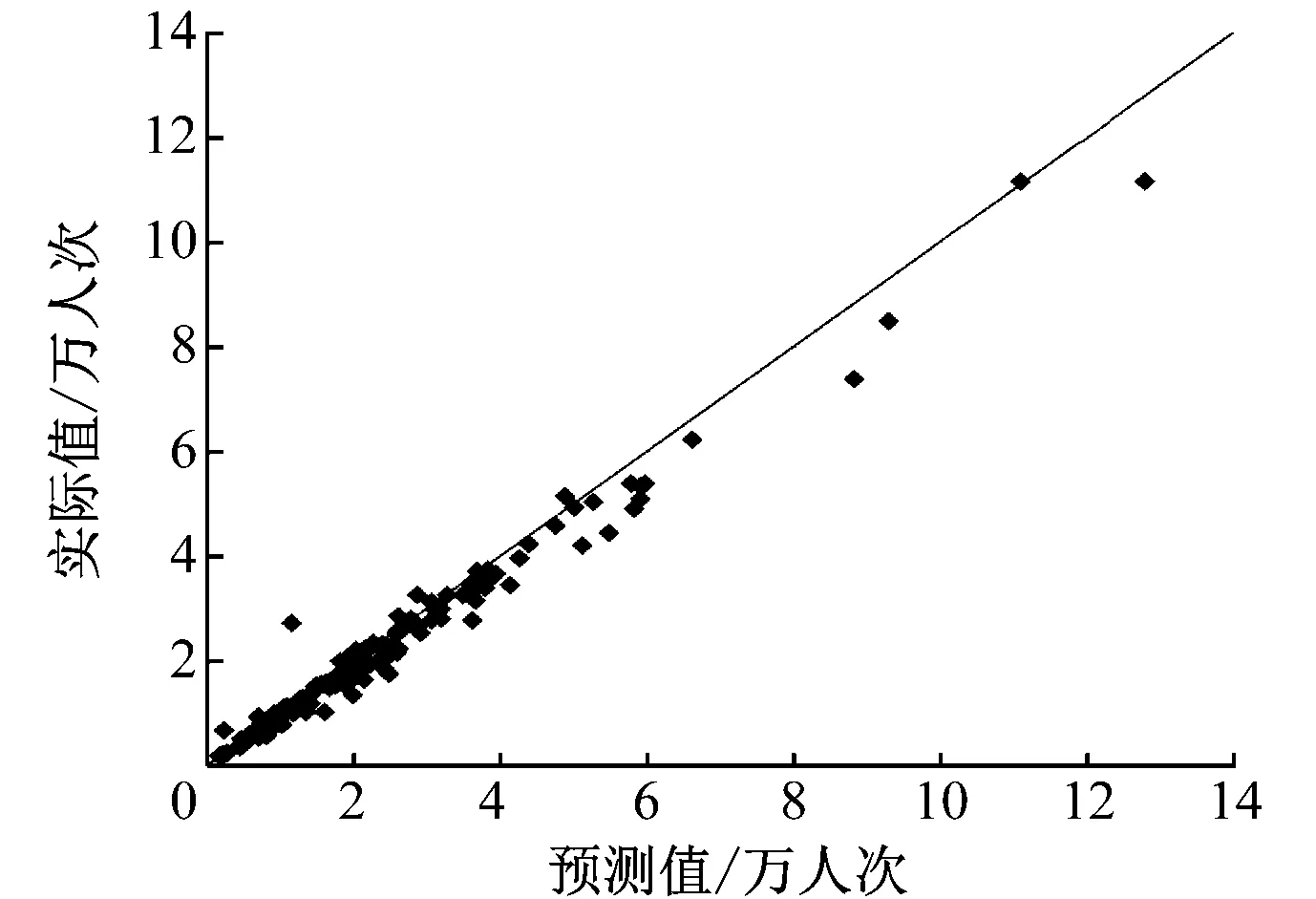
圖4 各車站國慶假期平均進站客流量的 預測值與實際值對比表2 國慶假期各類車站的客流預測平均相對誤差

車站類型預測誤差/%進站客流量預測出站客流量預測商業類或景點類7.705.43其他類(市區站)1.496.44其他類(郊區站)1.785.20
從表2可以看出,基于支持向量機建立的國慶假期平均進出站客流量模型的預測效果較好。進而,基于國慶假期平均進出站客流量的預測值、各車站每天進出站客流量與國慶假期客流量均值的比例數據庫,預測2017年國慶假期七天各站點的進出站客流量。每天的客流預測平均相對誤差百分比如表3所示。
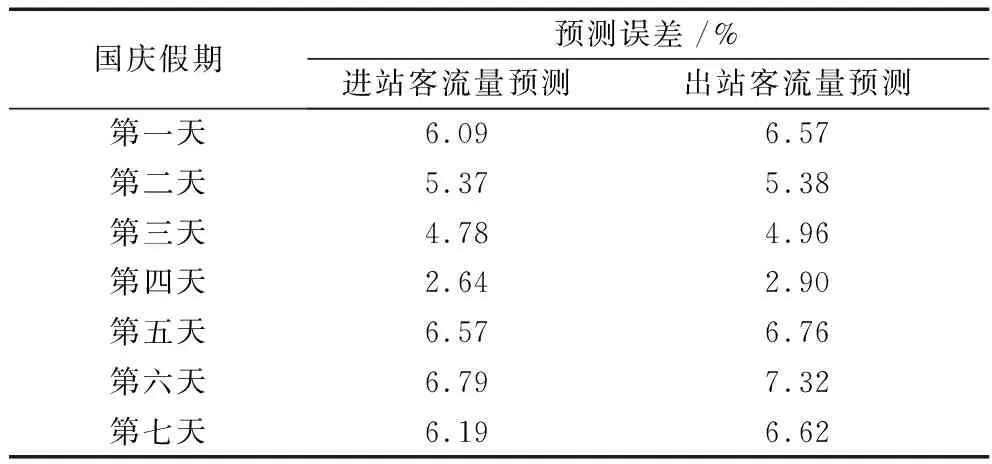
表3 2017年國慶假期各車站客流預測平均相對誤差
從表3可以看出,預測效果較好。進一步說明了基于該比例數據庫分別預測各節假日每天的進出站客流量是可行的。同理,可以建立節假日前一天各類車站的模型,預測節假日前一天各車站的進出站客流量。
3 結語
本文以城市軌道交通進出站客流為研究對象,通過研究分析節假日期間進出站客流特征,對車站類別進行合理劃分。然后,對模型的輸入與輸出樣式進行研究,并基于歷史數據確定樣本集,計算預測模型的最佳正則化參數和核參數,分別構建適用于節假日進出站客流預測的支持向量機模型。最后,基于所構建的支持向量機模型,以2014—2016年的國慶假期客流歷史數據,預測了2017年國慶假期各車站的進出站客流量,并通過與實際數據進行對比分析,檢驗了預測模型的精度。結果顯示,該模型預測的進出站客流量的絕對百分比誤差在8%以下,由此表明該模型具有較高的精度,可以為城市軌道交通運營組織管理工作提供重要的決策依據。