基于灰靶理論和磨粒濃度的磨損狀態自動識別

王慶維，王靜秋

(南京航空航天大學 機電學院，江蘇 南京 210016)

0 引言

磨損、腐蝕和疲勞是三種導致機械零部件失效的主要原因，而三者中磨損一項占了八成左右[1]。磨損不僅會消耗材料與能源，也會影響機械設備的可靠性。零件的磨損也會造成機械設備的工作效率和精度變低，導致能耗增加以及漏油、漏氣、噪聲等故障發生的概率增大。因此對機械設備進行監測，確定設備異常磨損的部位以及故障發生的原因，及時地對設備進行保養維修，避免故障的發生，減少停機造成的損失并保證工作人員的安全，對設備進行磨損工況監控和故障診斷都具有重要的意義。

在眾多設備狀態檢測和故障診斷方法中，油液檢測技術作為一種有效的工況監測方法已在各類機械設備上得到廣泛的應用。由于鐵譜圖像的復雜性，油液分析技術往往需要有經驗的技術人員，憑經驗來判斷機械的磨損狀態，不能做到磨粒的自動化識別[2]和設備磨損的自動判斷。于是在自動分析只能得到少量數據的情況下，灰色系統理論得到了應用。目前已有學者利用灰色關聯方法對磨損模式進行判別。而監測過程中，設備運行往往沒有標準模式，因此本文引入灰色系統理論中灰靶理論進行分析研究。

1 灰靶理論原理

灰靶理論(grey target theory)即灰模式理論是鄧聚龍教授提出的[3-6]，用于處理模式序列的灰關聯分析理論。

灰靶理論的計算是在沒有標準模式的條件下構造一個灰靶，即在任意的一組模式序列中，找出最靠近子命題目標值的數據構造標準模式，然后各待測模式與標準模式一起構造灰靶，則標準模式便是灰靶的靶心。然后將每一個指標的模式與標準模式進行比較，求出灰關聯度，最后由劃分的等級來確定評估等級。

灰靶理論包括兩部分：靶心度分析和貢獻度分析。靶心度計算步驟為：建立設備的標準故障模式；進行灰靶變換；計算灰關聯系數；計算靶心度；待識別模式的識別。灰靶貢獻度就是研究各性能指標對靶心度大小的影響。

1.1 靶心度計算

如果用序列來表示設備在i時刻的n個狀態參數值，那么稱該序列為設備狀態模式。基于灰靶理論分析方法，根據設備在m個時刻的故障狀態，建立設備的標準故障模式，然后將待識別的設備狀態模式{ωi(1)，ωi(2)，…，ωi(n)}與設備的標準故障模式進行關聯度分析，進而識別該設備的故障模式。

1) 建立標準故障模式ω0

設ωi為設備的第i次故障模式，ω(k)為設備狀態監測的第k個狀態參數序列，則按如下建立標準故障模式ω0。

ωi={ωi(1),ωi(2),…,ωi(n)}，

?ωi(k)∈ωi?k∈{1,2,…,n}，

i∈I={1,2,…,m}；

ω(k)={ω1(k),ω2(k),…,ωm(k)}，

?ωi(k)∈ω(k)?i=I∈{1,2,…,m}。

令POL(max)，POL(min)，POL(mem)分別為極大值性、極小值性和適中性極性。

那么稱序列ω0={ω0(1),ω0(2),…,ω0(n)}

為設備的標準故障模式。

2) 灰靶變換T

(1)

式中：j=J∈{1,2,…,P}，P是待識別的狀態模式總數。

當j=0時，有：

Tω0=x0={x0(1),x0(2),…,x0(n)}={1,1,…,1}

稱x0為標準靶心。

3) 灰關聯系數γ{x0(k),xj(k)}

(2)

式中：

Δ0j(k)=|x0(k)-xj(k)|=|1-xj(k)|，

j∈J={1,2,…,P}，k∈K={1,2,…,n}，ρ=0.5

4) 靶心度計算γ{x0,xj}

(3)

5) 設備狀態模式識別

按最小信息原理，靶心度的分檔應該均衡分布，所以有[0.1，0.2]，[0.2，0.3]，[0.3，0.4]，[0.4，0.5]，[0.5，0.6]，[0.6，0.7]，[0.7，0.8]，[0.8，0.9]， [0.9，1] 。

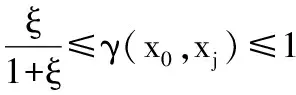
取ξ=0.5，則γ(x0,xj)≥0.333 3

所以，0.333 3以下各檔無意義。根據設備故障的描述系統，對設備故障的描述可分為：正常磨損、輕微磨損、嚴重磨損、磨損十分嚴重。于是將靶心度分為如下等級：

γ(x0,xj)=1，理想狀態，該設備完全正常；

γ(x0,xj)=[0.8，1]，正常磨損；

γ(x0,xj)=[0.7，0.8]，輕微磨損；

γ(x0,xj)=[0.5，0.7]，嚴重磨損；

γ(x0,xj)<0.5，磨損十分嚴重。

最后根據xj的靶心度γ(x0,xj)的大小，計算出設備在時刻j的狀態與標準狀態模式的接近程度，從而進行設備運行狀態判斷。

1.2 灰靶貢獻度

模式由指標構成，模式的靶心度大小與指標有關。所謂灰靶貢獻度就是研究各性能指標對靶心度影響程度的一種數學方法[7]。

令@GRF為灰關聯因子集，

@GRF={x(k)|k∈K∪{0},K={1,2,…,n},

x(0)=(x1(0),x2(0),…,xm(0)),

?xi(0)∈x(0)?xi(0)=Tlωi(0),

Tu、Tl和Tm分別為極大值性、極小值性和適中性極性。稱x(k)為第k個貢獻因子，稱@GRF為貢獻因子集。

令ΔGR為貢獻因子集對應的灰關聯差異信息空間，

ΔGR=(Δ,ζ,Δmax(0,k),Δmin(0,k))，

Δi(0,k)=|xi(0)-xi(k)|，

則ΔGR上的灰關聯系數γ(xi(0),xi(k))：

(4)

稱為k指標在i點(模式)的貢獻系數；

灰關聯度γ(x(0),x(k))：

(5)

稱為k指標的貢獻度。

1.3 加權公式的構造

在求得各指標的灰靶貢獻度后，取它們的平均值并記做γmem。則該值所對應的權值應為1/n。以各指標貢獻度與貢獻度平均值的差為依據，構造如下公式，通過差值所占平均值的比例來確定權值。

(6)

式中，當γ(i)>γmem時，取正號；當γ(i)<γmem時，取負號。

最后引入加權系數之后的靶心度計算公式為：

(7)

2 基于灰靶理論和磨粒濃度的磨損狀態的自動識別

2.1 磨粒濃度的獲取

鐵譜分析技術是一種通過分析鐵譜圖像的磨粒尺寸、數量、形貌和成分等特征[8-9]去識別機械狀態的技術。在眾多特征中，磨粒尺寸和數量是圖像自動化處理最容易得到的，同時也是最直觀反映設備磨損狀態的特征。

磨粒尺寸指的是磨粒長軸尺寸。長軸為圖1磨粒等效橢圓圖中的a。于是可以通過等效橢圓的方法，得出磨粒的尺寸。

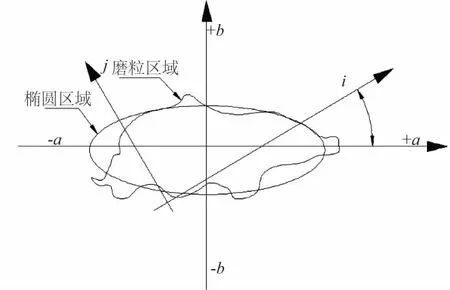
圖1 磨粒等效橢圓圖

首先確定磨粒中某個像素點所處磨粒的尺寸，然后把該像素點加入到對應的尺寸范圍內，通過該方法得到所有磨粒中像素點的尺寸范圍，并計算出各尺寸范圍的磨粒濃度。以各尺寸的磨粒濃度為指標建立標準模式。磨粒濃度為鐵譜圖像中各尺寸范圍內的磨粒面積與總磨粒面之比。

本文的分析對象為某公司型號Y7001的設備。表1為6幅鐵譜圖像通過上述的方法得出的磨粒濃度表，通過表1建立標準模式，來識別表2中的待檢測鐵譜圖像的磨損狀態。圖2和圖3為該設備的不同時間的鐵譜圖像，對應著表2中的樣本1和樣本2的磨粒濃度。通過圖2和圖3，知道圖2設備所處的時間，圖像中都是比較小的磨粒，沒有出現較大磨粒，所以認為設備為正常磨損，只需要繼續監測設備狀態。而圖3的圖像中不僅有較小的磨粒，而且出現了較大的磨粒，或者說設備出現了不異常磨損，需要對設備進行檢查和維修。

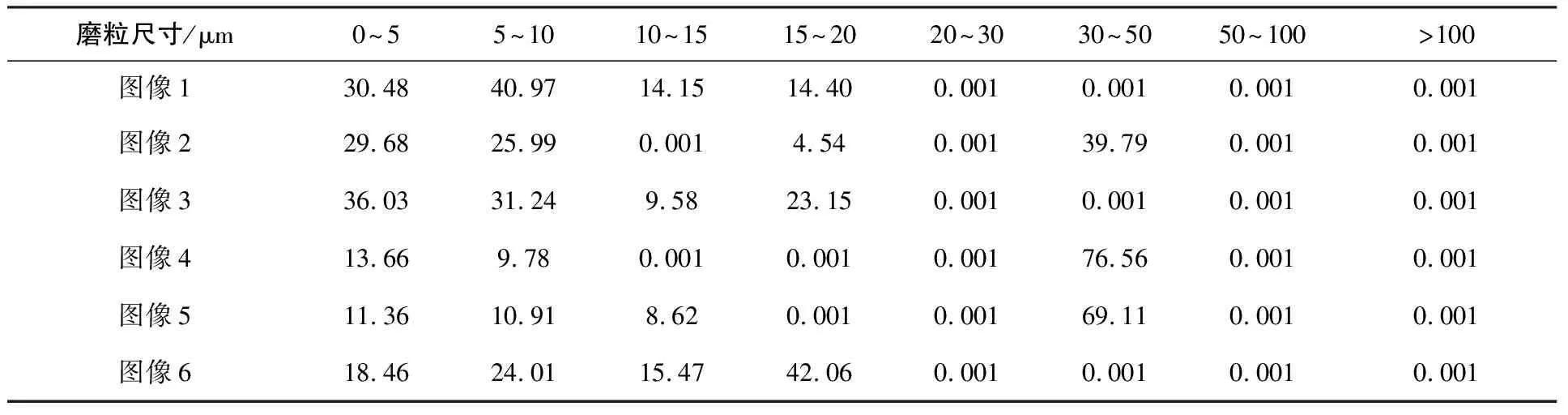
表1 標準模式的磨粒濃度表

表2 待檢測圖像磨粒濃度表

圖2 樣本1圖像

圖3 樣本2圖像

2.2 靶心度計算

1) 建立標準模式

ω0(1),ω0(2),ω0(3)采用POL(mem)，其余使用POL(min)。

ω0(1)=avg{30.48,29.68,36.03,13.66,11.36,18.46}=23.28

同理：ω0(2)=23.82ω0(3)=7.97

ω0(4)=0.001ω0(5)=0.001

ω0(6)=0.001ω0(7)=0.001

ω0(8)=0.001

則標準模式：

ω0={ω0(1),ω0(2),…,ω0(8)}={23.28,23.82,7.97,0.001,0.001,0.001,0.001,0.001}

2) 灰靶變換

對待識別模式進行灰靶變換。

(8)

根據式(1)計算可得:

{0.338 3，0.971 0，0.834 8，1，1，1，1，1}

{0.464 6，0.297 8，0.899 2，1，0，0，1，1}

3) 靶心系數及靶心度的計算

樣本1：

γ{x0(1),x1(1)}=0.333 3

γ{x0(2),x1(2)}=0.919 5

γ{x0(3),x1(3)}=0.667 0

γ{x0(4),x1(4)}=1

γ{x0(5),x1(5)}=1

γ{x0(6),x1(6)}=1

γ{x0(7),x1(7)}=1

γ{x0(8),x1(8)}=1

靶心度：

樣本2：

γ{x0(1),x2(1)}=0.482 9

γ{x0(2),x2(2)}=0.415 9

γ{x0(3),x2(3)}=0.832 3

γ{x0(4),x2(4)}=1

γ{x0(5),x2(5)}=0.333 3

γ{x0(6),x2(6)}=0.333 3

γ{x0(7),x2(7)}=1

γ{x0(8),x2(8)}=1

靶心度：

2.3 灰靶貢獻度

根據表1，得出貢獻因子集由8個序列構成：

ω(0)=(ω1(0),ω2(0),…,ω8(0))={1,2,3,4,5,6}

現給出參照表1所得磨粒各尺寸的貢獻度：

γ=(0.613 6,0.697 7,0.670 9,0.670 9,0.478 7,0.642 4,0.478 7,0.478 7)

2.4 加權公式構造

根據式(6)，經計算所得的權值為:

q1=0.129 6，q2=0.147 4，q3=0.141 8，q4=0.141 8，

樣本1：

樣本2：

通過樣本1和樣本2的靶心度與設備狀態級比較，可知設備在樣本1的靶心度所處的范圍為γ(x0,xj)=[0.8，1]，所以設備磨損狀態為正常磨損；而設備在樣本2的靶心度所處的范圍為γ(x0,xj)=[0.5，0.7]，所以設備磨損狀態為輕微磨損狀態。由樣本2的靶心度，可預測設備出現了異常的磨損情況，建議對設備的該時刻之后進行檢測。實驗得出的結果與設備實際檢測的情況是一致的。

3 結語

本文基于灰靶理論和磨粒濃度的磨損狀態的自動識別，經算例分析驗證了其有效性，可應用于設備磨損狀態的自動識別。通過分割算法得到準確的鐵譜圖像的各尺寸磨粒濃度，為模型提供了準確的數據依據；利用貢獻度優化指標權重，考慮不同的尺寸濃度的影響，考慮的因素更加全面，也證明了靶心度能反映設備的磨損狀態。本文基于灰靶理論和磨粒濃度的磨損狀態的自動識別，實現了從鐵譜圖像到設備磨損狀態的自動識別，對實際的決策評估過程具有一定的指導和借鑒意義。