基于VaR模型與ES模型風險度量分析

賈振方

[提要] 隨著我國金融市場的飛速發展，資本市場的不斷完善，金融風險的科學化監測與管理顯得尤為重要。本文簡要介紹VaR模型與ES模型的概念、定義及計算方法，分別選取正常情況下與非正常情況下的上證指數進行實證分析，并從準確性與精確度兩個維度對統計結果進行回測檢驗。最后得出結論：ES作為一種風險度量工具，在準確度與精確性方面與VaR相比具有無可替代的優勢，它是一種更為精確而實用的風險度量工具，對我國金融市場風險管理具有重要的意義。

關鍵詞：風險度量；VaR模型；ES模型；風險管理

中圖分類號：F830 文獻標識碼：A

一、引言

金融風險指的是將一定量的金融資產進行投資，在未來時間內預期收入遭到損失的不確定性。為了有效地避免損失，越來越多的人意識到了風險管理的重要性。然而，進行風險管理的首要任務就是對風險進行準確的度量，因此國內外學者在此方面進行了大量的研究。Markowitz（1952）首先提出運用均值—方差研究投資組合中的風險問題。因為方差能夠很好地刻畫資產的價格波動情況，所以很快就得到了推廣和使用。隨著人們對風險的進一步研究發現，用方差的大小表示風險并不十分恰當。于是Bawa（1977）提出了下偏距理論，認為風險的度量范圍應該是向下偏離的波動，而不是整個收益的波動。風險的下偏距是一種很好的風險衡量指標，它不僅解決了方差度量雙邊風險的問題，而且還放松了對二次效用函數的限制要求。無論是均值-方差理論還是下偏距理論，他們都是傳統的金融風險度量工具，都是建立在橢圓分布的假設前提下度量風險的。

然而，經驗數據表明，資產收益密度曲線一般是非對稱、非正態的，不符合橢圓分布的假設前提。在此背景下，G30集團在1993年研究金融衍生品種基礎上首次提出VaR風險度量方法，1994年J P.Morgan公布了VaR的經典計算方法——RiskMetrics方法。由于VaR可以將抽象的風險具體化、定量化，能夠直觀定量的計算出金融機構所面臨的風險，既能用于風險控制，又能用于業績評估，還可以很好地估算風險性資本，所以一經問世就得到業內人士普遍認可。

然而，VaR也有以下兩點局限：（1）不滿足Artzner、Delbaen等（1999）提出的一致性風險度量中的次可加性；（2）VaR只關注收益的分位數，卻忽略了極端情況下的尾部風險。為了解決以上問題，Artzner等提出基于ES模型的風險度量方法。ES不僅滿足風險度量中的一致性要求，而且還關注投資組合的尾部風險。2012年5月3日巴塞爾協議Ⅲ中，巴塞爾委員會明確提出要逐步淘汰VaR，并采用ES作為替代指標。

二、模型的理論基礎

（一）VaR模型。風險價值，即在一定的持有期間內和給定的置信水平下，某一金融工具或其組合在未來資產價格波動下所面臨的最大損失額（率）。例如，某金融機構某項投資一周的99%的VaR值是100萬元，表明該金融機構可以以99%的概率保證在未來的一周內該項投資由于價格變動而導致的最大損失不會超過100萬元。

用數學公式定義為：prob（△>VAR）=1-c （1）

其中，△r表示資產組合在持有期間△t內的收益（損失），c表示置信區間，VaR表示在置信水平c下的風險價值。

（二）ES模型。預期不足，又名條件風險價值（CVaR），也可稱為尾部預期損失（ETL）。ES風險度量是針對VaR風險度量的局限性提出的又一種風險度量方法，相比VaR而言，有更優的統計特性。ES表示的是，在預先給定的分位數下，小于此分位數所對應收益的尾部損失的平均值，是對VaR風險度量方法的有益補充。

（三）VaR和ES的計算方法。VaR和ES的計算方法有很多，其中最主要的有三種：方差—協方差法、歷史模擬法和蒙特卡洛模擬法。方差—協方差法假定市場因子的變化服從多元正態分布的，利用正態分布的統計特性來計算VaR值與ES值；歷史模擬法是最簡單的非參數估計方法，它假定歷史將會重現，市場因子未來的變化情況與歷史上的波動情況完全一致，可以拿過去的收益分布曲線模擬未來的收益分布曲線，再依據定義確定VaR值與ES值；蒙特卡羅模擬法的基本思路是分析歷史風險因子的波動規律，利用該規律產生風險因子未來將要波動的大量可能路徑，通過模擬分布可以獲得較為接近真實分布的近似估計，從而預測出 VaR 值和 ES 值。

三、實證分析

（一）數據選擇與處理。上證指數是我國第一個股票指數，與深證成指或滬深300指數相比，它包含的股票數量豐富，歷史悠久，更能反映我國股市的波動情況。因此，本文選取2005年1月4日（第一個交易日）至2008年12月31日（最后一個交易日）上證指數作為非正常情況下的實證數據。其中，2005年1月4日至2007年12月29日的725個數據為樣本內數據，2008年246個交易日數據為樣本外數據。另外，選取2002年1月4日至2005年12月30日上證指數作為正常情況下數據。其中，2002年1月4日至2004年12月31日的721個數據為樣本內數據，2005年242個交易日數據為樣本外數據。首先對數據進行處理：Ln（Pt/Pt-1），其中Pt指的是第t日的上證指數收盤價，Pt-1指的是t-1日的上證指數收盤價。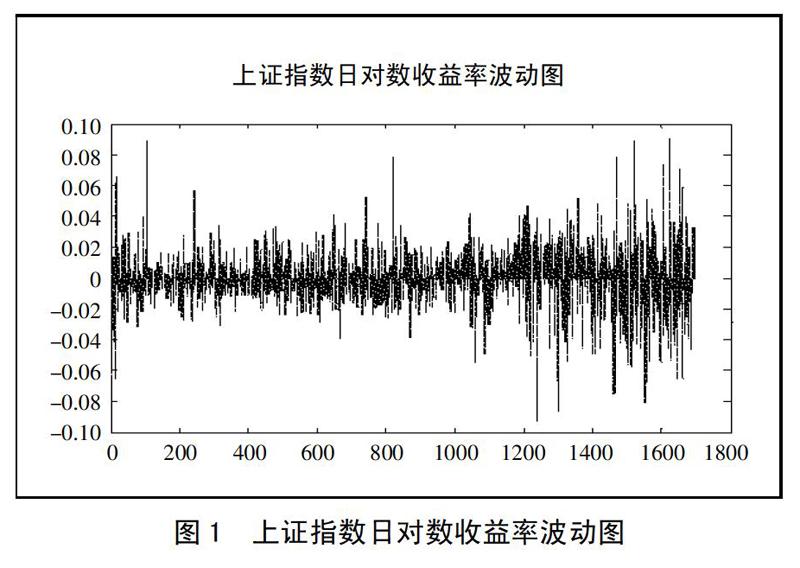

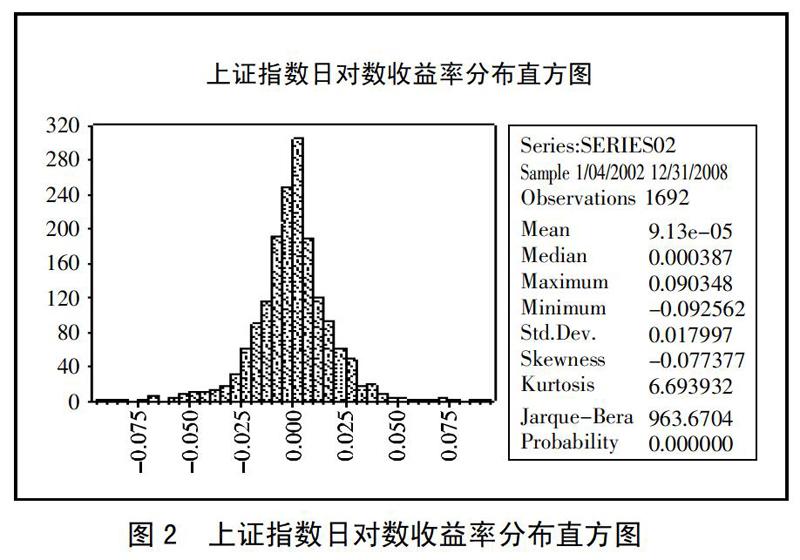
（二）描述性統計分析。分別作出上證指數日對數收益率基本統計分析的時間序列圖、直方圖。由圖1可知，上證指數日對數收益率存在著明顯的時變性與集聚性。學者普遍認為在風險度量的實際操作中考慮資產收益分布曲線的非對稱是非常重要的，如峰度、偏度等指標。由圖2可知，上證指數日對數收益率偏度<0，說明該分布左偏，峰度>3，說明該分布存在尖峰肥尾現象，不符合正態分布。（圖1、圖2）

（三）研究方法與計算過程。考慮到上證指數數據易于獲取、日對數收益率呈現出尖峰肥尾的特性，最終采用簡單易懂的歷史模擬法來完成VaR值與ES值的計算（通過MATLAB2013實現）。

正常情況下：

1、令A=X1，X2，X3…Xn，其中，Xi（i=1，2，3…n）是2002年1月4日至2004年12月31日的n個交易日的上證指數日對數收益率。

2、將X1，X2，X3…Xn按照從小到大的順序依次排列起來，可以得到一個新的數列：B=X1′，X2′，X3′…Xn′。

3、計算c%分位點對應的最壞收益序列數m，若m為整數，則2005年1月4日的Va值表示為：VaR1（c%）=Xm′；若m不是整數則利用插值法求解VaR1（c%）。

4、計算出VaR1（c%）左側的均值即為ES1（c%）。

5、用2005年1月4日的真實日對數收益率Y1替換2002年1月4日的對數收益率X1，得到新數列Y1，X2，X3…Xn，然后循環執行步驟（1）（2）（3）（4）（5）依次得到2005年1月5日、6日至2005年12月30日的VaR（c%）、ES（c%）。

6、將所得的VaRi（c%）、ESi（c%）分別與第i日真實的上證指數日對數收益率比較，并統計失敗率。

非正常情況下的數據計算與之相同。

（四）回測檢驗。對測量結果的檢驗主要有兩個方面：一是準確性。可以依據不同置信水平下的失敗率是否小于1-c來判斷；二是精確度。可以依據Kupiec失敗率檢驗方法來測定。Kupiec（1995）失敗率檢驗方法的操作思路：運用Kupiec失敗率檢驗回測結果的精確度也即是檢驗真實的失敗率在給定的置信水平下是否顯著不等于期望失敗率。可以將失敗率檢驗的二項式結果看成一系列獨立的伯努利實驗，在給定的置信水平c下的期望失敗率為p*=1-c，真實失敗率為p=N/T（T為樣本數，N為失敗次數），零假設為在給定置信水平下真實失敗率等于期望失敗率，即p=p*，備選假設為在給定置信水平下真實大敗率等于期望欠敗率，即p=p*，備選假設為在給定置信水平下真實失敗率顯著不等于期望失敗率，即p≠p*。Kupiec提出似然比率檢驗：

（五）實證結果與分析。根據計算流程，可以分別得到2005年242個交易日和2008年246個交易日在不同置信水平下的VaR值與ES值，其最終的統計結果如表1所示。由表1可知，在正常情況下VaR的LR統計量均小于臨界值，真實失敗率與預期失敗率基本相同；ES在不同置信水平下的真實失敗率小于預期失敗率，滿足準確性要求。但是，ES在95%的置信區間下LR統計量大于臨界值（7.627>3.841），而且不同置信區間下的真實失敗率均遠低于預期失敗率，精確度較差。由此可知，正常情況下VaR與ES均可作為我國股市風險的測量工具，且VaR略好于ES。當然，對于風險厭惡型的投資者或者對資金安全程度要求較高的商業銀行而言，ES依然是一個不錯的選擇。（表1）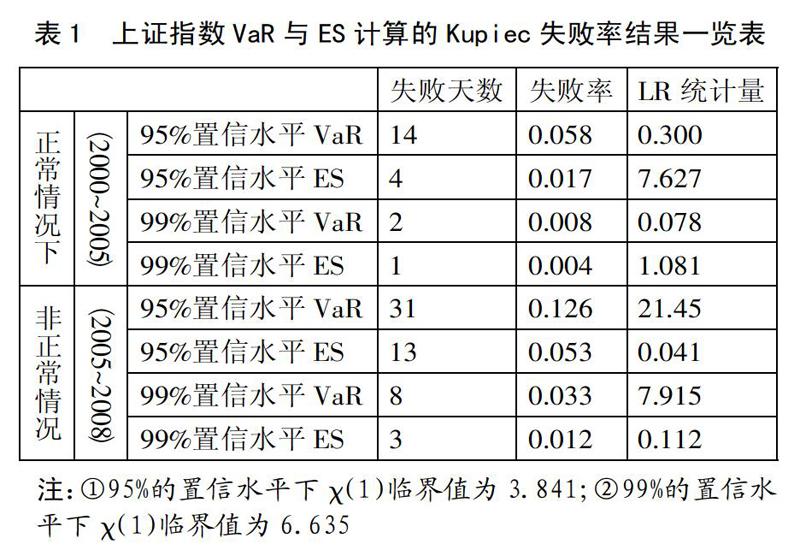

然而，在非正常情況下，VaR存在嚴重低估風險的情況，其真實失敗率均是預期失敗率的2～3倍，此時的VaR無論是在準確性上還是精確度上，測量屬性都比較差，不建議使用。而ES的失敗率在可接受的誤差范圍內，所以非正常情況下應選擇表現良好的ES測量風險。

四、結論

從理論上可知，一方面ES滿足一致性風險度量的所有條件，而VaR卻不滿足其中的次可加性；另一方面ES反映了尾部均值風險，既能有效地減少異常情況帶來的不利影響，又能及時反映市場突發風險。從實證可知，在正常情況下VaR與ES均可作為風險測量工具供不同風險偏好的投資者使用。但是，在非正常情況下，ES無論在準確性上還是精確度上都遠遠超過VaR，是一種更優良的風險測量工具。

綜上所述，ES作為一種風險度量工具在準確度與精確性方面與VaR相比具有無可替代的優勢，它是一種更為精確而實用的風險度量工具。當然，因為風險本身所具有的復雜性與多變性，ES不可能在任何情況下測量任何風險都會保持其優良的測量屬性。但總體而言，其在理論上與實踐上均有著不錯的表現，ES的推廣使用對我國金融市場的風險管理具有重要的意義。

主要參考文獻：

[1]Markowitz H.Portfolio Selection[J].Journal of Finance，1952.7（1）.

[2]Bawa V S，Lindenberg E B.Capital market equilibrium in a mean-lower partial moment framework[J].Journal of Financial Economics，1977.5（4）.

[3]梁建峰，陳健平，劉京軍.基于Copula-GARCH方法的LPM套期保值研究[J].系統工程學報，2011.26（5）.

[4]Artzner P，Delbaen F，Eber J M，et al.Coherent Measures of Risk[J].Mathematical Finance，1999.9（3）.

[5]Acerbi C，Tasche D.Expected Shortfall：A Natural Coherent Alternative to Value at Risk[J].Economic Notes，2002.31（2）.