基于改進VMD與包絡導數能量算子的滾動軸承早期故障診斷

任學平， 李 攀， 王朝閣， 張 超

(內蒙古科技大學 機械工程學院，內蒙古 包頭 014010)

滾動軸承是機械設備中應用最廣泛的零件之一，它為旋轉的軸及軸上的零件提供穩定的支撐，并保持軸的正常工作位置和旋轉精度。當軸承出現早期故障時，旋轉軸會出現抖動，會影響到整個設備的工作精度和生產效率，如果不能及時識別和更換軸承，軸承故障會不斷加深擴大，使整個設備癱瘓，嚴重時甚至會發生災難性事故。因此，準確及時地識別軸承早期故障，能夠實現對設備的早期預警，可以在不破壞設備運行狀態的情況下，制定合理、科學的維護方式，從而避免災難性事故的發生[1-3]。

當軸承出現局部損傷時，相互接觸的元件在受載的運行過程中會相互撞擊產生周期性沖擊，從而激起軸承系統的高頻固有振動[4]，產生調制信號，軸承的不同元件產生損傷會出現不同的故障特征信息。而軸承故障產生的初期，低頻段的故障特征往往伴有機械系統中其他干擾信號，導致故障沖擊極其微弱，故障特征頻率提取困難。如何準確地提取故障特征頻率成為識別軸承早期故障的關鍵。

變分模態分解(Variational Mode Decomposing，VMD)[5]可自適應地將故障信號中高頻調制信息分離出來，并且非遞歸式的分解方式避免了遞歸式分解帶來的分解終止條件的確定和邊界效應等問題[6]。文獻[7]用VMD與Teager能量算子結合的診斷方法，在確定分解層數k值時，采用中心頻率觀察法，結果取得了滿意的效果。文獻[8]采用粒子群算法優化分解層數k值，準確提取了軸承故障特征。本文提出了一種能量差曲線法，將原始信號能量與分量的能量之差作為評價參數，選取能量差最小時的k值作為VMD最佳分解層數。

故障診斷中Teager能量算子與Hilbert變換相比較在信號的解調分析中具有一定的優勢[9]，Teager能量算子首先在聲音信號非線性分析處理中被提出[10]，并成功分析了調制信號。文獻[11]將Teager用于軸承故障診斷中，利用Fourier變換得到能量譜，準確識別了軸承故障特征信息。文獻[12]將Teager與EMD(Empirical Mode Decomposition)分解相結合，成功提取了故障特征頻率。2014年，O’Toole等[13]提出包絡導數能量算子。它是一種新的解調方法并且比Teager能量算子優越，該方法提高了Teager能量算子的性能，能夠在較強的噪聲環境下對信號進行準確地解調分析[14]。

在實際工況中，軸承早期故障特征通常被各種干擾信號和噪聲所淹沒。改進VMD方法對早期故障信號進行處理后，利用峭度準則選取的敏感分量中仍然存在部分噪聲，而包絡導數能量算子在解析信號時，具有一定的降噪效果，將兩者結合，提出了改進VMD與導數包絡能量算子的滾動軸承早期故障診斷方法，并通過仿真信號和實驗數據對本文方法的有效性進行驗證。

1 基本理論介紹

1.1 變分模態分解原理

VMD算法是通過迭代計算搜尋變分模態模型的最優解，從而確定每個本征模態分量的中心頻率及帶寬，進而可以將信號的頻率實現自適應剖分和各分量的有效分離[15]。

假設VMD分解的各個本征模態分量都是具有中心頻率的有限帶寬，將信號分解為k個本征模態函數uk(t)，使得模態分量的估計帶寬之和最小，約束條件為各模態分量之和與輸入信號f相等，具體如下：

(1) 本征模態函數uk(t)可以看成調制信號，對uk(t)進行Hilbert變換，得到其解析信號。令解析信號與e-jωkt相乘，將每個uk(t)的頻譜調制到相應的基頻帶。

(1)

(2) 通過對平移后解調信號梯度的平方L2范數，估計各模態信號帶寬，得到受約束的變分問題為

(2)

式中:{uk}為VMD分解的模態分量;{ωk}為各模態分量的中心頻率。

在變分問題中，引入二次懲罰因子α和拉格朗日懲罰因子求取最優解。

(3)

采用乘法算子交替方向法(Alternating Direction Method of Multipliers,ADMM)求得擴展拉格朗日的‘鞍點’，解決以上非約束性變分問題，將信號分解為k個本征模態分量。

在VMD分解信號時，需要預先對本征模態分量的分解個數k值進行設定。在分解實際信號時，由于噪聲嚴重，信號多變復雜，導致分解層數無法確定。在此提出一種能量差曲線法，以原始信號與全部分量的能量差為依據，確定分解層數k值，為了保證信號分解的完整度，將能量差最小的k值作為最佳分解層數，具體步驟如圖1所示。

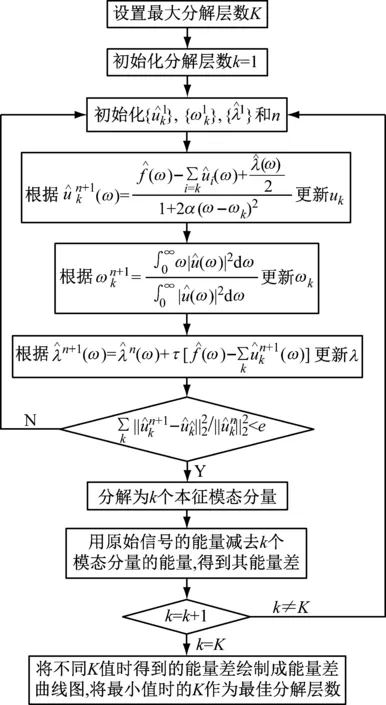
圖1 改進VMD流程圖

1.2 包絡導數能量算子

對于任何連續信號x(t)，Teager能量算子被定義為一個二階微分方程

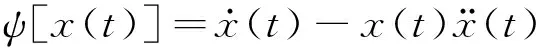
(4)

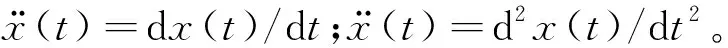
對于信號x(t)=Acos(ωt+φ)，ψ[x(t)]=A2ω2，這是Kaiser從機械系統的簡諧運動能量算法中得到的一種頻率加權能量算法。

對于一般的調制信號x(t)被定義為

X(t)=x(t)+jH[x(t)]

(5)

瞬時能量的典型算法是對信號的幅值進行平方

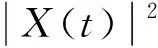
(6)

式中:H[x(t)]是對x(t)進行希爾伯特變換。信號的瞬時能量是根據振幅進行量化，如式(7)所示

S[Acos(Aω+φ)]=A2

(7)

式中:省略了任何關于頻率的信息。

同Teager能量算子方法相似，包絡導數算子通過選擇導函數作為加權濾波器，應用傅里葉變換的性質

(8)

定義包絡導數能量算子為

(9)

包絡導數能量算子和Teager能量算子相似，在定義的第一部分是相同的，不同在于第二部分，兩者的不同在頻域中能夠明顯的表現出來

*X(ω)

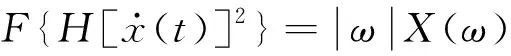
(10)

式中:*為卷積運算。

式(9)的包絡導數能量算法是對連續信號進行定義的，對于離散信號x(n)，同Teager能量算子一樣，采用差分代替微分，不同的是Teager能量算子采用的是向前差分法，包絡導數算子采用的是中心差分法，則包絡導數能量算子離散形式為

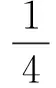
h(n+1)h(n-1)]

(11)

1.3 基于改進VMD與包絡導數能量算子的故障診斷流程

本文將改進后的VMD與包絡導數能量算子結合，提出了基于改進VMD與包絡導數能量算子的早期故障診斷方法。首先利用改進后的VMD將原始信號分解為k個模態分量，然后依據峭度準則選取敏感分量進行信號重構，最后應用導數包絡能量算子對重構信號進行解調，得到其能量譜，根據軸承數據算出故障特征頻率，判斷軸承故障。

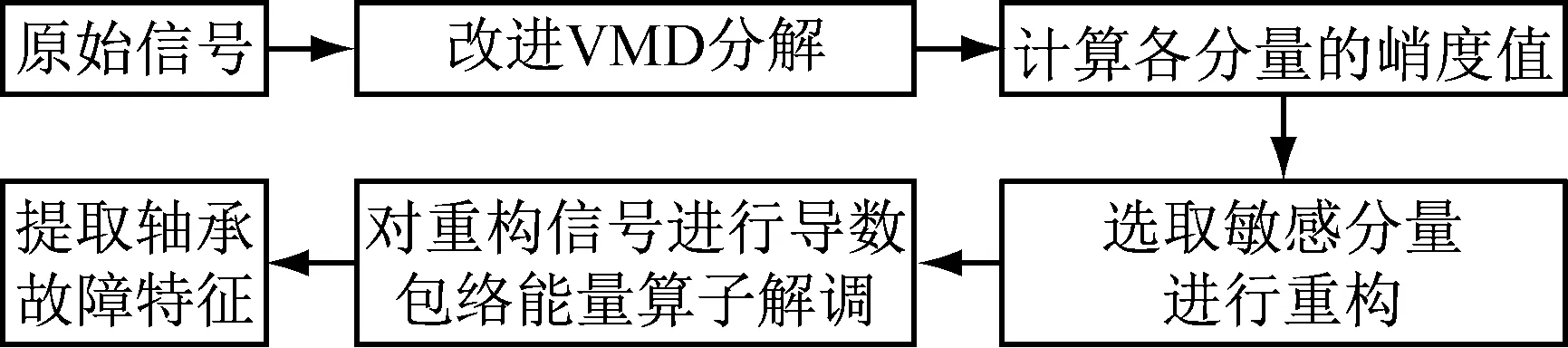
圖2 軸承早期故障診斷流程圖

2 仿真信號分析

為了驗證該方法的有效性，建立滾動軸承局部故障特征的仿真模型，對其進行改進后的VMD分解，再根據峭度準則選取敏感分量進行重構，最后對重構后的信號進行包絡導數能量算子解調，從能量譜中識別故障特征。

設定軸承故障為每轉產生一次沖擊，建立的勻轉速軸承故障模型為[16]

(12)

式中:幅值A為1;衰減系數ξ為1 000;共振頻率為3 000 Hz;故障特征頻率為f=1/T=180 Hz，采樣頻率fx為12 000 Hz，分析所用采樣點數為6 144點，沖擊信號的時域波形圖如圖3(a)所示。n(t)表示添加為高斯白噪聲，仿真信號波形如圖3(b)所示。

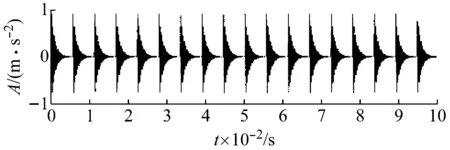
(a) 時域沖擊信號

(b) 染噪信號

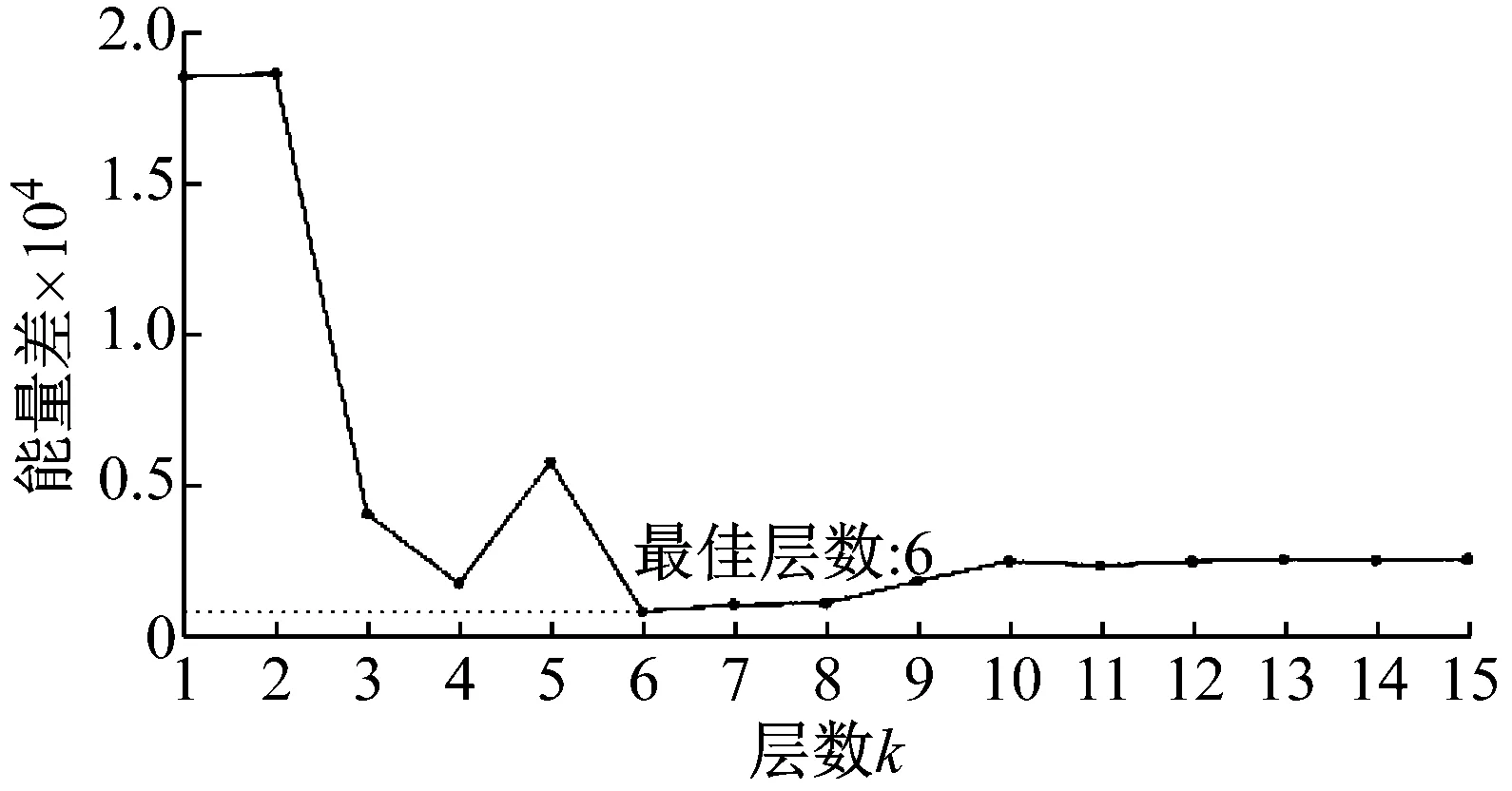
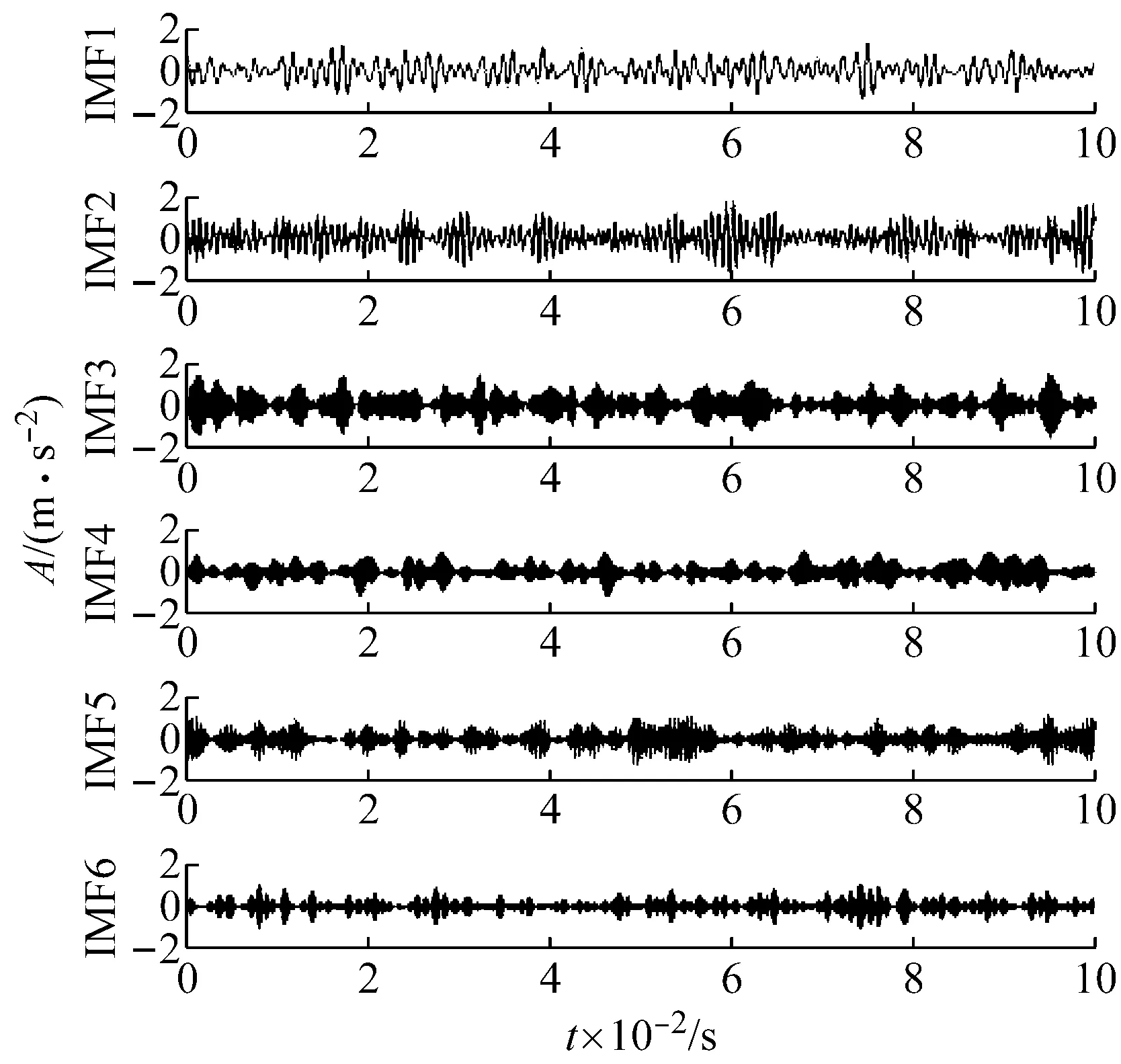
下面采用本文所述的改進VMD方法對仿真信號進行分解，層數k最大取15，當k取不同值時，計算原始信號與模態分量的能量差，能量差曲線如圖4(a)所示，從圖中可以看出當層數k為6時，能量差最小。將k值設為6，進行VMD分解，分解結果如圖4(b)所示。

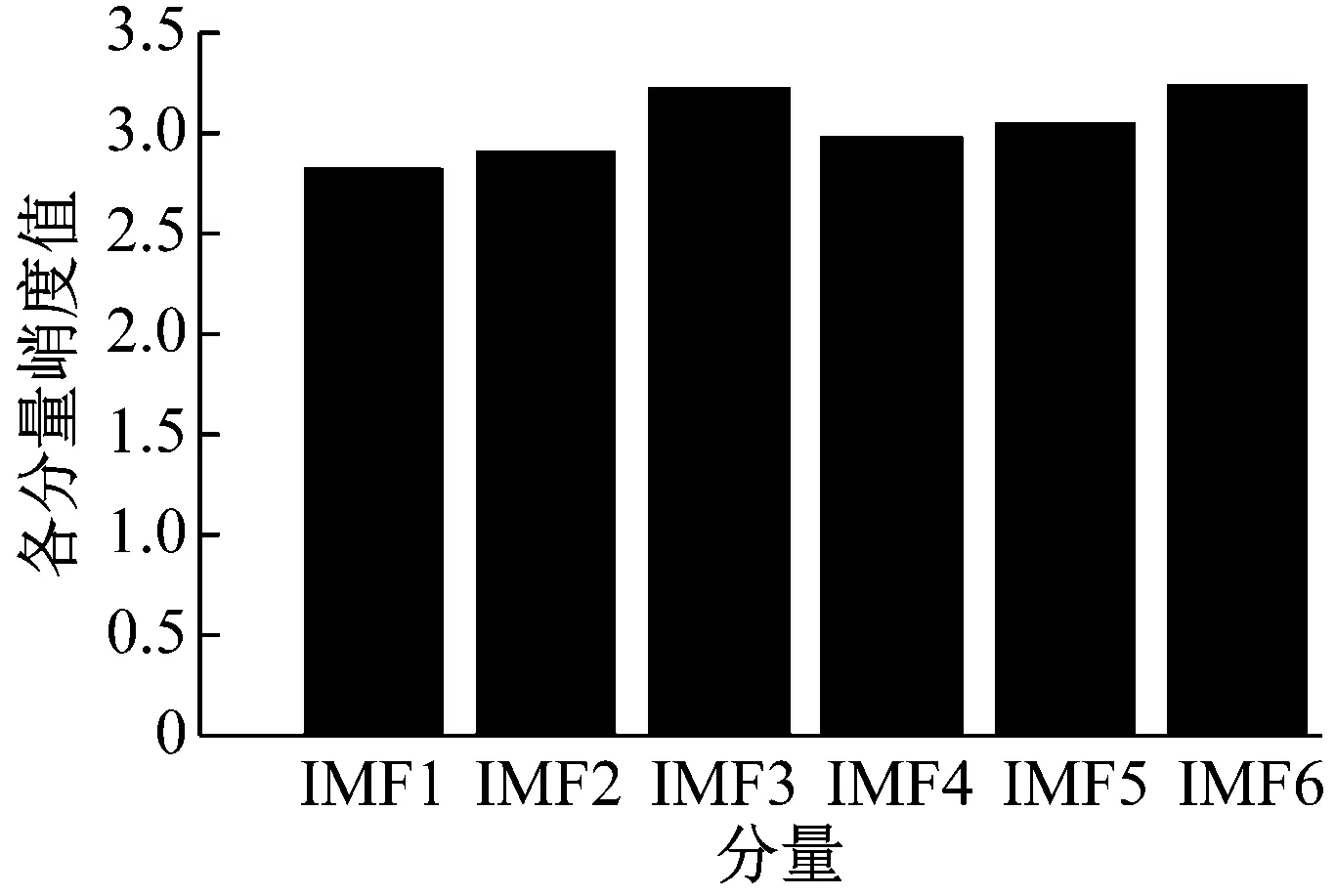
計算各分量的峭度值，如圖5(a)所示。根據峭度準則，選取IMF3,IMF5和IMF6三個峭度值較大的分量進行重構，重構信號如圖5(b)所示，重構信號的時域波形中出現了沖擊成分，但仍然存在噪聲干擾，采用本文所述的包絡導數能量算子解調方法，對重構信號進行解調，得到其能量譜如圖5(c)所示，在能量譜中顯示最大譜峰對應的頻率為179.7 Hz，其他357.4 Hz,537.1 Hz,716.8 Hz的峰值頻率與故障頻率的倍頻成分相對應，至此，本文方法成功地提取到故障特征頻率。

(a) 能量差曲線

(b) 分解結果

作為對比，采用Teager能量算子對重構信號進行解調分析，分析結果如圖6所示，盡管譜圖中可以觀察到故障特征頻率，但其他頻率成分干擾嚴重，提取效果不如圖4(c)包絡導數能量譜清晰。可見，包絡導數算子解調有一定的降噪功能，能更有效地提取故障特征信息。

3 實驗案例分析

實驗采用Spectra Quest公司的機械故障綜合模擬實驗臺，所采集的信號由DT9837型數據采集儀接入計算機進行分析保存。在實驗中分別對軸承的內圈、外圈、滾動體故障的加速度振動信號進行采集。如圖7所示，加速度傳感器安裝在靠近電機端軸承座的垂直、水平和軸向三個方向，圖8為軸承元件局部損傷示意圖。

3.1 外圈早期故障特征提取

外圈故障軸承采用ER-12K滾動軸承，節徑D=33.5 mm，滾動體直徑d=7.937 5 mm，接觸角α=0°，滾動體個數Z=8。實驗設置的采樣頻率為24 000 Hz，數據點數為12 000個點，電機轉速為1 200 r/min，轉頻為20 Hz，軸承外圈的故障頻率fouter為60.9 Hz。

(a) 各分量峭度直方圖

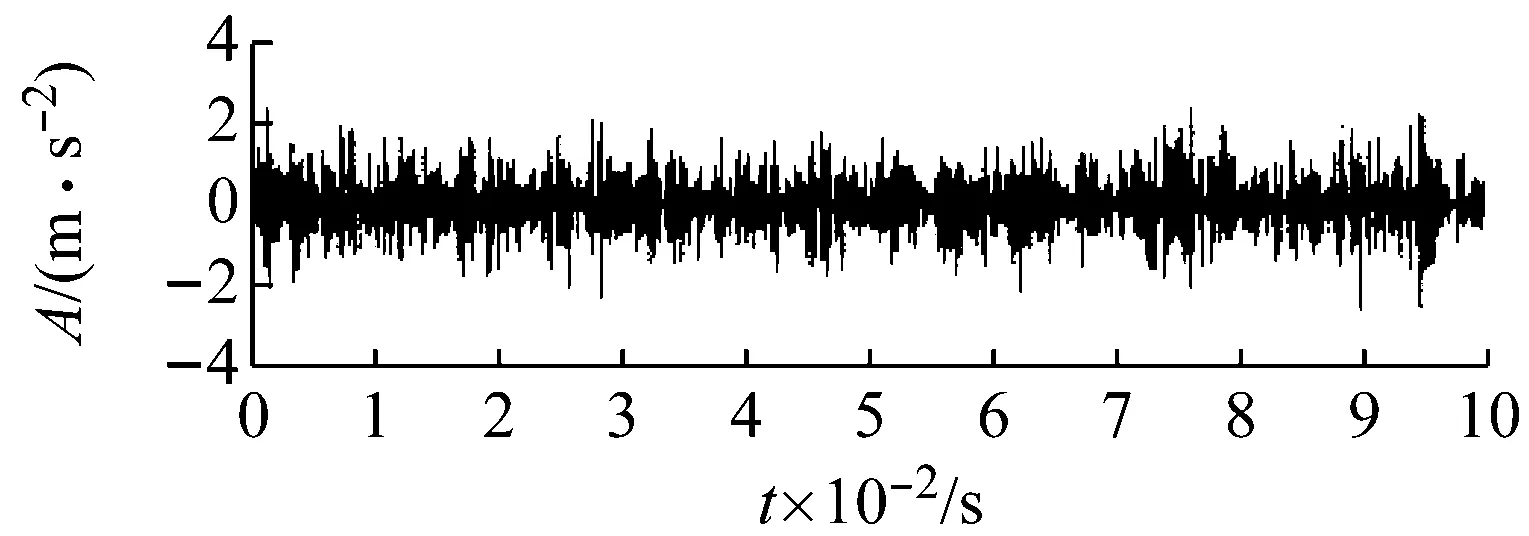
(b) 重構信號

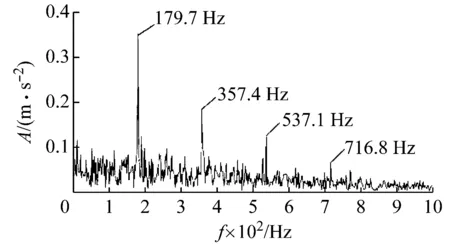
(c) 包絡導數能量譜

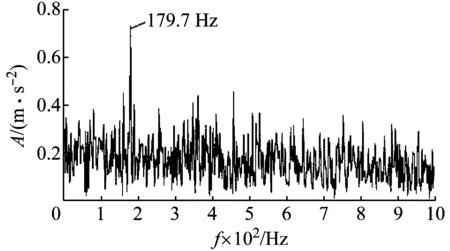
圖6 Teager能量譜

圖7 故障診斷實驗臺

圖8 滾動軸承元件損傷

圖9(a)為軸承外圈故障時所測得的時域波形，在時域信號中，沖擊成分明顯，噪聲成分較少。為了驗證本文方法在強噪聲環境下的有效性，在原始信號中加入-7 dB的高斯白噪聲，染噪后的時域信號如9(b)所示，時域信號中的沖擊成分已被噪聲淹沒。

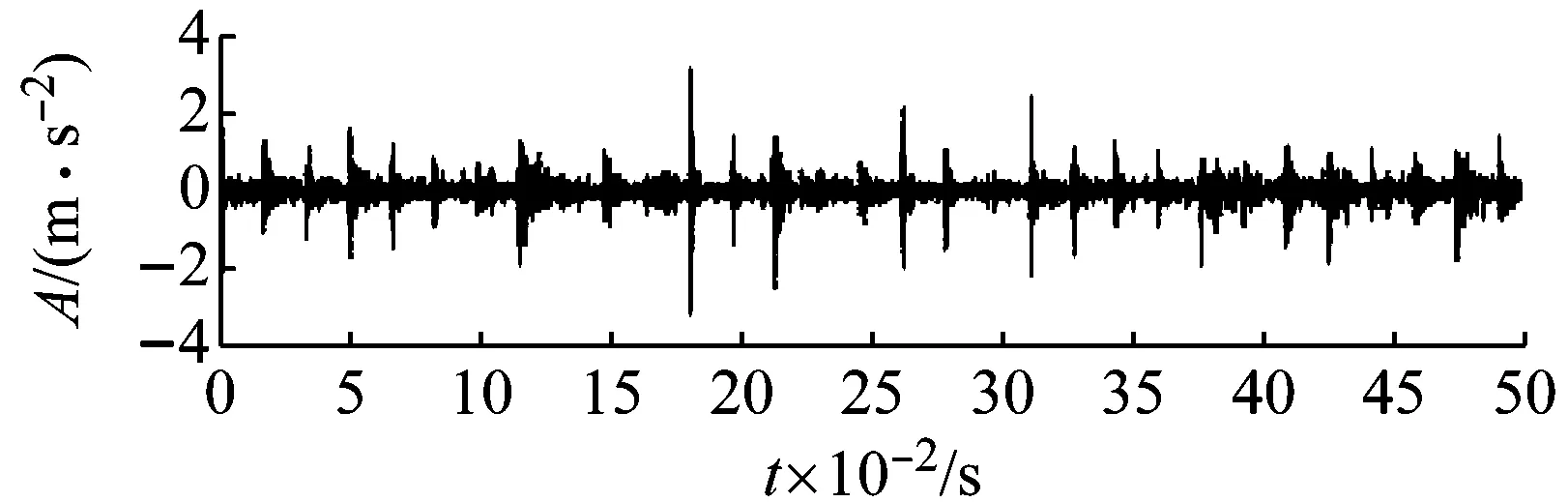
(a) 外圈故障信號

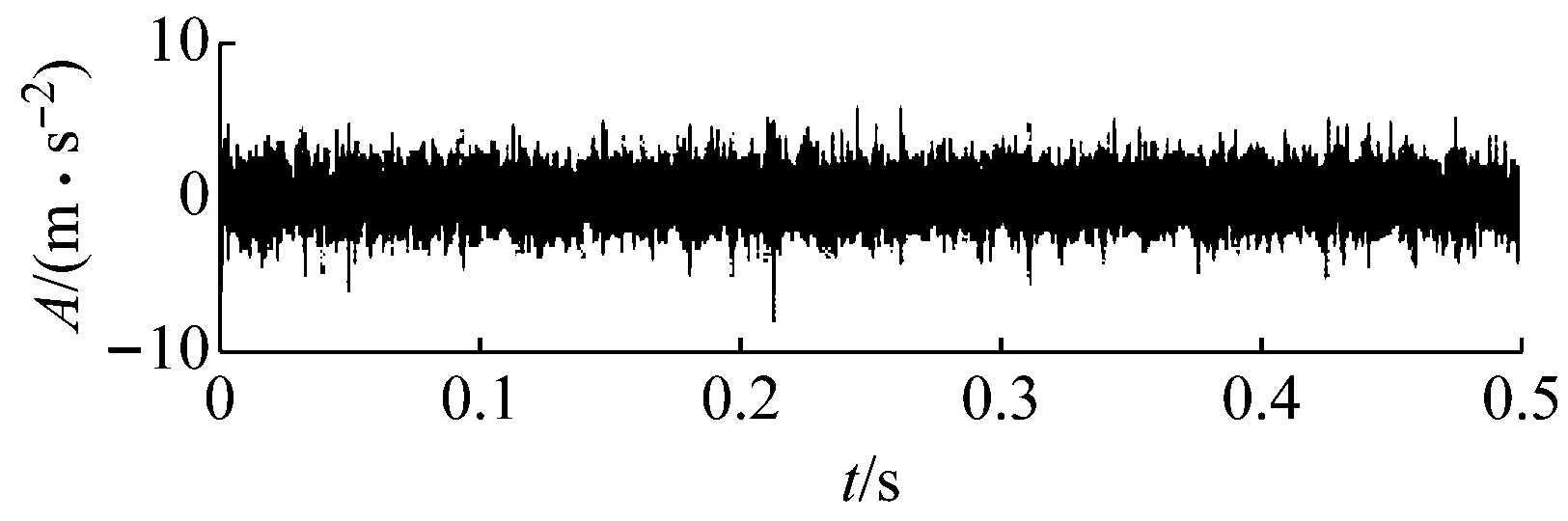
(b) 加噪聲后信號

采用本文所述的改進VMD方法對染噪信號進行處理，得到的能量差曲線如圖10(a)所示，從圖中可以看出當層數k值為6時，能量差最小。將k值設為6，進行VMD分解，分解結果如圖10(b)所示。

計算各分量的峭度值如圖11(a)所示，依據峭度準則，選取峭度值較大的IMF1和IMF6兩個分量進行重構，重構信號如圖11(b)所示，與染噪信號相比噪聲干擾明顯減少，但沖擊特征依然不明顯。對重構信號進行包絡導數能量算子解調，得到其能量譜如圖11(c)所示，從能量譜中能夠清晰地看到軸承外圈故障頻率62 Hz及其2,3,4等倍頻成分。至此，本文方法成功地提取到外圈故障特征頻率，實現了對軸承外圈早期故障的精確診斷。

作為對比，圖12為采用Teager能量算子對重構信號進行解調得到的能量譜，雖然在譜圖中能觀察到外圈故障特征頻率及其2倍頻成分，但是譜圖中含有較多的干擾成分，解調效果不如圖11(c)中清晰。

3.2 內圈早期故障特征提取

內圈故障軸承采用ER-16K滾動軸承，節徑D=38.5 mm，滾動體直徑d=7.937 5 mm，接觸角α=0°，

(a) 能量差曲線圖

(b) 分解結果

滾動體個數Z=9。內圈信號的采樣頻率為24 000 Hz，數據點數為12 000個點，電機轉速為1 380 r/min，轉頻為23 Hz，內圈的故障特征頻率finner為124.9 Hz。圖13為內圈故障時所測得的振動信號，由于噪聲干擾嚴重，時域信號中的故障沖擊成分被淹沒。

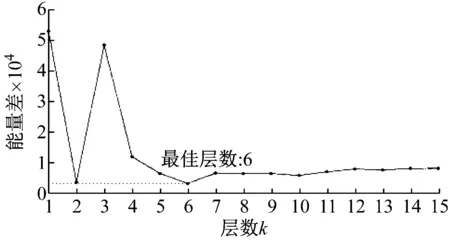
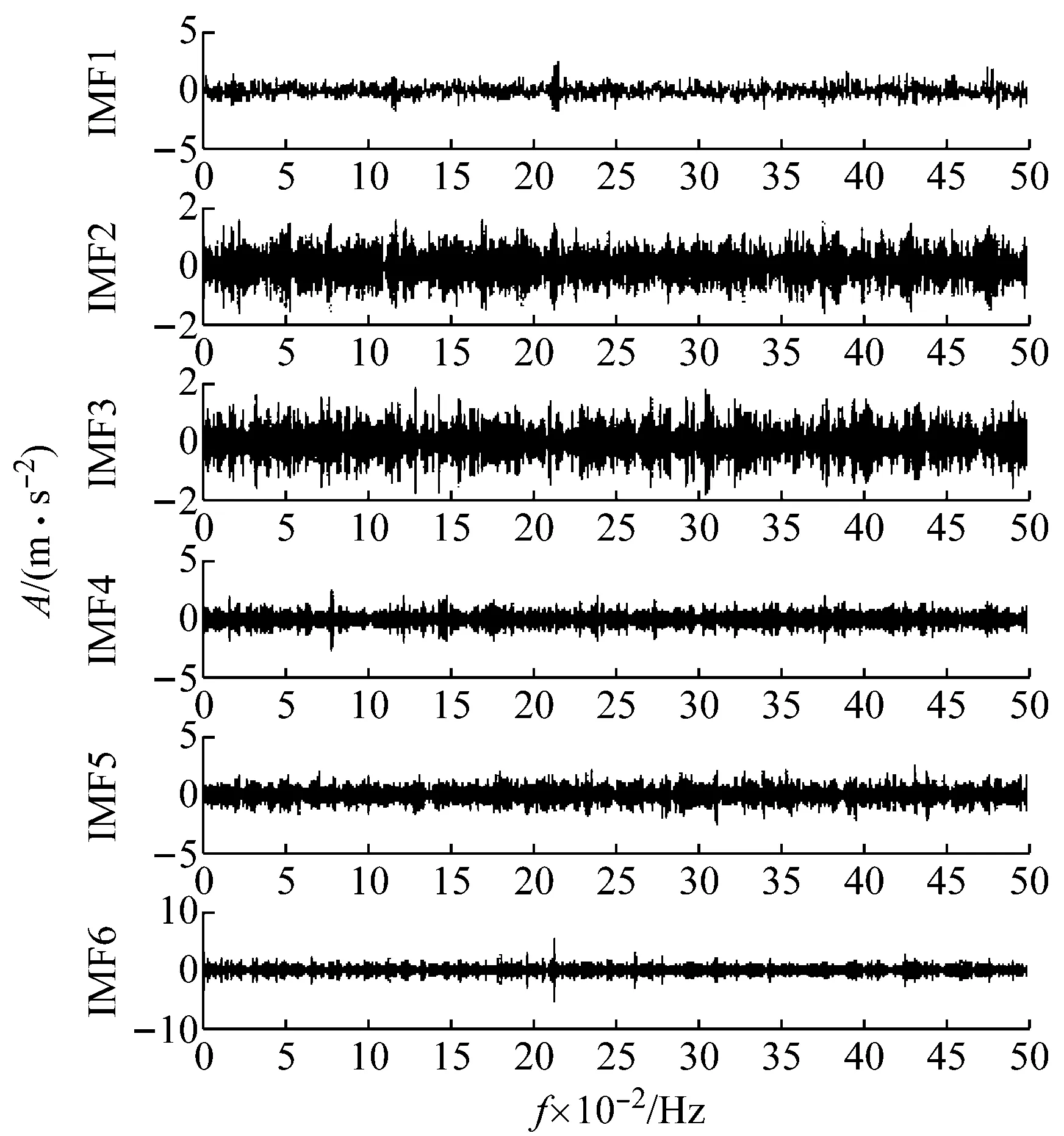
根據圖14可知最佳分解層數為6，將k設為6，對內圈故障振動信號進行VMD分解。再根據峭度準則，選取峭度值較大的IMF1,IMF5,IMF6三個分量進行重構，重構信號如圖15所示。雖然重構信號中仍然存在部分噪聲，但可以看到比較明顯的沖擊成分。

應用包絡導數能量算子對重構信號進行解調分析，得到能量譜如圖16所示，從能量譜中可以看到故障特征頻率124 Hz以及2倍頻、3倍頻成分，至此，本文方法成功地提取到內圈故障特征頻率，實現了對軸承內圈早期故障的精確診斷。作為對比，應用Teager能量算子對重構信號進行解調處理，結果如圖17所示，譜圖中其他頻率成分干擾嚴重，僅能觀察到一倍故障特征頻率，解調能力明顯不如導數包絡能量算子。

3.3 滾動體早期故障特征提取

滾動體故障軸承采用ER-12K軸承，采樣頻率為24 000 Hz，數據點數為12 000個，電機轉速為3 000r/min，轉頻為50 Hz，滾動體的故障特征頻率fball為99.6 Hz。滾動體故障時所測得振動信號如圖18所示，故障沖擊成分被噪聲淹沒，因此僅根據時域信號很難進行診斷。

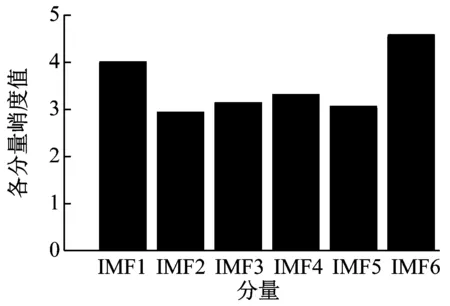
(a) 各分量峭度直方圖

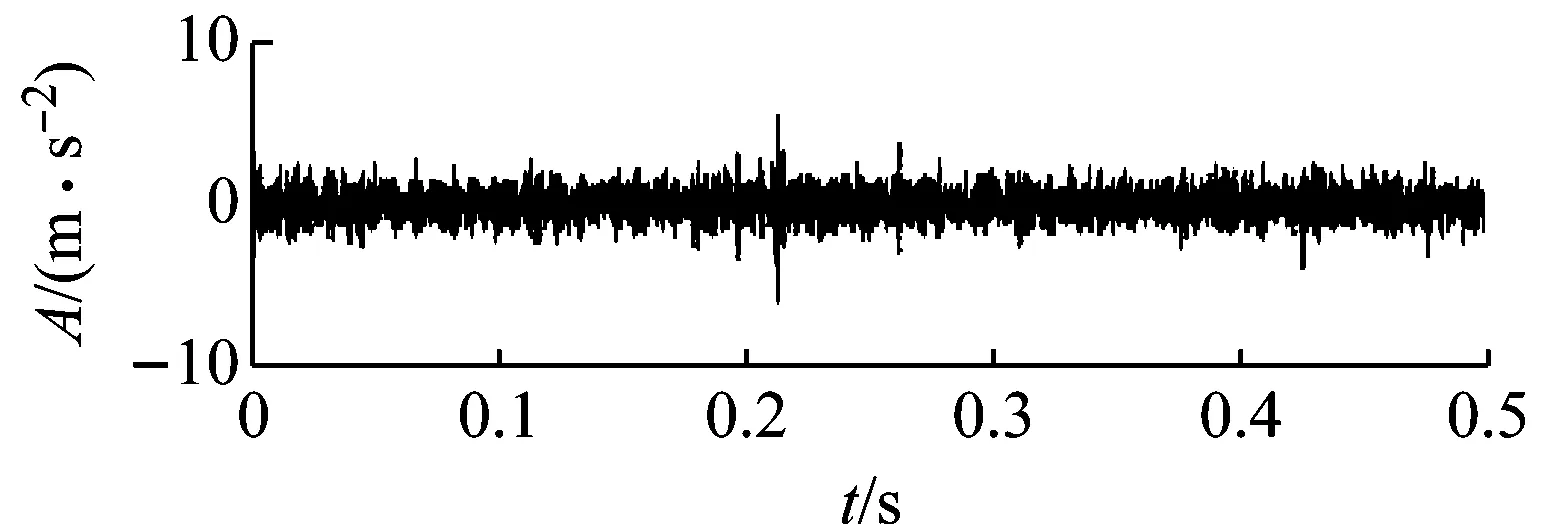
(b) 重構信號

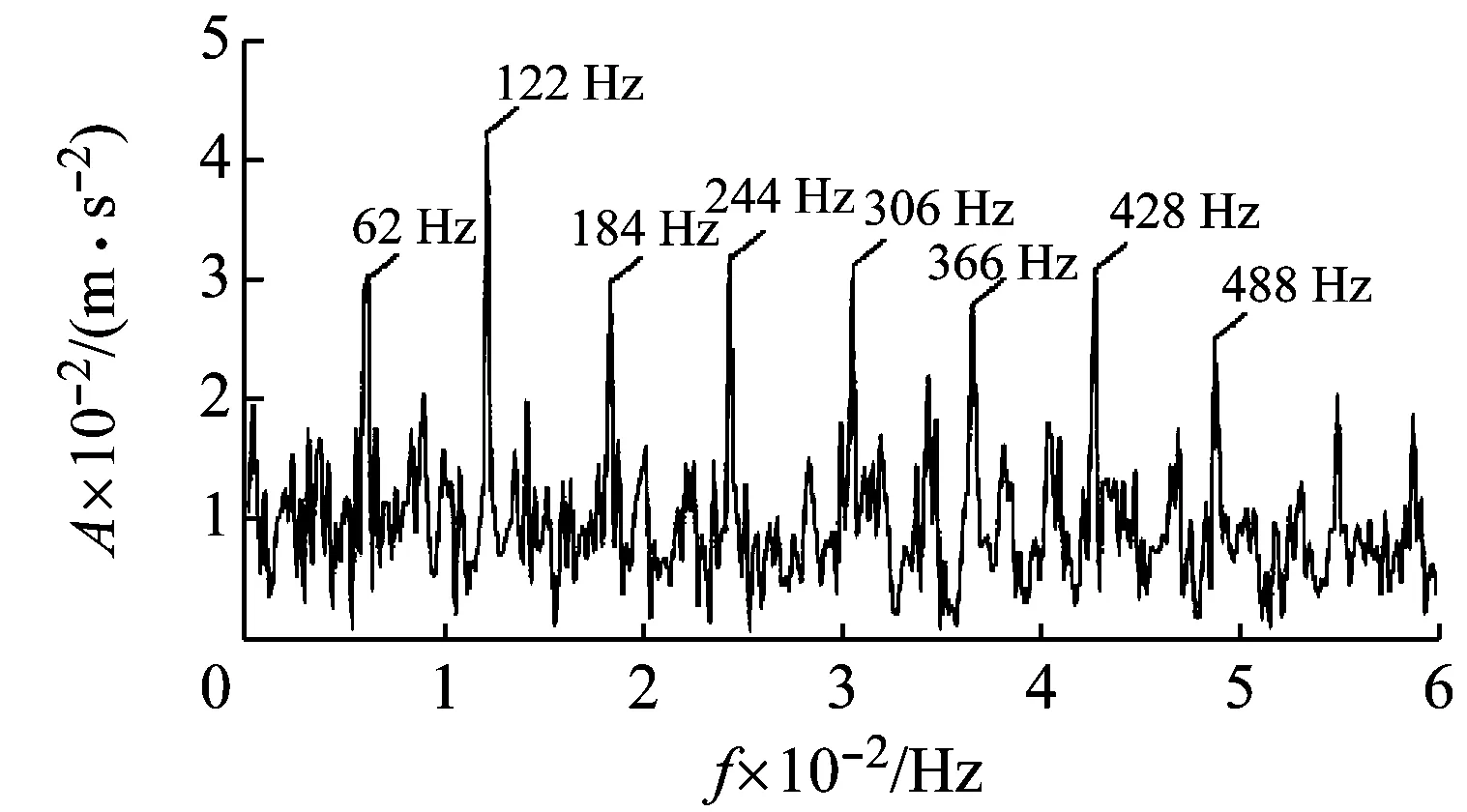
(c) 包絡導數能量譜

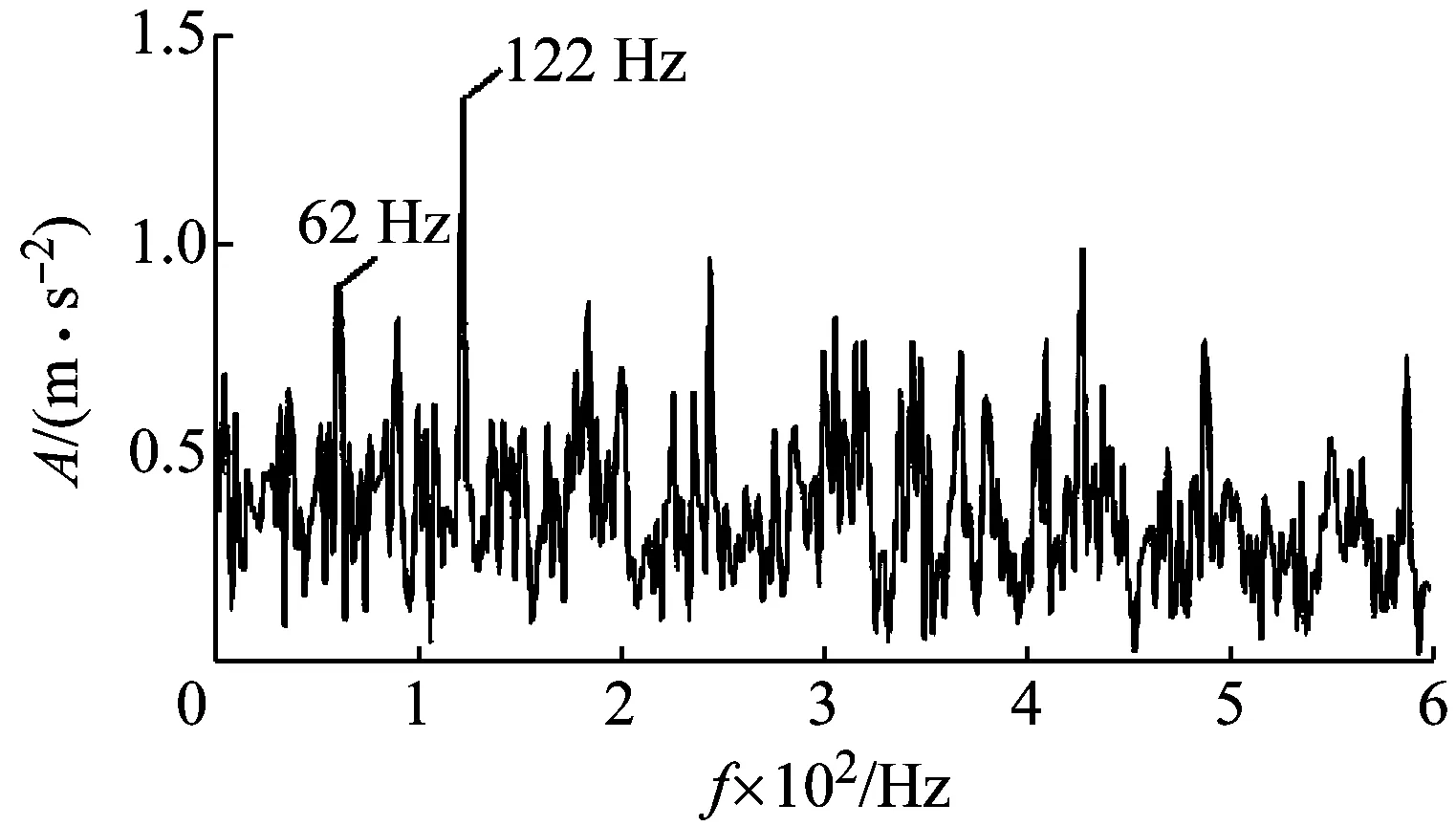
圖12 Teager能量譜

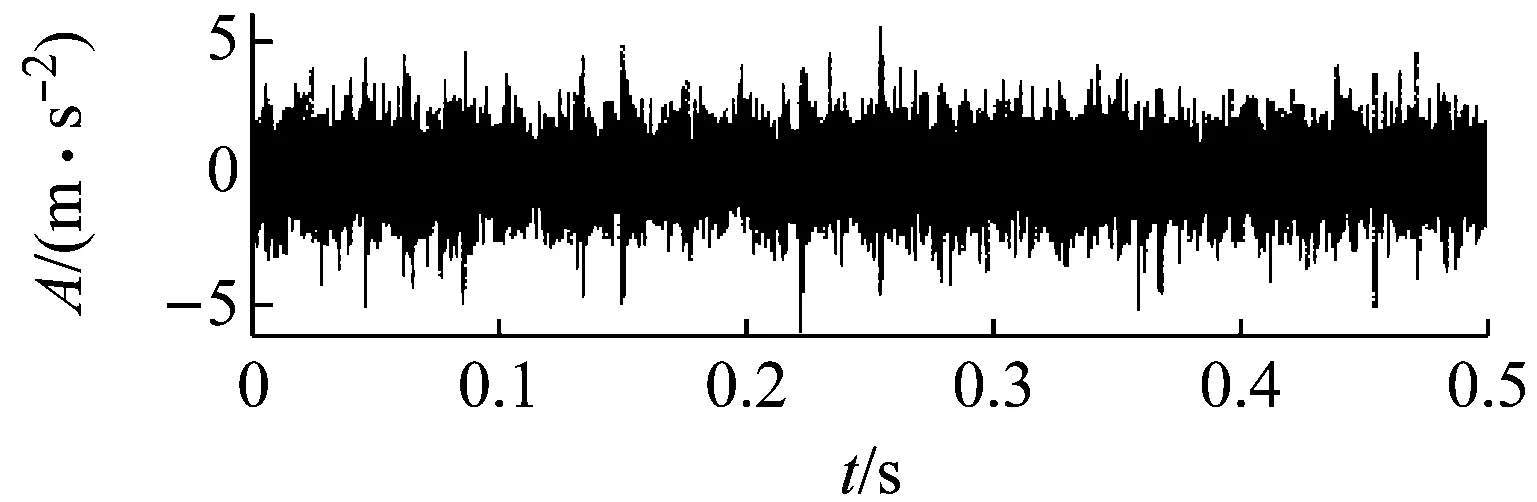
圖13 內圈故障時域信號

根據圖19可知最佳分解層數為6，將分解層數k設置為6，對滾動體故障振動信號進行VMD分解；然后依據峭度準則，選取峭度值較大的IMF4和IMF5兩個分量進行信號重構，重構信號如圖20所示。

圖14 能量差曲線圖

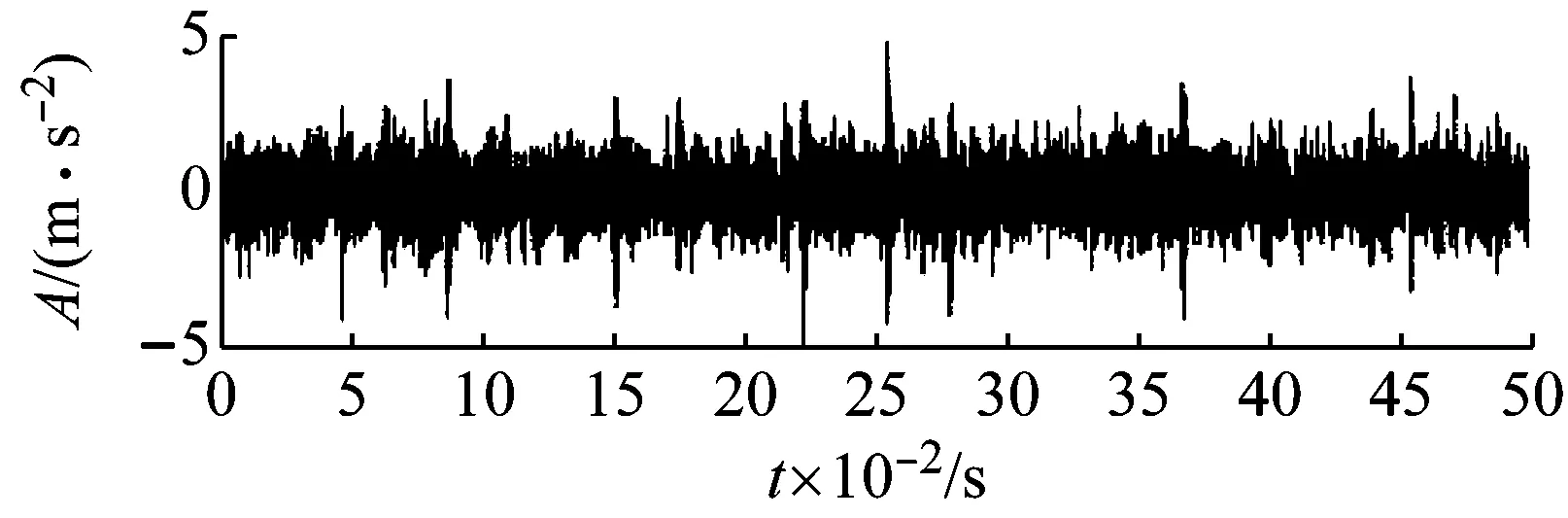
圖15 重構信號

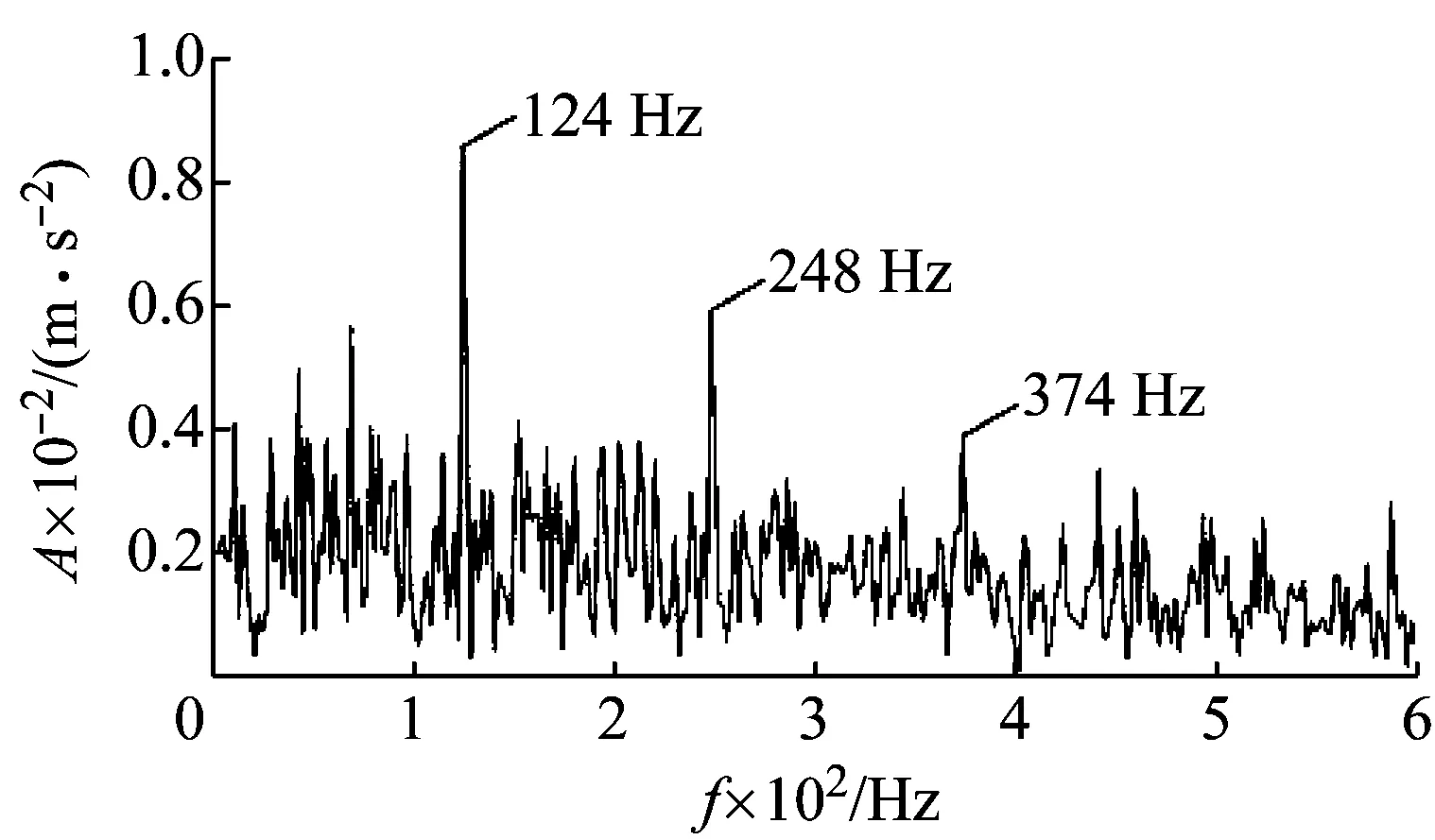
圖16 包絡導數能量譜

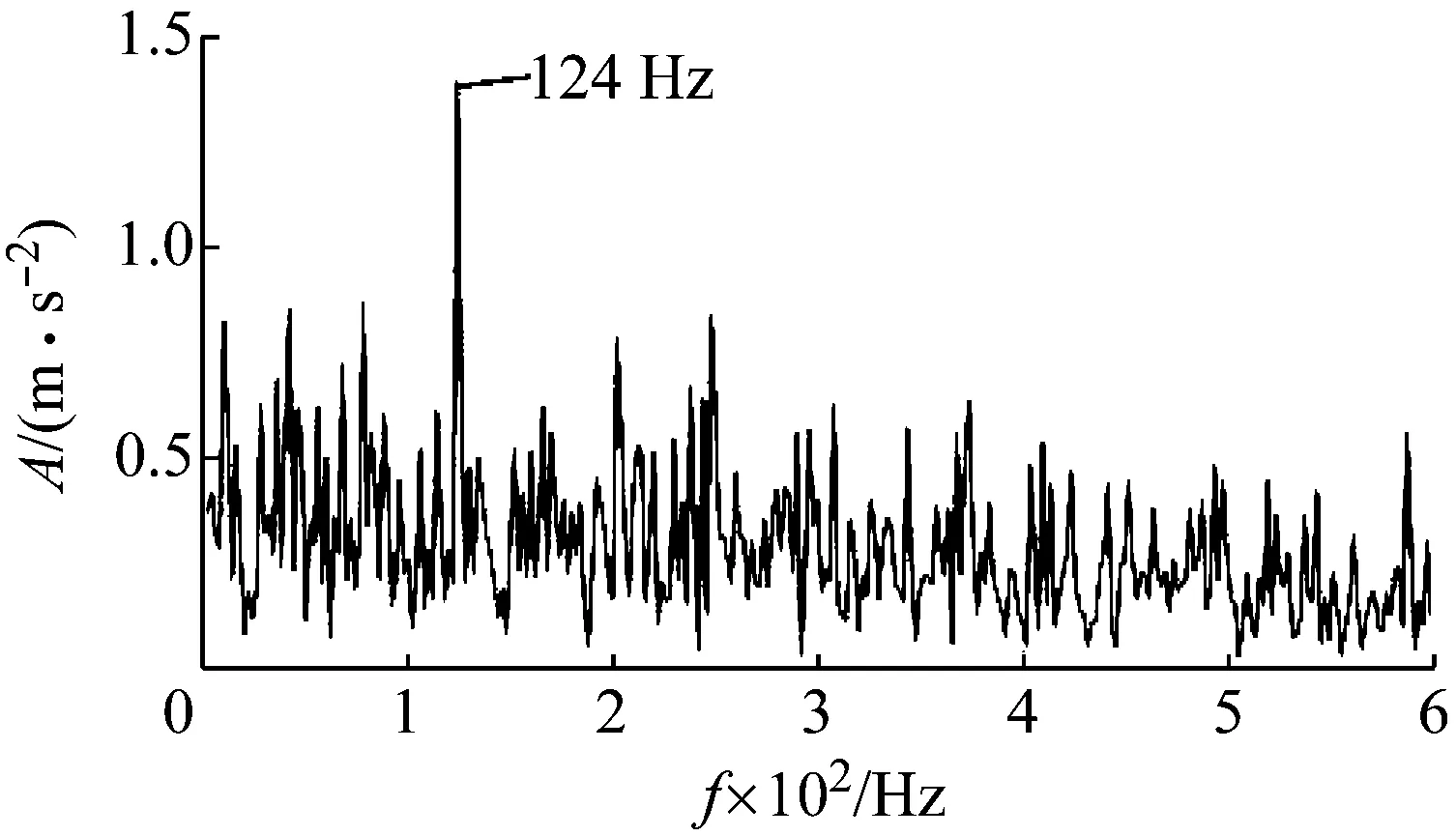
圖17 Teager能量譜

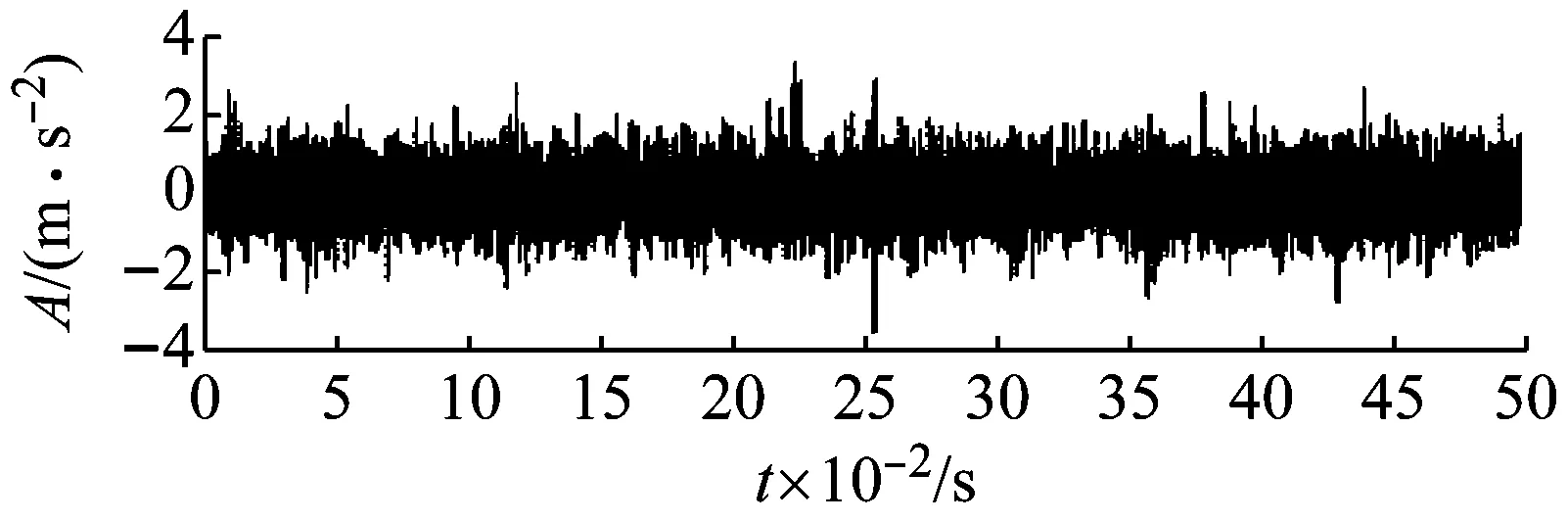
圖18 滾動體故障時域信號

采用包絡導數能量算子對重構信號進行包絡解調，得到其能量譜如圖21所示，從譜圖中可以觀察到滾動體故障特征頻率98 Hz及其倍頻成分。至此，本文方法成功地提取到滾動體故障特征頻率，實現了對軸承滾動體早期故障的精確診斷。圖22為對重構信號采用Teager能量算子解調后得到的能量譜，與圖21對比可知，圖21中包絡導數能量譜的特征要優于圖22中Teager能量譜。

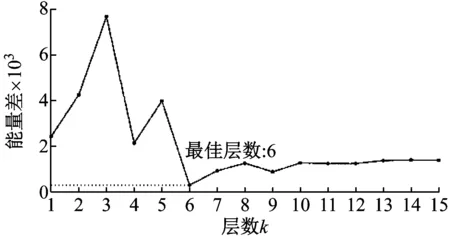
圖19 能量差曲線圖

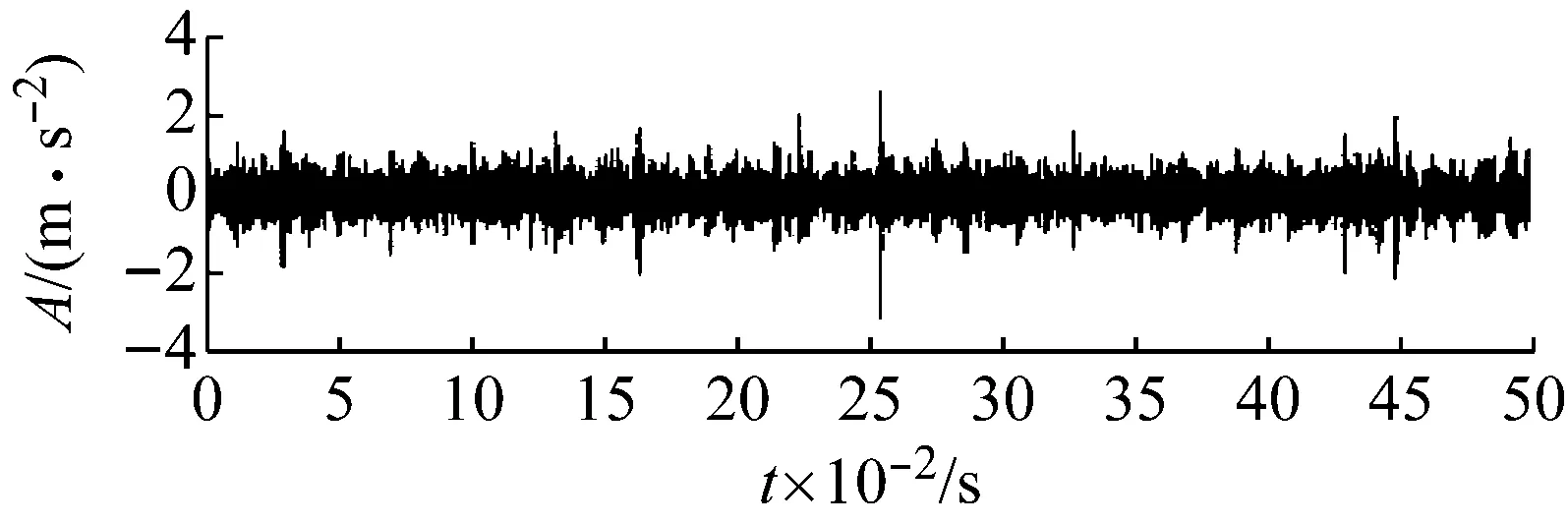
圖20 重構信號

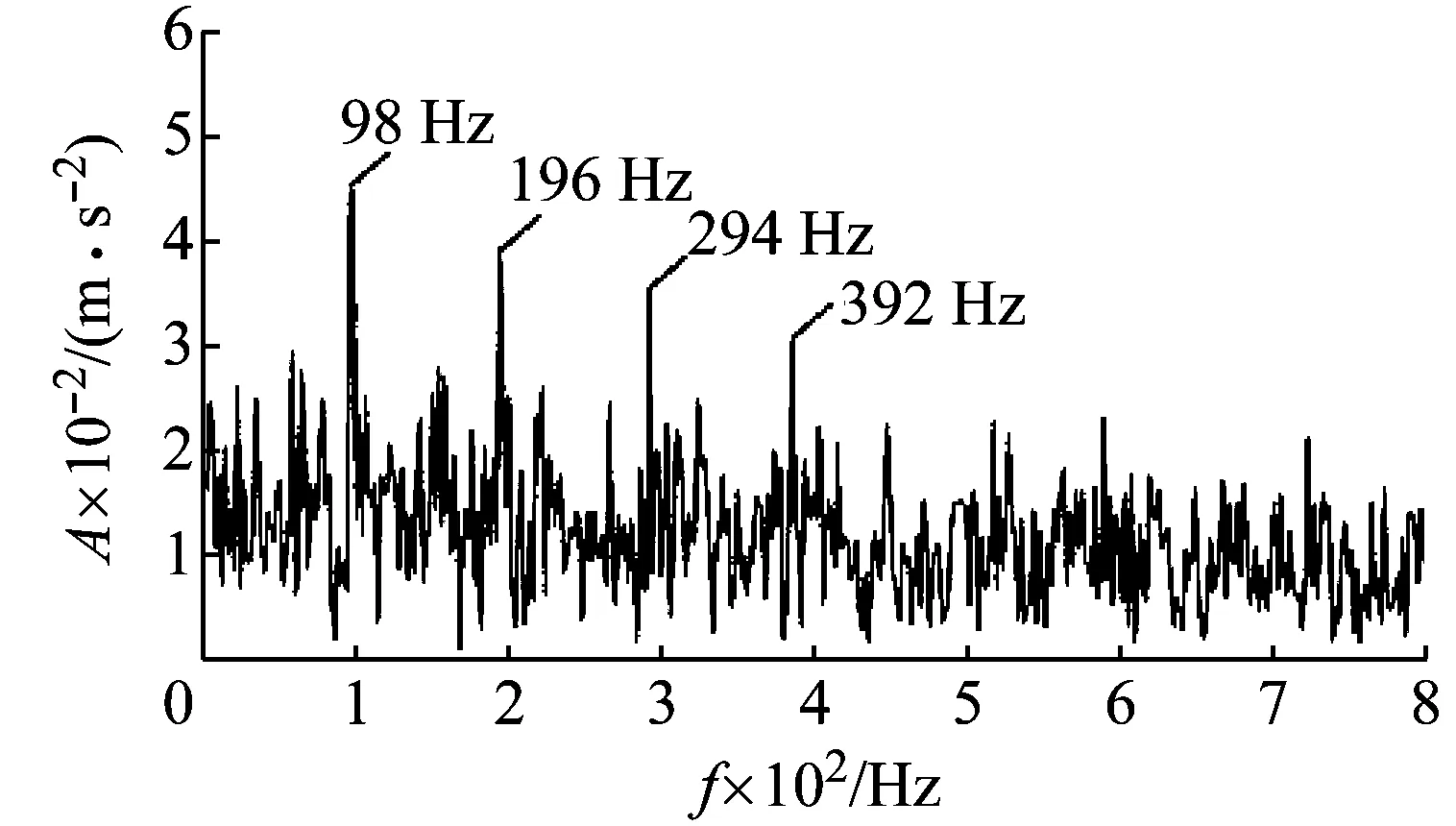
圖21 包絡導數能量譜

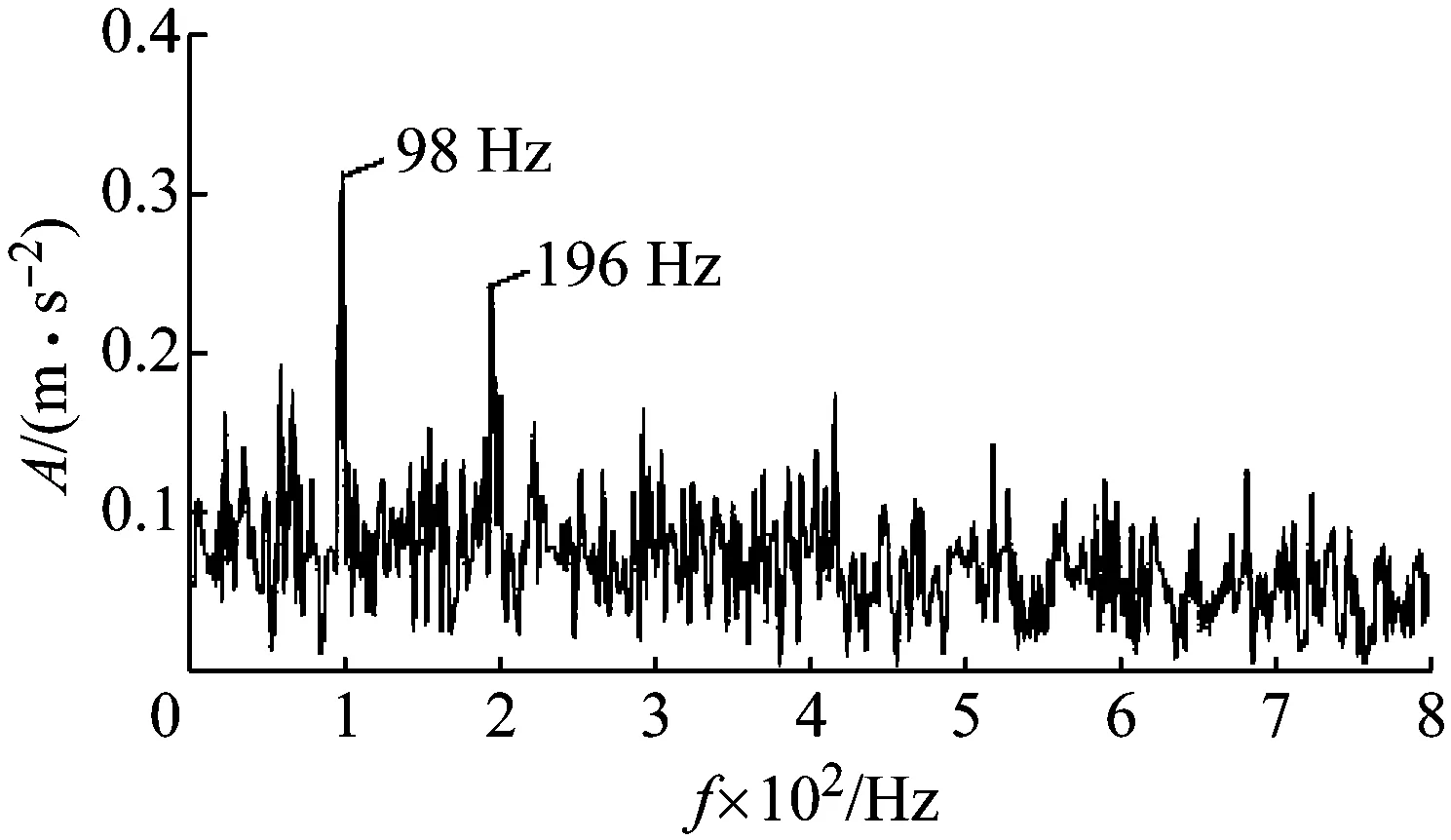
圖22 Teager能量譜

4 結 論

本文研究了基于改進VMD與包絡導數能量算子的早期故障診斷方法，通過對仿真信號和實驗數據分析結果可知，該方法非常有利于強噪聲背景下故障特征的提取，在軸承早期故障診斷中具有一定的優勢。

(1) 改進VMD以原始信號與本征模態分量的能量差作為評價參數，自適應地確定VMD的最佳分解層數k，有效地解決了VMD分解層數難以確定的問題；利用改進的VMD對故障信號進行分解，再依據峭度準則，選取敏感分量進行信號重構，有效地降低了噪聲干擾，保留了故障沖擊成分。

(2) 對含有較強噪聲的信號進行解調時，包絡導數能量算子與Teager能量算子相比，能夠有效地抑制噪聲，增強故障沖擊，更有利于故障特征的提取。

(3) 綜合兩種方法的優勢，將改進VMD與導數包絡能量算子相結合應用于軸承早期故障診斷中，保證了軸承早期故障特征提取的準確性與故障診斷的可靠性，為實際工程應用提供了一種切實可行的新方法。