齒輪箱故障非線性特征測度及狀態(tài)TWSVM辨識研究
曾 柯, 柏 林
(重慶大學 機械傳動國家重點實驗室,重慶 400044)
齒輪箱振動信號由于系統(tǒng)本身的復雜性,以及振動在傳輸過程中的衰減和耦合等,往往表現(xiàn)出非線性的特征。尤其是在發(fā)生故障時,故障源產(chǎn)生的激勵會使齒輪嚙合剛度產(chǎn)生相應的變化,這種故障引起的時變剛度使得齒輪振動的非線性和非平穩(wěn)性更加突出。另者,由于加工和安裝引起的誤差激勵以及非穩(wěn)態(tài)齒輪嚙合也會使得齒輪振動本身具有很強的非線性[1]。傳統(tǒng)線性和平穩(wěn)的特征提取技術,容易丟失重要的非線性狀態(tài)信息,不能很好地從復雜的非線性信號中提取真實反映其非線性振動本質(zhì)的有效狀態(tài)特征[2]。因此采用非線性特征測度方法對齒輪箱振動信號進行狀態(tài)分析,能夠更加準確地辨識出齒輪箱的狀態(tài)特征。
在傳統(tǒng)的模式識別方法中,SVM(Support Vector Machine)是一個二分類算法,對均衡或近似均衡分布的樣本,分類效果顯著[3]。但是對于一個多分類問題,SVM只能通過一對其余或二叉樹等多分類方法來實現(xiàn),但是這些多分類方法都不能解決樣本不均衡而導致分類精度降低的問題,SVM在處理該類問題時往往不盡人意[4]。所謂樣本不均衡一般是指用于訓練分類器的兩類樣本中,一類樣本的數(shù)量要遠大于另一類[5],樣本不均衡問題一般在多分類問題中會經(jīng)常出現(xiàn)。Jayadeva等[6]提出的TWSVM(Twin Support Vector Machine)可以通過參數(shù)的調(diào)整克服樣本不平衡問題[7]。具體來說TWSVM算法可以通過實施不同的懲罰因子以克服傳統(tǒng)SVM處理樣本非均衡問題的局限性[8],另外TWSVM其核心思想是構(gòu)造兩個非平行的超平面,并使正類樣本靠近正類超平面而負類樣本盡可能地遠離,使負類樣本靠近負類超平面而正類樣本盡可能地遠離,因此TWSVM的兩個非平行超平面比SVM的一個超平面對樣本不均衡問題的適應性更強。由于TWSVM訓練速度較快,能較好求解異或問題以及分類性能優(yōu)越等優(yōu)勢,它能夠有效提高故障辨識精度[9]。本文將首先采用多種非線性特征對齒輪箱振動信號的非線性性進行測度,并采用Fisher準則[10]對非線性特征集進行評價,最后采用TWSVM方法對齒輪故障狀態(tài)進行辨識。實驗結(jié)果表明,非線性特征測度方法能夠有效地提取齒輪箱振動信號狀態(tài)特征,并且采用TWSVM分類模型其分類準確率要高于SVM和BP神經(jīng)網(wǎng)絡的分類準確率,因此可以看出TWSVM算法分類性能優(yōu)勢明顯。
1 非線性特征的選取
基于非線性特征對于狀態(tài)的敏感性和魯棒性,本文選取分形維數(shù)和熵特征來提取齒輪箱振動信號的狀態(tài)特征。對時間序列提取非線性特征一般采取相空間重構(gòu)法,其原理是選擇合適的延時時間τ和嵌入維數(shù)m對原始時間序列X={x1,x2,…,xN}進行相空間重構(gòu),如式(1),以還原混沌時間序列中蘊藏的非線性特征。
(1)
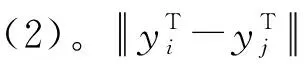
(2)
式中:H(u)為Heaviside函數(shù)
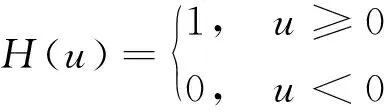
(3)
1.1 分形維數(shù)
分形維數(shù)是描述事物分形特性的一種有效方式,同時也是將事物分形特征進行量化的度量參數(shù)[11]。利用分形維數(shù)可以描述混沌時間序列吸引子的特征。分形維數(shù)的種類有很多,例如關聯(lián)維數(shù)、盒維數(shù)和Lyapunov指數(shù)等,關聯(lián)維數(shù)描述的是混沌時間序列具有某種確定的規(guī)律及程度,經(jīng)相空間重構(gòu)后的時間序列相互關聯(lián)的點對個數(shù)越多,就表明系統(tǒng)運動的規(guī)律性就越強。
原始時間序列經(jīng)相空間重構(gòu)后,可得關聯(lián)維數(shù)的表達式為
(4)
式中:C(r)為式(2)中的累計分布函數(shù);r為閾值。Dc由lnr-lnC(r)坐標圖中無標度區(qū)內(nèi)的點用最小二乘擬合所返回的斜率值得到。
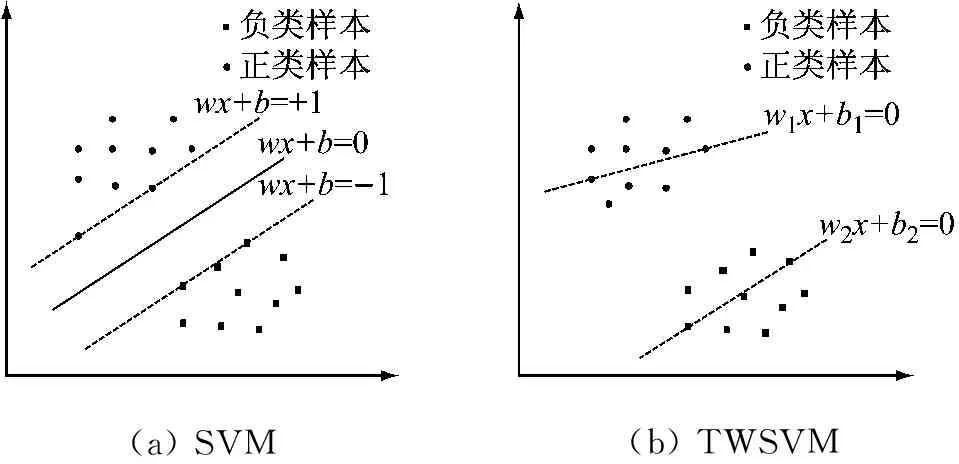
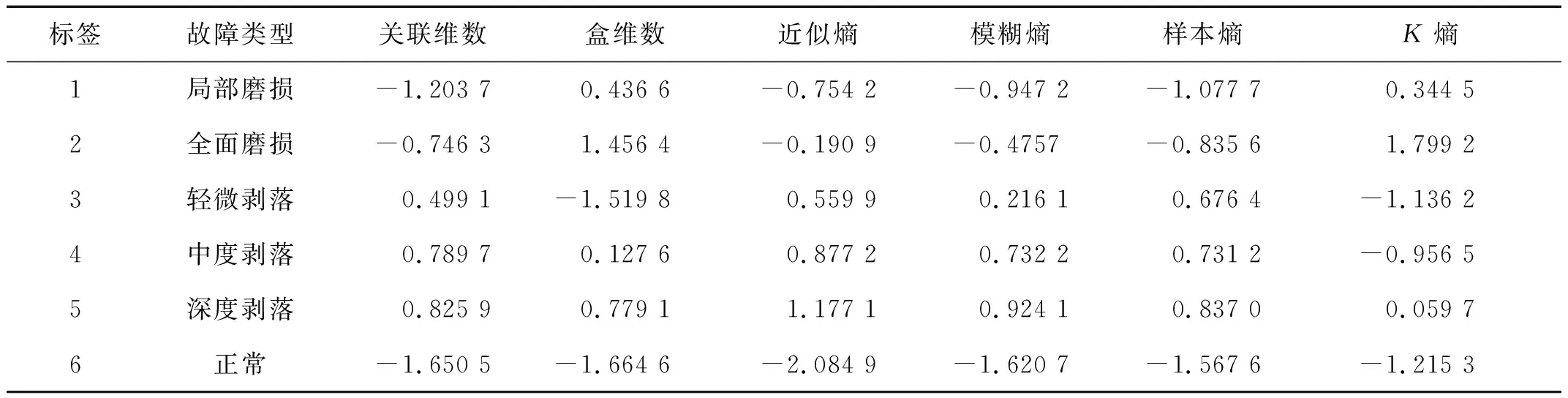
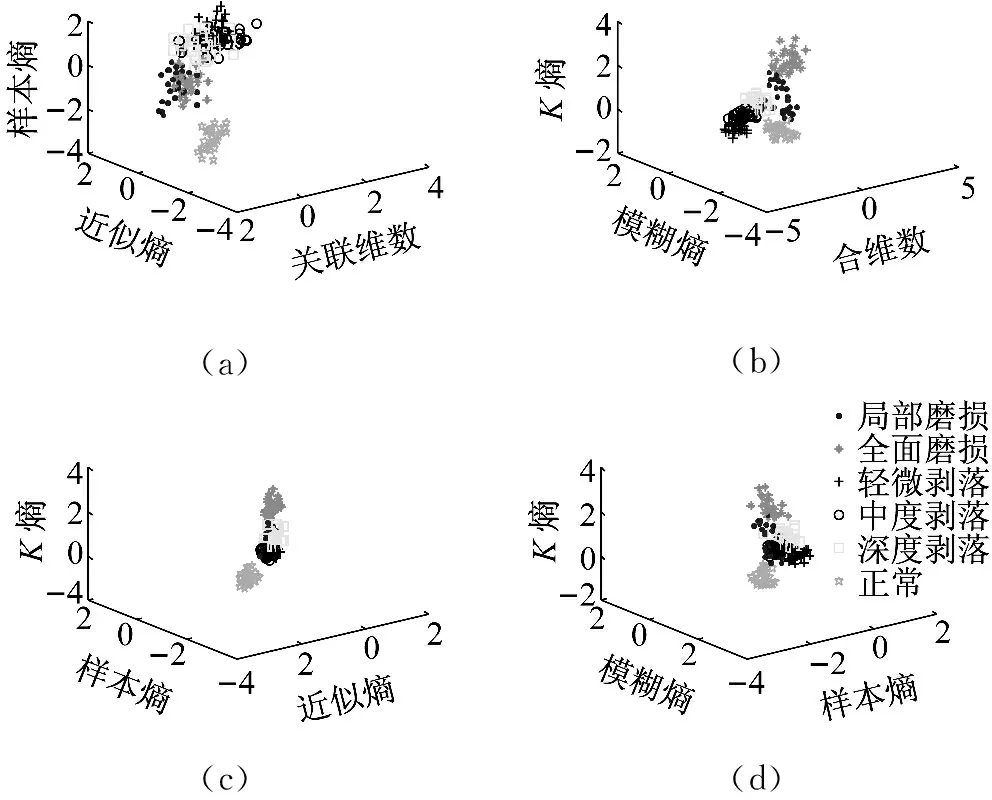
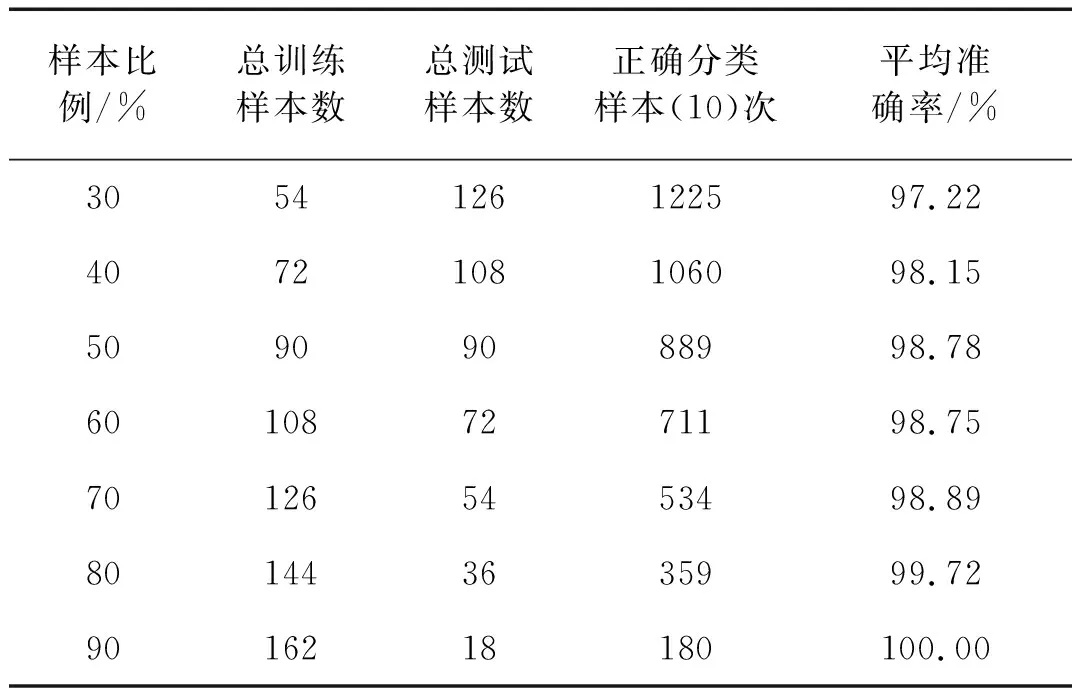
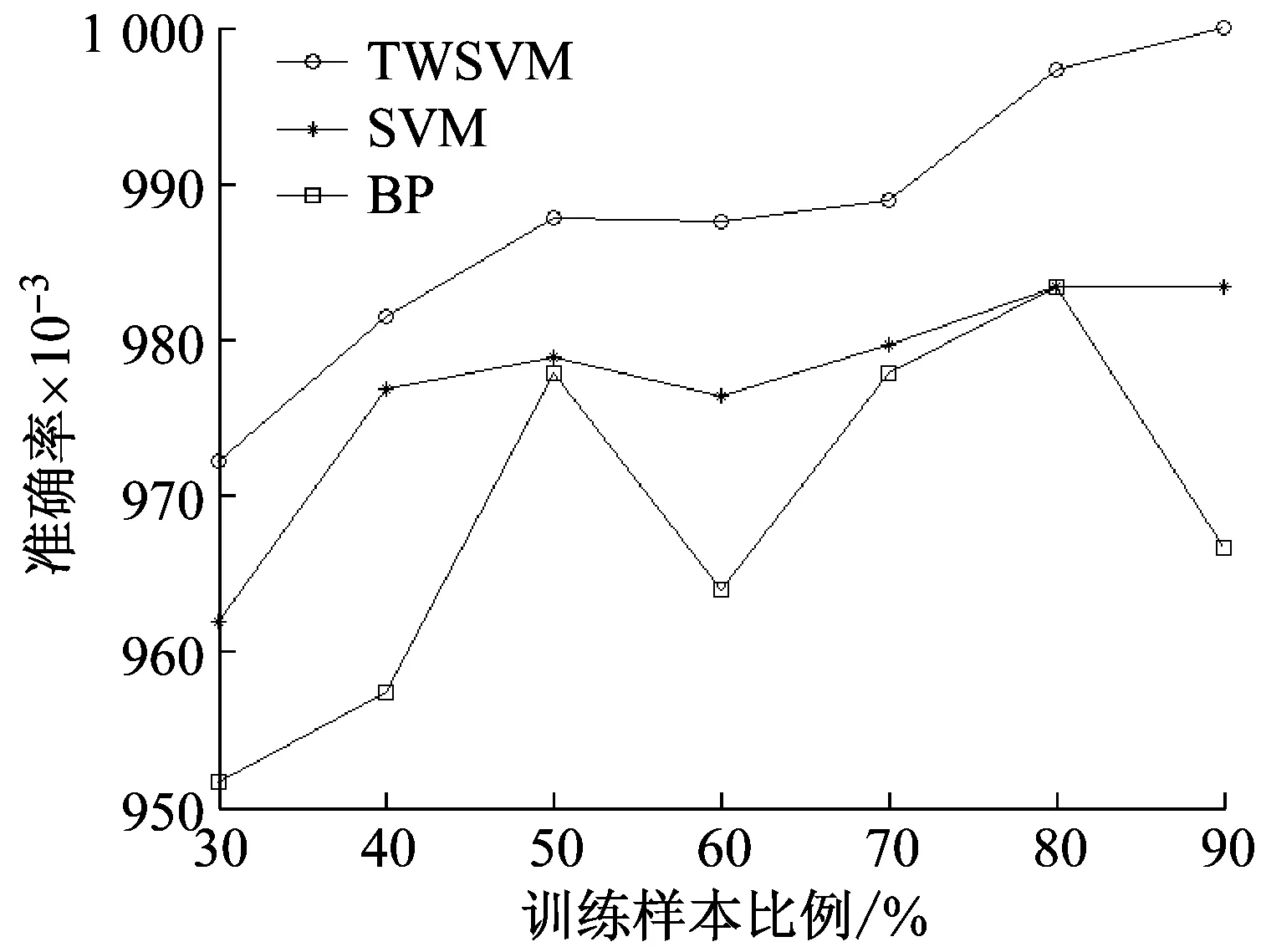
盒維數(shù)是將時間序列X劃分為間隔盡可能小的網(wǎng)格,設Δ為基準網(wǎng)格然后以Δ為基準逐步擴大網(wǎng)格的寬度使其為kΔ,k=1,2,…,M,M DB= (5) 近似熵用來描述某時間序列的復雜性,越復雜的時間序列對應的近似熵值越大[12],其算法也是定義在相空間重構(gòu)理論基礎之上: (6) (7) 步驟4然后改變重構(gòu)維數(shù)為m+1,重復上述過程可得φm+1(r),就可以得到近似熵 ApEn(m,r)=φm(r)-φm+1(r) (8) 由于重構(gòu)維數(shù)m和閾值r的選取對于近似熵ApEn的計算值有較大影響,因此m和r的選取顯得尤為重要,根據(jù)Pincus[13]在其論文中指出,當m=2,r=0.1-0.25SD(SD為時間序列標準差)時,近似熵值有較好的統(tǒng)計特性。 樣本熵分析方法只需要較短數(shù)據(jù)就可得出穩(wěn)健的估計值,是一種具有較好抗噪、抗干擾能力的非線性分析方法[14],其算法的步驟1和步驟2與近似熵算法的步驟1和步驟2,完全一樣,在完成步驟1和步驟2后,樣本熵計算步驟3如下 步驟3定義C(m)(r)為 (9) 步驟4增加維數(shù)到m+1,重復步驟2和步驟3可得 (10) (11) 步驟5定義樣本熵為 (12) (13) 然后增加重構(gòu)維數(shù)為m+1,重復上述計算過程,可得Φm+1(n,r),由此可得模糊熵FuzzyEn(m,n,r),即 lnφm+1(n,r)) (14) Kolmogorov熵值是非線性特性的度量量之一[16],是描述非線性系統(tǒng)產(chǎn)生信息量多少和快慢程度的物理量[17],其算法也是先對原始時間序列進行相空間重構(gòu)得到累計分布函數(shù)Cm(r),無標度區(qū)內(nèi)系統(tǒng)的Kolmogorov熵為 (15) 從定性的角度分析很難確定所提取特征樣本的質(zhì)量高低,為了能夠定量地分析特征樣本質(zhì)量,這里采用Fisher準則方法對所提取的非線性特征進行評價。其中Fisher算法基本思路是針對整個樣本集中第i個特征定義Fisher得分Fr為 (16) TWSVM比較于傳統(tǒng)的SVM所建立的一個超平面,TWSVM構(gòu)建了兩個非平行的超平面,并使正類樣本靠近正類超平面而負類樣本盡可能地遠離,使負類樣本靠近負類超平面而正類樣本盡可能遠離,如圖1所示。TWSVM將SVM的一個計算量大而復雜的二次規(guī)劃問題轉(zhuǎn)換為2個小規(guī)模的二次規(guī)劃問題,減小了計算復雜性。由于使用非平行的分類超平面,TWSVM在解決兩類樣本成交叉分布的分類問題時,具有更強的泛化能力[18]。 (a) SVM(b) TWSVM 圖1 SVM和TWSVM分類模型示意圖 Fig.1 Classification model diagram of SVM and TWSVM 當樣本是線性可分時,用線性的分類器就能夠?qū)︻A測樣本進行分類,并能夠保證其精度,并且計算量相對較小。當樣本是線性不可分時,用線性的方法來訓練分類器要么求不出解,要么得出的分類器測試精度很低。為解決線性不可分的問題,需要利用核函數(shù)將輸入樣本映射到高維特征空間,因為在高維特征空間中原來線性不可分的問題就變?yōu)榫€性可分。 非線性TWSVM的算法原理如下: 假設矩陣A代表第1類樣本集,矩陣B代表第2類樣本集,其中A∈Rm1×n,B∈Rm2×n。m1代表第1類樣本數(shù),m2代表第2類樣本數(shù),n代表特征向量維數(shù)。現(xiàn)在引入Mercer核函數(shù),K(xi,xj)=φ(xi)Tφ(xi)。那么非線性的TWSVM的2個二次規(guī)劃問題可以表示為TWSVM1和TWSVM2,即 TWSVM1 s.t. -(K(B,CT)u(1)+e2b(1))+ζ≥e2 ζ≥0 (17) TWSVM2 s.t. (K(A,CT)u(2)+e1b(2))+η≥e1 η≥0 (18) 針對TWSVM1和TWSVM2二次規(guī)劃問題,采用拉格朗日法求解,可得TWSVM1和TWSVM2的對偶問題分別為式(19)和式(21),具體推導過程可參考。 TWSVM1 s.t. 0≤α≤c1 (19) 式中:向量α=(α1,α2,…,αm2)T,G=[K(B,CT)e2];H=[K(A,CT)e1],其余變量之前已定義。 從TWSVM1的對偶問題的推導中可以得出 (20) TWSVM2 s.t. 0≤γ≤c2 (21) 式中:γ=(γ1,γ2,…,γm1)T;P=[K(A,CT)e1];Q=[K(B,CT)e2]。 從TWSVM2的對偶問題的推導中可以得出 (22) 只要求得了u(1),u(2),b(1),b(2),那么就可以求出分類所需要的兩個超平面 K(X,CT)u(1)+b(1)=0 K(X,CT)u(2)+b(2)=0 (23) 最終判別公式為 (24) 為了研究齒輪箱振動信號在非線性測度下的TWSVM辨識性能。本文選取由布魯塞爾自由大學提供的不同狀態(tài)類別的齒輪箱振動信號。其一共有5種故障類型和1種正常狀態(tài),共6種標簽類型,分別為局部磨損,全面磨損,輕微剝落,中度剝落,深度剝落和正常。分別讀取這6種標簽下的振動信號,得到其時域波形,并對時域信號進行FFT變換得到其對應的頻譜,如圖2所示。 圖2(a)中各小圖分別對應標簽為局部磨損,全面磨損,輕微剝落,中度剝落,深度剝落和正常的時域波形,圖2(b)中各小圖分別為局部磨損,全面磨損,輕微剝落,中度剝落,深度剝落和正常的幅值譜。時域波形僅從肉眼只能看出每種標簽下的振動信號都是包含著噪聲和調(diào)制的復雜信號,但是齒輪箱中的齒輪在實際運轉(zhuǎn)過程中它會受到驅(qū)動力,彈性力和阻尼等因素的影響,另外齒輪嚙合過程中摩擦力的變化、轉(zhuǎn)速不穩(wěn)定及其可能的突變性和輪齒的碰撞等會使得當齒輪出現(xiàn)故障時整個齒輪箱系統(tǒng)產(chǎn)生非線性振動,因此所測得的齒輪箱故障振動信號一般會表現(xiàn)出非線性和非平穩(wěn)的特征。傳統(tǒng)的時域和頻域分析法很難從非線性振動信號中提取有效的狀態(tài)特征,比如從圖2中不能很明顯地看到能夠反映狀態(tài)類別的特征信息。因此如果采用線性的方法來對信號提取特征,必然會丟失信號的非線性成分,那么采用非線性測度方法來對時域信號提取特征就顯得尤為重要。 針對數(shù)據(jù)樣本的6種標簽,每類標簽選取30個樣本,每個樣本截取1 024個點,一共構(gòu)成180個數(shù)據(jù)樣本,組成維數(shù)為1 024×180的數(shù)據(jù)樣本矩陣。 分別對180個數(shù)據(jù)樣本中的每個樣本提取特征,每個樣本共提取6個特征,要提取的特征分別為關聯(lián)維數(shù)、盒維數(shù)、近似熵、模糊熵、樣本熵和K熵。由此組成維數(shù)為6×180的特征矩陣并歸一化處理,根據(jù)整體樣本集中不同特征值隨類別標簽變化的統(tǒng)計規(guī)律及趨勢選擇了其中部分特征向量值得到如表1所示數(shù)據(jù)。從表1可以看出所選擇的6個特征算法所得到特征值對故障類別較為敏感,并且隨著故障程度的加深呈現(xiàn)出一致性的規(guī)律,如正常狀態(tài)即無故障振動信號的特征值最小(即負得相對最多),在同種故障類型下,局部磨損和全面磨損相比,局部磨損的特征值要小于全面磨損;輕微剝落,中度剝落和深度剝落相比,輕微剝落的特征值要小于中度剝落的特征值,中度剝落的特征值要小于深度剝落的特征值。總結(jié)起來就是故障程度越小其振動信號的混沌特性越不明顯因而特征值越小,而故障程度越大其振動信號的混沌特性也就越明顯因而特征值相對較大。為了能夠定量地對特征值進行評價,本文選用Fisher得分算法來對特征進行打分,對原特征矩陣進行歸一化處理后,將特征矩陣輸入到Fisher函數(shù)中,得到其結(jié)果如表2所示。 表1 部分特征向量參數(shù) 表2 Fisher算法打分結(jié)果 從表2中可以看出,K熵的得分最高,盒維數(shù)的得分相對較低,其他特征的得分處于這兩者之間,為了更為直觀地觀察特征樣本集在空間中的分布,將這6個特征中每3個特征一個組合,一共選取4個組合來分析特征的聚類程度,從圖3中可以看出各種狀態(tài)類別的特征值在空間中呈現(xiàn)出一定的聚集狀態(tài),呈塊狀或者云狀分布。但是深入觀察可以發(fā)現(xiàn)圖3(a)~圖3(d)中不同故障類別的特征值樣本之間任有一些重疊,那是因為針對不同狀態(tài)類別只選取了3個維度的特征值,在添加了剩余的特征維度之后,特征向量將被映射到更高維的空間中,其特聚類性將更加明顯。綜上所述,采用非線性特征方法能夠有效提取齒輪箱狀態(tài)特征。 (a)(b)(c)(d) 圖3 3個特征值維度下的特征聚類分析 Fig.3 Clustering analysis of features based on three characteristic value 在每類標簽30個樣本中選定訓練樣本和測試樣本的比例,為了比較不同訓練樣本的比例對TWSVM算法分類精度的影響,本文選擇訓練樣本的比例分別為30~90%,剩下的作為測試樣本集。 針對一共6類標簽類型以及所確定的訓練樣本和測試樣本的比例,隨機抽取樣本,以10折交叉檢驗的方法避免偶然性誤差。表3給出了TWSVM在不同的訓練和測試樣本比例情況下的識別性能。 從表3可以看出TWSVM的訓練準確率能夠達到97.22%以上,并且隨著訓練樣本比例的增加其準確率呈上升趨勢,當訓練樣本比例為90%時,其準確率達到100%,這足以說明基于非線性特征測度的TWSVM有很高的分類準確率。 表3TWSVM在不同訓練、測試樣本數(shù)情況下識別性能 Tab.3RecognitionperformanceofTWSVMbasedondifferenttrainingandtestsamples 樣本比例/%總訓練樣本數(shù)總測試樣本數(shù)正確分類樣本(10)次平均準確率/%3054126122597.224072108106098.1550909088998.78601087271198.75701265453498.89801443635999.729016218180100.00 為了體現(xiàn)TWSVM分類方法的優(yōu)勢,在同等條件下將TWSVM與SVM和BP神經(jīng)網(wǎng)絡進行對比,如圖4所示。從圖4中可以看出,TWSVM、SVM和BP神經(jīng)網(wǎng)絡3種算法的分類準確率都隨著訓練樣本的增加而整體呈上升趨勢,但是TWSVM算法隨著訓練樣本比例的增加其準確率呈現(xiàn)較為均衡的上升趨勢,而SVM和BP算法其準確率的波動性較大,特別是BP方法,當訓練樣本比例為60%和90%時其準確率有較大幅度的降低。 圖4 TWSVM,SVM和BP分類準確率對比 特別地,當訓練樣本比例從30%一直上升到90%時,TWSVM算法的平均準確率整體上一直都高于SVM和BP算法,因此從整體上可以看出TWSVM算法要優(yōu)于SVM和BP神經(jīng)網(wǎng)絡。另外值得注意的是本文不管是采用TWSVM還是SVM來分類,均采用的是偏二叉樹方法來實現(xiàn)多分類目標,而偏二叉樹方法必然會產(chǎn)生訓練樣本不均衡性問題,因此從試驗結(jié)果可以看出TWSVM比SVM具有更高的樣本不均衡適應性。 由于齒輪的振動一般是非線性的,因此對其振動信號提取特征需采用非線性特征測度的方法。本文選取了關聯(lián)維數(shù)、盒維數(shù)、近似熵、模糊熵,樣本熵和K熵,這6個非線性特征參數(shù)來對帶有局部磨損、全面磨損、輕微剝落、中度剝落、深度剝落和正常這6狀態(tài)類型的齒輪箱振動信號進行特征提取。并用Fisher得分算法對特征進行打分,另外用特征云圖的方法對特征的聚類性進行直觀地描述。另外為了體現(xiàn)出TWSVM算法的優(yōu)越性,將其與BP神經(jīng)網(wǎng)絡和SVM算法的分類精度進行對比,可以得出如下結(jié)論: (1)采用非線性特征測度方法對齒輪箱振動信號進行狀態(tài)類別分析,能夠更加準確地辨識出齒輪箱工作狀態(tài),有助于后期構(gòu)建準確的分類模型。 (2)采用TWSVM作為分類模型,以所提取的非線性特征集作為訓練和測試樣本集,得到在不同訓練樣本比例下的整體識別精度可以達到97.22%以上,訓練樣本比例越高準確率越高。在同等條件下TWSVM模型分類準確率整體上要高于BP神經(jīng)網(wǎng)絡和SVM,并且TWSVM具有更高的樣本不均衡適應性。
1.2 近似熵、樣本熵、模糊熵和K熵

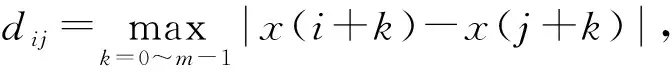
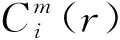
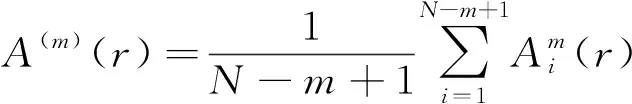
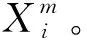
2 特征評價算法
3 非線性TWSVM原理
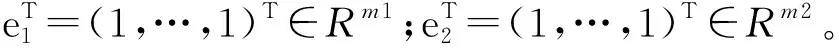
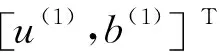
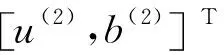
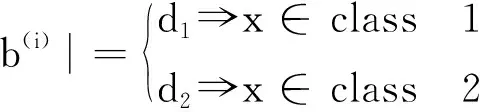
4 實驗研究

5 結(jié) 論

