基于車-橋隨機振動模型的簡支梁橋墩頂垂向動反力特征研究

朱志輝， 黃承志， 王力東， 時 瑾， 余志武， 蔡成標

(1. 中南大學 土木工程學院， 長沙 410075； 2. 中南大學 高速鐵路建造技術國家工程實驗室， 長沙 410075；3. 北京交通大學 土木建筑工程學院， 北京 100044； 4. 西南交通大學 牽引動力國家重點實驗室， 成都 610031)

隨著高速鐵路的快速發展以及城市規模的日益擴大，大量高架線路通過城市密集居民區、工業區等振動敏感點，高速列車帶來的環境振動問題日益嚴重[1]。列車在高架線路上運行時，動載作用通過梁體、支座傳遞至橋墩，相鄰橋墩墩頂垂向動反力以列陣點振源的方式引起環境振動，并進一步誘發附近地下結構以及周邊建筑物的二次振動及噪聲[2-3]。國內外的學者在開展高架軌道交通列車運行引起的環境振動問題時，通常采用兩種計算模型。一種是列車-橋梁-墩-樁-土-臨近建筑物整體耦合動力學模型，這種模型雖然從理論上更為接近實際，但由于自由度過于龐大，往往計算效率較低，制約了這種方法的廣泛應用；第二種模型采用兩步法開展研究[4]，首先確定墩頂動反力，然后把墩頂動反力施加在樁基-土體模型上計算環境振動，這種方法由于簡化了建模難度，提高了計算分析效率，但采用該方法最關鍵的問題是確定合理的墩頂動反力計算模型。

Cao等[5]采用半解析數值方法求解了列車通過連續梁時的墩頂反力，以此反力計算結果為輸入量分析了列車引起的大地振動特征；Wu等[6]采用半解析方法推導了一系列移動荷載作用下簡支梁橋墩頂反力；邊學成采用動力子結構法，研究了高速列車運動荷載作用下高架橋-群樁基礎-周圍場地土振動問題；蔣通等[7]采用簡化的車橋系統模型計算了墩頂動反力。以上學者的研究常采用簡化的車橋動力分析模型或移動力來求解高架橋墩頂反力，較少考慮高速鐵路列車、軌道和橋梁相互作用特征。

時瑾等[8]將鋼軌模擬為離散點支撐歐拉梁，橋梁采用模態綜合法建立運動方程，在考慮梁-軌和輪-軌關系基礎上建立了車橋動力分析模型，并結合常用跨度簡支箱梁特點，分析了軌道不平順、速度和跨度對墩頂動反力的影響規律。但是，該文獻以某一確定軌道不平順樣本作為輪軌激擾輸入，沒有考慮軌道不平順隨機性引起的墩頂動反力統計學特征。 Lu等[9]指出軌道不平順是一個隨里程變化的隨機過程，由此引起的列車-結構耦合振動也是一個隨機過程，應該采用隨機振動的方法進行研究。王貴春等[10-11]研究表明，基于少量樣本的時程分析結果，通過統計處理來判別列車、結構的動力性能缺乏可靠性。Zhu等[12]對比分析了Monte Carlo法和虛擬激勵法(Pseudo-Excitation Method, PEM)的計算精度和效率，研究發現，PEM方法具有更高的計算效率和計算精度。

因此，本文基于PEM和有限元分析方法，建立列車-軌道-橋梁耦合時變系統豎向隨機動力學模型。以CRH2列車通過五跨32 m預應力混凝土簡支箱梁橋為例，分析了墩頂動反力隨機特征，并研究了軌道不平順譜種類和列車運行速度對墩頂動反力隨機特征的影響。為以后進一步研究環境振動、墩頂動剛度以及支座參數提供前期研究積累。

1 列車-軌道-橋梁動力學模型

1.1 列車模型

由于墩頂動反力主要由列車垂向作用引起，故本文僅考慮列車豎向振動自由度，每節車共有10個自由度。列車的運動方程如式(1)所示

(1)

式中:Mv，Cv,Kv,Xv分別為列車子系統質量矩陣、阻尼矩陣、剛度矩陣和位移列向量;Fv為列車子系統的外荷載列向量。

1.2 軌道-橋梁模型

在車橋耦合系統相互作用研究中，為降低計算工作量，常采用模態疊加法建立橋梁動力方程[13]。考慮軌道結構時，通常在選取模態時難以全面考慮軌道結構局部高頻振動模態，從而無法準確計算鋼軌局部振動以及輪軌之間的相對位移。采用有限元直接剛度法組裝整體剛度矩陣時，由于不存在人為設定分析截止頻率問題，計算精度較高。因此，本文采用有限元直接剛度法建立如下所示的軌道-橋梁系統動力方程

(2)

式中:Mb，Cb,Kb,Xb分別為軌道-橋梁子系統的總體質量矩陣、阻尼矩陣、剛度矩陣和位移矩陣，可以直接從通用有限元軟件ANSYS中直接導出[14]。其中阻尼矩陣Cb包括橋梁阻尼和軌下彈簧-阻尼器單元阻尼，采用Rayleigh阻尼來模擬橋梁結構的阻尼特性，阻尼比取2%[15]。Fb為軌道-橋梁子系統所受外力列向量。建立的車-軌-橋動力分析模型如圖1所示。

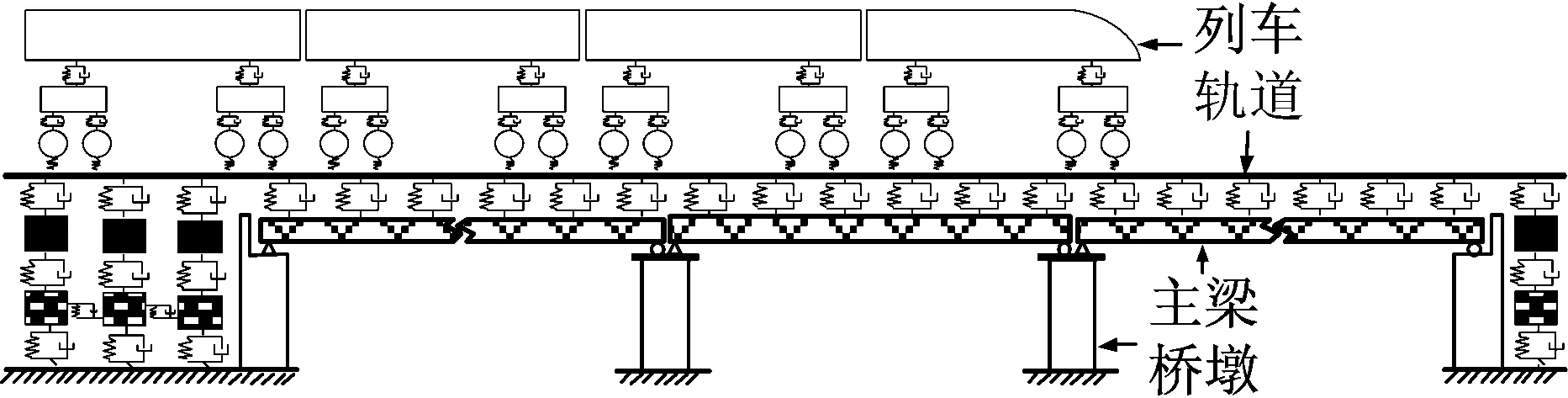
圖1 列車-軌道-橋梁耦合振動模型

1.3 軌道不平順模型

為分析不同軌道不平順條件對車致墩頂垂向動反力的影響，本文采用我國高速鐵路無砟軌道不平順譜(Chinese High-Speed Railways Ballastless Track Irregularity Spectrum, CHBI)、美國六級軌道譜(Federal Railroad Administration (FRA) Track Class 6, FAR6)、德國低干擾軌道譜(German Track Spectrum of Low Irregularity, GLI)和德國高干擾軌道譜(German Track Spectrum of High Irregularity, GHI)高低不平順作為輪軌激勵輸入。其中，FAR6，GLI和GHI的具體表達式可參考文獻[16]。CHBI則根據我國規范《高速鐵路無砟軌道不平順譜》(TB/T 3352—2014)的規定，采用分段擬合方式得到適用于我國線路速度300～350 km/h的高速鐵路無砟軌道不平順譜。

1.4 輪軌接觸模型

列車子系統和軌道-橋梁子系統之間通過輪軌接觸關系實現耦合作用。目前處理輪軌垂向接觸關系主要存在兩種方法[17]：一種是忽略輪軌相對變形的密貼模型；另一種是考慮輪軌相對變形的Hertz接觸模型。

密貼模型雖然理論上較為簡單，但由于其忽略了輪軌之間的相對變形而難以真實反映輪軌之間的動態相互作用。因此，本文采用線性Hertz接觸模型模擬輪軌關系，其中輪軌接觸剛度系數根據式(3)求解[18]

(3)

式中:G為輪軌接觸常數，m/N2/3；P0為靜輪重，N。

2 基于虛擬激勵法的墩頂動反力計算

2.1 列車-軌道-橋梁耦合時變系統隨機振動分析

將列車子系統和軌道-橋梁子系統通過輪軌接觸關系組成整體耦合時變系統，可建立列車-軌道-橋梁耦合時變系統動力方程

(4)

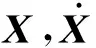
列車-軌道-橋梁耦合系統所受外荷載F(t)包括列車自重引起的確定性荷載Fg和軌道不平順引起的隨機性荷載Fr(t)，即

(5)

基于隨機振動理論，可將隨機激勵Fr(t)表示為

Fr(t)=Γ(t)G(t)x(t)

(6)

G(t)=

diag[g(t-t1)] …g(t-tj) …g(t-tn)

(7)

x(t)=

[x(t-t1) …x(t-tj) …x(t-tn)]T

(8)

式中：Γ(t)為作用力指示向量；G(t)為慢變均勻調制函數矩陣；x(t)為軌道不平順引起的多點異相位平穩隨機激勵向量；n為列車子系統輪對總數。

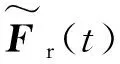
(9)

V(t)=diag[e-iωt1… e-iωtj… e-iωtn]

(10)

Q=[1 … 1 … 1]T

(11)

可快速獲得系統隨機響應的功率譜密度矩陣Suu(ω,t)

(12)

其中,

(13)

式中:h(t-τ,τ) 為脈沖響應函數；Sxx(ω)為x(t)的自譜密度矩陣。最后，根據隨機響應的功率譜密度矩陣，可通過下式求得系統隨機響應的均方根

(14)

式中：Δω為頻率增量。

考慮由車輪間距所產生的輪軌間隨機激勵相位差，第j(j=1～n)輪對由軌道不平順引起的虛擬軌道不平順rj可以表示為

(15)

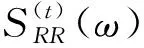
(16)

式中：ω為軌道不平順的時間圓頻率，rad/s；λ為軌道不平順函數諧波分量的波長，m。

2.2 墩頂動反力

列車行駛過程中，橋墩墩頂垂向動反力F可寫為

F=KZΔx+CzΔv

(17)

式中:KZ為墩頂彈簧阻尼器豎向剛度；Cz為阻尼系數；Δx和Δv分別為彈簧阻尼器頂端與底部位移之差和速度之差。高速鐵路常用支座類型有盆式橡膠支座、球形鋼支座及特殊要求支座等，支座系統本身力學行為復雜。文獻[19]研究表明，不同的支座恢復力模型對動載豎向力傳遞影響不大；文獻[20]指出實際彈性支座計算條件下，支座彈性對橋梁和車體的振動影響不明顯，因此本文模型中支座采用了剛性支撐。根據2.1節可求得墩頂動反力F的隨機響應均值μF與隨機響應均方根σF。

工程設計中，隨機響應最大值通常為重點關注對象。本文采用3σ法則(即μ±3σ)確定列車-軌道-橋梁耦合系統墩頂動反力隨機特征的上、下限值。同時，根據上述列車-軌道-橋梁耦合時變系統隨機分析方法，本文開發了相應的MATLAB計算程序，具體計算流程如圖 2所示。

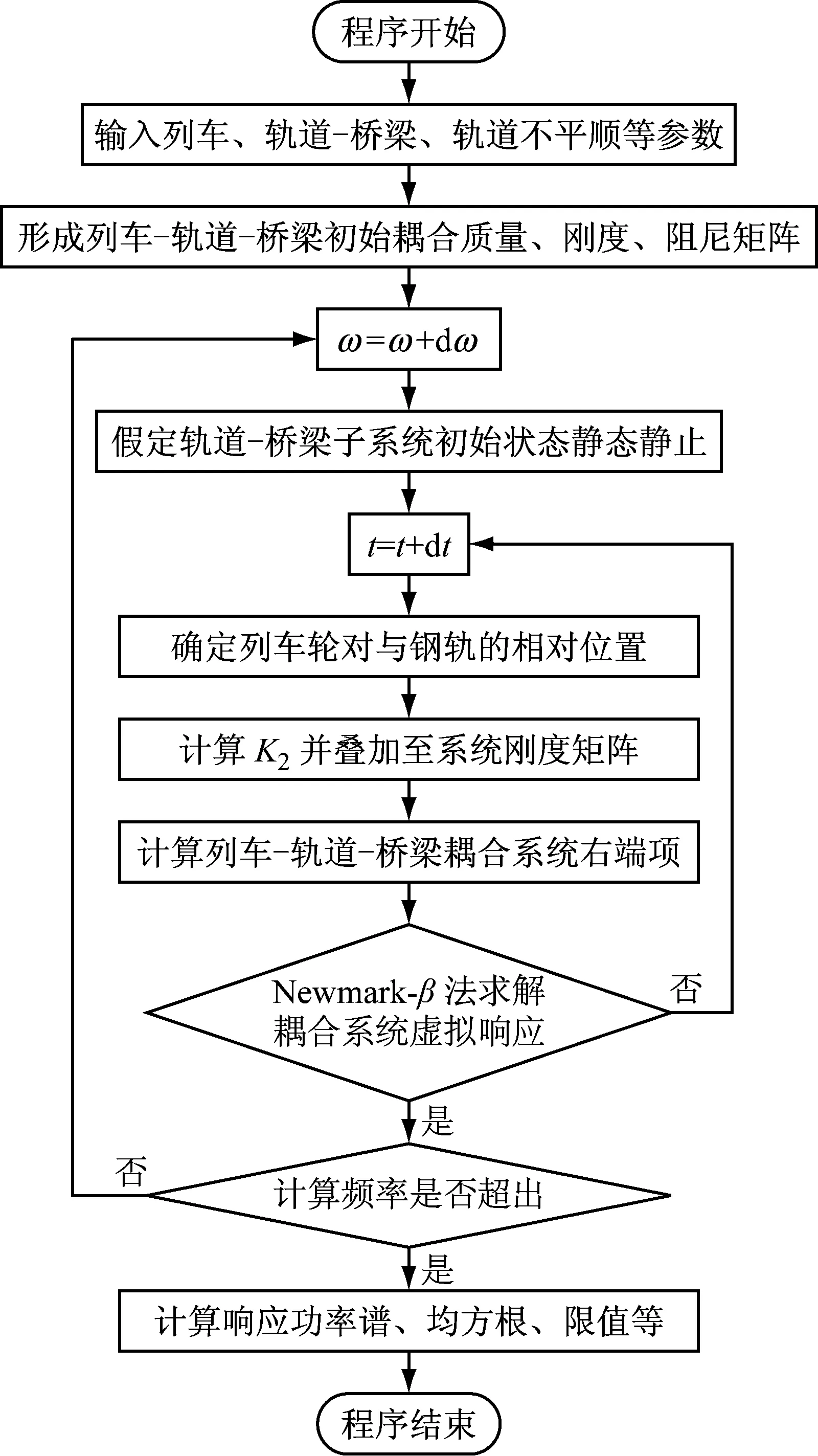
圖2 基于虛擬激勵法的車-橋耦合系統隨機振動分析流程圖

3 算例驗證

3.1 軌道-橋梁整體有限元模型

以我國高速線路總里程中占比最大的32 m標準跨度雙線單箱型截面預應力混凝土簡支梁橋為研究對象，橋梁鋪設雙塊式無砟軌道，雙塊式無砟軌道主要由鋼軌、扣件、預制的雙塊式軌枕、混凝土道床板等組成。雙塊式無砟軌道中，軌道的彈性主要靠軌下膠墊來提供。由于軌枕和混凝土道床板完全聯結在一起，軌下基礎的質量很大，道床板與混凝土底座之間基本沒有彈性，故雙塊式無砟軌道的振動主要體現在鋼軌的振動，而軌枕和道床板的作用可通過參振質量的形式在橋梁動力學模型中加以考慮。因而將軌道板與橋梁考慮為整體進行模擬，鋼軌和橋梁間通過等間距布置的扣件相連接，將軌下結構對鋼軌的支撐作用采用軌下支撐彈簧模擬。

采用有限元方法建立如圖 3所示的無砟軌道-橋梁模型，主梁和橋墩截面如圖 4所示。在有限元模型中，鋼軌、主梁和橋墩均采用空間梁單元模擬。為了考慮橋梁的高頻振動，本文主梁單元長度為0.6 m，保持與扣件間距一致，軌道結構節點和橋梁節點在扣件位置處一一對應，按節點位移協調處理。線路偏心通過剛臂考慮，鋼軌節點和剛臂節點之間采用彈簧-阻尼器聯結，考慮軌下扣件和墊板的彈性支撐作用，垂向剛度和阻尼分別為4.76×107N/m和7.5×104N·s/m，橫向剛度和阻尼分別為2.5×107N/m和6×104N·s/m，橋面二期恒載取160 kN/m。

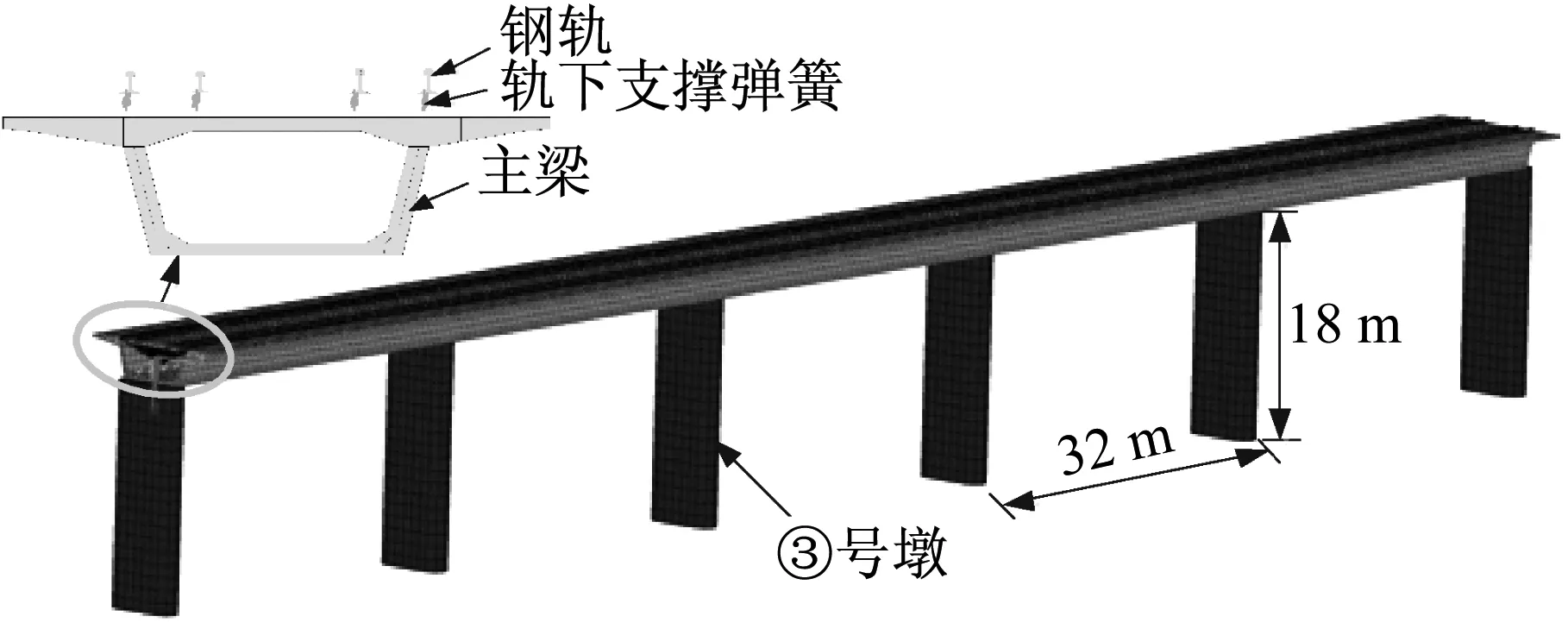
圖3 軌道-橋梁系統有限元模型

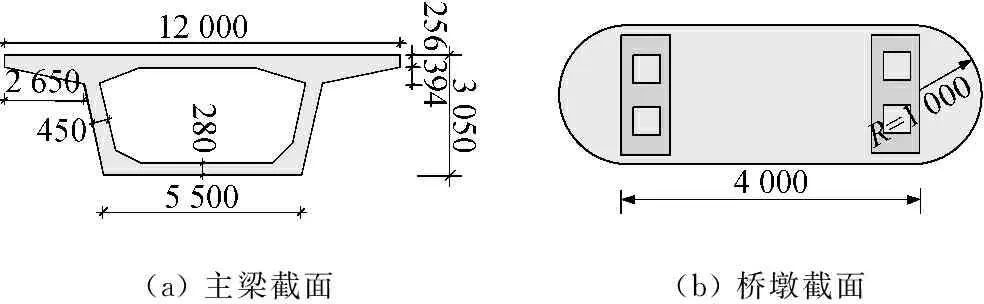
(a) 主梁截面(b) 橋墩截面

圖4 橋梁截面示意圖(單位：mm)

Fig.4 Schematic diagram of bridge section (unit: mm)

3.2 驗 證

參考文獻[21]，采用自編程序開展ICE3高速列車通過該橋梁模型的車-橋耦合振動響應計算。列車編組模式為按8車編組(2M+6T)，頭車和尾車為軸重較大的動車，其余6輛均為軸重較小的拖車，列車詳細參數見朱志輝等的研究，行車速度為250 km/h，輪軌間激擾采用由德國高速鐵路低干擾譜變換出的軌道不平順時域樣本。將計算結果與文獻[21]的結果進行對比來驗證模型及程序的正確性。

圖 5和圖 6分別給出了圖 3中③號橋墩墩頂垂向位移和垂向加速度的結果，從圖中可以看出本文和文獻[21]的結果在幅值和趨勢上吻合良好。其中由于原文沒有給出詳細的列車、軌道、橋梁參數，本文算例中所選取車-線-橋模型相關參數與文獻[21]存在差別，導致本文的墩頂垂向位移偏小。總體而言，本文計算方法能夠較好的反映車-軌-橋耦合振動特性，滿足工程應用要求。

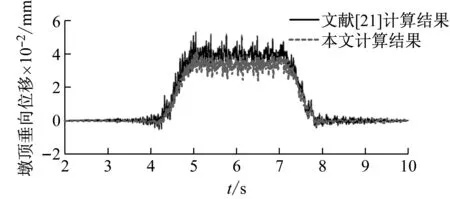
圖5 橋墩墩頂垂向位移

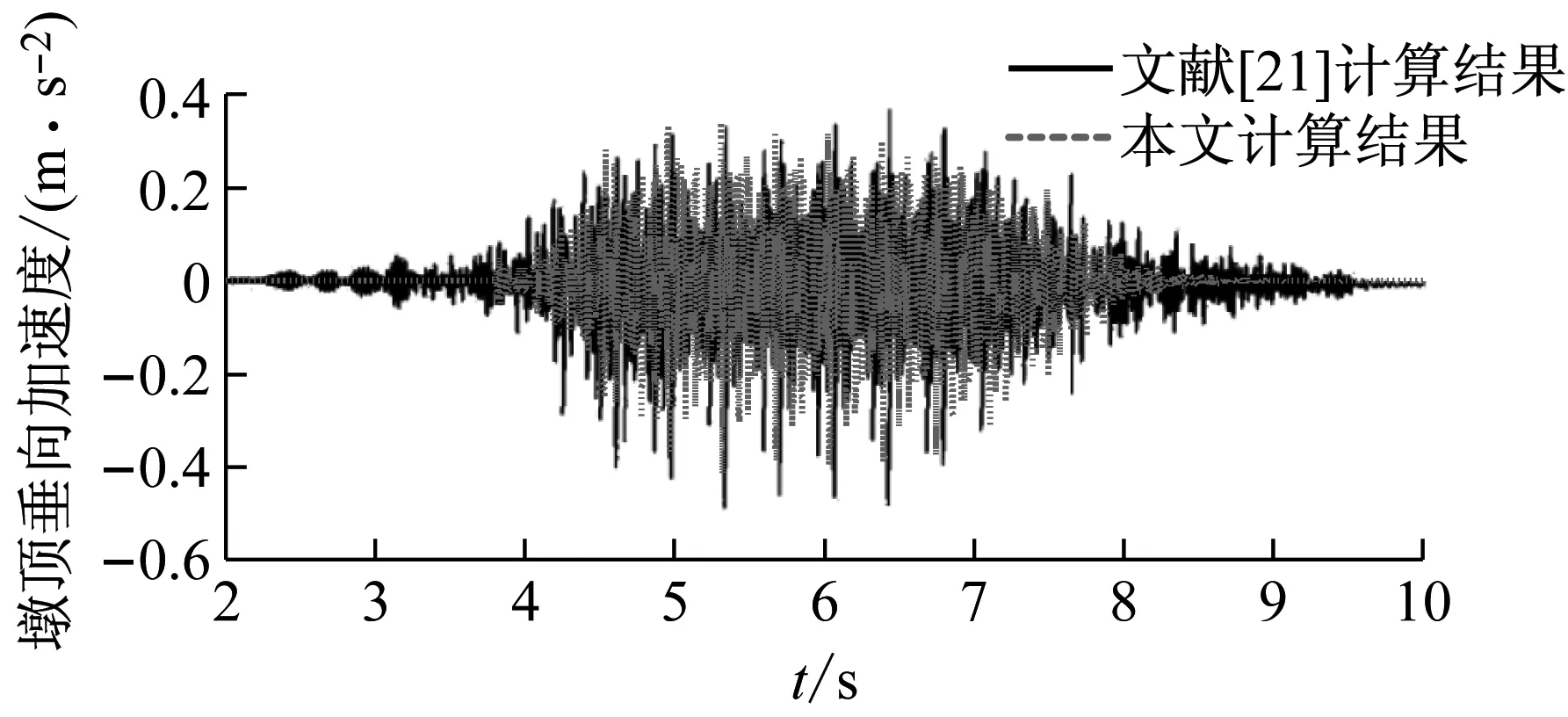
圖6 橋墩墩頂垂向加速度

4 計算結果與分析

4.1 墩頂動反力隨機特性分析

基于列車-軌道-橋梁耦合系統隨機動力學模型，選取八車編組CRH2列車以300 km/h的速度單線通過簡支梁的計算結果，對墩頂垂向動反力的隨機特征進行研究。其中軌道不平順為德國低干擾軌道不平順譜，波長范圍為1～100 m，相應的頻率計算范圍為0.833～83.3 Hz，頻域積分步長為0.833 Hz。以圖 3中的③號墩為例，橋墩頂部受到墩頂動反力F1,F2作用，如圖 7所示。

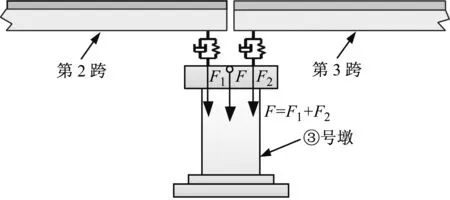
圖7 ③號墩墩頂動反力示意圖

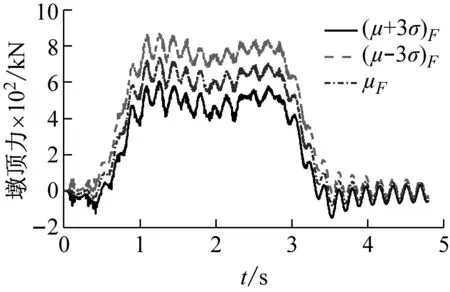
圖 8給出了3號墩墩頂動反力F1，F2以及合力F的統計參數時程曲線。其中μ為不考慮軌道不平順時車-橋耦合振動引起墩頂動反力均值，σ為軌道不平順引起的墩頂動反力均方根，(μ±3σ)為基于3σ法則的墩頂動反力上、下限值。

從圖 8可以看出

(1) 墩頂動反力受確定性激勵(列車軸重)控制，其中隨機激勵引起的墩頂動反力均方根σ最大值約為確定性激勵引起的墩頂動反力均值μ最大值的8%。

(2) 從圖 8(c)中可知，根據3σ法則計算的墩頂動反力下限值(μ-3σ)F和上限值(μ±3σ)F的最大值分別為606.18 kN和875.37 kN，變化幅度為269.19 kN；相對于墩頂動反力均值μF最大值的變化在-17.76%～18.76%。

(3)F1和F2的動力響應指標(均值與均方根)差別很小，振動趨勢類似，但是由于列車通過相鄰兩跨簡支梁的時間先后不同，F1和F2的動力響應之間存在一定的相位差，因此合力F和分力F1,F2之間的統計參數不具有簡單的倍數疊加關系。

為了節省篇幅，只選取第3跨簡支梁對③號墩引起的墩頂動反力F1做頻域分析。通過對圖 8 (a)中的F1做快速傅里葉變換(Fast Fourier Transformation, FFT)，可以得到F1均值(μF1)的功率譜密度(Power Spectral Density Function, PSD)曲線，如圖 9所示；圖 10中給出了基于虛擬激勵法得到的隨機激勵下F1的時變PSD云圖。

從圖 9可知，當車速為300 km/h時，主頻f1=0.208 Hz，(1/f1)與列車通過全橋的加載時間t一致；同時，列車車長加載頻率fv=f2(fv=v/lv=3.27 Hz[22]，

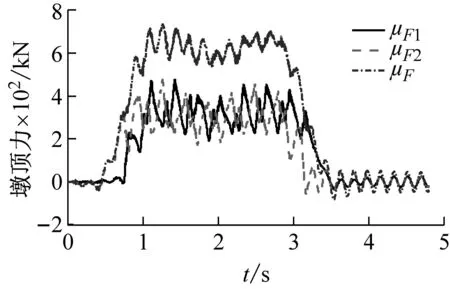
(a) μ

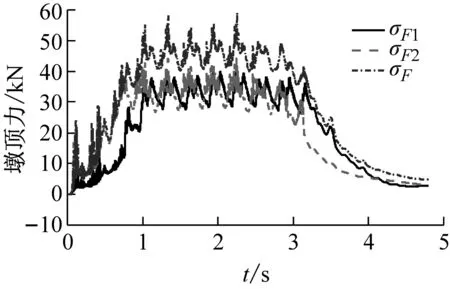
(b) σ

(c) μ±3σ

v和lv分別為車速和列車長度)，說明列車車長的周期性激勵對墩頂動反力影響較大。從圖 10可知，隨機荷載激勵下墩頂動反力的主頻大致分布在兩個連續的寬頻0.83～8 Hz和25～48 Hz內，分別與列車車長引起的周期性加載頻率(fv=3.27Hz)，列車軸距引起的周期性加載頻率(ft=v/lt=3.3 Hz，lt為列車軸距)密切相關。

4.2 軌道不平順對墩頂動反力的影響

由上一節分析可知，軌道不平順對墩頂動反力影響顯著，因此本節通過對比相同車速(300 km/h)條件下，不同軌道不平順譜引起的墩頂動反力隨機響應特征，研究軌道不平順對墩頂動反力的影響規律。

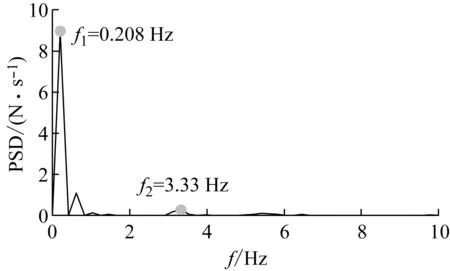
圖9 確定激勵下F1的PSD

表 1給出了不同軌道不平順下F1的統計參數最大值，圖 11～圖 13分別給出了不同軌道不平順隨機激勵下F1的均方根(σ)和限值(μ+3σ)的時程曲線以及PSD云圖，從表 1和圖 11～圖 13的結果中可知

(1) 我國高速鐵路無砟軌道不平順譜引起的墩頂動反力離散性最小，德國高干擾軌道譜引起的墩頂動反力離散性最大，二者均方根(σ)最大值相差40.79 kN，表明軌道不平順等級越低，墩頂動反力離散性越大；二者墩頂動反力(μ+3σ)最大值相差26.68%。

(2) 不同軌道不平順下墩頂動反力的均方根時程曲線波形相似，只是幅值大小不同，說明盡管軌道不平順等級不同，但是列車經過橋梁時，對墩頂動反力造成的離散性隨時間的變化規律是一致的。

(3) 比較不同軌道不平順隨機激勵下F1的PSD

云圖可知，4種軌道不平順下的墩頂動反力主頻分布類似，大致分布在兩個連續的寬頻范圍內，說明同一行車條件下，不同軌道不平順對墩頂動反力有影響的波長范圍相似。

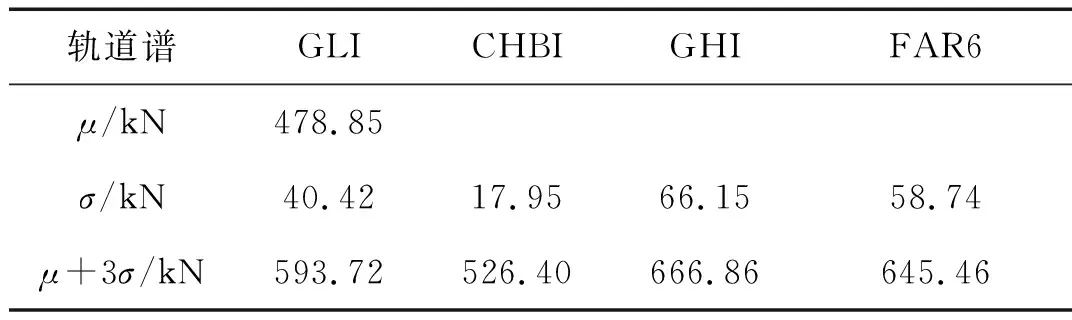
表1 不同軌道不平順下統計參數最大值

圖11 σF1

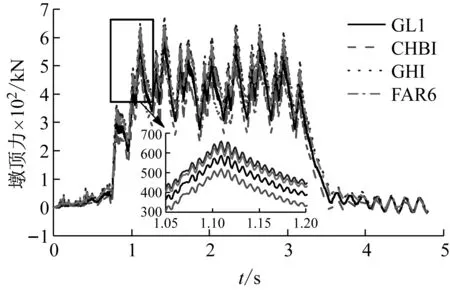
圖12 (μ+3σ)F1

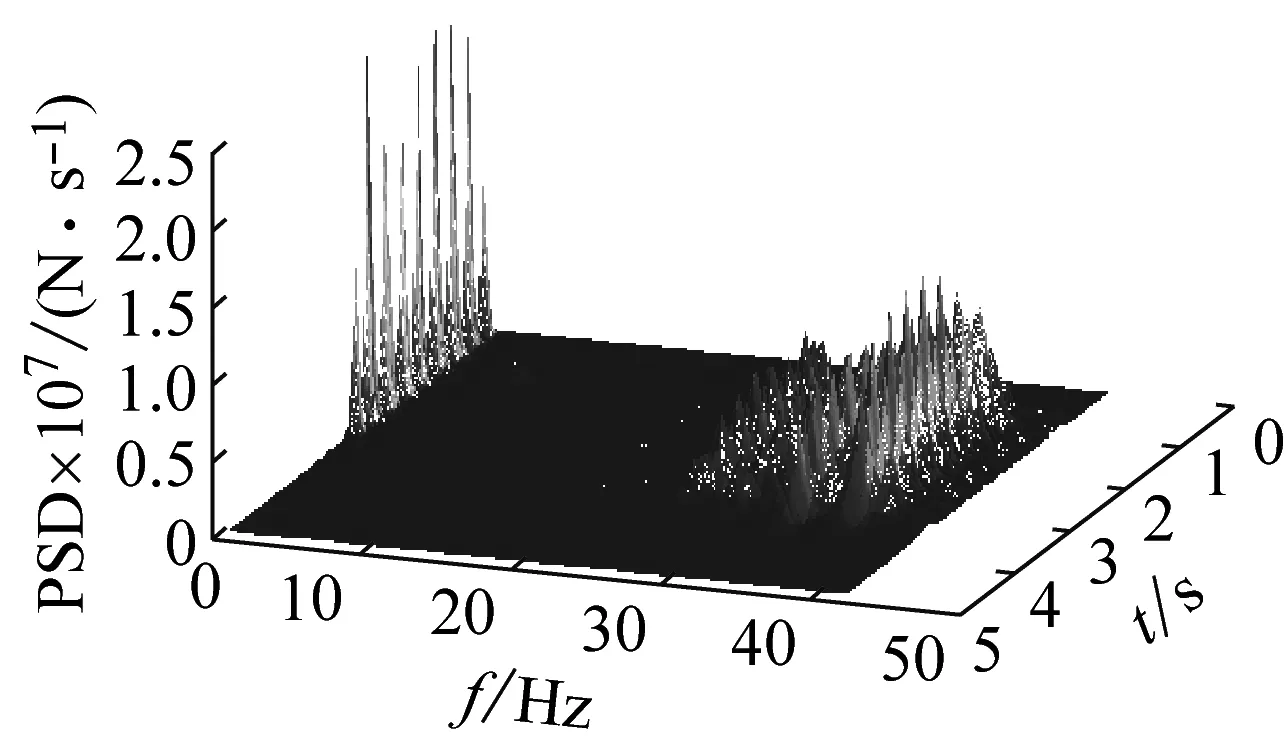
(a) CHBI

(b) GHI

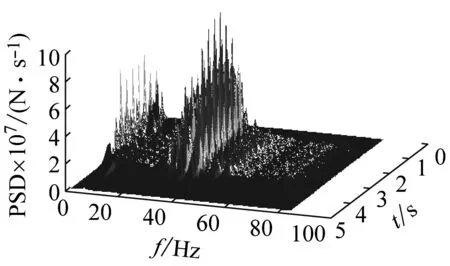
(c) FAR6

4.3 列車運行速度對墩頂動反力的影響

列車運行速度對車橋耦合系統的動力響應影響顯著，為研究墩頂動反力隨機特征隨車速的變化規律，選取軌道不平順為德國低干擾，列車以100～500 km/h(按12.5 km/h遞增)之間33種不同車速通過簡支梁的計算工況來分析。圖 14和圖 15分別給出了F1的統計參數最大值隨車速變化規律和不同車速軌道不平順隨機激勵下F1的PSD云圖；表 2則給出了不同車速下F1的統計參數最大值。

從圖 14、圖 15以及表 2的結果中可知

(1) 隨著車速的增大，由車-橋耦合振動引起的共振和消振導致橋梁墩頂動反力均值(μ)的最大值被放大和縮小。墩頂動反力限值(μ+3σ)主要受確定性激勵響應(μ)控制，所以其隨車速的變化規律與均值(μ)類似。

(2) 墩頂動反力均方根(σ)隨著車速的增大而顯著增大，當車速從100 km/h增大到500 km/h，均方根從12.6 kN增大到100 kN，表明車速越大，軌道不平順的影響越大，墩頂動反力的離散性越大。

(3) 車速為100 km/h時，軌道不平順隨機激勵下F1的主頻分布在0.28～1.39 Hz內，車速為400 km/h時，的主頻則分布在1.11～70 Hz內。可以發現車速較小時，墩頂動反力主頻主要集中分布在一個低頻范圍內，只有長波不平順對其有影響；而隨著車速的增大，墩頂動反力主頻分布漸漸向高頻擴展，趨向于在一個連續的寬頻范圍內均勻分布，短波不平順的影響有所體現。

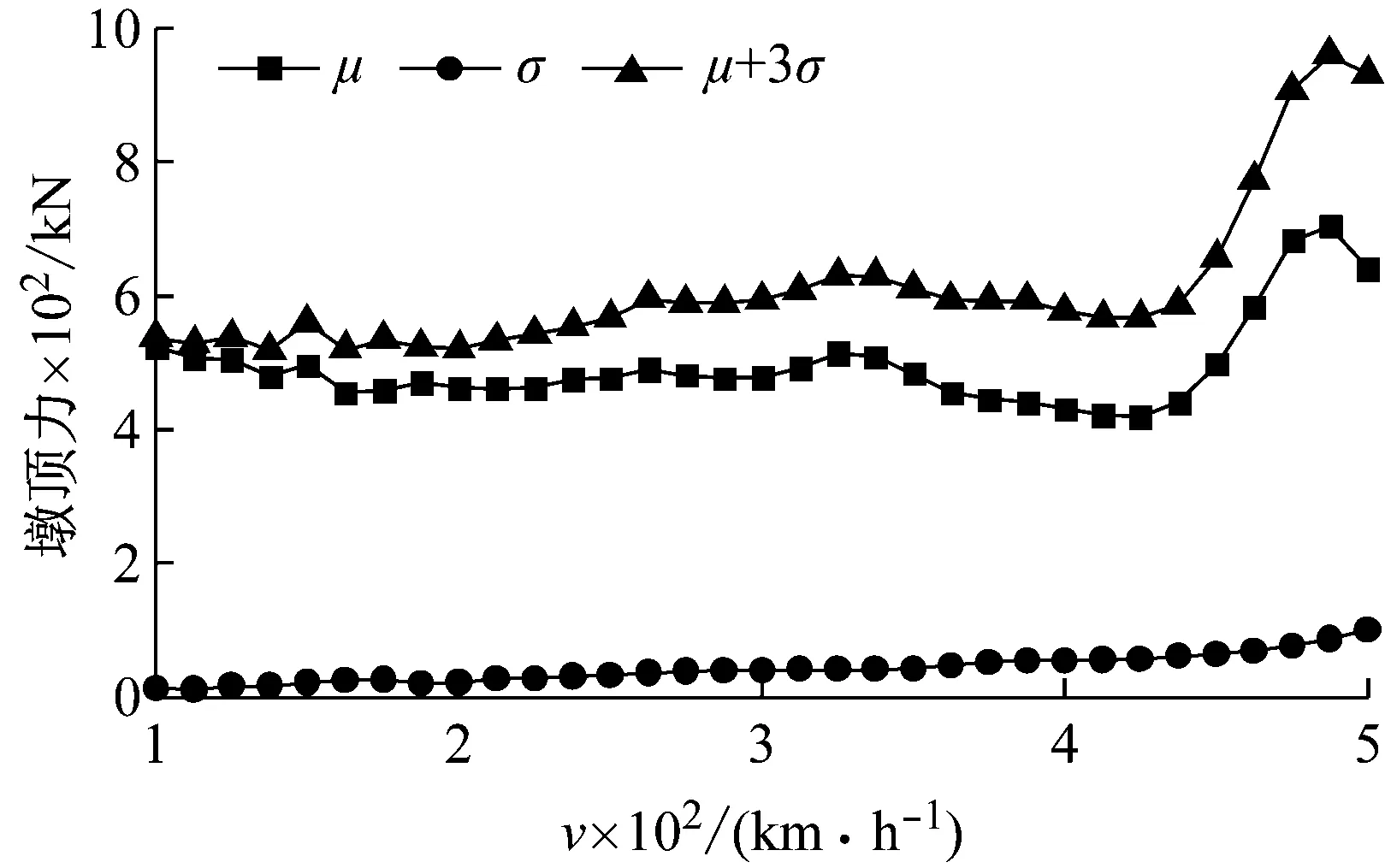
圖14 F1的統計參數最大值隨車速變化規律

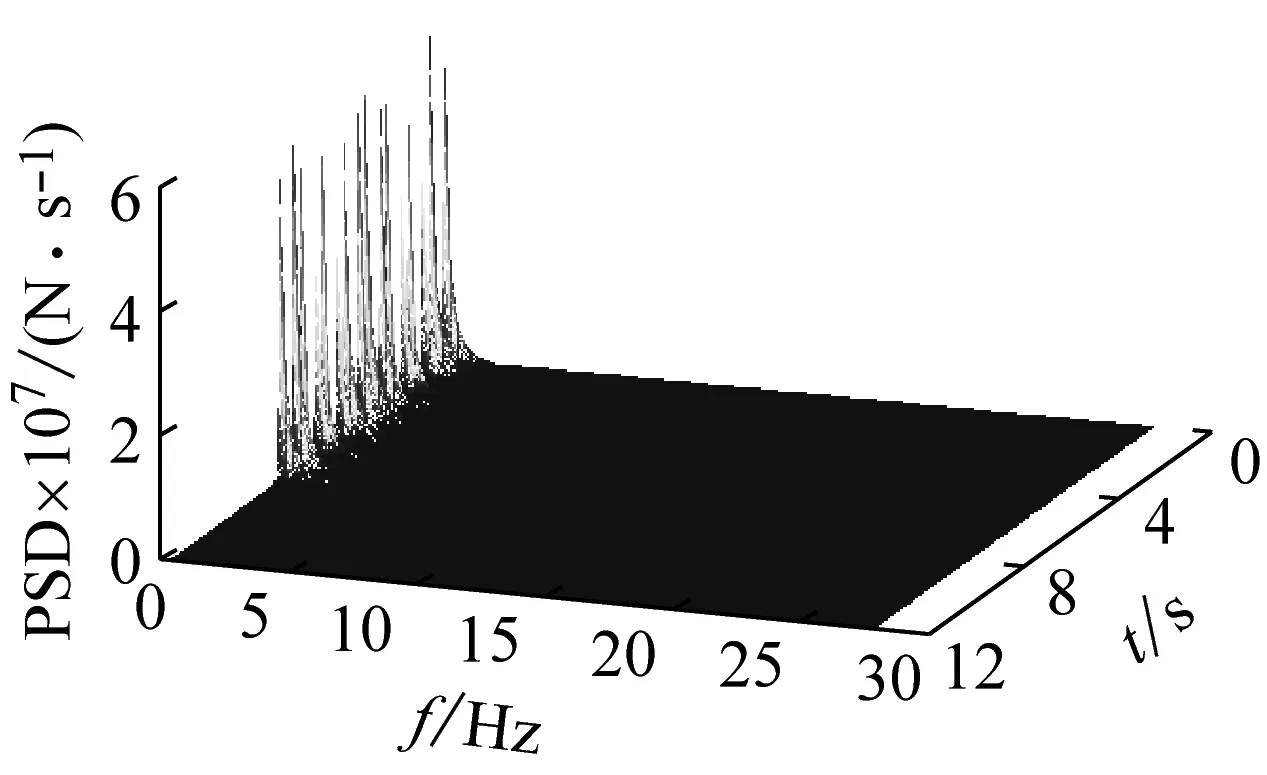
(a) 100 km/h

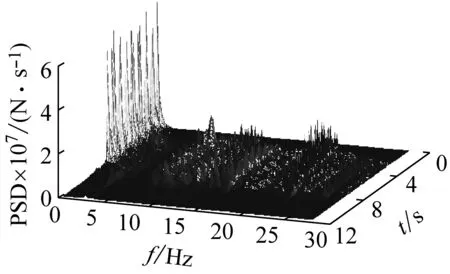
(b) 200 km/h

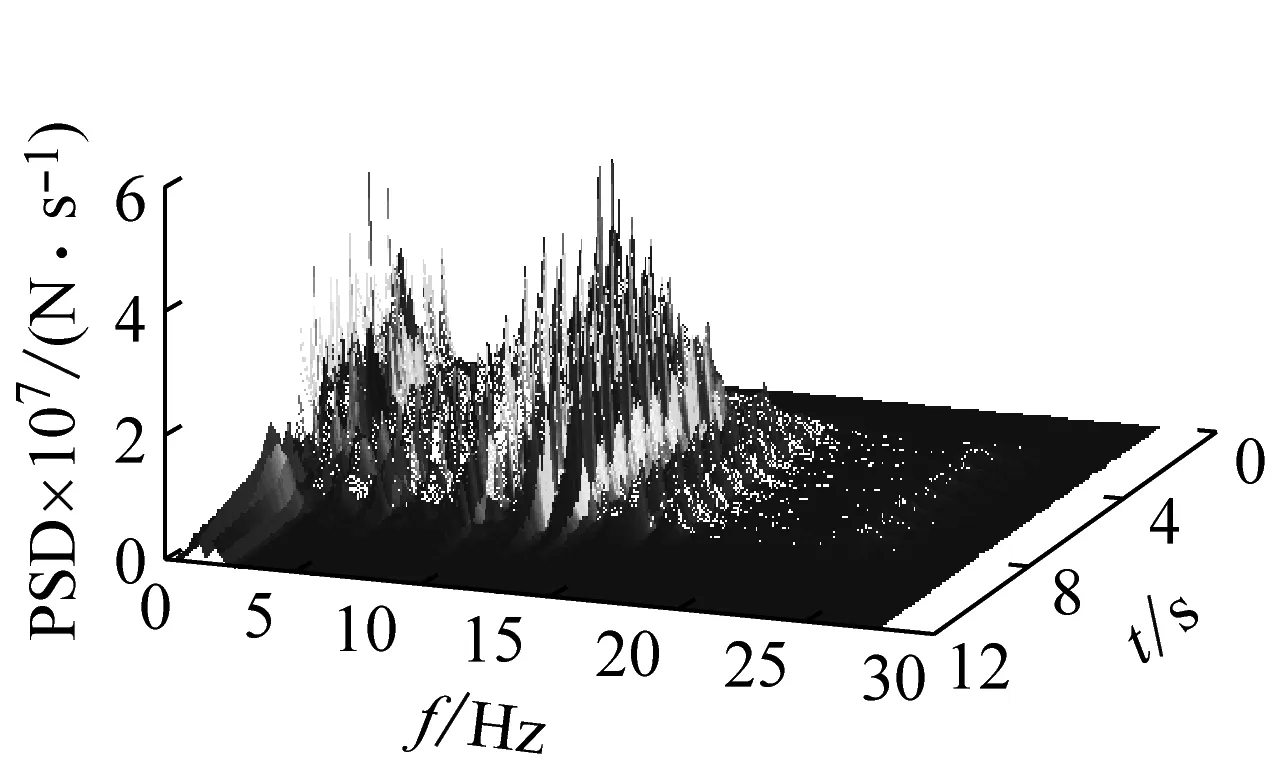
(c) 400 km/h

速度/(km·h-1)100150200250300350400450500μ/kN522.4497.2463.4477.7478.9484.1430.1498.7641.0σ/kN12.621.821.732.040.443.355.063.7100.0μ+3σ/kN536.5 560.5521.2568.4593.7610.6577.9658.4930.7

5 結 論

本文基于虛擬激勵法和有限元法，建立了列車-軌道-橋梁耦合系統豎向隨機振動模型，并以CRH2列車通過我國高速線路占比最大的32 m預應力混凝土簡支箱梁橋為算例，對墩頂垂向動反力隨機特性以及軌道不平順種類和車速對其影響規律進行了研究，得出了如下結論：

(1) 建立了列車-軌道-橋梁耦合系統豎向隨機振動模型，可以全面考慮軌道不平順引起的隨機振動，得到墩頂動反力的均值、均方根和限值等統計指標；墩頂動反力受列車軸重確定性激勵和軌道不平順隨機激勵的雙重影響，且受軌道不平順的影響顯著，任意時刻的墩頂動反力并非確定值，而是介于下限值(μ-3σ)和上限值(μ+3σ)之間。

(2) 不同軌道不平順下，墩頂動反力的均方根(σ)大小不同，軌道不平順等級越低，離散性越大；隨機激勵下的墩頂動反力PSD云圖主頻分布類似。

(3) 隨著車速的增大，由車-橋耦合振動引起的共振和消振導致橋梁墩頂動反力均值(μ)的最大值被放大和縮小，特別是共振條件下，墩頂動反力峰值變化劇烈；墩頂動反力均方根(σ)受車速影響顯著,車速越大，墩頂動反力離散性越大，從而導致根據3σ法則得到的墩頂動反力限值越大。