連鑄結晶器非正弦振動裝置建模與固有特性分析
周 超 張興中 劉平飛 關 杰
1.燕山大學國家冷軋板帶裝備及工藝工程技術研究中心,秦皇島,066004
2.河北農業大學海洋學院,秦皇島,066003
3.中國重型機械研究院有限公司,西安,710032
0 引言
結晶器非正弦振動在提高拉坯速度、有效地避免黏結性漏鋼、提高鑄坯質量等方面效果明顯,因此研究結晶器非正弦振動對實現高效連鑄具有重要的意義[1]。
結晶器非正弦振動的核心是振動裝置,目前工業上應用的結晶器振動驅動裝置主要有3種:液壓驅動系統、伺服電動缸驅動系統和機械驅動裝置。液壓驅動系統能夠方便地實現任意振動波形及參數的在線調整,但系統比較復雜,且投資及維護費用較高[2]。伺服電動缸驅動裝置由鐳目公司開發[3],可以實現振幅、頻率和波形偏斜率的在線調節,但伺服電機頻繁的正反轉影響位移、速度等的跟蹤精度以及系統響應速度,同時,滾珠絲杠的承載能力難以與液壓裝置及曲柄機構相媲美。PARK等[4]將偏心軸部分做成凸輪輪廓,零件一旦制造出來,波形、振幅和波形偏斜率都不能調節,且三角形、矩形波等速度突變較大的波形都不能實現。機械驅動裝置結構簡單、成本低、便于維護、可靠性好。張興中等[5]開發的橢圓形齒輪驅動結晶器非正弦振動裝置具有良好的工藝特性和動力學特性,但齒輪嚙合時的齒側間隙產生嚙合沖擊和噪聲,齒輪的偏心質量引起裝置運動不平穩。ZHANG等[6]開發的逆平行四連桿驅動結晶器非正弦振動裝置產生波形的原理與橢圓齒輪相同,雖可避免齒輪嚙合帶來的沖擊和噪聲,但機構的傳動鏈依然很長。張興中等[7]開發的雙偏心驅動結晶器非正弦振動裝置的振動頻率在線可調,振幅停機可調,結構簡單、加工容易、投資少,但對加工精度要求較高。與液壓驅動系統相比,上述機械式驅動裝置的波形偏斜率都不能在線調節。
為克服上述裝置的缺點,本文設計出一種雙伺服電機驅動的結晶器非正弦振動裝置,其頻率和波形偏斜率在線可調,振幅停機可調,能夠很好地使結晶器實現非正弦振動。與正弦振動相比,非正弦振動雖有良好的工藝特性,但運動的平穩性較差,因此,對非正弦振動系統的動力學研究有重要意義。本文對雙伺服電機驅動結晶器非正弦振動裝置進行研究,重點研究裝置固有特性的變化規律。
1 非正弦振動裝置
1.1 振動系統工作原理
雙伺服電機驅動結晶器非正弦振動系統主要由驅動裝置、緩沖彈簧、導向板簧、結晶器及振動臺等組成,如圖1所示。由于系統左右對稱,故取一半模型,其工作原理如圖2所示。工作時,伺服電機驅動減速器,減速器通過聯軸器連接偏心軸,通過電機變角速度運動,使偏心軸帶動連桿在S點的鉛垂方向上產生非正弦振動。在緩沖彈簧和導向板簧的作用下,連桿推動振動臺及其上的結晶器上下振動。
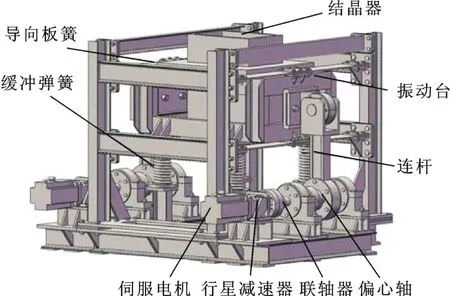
圖1 雙伺服電機同步驅動結晶器非正弦振動裝置Fig.1 Non”sinusoidaloscillator synch ronously d riven by double servomotors
1.2 運動學分析
德馬克非正弦振動波形的位移曲線表達式為[8]
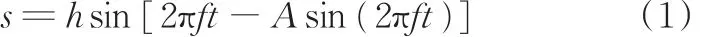
式中,h為振幅,mm;f為振動頻率,Hz;A為波形偏斜因子;t為時間,s。

圖2 非正弦振動系統工作原理Fig.2 W orking p rincip le diagram of non”sinusoidal oscillation system
如圖3所示,在一個振動周期內,非正弦振動波形的峰值滯后于正弦波形的峰值,可以推導出波形偏斜因子A和波形偏斜率α的關系。當s=h時,可得到位移峰值時間tc與A的關系:
h=h sin(2πftc-A sin(2πftc)) (2)

圖3 非正弦與正弦振動位移波形Fig.3 Disp lacem en twaveform of non”sinusoidal and sinusoidal oscillation
所以在一個振動周期[0,1/f]內,存在
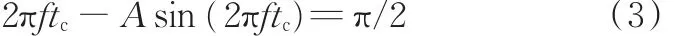
解得
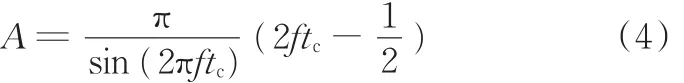
滯后時間

波形偏斜率
α =4f tm(6)
聯立式(5)、式(6)得

將式(7)代入式(4)解得

波形偏斜因子A和波形偏斜率α之間的關系見圖4。
在鉛垂方向上,連桿運動的位移與結晶器振動的位移一致,由二者的位移關系可得偏心軸角速度的表達式:


式中,ω為偏心軸的角速度,rad/s;e為偏心軸的偏心距,mm。
圖5給出了不同波形偏斜率下偏心軸的角速度曲線。只要偏心軸按某一特定的規律旋轉,即可實現德馬克非正弦振動波形。
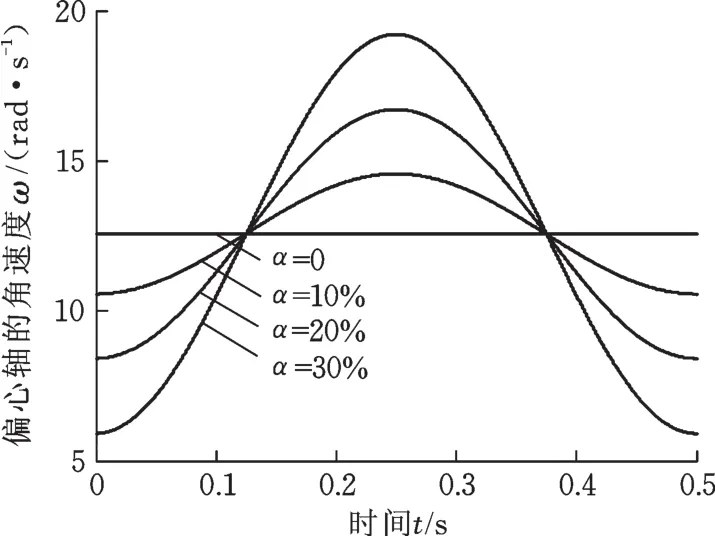
圖5 不同波形偏斜率下偏心軸角速度Fig.5 Eccen tric shaft angu lar velocity of d ifferent waveform deviation factors
由圖1建立非正弦振動裝置的剛柔耦合三維模型,取α=20%,f=2 Hz,h=5 mm,對裝置進行運動學仿真,得到德馬克非正弦振動波形,如圖6所示,從而驗證原理的正確性。
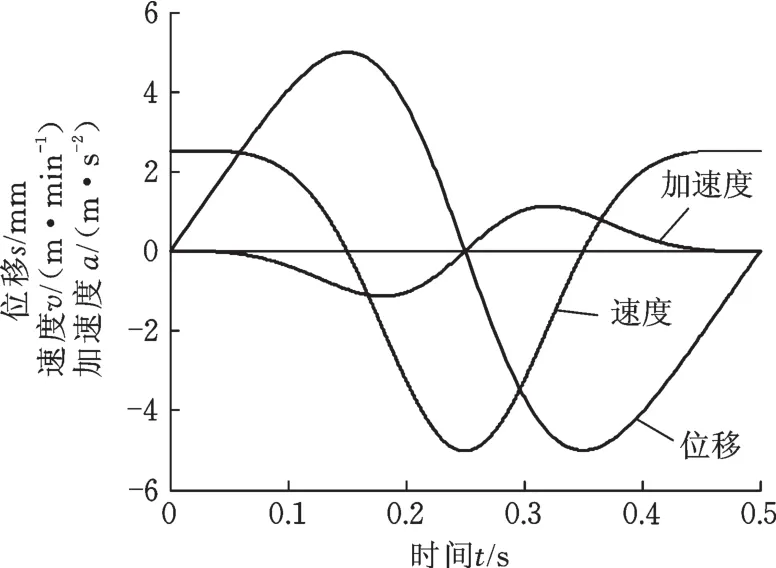
圖6 機構振動波形曲線Fig.6 Oscillation waveform ofm echanism
2 系統動力學模型的建立
根據非正弦振動系統中各構件的受力和變形特點,忽略曲柄、連桿、齒輪的彈性變形及運動部件間的間隙和摩擦,認為伺服電機運轉平穩可靠。伺服電機驅動結晶器非正弦振動系統動力學模型(圖7)是扭振和線振耦合模型,該模型把實際位移分解為靜態位移和彈性位移[9]。
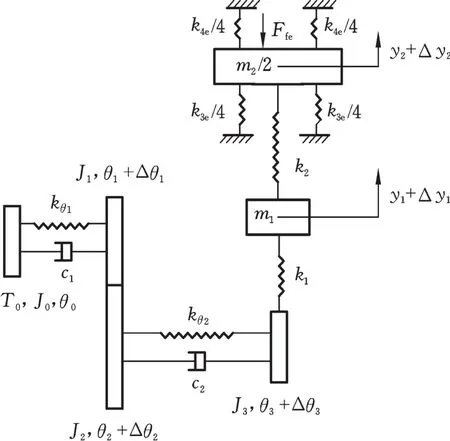
圖7 非正弦振動系統動力學模型Fig.7 Dynam icmodel of non”sinusoidal oscillation system
圖7中,T0為伺服電機輸出轉矩;J0為伺服電機輸出軸的轉動慣量;θ0為伺服電機輸出軸的角位移;kθi為扭轉剛度,i=1,2;k1、k2分別為連桿上下兩部分的抗壓剛度;ci為聯軸器阻尼系數;θj為轉動部件靜態角位移,j=1,2,3;Δθj為轉動部件彈性角位移;m1為連桿的質量;y1、y2分別為連桿及結晶器縱向的靜態位移;Δy1、Δy2分別為連桿及結晶器縱向的彈性位移;k3e為彈簧的彈性剛度;k4e為板簧的彈性剛度;m2為結晶器及振動臺的質量;Ffe為鑄坯與結晶器之間的摩擦力;J1、J2、J3分別為減速器的主動齒輪、從動齒輪及偏心軸的轉動慣量。
選取Δθ1、Δθ3、Δy1、Δy2為獨立廣義坐標,其他廣義坐標由所選取的廣義坐標來表示。由偏心軸的轉角與連桿縱向位移之間的關系可得
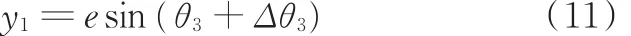
將式(11)展開得

偏心軸的轉角很小時,cosΔθ3≈ 1,sinΔθ3≈ Δθ3。代入式(12)得到
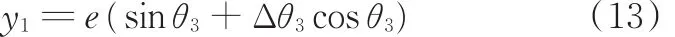
由于連桿與結晶器振動臺在鉛錘方向上的運動位移相同,故有y1=y2。
由非正弦振動系統各部件之間的運動學關系,可得各部件靜態位移之間的關系:θ0=θ1,θ2=θ3,y1=y2。
假設減速器為剛體,齒輪不變形,則減速器傳動比為
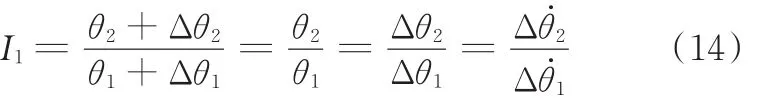
3 振動系統微分方程的建立
根據圖7建立的動力學模型及第2節中各參數之間的關系,采用帶阻尼的拉格朗日方程:
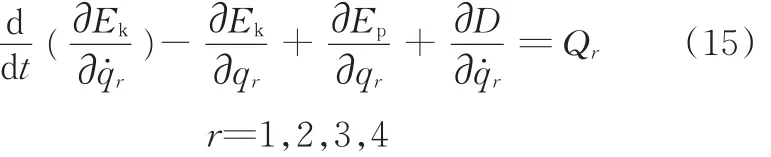
式中,Ek為振動系統的動能,J;Ep為振動系統的勢能,J;Qr為系統的廣義激振力,N;D為系統的廣義阻尼力,N;qr為系統的廣義坐標。
推導出該系統的運動微分方程。
根據系統的動力學模型和各部件運動參數之間的關系得到系統的動能、勢能及阻尼項:
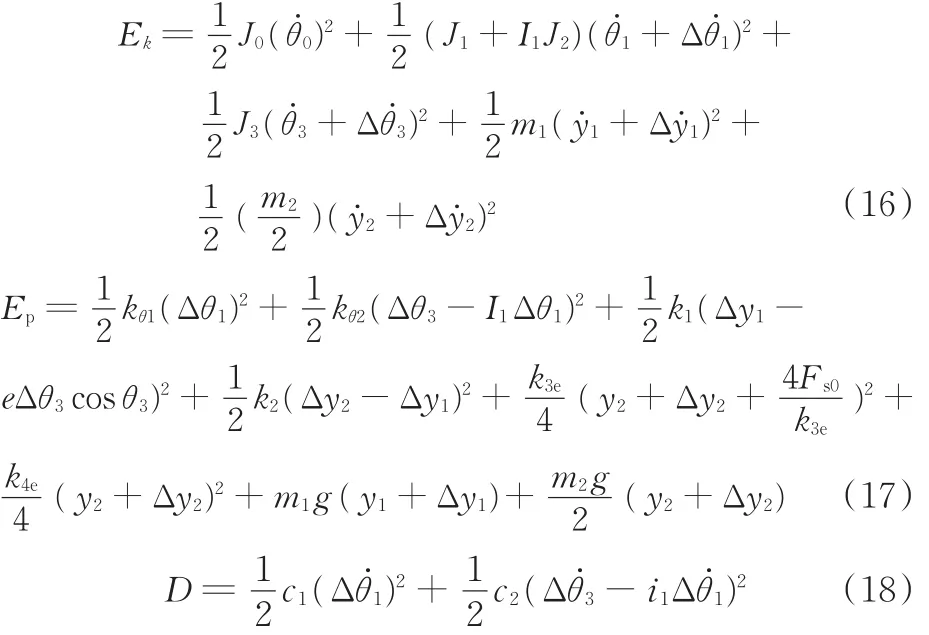
將式(16)~式(18)代入系統的微分方程式(15),得到系統受迫振動微分方程:

式中,M為質量矩陣;K為剛度矩陣;C為阻尼矩陣;F為廣義力向量;g為重力加速度,m/s2;Fs0為緩沖彈簧預緊力,N;q 為位移向量,q=(Δθ1,Δθ3,Δy1,Δy2)T;q˙為速度 向 量 ,q˙=(Δθ˙1,Δθ˙3,Δy˙1,Δy˙2)T;q¨為 加 速 度 向 量 ,q¨=(Δθ¨1,Δθ¨3,Δy¨1, Δy¨2)T。
由動力學參數之間的關系可知,伺服電機驅動結晶器非正弦振動系統的質量矩陣為常量,剛度矩陣、阻尼矩陣和激勵矢量都是隨時間周期變化的。
4 動力學分析
線性定常系統可采用多剛體系統動力學方法來求解其特征值和特征向量。雙伺服電機驅動結晶器非正弦振動裝置為周期時變參數系統[10?11],可通過瞬時機構凝固法求解其固有頻率。將轉角θ3在某一瞬間凝固,則系統的剛度矩陣變為常系數矩陣,采用結構動力學的方法來計算系統的固有頻率。計算所需系統的特征參數見表1。
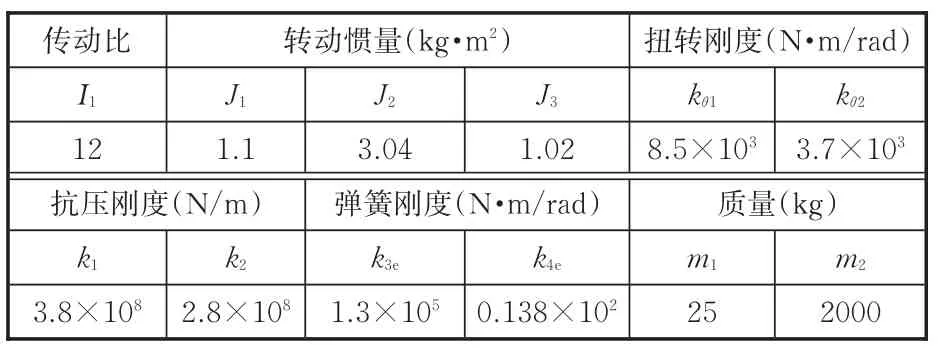
表1 系統的特征參數Tab.1 Characteristic parameters of the system
4.1 非正弦振動系統固有頻率
將式(19)轉變為如下的無阻尼自由振動系統:

即

式中,ωj為振動系統的固有角頻率,rad/s;fj為振動系統的固有頻率,Hz;φj為振動系統的特征向量。
本文采用瞬時機構凝固法對式(21)進行編程求解,得到系統的固有頻率。由非正弦振動系統動力學模型可知,固有頻率為偏心軸的轉角及振幅的函數,與結晶器振動的頻率及波形偏斜率無關。
4.1.1 偏心軸的轉角和振幅對固有頻率的影響
由圖8可以看出,系統的固有頻率是周期時變的,振幅較小時,各階固有頻率的波幅并不大,且隨振幅的增大,波幅變大。由于系統的固有頻率不受頻率和波形偏斜率的影響,因此調節頻率和波形偏斜率,可避免固有頻率的變化,擴大了參數的選取范圍,更有利于實現結晶器的最佳振動模式。
4.1.2 系統慣性參數對固有頻率的影響
對于非正弦振動系統,當結晶器振幅h=5 mm時,只改變各構件的慣性參數,其他參數保持不變,系統的固有頻率也將發生變化。以系統1階固有頻率為例進行說明。由圖9a可以看出,減速器的主動齒輪、從動齒輪的轉動慣量及連桿的質量對非正弦振動系統的固有頻率影響較小;結晶器及振動臺質量減小時,固有頻率略有增大。由圖9b可以看出,偏心軸的轉動慣量減半后,系統的固有頻率增加幅度較大,若要提高系統的固有頻率,只需適當減小偏心軸的轉動慣量。結晶器振動頻率遠離系統的固有頻率,有利于高效連鑄。
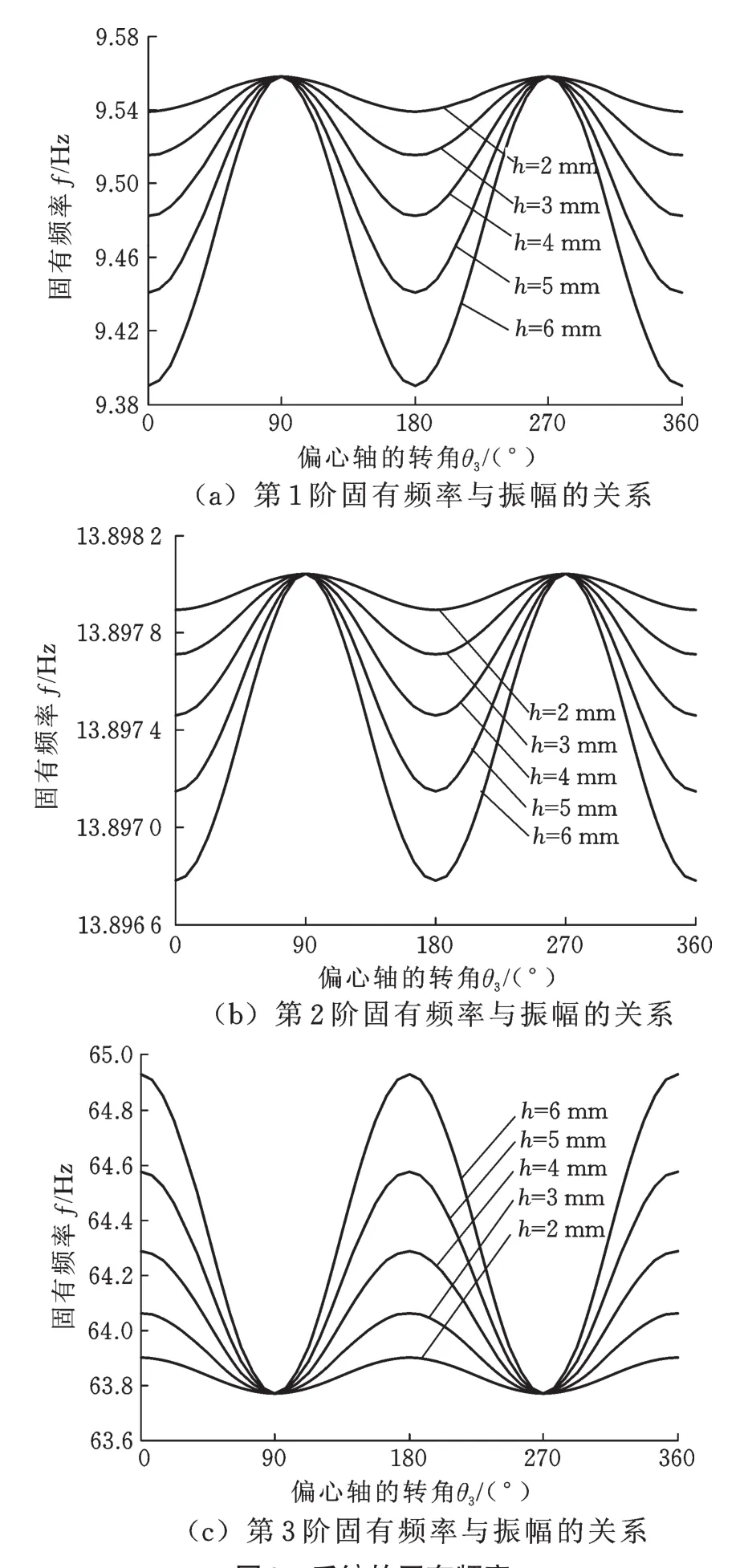
圖8 系統的固有頻率Fig.8 Natu ral frequency of the system
4.1.3 構件的剛度對固有頻率的影響
由圖10可以看出,偏心軸的剛度對系統的固有頻率改變較大,其他參數對固有頻率影響很小。
4.2 系統的振型
圖11給出了裝置的前3階振型,可以看出,系統的各階振型同固有頻率一樣,也是周期變化的,且在系統的傳動部分,振型變化較為劇烈。因此應增大傳動系統軸的剛度,減小傳動系統的轉動慣量,以提高系統固有頻率,降低傳動系統的波動。
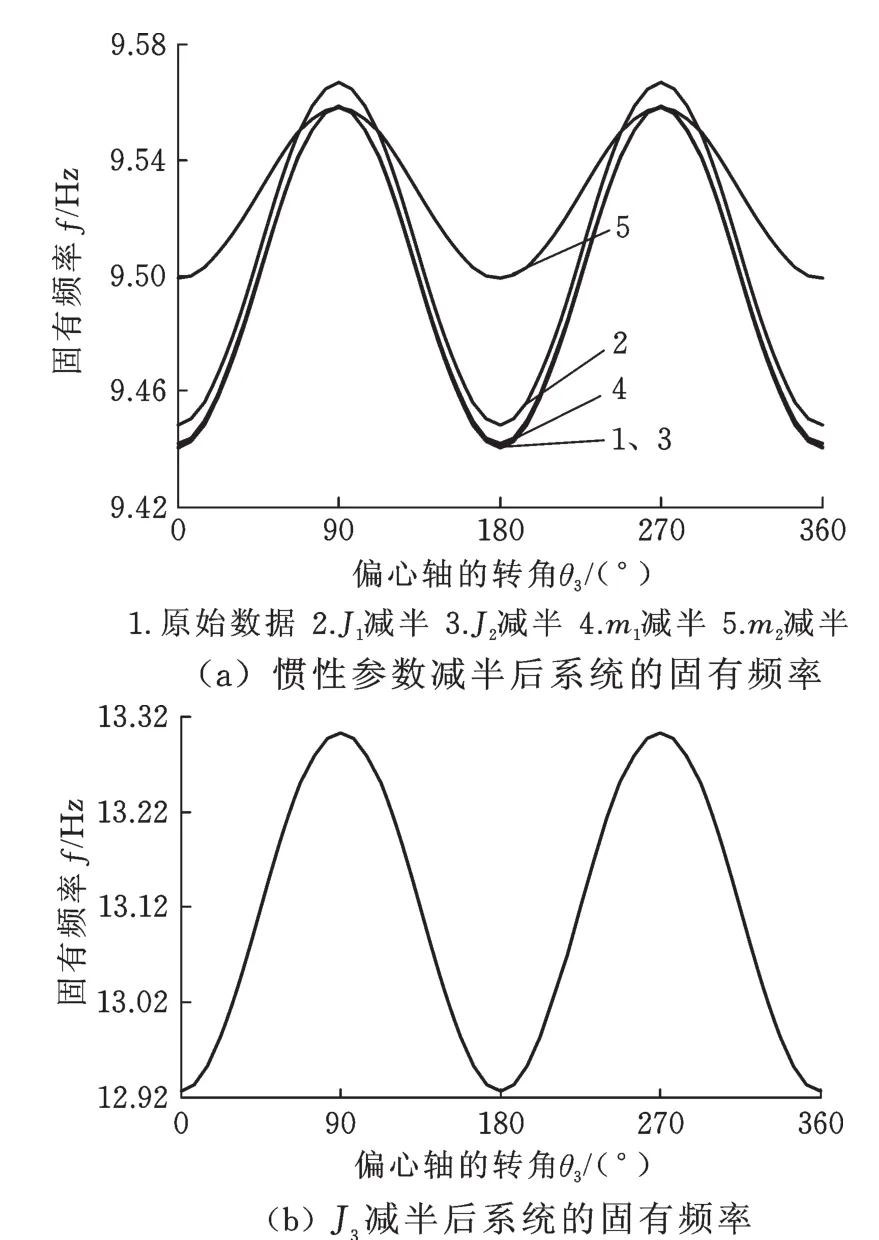
圖9 固有頻率與系統慣性參數的關系Fig.9 Relationship between natu ral frequency andinertia param eters of the system
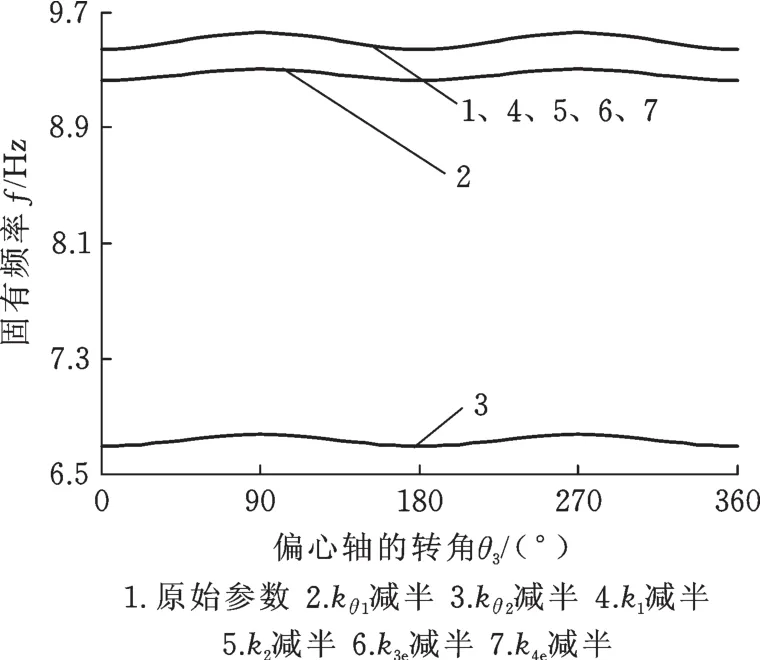
圖10 構件剛度減半后系統固有頻率Fig.10 Natural frequency of the system w ithcom ponent stiffness halved
5 結論
(1)設計出一種新型雙伺服電機驅動結晶器非正弦振動裝置,該裝置可以實現波形偏斜率和頻率的在線調節、振幅的停機可調。
(2)采用集中參數法建立了雙伺服電機驅動結晶器非正弦振動系統動力學模型及動力學方程。分析表明,固有頻率是周期時變參數,且不受結晶器振動頻率及波形偏斜率的影響,因此參數的選擇范圍擴大了,更有利于實現結晶器的最佳振動。
(3)偏心軸的轉角、慣性參數、剛度對系統的固有頻率影響較大,而其他參數影響較小;由振型顯示可得傳動部分的剛度對固有頻率影響較大。
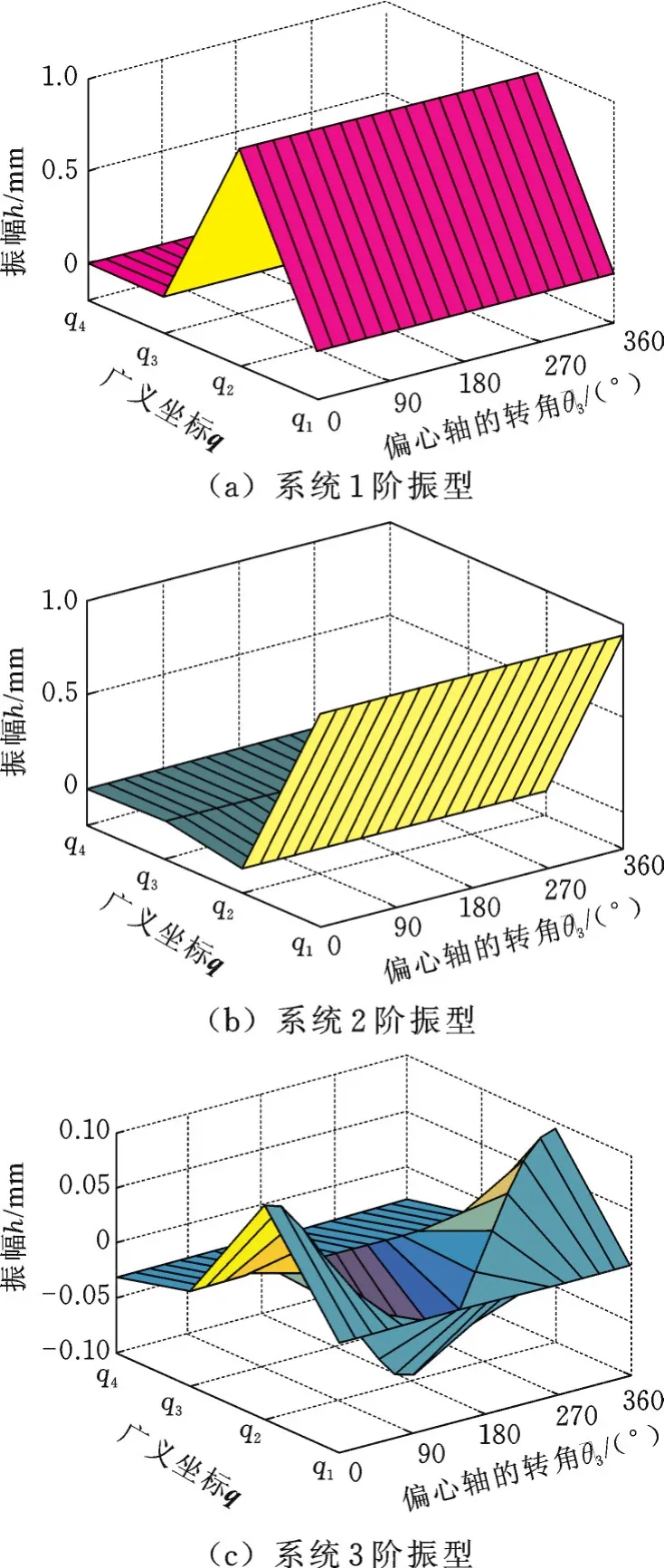
圖11 系統的振型Fig.11 System m ode shape

