復雜地質條件下砂巖滲透機理及模型探討

吳志剛 羅有權 張黎紅 陳行

摘要：為分析研究砂巖滲透性受各項地質因素影響的相互關系，對不同泥質含量和孔隙率的砂巖進行了不同應力環境下的三軸滲透試驗。試驗結果表明：滲透率隨著應力加載全過程呈先減小后增大的趨勢；體積變形擴容點與滲透率的突變點相對應，能準確反映滲透性的變化態勢；偏應力、泥質含量及孔隙率一定時，滲透率隨圍壓的增大呈負指數型減小；同等應力環境下，滲透率隨孔隙率與泥質含量比值的增大呈指數型增加。通過分析探討，建立了滲透性與圍壓、孔隙率、泥質含量相關的滲透經驗模型以及隨體積應變變化的擴展經驗模型，該模型能夠較為準確地反映復雜地質環境下砂巖滲透性的變化趨勢。

關鍵詞：砂巖；三軸；滲透；體變；孔隙率；泥質含量；模型

中圖分類號：TU45 文獻標志碼：A doi：10.3969/j.issn.1000-1379.2018.05.023

隨著現代水電、交通、礦山、油氣探井工程建設的蓬勃發展，其地下圍巖力學性質受到越來越多的關注和研究，其中砂巖是這些工程中最為常見的巖石之一，其滲透特性對工程的安全和穩定具有重要影響，一直是有關專家學者研究關注的焦點[1-2]。

姜振泉等[3]對砂巖、頁巖、黏土巖等軟、硬巖進行了不同壓力條件下的全應力一應變過程滲透對比試驗，認為巖石變形破壞過程中的滲透性主要取決于變形破壞的形式和特點；張守良等[4-5]研究了砂巖、泥巖等變形破壞過程中滲透率隨荷載的變化規律，并對其影響因素進行了探討，同時建立了滲透率與應力之間的關系式；張淵等[6]分析探討了溫度和孔隙壓力對細砂巖滲透率的影響規律，認為滲透率同時存在門檻值溫度和孔隙壓力門檻值；俞縉等[7]分析了全應力一應變過程中砂巖滲透率隨其脆性、延性變化的特點及滲透率一軸向應變和滲透率一體積應變之間的關聯性；王小江等[8]利用三軸耦合試驗機進行粗粒砂巖不同圍壓條件下變形破壞過程的滲流試驗，分析了粗粒砂巖變形破壞過程中滲透性變化規律和圍壓對于粗粒砂巖滲透性質的影響，推導了滲透系數與體積應變的關系。

砂巖的滲透性不僅受應力環境、粒度、溫度、孔隙壓力等因素的影響，而且與自身的物質成分含量相關，大量的試驗研究表明，泥質含量的多少也直接影響著砂巖的滲透性。在測井鉆探技術研究中，一些學者已對泥質含量對砂巖孔隙率、滲透率等的影響進行了相關研究。王連國等[9]應用突變學理論，研究了試驗全過程中滲透率與應力、應變之間的關系，建立了巖石滲透率與應力、應變關系的尖點突變模型。

上述研究大多僅針對砂巖滲透率與某一特定的影響因素，而關于復雜地質環境下的砂巖滲透率研究較少，如何預測復雜地質環境下砂巖滲透性的變化規律顯得尤為重要。因此，筆者嘗試利用不同泥質含量及孔隙率砂巖進行三軸全應力一應變滲透試驗，并根據試驗結果，得到復雜地質環境下砂巖的綜合滲透經驗模型。

1 試驗概況

1.1 試驗試件

試件取自某水電廠房地下工程埋深100～120m處，以中等粒徑顆粒為主，屬灰黑色沉積紋理中砂巖，通過D/Max-3B型X射線衍射儀分析得知砂巖的主要成分為石英、長石、方解石、泥質膠結物等，根據泥質膠結物含量將其分為4組，其平均泥質含量ω分別為4%、15%、24%、31%，通過試驗測定的對應孔隙率φ分別為17.8%、11.2%、7.8%、3.7%。將現場取回的巖芯按《工程巖體試驗方法標準》（GB/T 50266-2013）[10]通過鉆、切、磨的方法加工成50mm（直徑）×100mm（高）的標準圓柱體試件。

1.2 試驗方案

試驗共設σz=5、10、15、20MPa四個圍壓，施加圍壓后，對砂巖進行一次初始滲透測試，之后在應力加載過程中，用等加載應力差的測試方式，在峰前每隔10MPa進行一次測試，峰值應力處進行一次滲透測試，在峰后視情況進行2～3次測試。每次滲透測試時上下兩端初始壓差均為1MPa，圍壓加載速率為3MPa/min，荷載加載速率為60kN/min。

2 試驗結果及分析

2.1 應力一應變分析

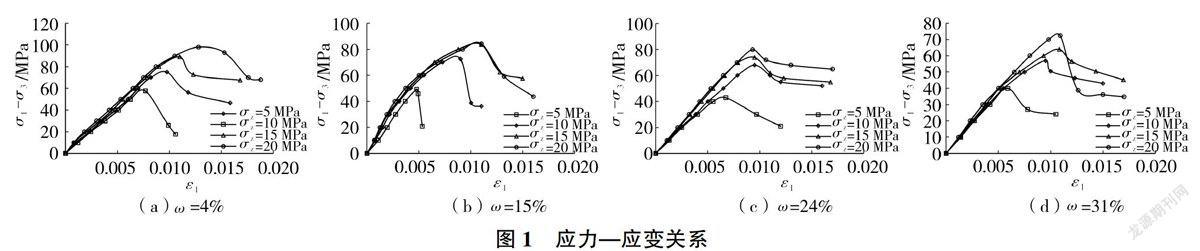
滲透試驗各組砂巖的應力一應變關系見圖1（σ1為第一主應力，σ3為第三主應力，σ1-σ3為偏應力，ε1為軸向應變）。從應力一應變曲線可以看出，砂巖在三維應力狀態下的變形過程包括壓密階段、彈性變形階段、塑性變形階段及峰后殘余階段。相同泥質含量下，隨著圍壓的升高，砂巖的變形能力逐漸增強，塑性變形特征更明顯，破壞時達到的軸向應變有逐漸增大的趨勢，而破壞方式逐漸由脆一延性向延性破壞轉變，并呈典型的剪切破壞特征。

2.2 滲透率一應變分析

為進一步分析砂巖滲透率與應變之間的關系，點繪了5MPa圍壓對應的各泥質含量下滲透率隨軸向應變及體積應變的演變曲線，見圖2（εv為體積應變、к為滲透率）。從圖2可以看出，滲透率隨軸向應變的增大，先略微減小并逐漸趨于動態平衡狀態，這一階段主要對應砂巖的壓密及彈性變形區，對應的體積應變逐漸增大，砂巖處于體積壓縮階段，該階段主要為巖石封閉應力調整。試件各項力學性質有所增強，即壓縮硬化過程，此時滲流通道主要為砂巖的原始微裂隙、微裂紋，而由于砂巖初期的壓密閉合作用使得滲透率相對于加載前略有減小，在彈性階段并沒有產生新的損傷，因此滲透率維持在某一相對恒定值；砂巖進入屈服階段后，滲透率逐漸增大，并在峰前快速增大，在此階段，新生裂紋逐漸產生并發展，水通過這些新生裂紋進行滲流，大量裂紋貫通，形成宏觀裂紋和裂隙，此時砂巖處于體積剪脹損傷狀態，因此滲透性會顯著增強；峰后殘余變形階段，滲透系數相對峰值附近有所減小，此階段砂巖處于軟化剪脹損傷狀態，巖石內部應力重新分布，產生的破裂面在荷載作用下又被重新壓密，且破壞時產生的碎屑和泥質顆粒會堵塞部分通道，同時由于峰后階段采取應變控制的方式，使得軸向應力出現松弛現象，裂紋擴展速度變緩，因此滲透率均出現一定降低。由上述分析可以看出，體積應變的發展演化過程反映了試件內部的硬軟化一損傷過程，體積變形擴容點與滲透率的突變點相對應，能準確反映滲透性的變化。

2.3 滲透率一圍壓分析

相同泥質含量及孔隙率下（以泥質含量4%為例），砂巖的滲透率隨圍壓的變化情況見圖3。由圖3可知，相同泥質含量及孔隙率的砂巖在同一加載偏應力下，圍壓越大，滲透率越小，隨著圍壓的升高，滲透率呈對數函數減小，表明滲透性因更大的側向約束力使得砂巖試件內部結構更加致密而逐漸減小。砂巖的初始滲透通道主要依靠原始微裂隙和微孔隙，但圍壓越大會使得內部顆粒更大程度上被擠壓密實，因此滲透率越小；應力加載過程中，由于存在更大側向約束力，使得試件內部的滲流通道發展更為緩慢，因此滲透率隨圍壓的增大而減小。

2.4 滲透率—泥質含量（孔隙率）分析

同等應力環境下，砂巖的滲透率隨泥質含量及孔隙率的變化情況見圖4（僅列出圍壓5MPa、偏應力0MPa以及圍壓15MPa、偏應力10MPa的情況進行說明）。可以看出，隨著泥質含量和孔隙率的增大，滲透率分別呈線性減小和增大，原因是泥質膠結物顆粒較細，與其他物質相互膠結形成的滲透通道更細小，泥質膠結物對滲流通道的阻塞作用越明顯，而砂巖內部顆粒間排列越緊密使得孔隙率越小，砂巖滲透率越小。

王小江等[8]在油氣測井技術研究中通過大量理論分析認為：處于同一層面（即所處應力環境基本一致）的砂巖，其滲透率隨孔隙率與泥質含量比值的增大呈冪函數遞增。借簽該研究經驗，可以得到本次試驗砂巖隨孔隙率與泥質含量比值的關系（以初始滲透率為例），見圖5。從圖5可以看到，本次試驗砂巖在同一圍壓下的初始滲透率K0與φ/ω之間成良好的對數函數關系（復相關系數均大于0.97），即式中：c、d為與圍壓相關的經驗常數。

3 復雜地質條件下砂巖滲透經驗模型

3.1 模型的建立與驗證

一般而言，圍巖應力的大小隨地層深度的增大而增大，從上述試驗研究結果可以看出，砂巖的滲透性不僅與孔隙率、泥質含量等相關，還與圍壓大小密切相關。因此，在前人研究的基礎上，認為砂巖的滲透率是這三者的函數，即

K =f（σz，φ，ω）（2）

由式（1）可知，同一圍壓下к0與φ/ω成良好的對數函數關系，而通過統計分析發現各圍壓下經驗系數c、d與圍壓存在圖6所示的函數關系。由圖6可以看出，c隨著圍壓的增大呈對數函數降低，而d隨圍壓升高呈線性減小，復相關系數均大于0.99，那么可以定義砂巖在各圍壓下的初始滲透率為式中：α、β、λ、η為與圍壓相關的經驗常數。

本滲透理論經驗模型不僅考慮了孔隙率、泥質含量對砂巖滲透性的影響，還將圍壓考慮在內，得到了復雜地質條件下砂巖的滲透經驗模型。采用式（3）可以預測各地層深度及對應泥質含量、孔隙率下砂巖的滲透率。以圍壓5MPa為例，圖7給出了本次試驗所測砂巖滲透率與理論經驗模型預測滲透率的對比情況。從圖7可以看到，理論預測值與試驗值相差較小，表明了本經驗模型具有一定的準確性和可靠性。

3.2 模型的擴展

在室內試驗應力加載過程中，隨著巖石的體積變化，其內部的孔隙率也會發生相應的變化，廣泛應用的Kozeny-Carman方程[11]從理論上說明了二者的關系。巖樣滲透率隨孔隙率變化關系為式中：kz為無量綱常數，取值約為5；∑為單位體積多孔介質內孔隙的表面積；Sp為孔隙介質單位孔隙體積的孔隙表面積。

根據孔隙率的定義可推導出試驗過程中孔隙率隨體積應變（忽略圍壓加載引起體積應變的微弱變化量）的變化存在如下關系：式中：φ0為初始孔隙率。

結合式（4）、式（5）可得

因ε<10%， （1+εv）3≈1+εv，故有

結合式（3）、式（7）可得：

式（8）即為考慮應力加載情況下砂巖的滲透率與含泥量、孔隙率、圍壓及體積應變的關系建立的復雜地質環境下砂巖試驗經驗擴展滲透模型。

由于破壞時產生的碎屑和泥質顆粒會堵塞部分通道，影響砂巖的滲透特性，因此式（8）只考慮破壞前的滲透變化性。以本文試驗砂巖數據為例進行驗證分析（以泥質含量為巧%、孔隙率為11.2%及圍壓為5MPa為例），見圖8。從圖8可以看到，理論值比試驗值稍小，但平均相對誤差不到15%，表明本理論模型能夠在一定程度上較為準確地預測應力加載下砂巖隨體積應變變化的趨勢。

4 結論

（1）體積應變擴容點與滲透率的轉折突變點相對應，體積應變能較為準確地反映滲透率的變化趨勢。

（2）加載偏應力、泥質含量以及孔隙率一定時，砂巖的滲透率隨圍壓的增大而減小；相同應力環境下，砂巖初始滲透率隨孔隙率與泥質含量比值的增大呈指數函數增大。

（3）通過試驗分析，建立了復雜地質條件下砂巖的經驗滲透模型，該模型能較好地預測各地層深度、泥質含量及孔隙率下砂巖的滲透率。

參考文獻：

[1]楊吉山，姚文藝，鄭明國，等.原狀砒砂巖坡面產流產沙規律試驗研究[J].人民黃河，2017，39（1）：98-102.

[2]張凌凱，張遠芳，劉亮.飽和砂礫土動孔壓發展規律試驗研究[J].人民黃河，2017，39（2）：136-139.

[3]姜振泉，季梁軍.巖石全應力—應變過程滲透性試驗研究[J].巖土工程學報，2001，23（2）：153-156.

[4]張守良，沈琛，鄧金根.巖石變形及破壞過程中滲透率變化規律的實驗研究[J].巖石力學與工程學報，2000，19（增刊1）：885-888.

[5]郭琴，張金功，王永詩，等.泥質巖和泥巖滲透率特征及其影響因素分析[J].蘭州大學學報（自然科學版），2008，44（增刊1）：46-48.

[6]張淵，趙陽升，萬志軍，等.不同溫度條件下孔隙壓力對長石細砂巖滲透率影響試驗研究[J].巖石力學與工程學報，2008，27（1）：53-58.

[7]俞縉，李宏，陳旭，等.滲透壓-應力耦合作用下砂巖滲透率與變形關聯性三軸試驗研究[J].巖石力學與工程學報，2013，32（6）：1203-1213.

[8]王小江，榮冠，周創兵.粗砂巖變形破壞過程中滲透性試驗研究[J].巖石力學與工程學報，2012，31（增刊1）：2940-2947.

[9]王連國，繆協興.巖石滲透率與應力、應變關系的尖點突變模型[J].巖石力學與工程學報.2005，24（23）：4210-4214.

[10]中華人民共和國建設部.工程巖體試驗方法標準：GB/T50266-2013[S].北京：中國計劃出版社，2013：19-24.

[11]盧平，沈兆武，朱貴旺，等.巖樣應力應變全程中的滲透性表征與試驗研究[J].中國科學技術大學學報，2002，32（6）：678-684.