基于高中數(shù)學(xué)核心素養(yǎng)的概念教學(xué)的研究

江蘇省張家港市崇真中學(xué) 白桂華

高中階段的數(shù)學(xué)知識相對難度比較大，學(xué)生們?nèi)绻胍獙W(xué)好數(shù)學(xué)這門學(xué)科，首先就必須將高中數(shù)學(xué)所涉及的各種概念知識牢記于心。為了讓學(xué)生們能夠更好地將這些抽象的概念知識銘記于心，教師們就需要基于高中數(shù)學(xué)核心素養(yǎng)，引導(dǎo)學(xué)生們重視概念知識的學(xué)習(xí)，并能夠運(yùn)用多種方式進(jìn)行記憶，提升學(xué)生數(shù)學(xué)水平。

一、基于核心素養(yǎng)，重視概念教學(xué)

高中數(shù)學(xué)這門學(xué)科相比于其他學(xué)科，本身難度就要更大，對學(xué)生們的記憶能力以及思維能力都有著很嚴(yán)格的要求，學(xué)生們在學(xué)習(xí)的過程中也比較容易喪失興趣，對于這門學(xué)科產(chǎn)生抵觸情緒，更不用說面對抽象的數(shù)學(xué)概念的學(xué)習(xí)，學(xué)生們更是抱著能避則避的態(tài)度。然而沒有良好的數(shù)學(xué)概念基礎(chǔ)，學(xué)生們在做題的時候就很難正確理解題目中所給出的各種條件，進(jìn)而不能夠順利推導(dǎo)出解題所必需的線索。我們在教學(xué)的時候應(yīng)當(dāng)從態(tài)度方面對學(xué)生們進(jìn)行糾正，讓學(xué)生們重視數(shù)學(xué)概念方面知識的學(xué)習(xí)，要求學(xué)生們從內(nèi)心深處認(rèn)識到數(shù)學(xué)概念的重要性。

在數(shù)學(xué)概念相關(guān)知識學(xué)習(xí)的過程中，要順應(yīng)新課改要求，從認(rèn)識、技能以及過程等三個方面入手，對學(xué)生們的數(shù)學(xué)思維進(jìn)行培養(yǎng)，要求學(xué)生們在做題的時候要仔細(xì)讀題，吃透題目中所給出的條件，按照題目中給出的條件，找尋對應(yīng)的數(shù)學(xué)概念，進(jìn)而探尋出出題人在題目中所埋設(shè)的隱藏信息，迅速完成解題。教師在組織學(xué)生們進(jìn)行高考復(fù)習(xí)的時候也需要強(qiáng)調(diào)概念知識的復(fù)習(xí)，在每一次復(fù)習(xí)中多對學(xué)生們進(jìn)行概念的考查，以此來幫助學(xué)生們深入理解。例如在講到函數(shù)定義域部分知識的時候，有例題：已知函數(shù)求函數(shù)定義域。在這個例題中，我們要考慮到二次根式以及分母這兩個因素，得到結(jié)果為

二、基于核心素養(yǎng)，激發(fā)學(xué)生思維

高中階段的數(shù)學(xué)知識已經(jīng)不僅僅考查學(xué)生們對于基礎(chǔ)數(shù)學(xué)知識的運(yùn)用能力了，而是對于學(xué)生們的理解能力和舉一反三能力有很高的要求，這就直接影響了學(xué)生們的學(xué)習(xí)。如果只是死記硬背書本上的數(shù)學(xué)概念，在實(shí)際做題的時候也完全不知從何下手。因此，教師在為學(xué)生們講解數(shù)學(xué)概念知識的時候，就要基于高中數(shù)學(xué)核心素養(yǎng)，讓學(xué)生們能夠真正地理解數(shù)學(xué)概念的內(nèi)涵以及意義。教師需要不斷激活學(xué)生們的思維，讓學(xué)生們保持靈活的頭腦，展開啟發(fā)式教學(xué)，通過向?qū)W生們拋出問題與學(xué)生們進(jìn)行思維上的溝通、交流，以此來確認(rèn)學(xué)生們真正理解數(shù)學(xué)概念。

很多數(shù)學(xué)概念的文字表達(dá)描述過于復(fù)雜，學(xué)生們即使能夠理解其對應(yīng)的性質(zhì)，在記憶數(shù)學(xué)概念的時候也很容易被搞暈。因此，針對這些內(nèi)涵相對豐富而且有著很強(qiáng)延展性的數(shù)學(xué)概念的教學(xué)的時候，教師就可以實(shí)行分層教學(xué)的方式，將描述比較冗長的概念分為多個段落或?qū)哟危瑸閷W(xué)生們逐層釋義講解，由淺入深地幫助學(xué)生進(jìn)行記憶，然后根據(jù)學(xué)生們平時的表現(xiàn)，按照學(xué)生們數(shù)學(xué)能力情況進(jìn)行提問，保證學(xué)生們能夠在課堂上積極思考，真正動腦想一想數(shù)學(xué)概念究竟討論了怎樣的問題，弄懂研究對象，這樣的教學(xué)方式可以很好地激活學(xué)生思維，還可以減輕學(xué)生們的學(xué)習(xí)負(fù)擔(dān)，構(gòu)建更為自由、活躍的數(shù)學(xué)課堂學(xué)習(xí)環(huán)境。

三、基于核心素養(yǎng)，結(jié)合引入技巧

為了幫助高中生們更好地理解數(shù)學(xué)概念，教師還可以嘗試引入法，如常用引入法、類比引入法以及發(fā)現(xiàn)引入法等，將數(shù)學(xué)概念與學(xué)生們所熟知的事物或者概念聯(lián)系到一起，通過引入法，學(xué)生們很容易展開聯(lián)想，繼而在學(xué)生們的腦海中構(gòu)建出具體的概念模型，將數(shù)學(xué)概念轉(zhuǎn)化為學(xué)生們自己腦海中的知識。例如在函數(shù)奇偶性的學(xué)習(xí)過程中，不必急于給出概念，馬上結(jié)合概念來練習(xí)題目，而是可以結(jié)合學(xué)生熟悉的二次函數(shù)、反比例函數(shù)的圖像特點(diǎn)來創(chuàng)設(shè)引入情景；

列表：你能從表格數(shù)據(jù)中觀察出什么一般規(guī)律嗎？

x…-2-2 0 1 2……4 1 0 1 4…… --1 無意義 1…

描點(diǎn)：你能從描出的這些點(diǎn)中觀察出什么一般規(guī)律嗎？

連線：上述規(guī)律可以用圖形來解釋嗎 ？

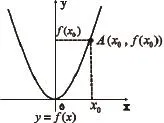
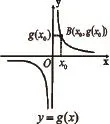
學(xué)生通過列表、描點(diǎn)、連線的步驟作出函數(shù)f（x）=x2，g（x）=的圖象，在這個過程中，列表體現(xiàn)出“數(shù)”的對稱性，描點(diǎn)體現(xiàn)出“點(diǎn)”的對稱性，最后連線成圖形則體現(xiàn)了“形”的對稱性，初步形成學(xué)生的認(rèn)知，為進(jìn)一步研究函數(shù)圖象的對稱性做好準(zhǔn)備。通過對熟悉實(shí)例的引入，學(xué)生在熟悉的環(huán)境中接受新知識，這樣學(xué)生就不會有陌生感、抗拒感，符合學(xué)生的認(rèn)知規(guī)律。

又如教師在為學(xué)生們講解集合的概念的時候，就可以利用事例引入法，嘗試著提出課堂互動任務(wù)，上課的班級中所在的所有男同學(xué)算作一個集合，班級中所有女同學(xué)又算作一個集合，全體同學(xué)也能夠算作一個集合，通過引入學(xué)生們身邊的事例，學(xué)生們對于集合的概念以及相關(guān)的交集、并集以及補(bǔ)集等概念也會有具體的理解。

比如在學(xué)習(xí)拋物線這部分知識的時候，教師就可以采取類比引入法，引入學(xué)生們熟知的二次函數(shù)以及橢圓、雙曲線的概念幫助學(xué)生們進(jìn)行理解，引導(dǎo)學(xué)生們找出這些概念之間的異同點(diǎn)，在引入類比事物的過程中使得學(xué)生們很好地區(qū)分相似的概念之間的特征，防止學(xué)生們混淆相似概念。而發(fā)現(xiàn)引用法往往應(yīng)用于復(fù)習(xí)階段，教師們從原有的概念知識入手，為學(xué)生們引入難度更大的問題，讓學(xué)生們不斷發(fā)現(xiàn)曾經(jīng)學(xué)習(xí)的概念并不能滿足于解題需求，從而修正概念，完善自身學(xué)習(xí)儲備。

總而言之，在高中數(shù)學(xué)學(xué)習(xí)過程中，數(shù)學(xué)概念的學(xué)習(xí)十分重要，學(xué)生們只有牢記相關(guān)數(shù)學(xué)概念，才能夠在眾多混淆條件中精確找出關(guān)鍵所在，完成解題，這就要求教師們在高中數(shù)學(xué)課堂上不僅僅要幫助學(xué)生們養(yǎng)成良好的學(xué)習(xí)習(xí)慣以及較強(qiáng)的數(shù)學(xué)功底，教師們還需要順應(yīng)高中數(shù)學(xué)核心素養(yǎng)，以此為教學(xué)根據(jù)來展開概念教學(xué)，嘗試多種教學(xué)方法，優(yōu)化課堂教學(xué)效果，幫助學(xué)生們牢記數(shù)學(xué)概念。