在建構數學問題情境中培育學生數學核心素養

江蘇省宜興市官林實驗小學教育集團 郭劍峰

一、要善于緊抓學生的心理需求

著名特級教師于漪曾說過：“課的第一錘要敲在學生的心靈上，激發起他們思維的火花，或像磁石一樣把學生牢牢地吸引住。”一節課的開始是否能很快抓住學生的心，對一節課的成敗非常關鍵。一上課，學生其實在生理和心理上都沒有做好學習的準備，甚至還停留在課間的十分鐘，這時更需要教師精心設計問題情境，讓學生不經意間掉進教師設置的“陷阱”，從而激發他們的學習興趣、喚醒思維，達到最佳學習狀態。

如在學習復式統計表前，做個搶答游戲：

觀察四張單式統計表搶答：

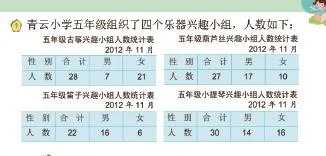
1.五年級葫蘆絲興趣小組有幾名男生？2.五年級笛子興趣小組男生多還是女生多？3.五年級哪個小組人數最多？4.五年級四個興趣小組一共有多少人？

搶答過程中學生發現，1、2兩題回答很快；3、4兩題回答速度明顯慢了很多，因為1、2兩題的答案在同一張統計表中，3、4兩題要整合四張表的信息，信息分散，不易迅速作答，所以學生在心理上就有把四張表的信息整合在一張表上的需求，也就有了學習復式統計表的需求。筆者用搶答游戲的方式，結合學生實際情況，創設問題情境，喚起學生的注意力，激發學生的學習需求，使學生主動、積極地投入到學習過程中。

二、要直擊學生的興趣愛好

托爾斯泰說過：“成功的教學所需要的不是強制，而是激發學生的興趣。”可見興趣對數學教學的成功起著定向作用，數學教學上的成就很大程度取決于學生對數學課的興趣是否保持和發展。只有當學生對問題有了強烈的興趣，才可能對問題大膽地去探究。學生能否大膽思考，善于思考，決定著學生對知識的牢固掌握和靈活運用程度。從學生興趣出發，創設問題情境，能促使學生掌握和運用知識，促進創新思維能力的形成和發展，從而為學習更高層次的知識奠定堅實的基礎。

例如在小數加、減法綜合練習時出示：3.86+2.75+（ ）。

師：看著題，教師覺得計算很有難度，你能在括號里填寫一個小數，使計算簡單些嗎？

求變、求簡正是學生的興趣所在，一下子思維活躍起來：“0.14、0.25”“1.14、2.14、3.14……”“1.25、2.25……”“湊成整數就行了。”學生在教師創設的情境引領下，體驗了根據數的特點合理簡便的過程，訓練了學生發散、有序、創新的思維，讓不同層次的學生實現了思維的拔節生長，發展了學生的數學素養。

三、要緊抓學生的最近發展區

維果斯基的“最近發展區理論”認為學生的發展有兩種水平：一種是學生的現有水平，指獨立活動時所能達到的解決問題的水平；另一種是學生可能的發展水平，也就是通過教學所獲得的潛力。兩者之間的差異就是最近發展區。教學應著眼于學生的最近發展區，為學生提供帶有難度的內容，調動學生的積極性，發揮其潛能，超越其最近發展區而達到下一發展階段的水平，然后在此基礎上進行下一個發展區的發展。

出示紙條2：

問：陰影部分可以用哪個分數表示？為什么？折一折。

出示紙條3：

問：陰影部分可以用哪個分數表示？為什么？折一折。

四、要在學生的“整體生長”處設疑

“整體生長”是基于“聯系的觀點”，這里的聯系不僅指數學與外部世界的聯系，也指不同數學概念、不同數學結論乃至不同數學理論之間的聯系。學生需要在認識、理解知識的本質及相互間的聯系的基礎上，形成良好的認識結構，優化數學在大腦中的組織形式，使學生的思維全面、靈活、深入，從而提高數學素養。

例如異分母分數加減法的教學中，教師出示：59+48=107，要探索的、有價值的問題情境，學生探究興趣也被充分調動起來，從而給思維以動力，自然就積極主動地投入到學習新知的過程中去了。可見，精心設計的問題情境，是促使學生建構良好認知結構的推動力，是激發學生探究興趣的重要措施，也是生成智慧的前提條件。

這些數的計算有什么相同點呢？學生通過觀察、比較、分析、歸納出整數、小數、分數的計算實則都是相同的幾個計數單位的加或減。

教師從知識整體出發，用聯系的觀點指導教學，在知識的連接處，在知識的從屬、對立、統一關系中，采用整體教學手段，把合理的知識結構及時呈現給學生，幫助學生理清各部分知識的脈絡及其在知識塊中的地位和作用，把大綱中“學會”這一目標具體化、系統化，使學生所學的知識不是幾個孤立的點，而是前后響應、渾然一體的有機整體，從而促使學生形成良好的認識結構，逐步具有“從整體看事物”的數學思想，培養有條理地思考和處理問題的能力。

學生的數學素養不是先天所具有的，也不是教師直接給予的，而是借助具體的問題情境，在問題的實踐中逐步培養出來的。因此，我們要創設切合實際的問題情境，給學生一些權利，讓他們自己去選擇。