單調約束的TSK模糊系統模型*

曹 雅，鄧趙紅，王士同

江南大學 數字媒體學院，江蘇 無錫 214122

1 引言

現實生活中存在著大量的有序分類問題，例如對學生學習成績的評定可分為優、良、中、差；地震對房屋造成的傷害程度分為輕微、中等、嚴重；制作衣服的材料和工藝決定了衣服的質量有好有壞，還有諸如對風險用戶等級的評定及決定處理不同事情的先后次序等問題。很明顯，在這些情況中，類標簽存在著有序關系。這些年，隨著對分類任務的研究，一般的分類問題已經取得了較好的分類準確率，但是這些任務中很少考慮序的關系，因此可能得到不一致的決策規則，這就需要研究者深入研究類標簽之間的順序關系。

單調分類問題一般是具有單調約束的有序分類問題，即屬性值與類標簽是有序的并且在它們之前存在單調關系。當一個對象的所有條件屬性上的取值都不比另一個對象差時，它的決策也不會比另一個對象的決策差，這就是單調分類任務[1-2]。在單調分類問題中，單調約束先驗知識的發現對分類器的改進非常重要，但傳統的智能算法未考慮過此類問題。因此，建立合適的數學模型充分利用數據中存在的單調約束知識，對單調分類領域的應用會有很大的幫助。此類問題目前在機器學習、數據挖掘等人工智能的各領域越來越引起人們的重視[3-4]。

眾所周知，模糊系統可以被應用于多種智能信息處理任務中，如聚類、回歸以及分類[5-7]。與大多數現有的智能模型相比，模糊系統在解釋性[8-9]和建模的不確定性方面具有獨特優勢。模糊系統已經被應用在工業過程控制、醫學診斷、圖像處理、機器人控制、財務預測、復雜系統控制等一系列的任務中，具有廣泛的應用價值[8-13]。TSK模糊系統是最流行的模糊系統模型之一。由于其簡單性、有效性和較好的彈性，得到了廣泛的研究，目前已提出了多種各具特色的構建算法，例如：大規模數據TSK模糊系統建模[10]、2型TSK模糊系統建模[14-16]和遷移學習建模[17]。與上述TSK模糊系統在回歸應用方面已有的較多研究成果相比，TSK模糊系統用于分類方面的研究相對較少。代表性的工作有：Jiang等人在文獻[18]中提出了一種新穎的TSK模糊分類器TSK-FC，它的目標函數是通過采用大間隔和最小化結構風險策略構建，把TSK-FC訓練等價地轉化為一個經典凸QP問題。文獻[19]提出了一種極大極小概率TSK模糊系統分類器，通過引入極大極小概率決策技術來訓練模糊系統的分類任務。對于該分類器，正確分類的下界可以呈現給用戶用來描述所訓練的模糊分類器的可靠性。所得的分類器同時具有繼承于模糊系統的較高可解釋性和基于最小最大概率學習策略的模型的良好可靠性。文獻[20]提出了一個深度TSK模糊分類器，它是由基本的TSK模糊系統構建單元組成，并以層疊的方式構建深度推理模型，模型的每一個基本構建單元通過最少學習機器學習，此分類器可以很好地應用在大規模的數據集中。

目前，現有的TSK模糊系統分類技術在單調分類問題上的研究仍然比較缺乏，已有的TSK模糊系統直接用于解決單調分類問題還不夠理想。針對單調分類任務的特點，研究相應的既具有傳統模糊分類器優點又能適應單調分類任務的TSK模糊分類器是非常必要的。

基于上述分析，本文提出了一種新的單調TSK模糊系統分類器（MC-TSK）。該模型添加了關于單調性的先驗知識，將單調約束施加在原始的TSK模型上。MC-TSK的數學模型是一個二次規劃問題，其中分類誤差與單調性均被考慮在內。不同于其他已存在的單調分類方法，MC-TSK不要求特征與決策屬性之前的單調關系是一致的，這就意味著不需要進行相關的數據預處理還可以避免一些信息的丟失。對于提出的新方法，在多組單調分類數據上進行了性能評估，實驗分析表明所提出的方法要優于傳統的TSK模糊系統分類方法和一些其他經典類型分類方法。

本文組織結構如下：第2章介紹了單調分類方面的一些概念以及TSK模糊系統的相關知識。第3章介紹了二分類單調TSK模糊系統的建模過程，并將其擴展到多分類任務中。第4章通過一些對比實驗研究評估所提方法的性能，并對實驗結果進行分析。第5章對本文進行總結以及展望。

2 相關工作

2.1 單調分類

假設U={x1,x2,…,xn}是對象的集合，A是用來描述對象的特征集，D是樣本的決策屬性代表分類問題的類標簽。樣本xi就屬性a∈A或者D的值分別被表示為v(xi,a)或者v(xj,a)。樣本中依據屬性a或者D之間的有序關系被表示為≤或者≥，那么可以說xj不比xi更差當且僅當v(xi,a)≤v(xj,a)或者v(xi,D)≤v(xj,D)，可分別表示為xi≤axj和xi≤Dxj。相應地，也可以定義為xi≥axj和xi≥Dxj。給定B?A，若有v(xi,B)=v(xj,B)，那么對于 ?a∈B，有v(xi,a)=v(xj,a)。

定義1給定一個特征a，讓B=A-{a}。對于?xi,xj∈U，在限制v(xi,B)=v(xj,B)下，當v(xi,a)≥v(xj,a)時有v(xi,D)≥v(xj,D)，或者當v(xi,a)≤v(xj,a)時有v(xi,D)≤v(xj,D)，說明決策屬性D關于屬性a是單調遞增的；否則當v(xi,a)≥v(xj,a)時有v(xi,D)≤v(xj,D)或者當v(xi,a)≤v(xj,a)時有v(xi,D)≥v(xj,D)，說明決策屬性D關于屬性a是單調遞減的。

也就是說，對于單調遞增的情況，如果一個樣本點的屬性值要高于另一個樣本點的屬性值，那么它的輸出值也會相應大于另一個樣本的輸出值，即存在一個在輸入與輸出變量之間的單調關系，增加輸入變量的值那么輸出變量的值也很有可能會增加。在現實生活中存在著很多單調分類問題，例如，根據學生成績進行獎學金的評定，成績越好的學生獲得的獎學金就越多；雇主選擇雇員時根據應聘者的學歷水平和工作經驗進行打分，學歷水平越高、工作經驗越豐富，那么打分就越高。

2.2 TSK模糊系統分類器

TSK模糊系統是最廣泛應用的模糊系統模型，本文選取了簡潔而又高效的0階TSK作為研究對象，那么基于0階TSK模糊系統的二分類方法簡介如下。

0階TSK模糊系統包含一個規則庫，其第k個模糊規則的表示形式如下[24]：

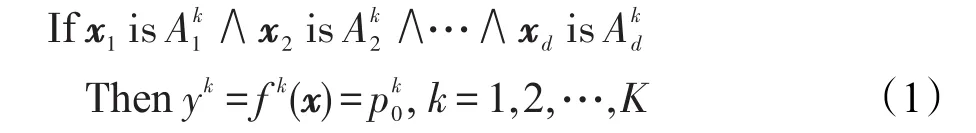
其中，If部分為規則前件，Then部分為規則后件。xj(j=1,2,…,d)表示第j維的輸入向量，yk表示輸出變量，每條規則把輸入空間的模糊集Ak?Rd映射到輸出空間的模糊集yk，這里表示輸入向量x第d維所對應的第k條規則的模糊子集，K是模糊規則個數，∧為模糊合取操作。如果采用乘法合取算子、加法析取算子和組合算子，以及對輸出采用重心法去模糊化等操作，最終TSK模糊系統的實值輸出可表示為：

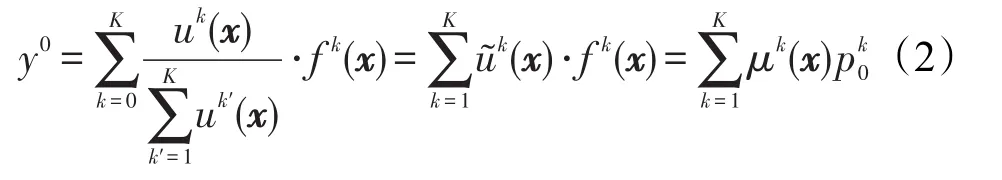
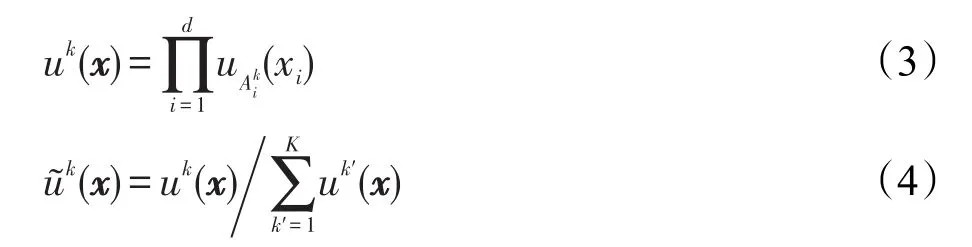
通常采用高斯隸屬度函數作為隸屬度函數，該隸屬度函數可表示為：

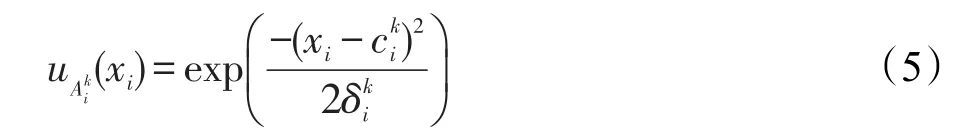
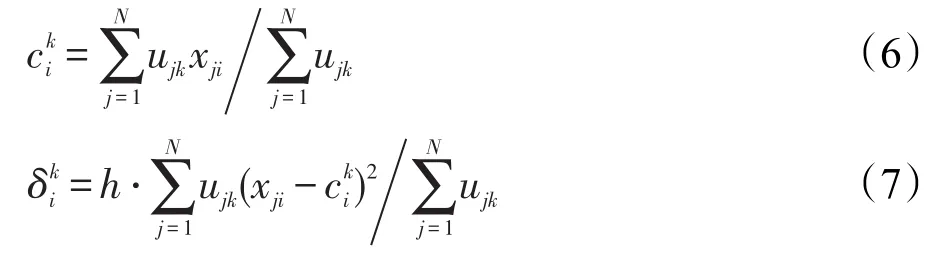
其中，ujm表示由FCM得到的第j個輸入數據xj=(xj1,xj2,…,xjd)T輸入第m類（即第m條規則）的隸屬度。這里，h是人工可調的尺度參數。

當TSK模糊模型的前件參數確定后，可令

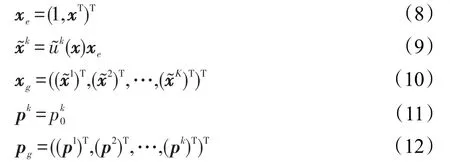
那么式（2）可以表示為下面的線性規劃問題[22]：

基于經典的TSK模糊系統，TSK模糊系統用于二分類時常采用如下的決策函數：

為了對該二分類器進行有效的訓練，常需構造有效的優化目標函數對參數進行優化和學習。例如，文獻[18]中給出了一種基于間隔最大化的優化準則。這里簡單描述如下：以分類為目的，給定訓練數據集中的任意樣本點{xi,yi}，最大化邊界問題就是最大化下面的判別函數：

式（15）的準則可被重寫為：

其中，ε表示間隔。由于上述約束條件不可能適應所有的數據點xgi(i=1,2,…,N)，可以通過引入松弛變量ξi≥0(i=1,2,…,N)得到下面的約束條件：

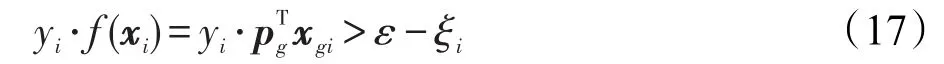
基于式（16）和式（17），可見上述的分類機制和著名的支持向量機（support vector machine，SVM）有很大的相似之處，即都是基于最大化間隔來優化分類器。進一步引入正則化項，可得到如下最小化結構風險的優化目標函數：

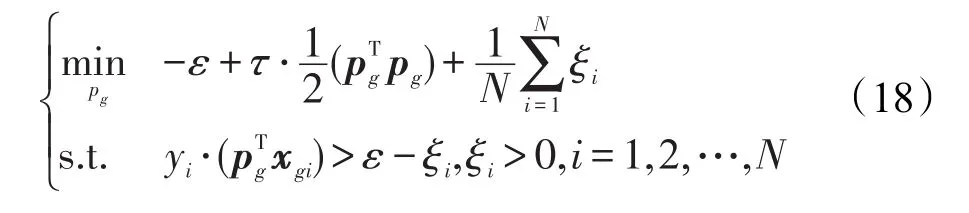
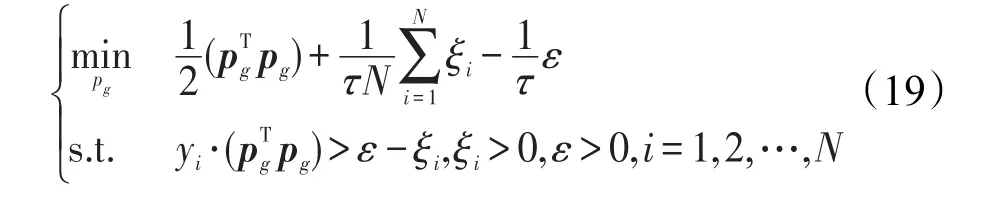
3 單調TSK模糊系統模型

基于2.2節提出的二分類0階TSK模糊系統分類器，本文針對單調分類場景提出一種單調TSK模糊系統分類器。

3.1 二分類TSK模糊系統

（1）優化目標函數的構建

由2.2節知，對于0階TSK模糊系統模型用于二分類，其輸出為為模糊規則數。當解決基于MC-TSK的單調分類問題時，若對于特定特征需要增加單調性，則關于特征的決策屬性的偏導數被限制為正。反之，對于要求降低單調性的特征的偏導數被認為是負的。不需要特征和決策屬性之間的所有單調關系是一致的，也就是說，一些單調關系可以遞增，一些可以遞減。

通過限制偏導數的符號，可以在單調問題中獲得r對單調約束，其中r是相對于決策屬性單調增加或減少的特征的總數，并且有1≤r≤n，n是特征總數[23]。將這些約束添加到TSK模糊系統模型中即可得到單調TSK模糊系統模型。

增加單調約束關系到TSK模糊系統模型中，可以構建如下的單調TSK模糊系統模型：

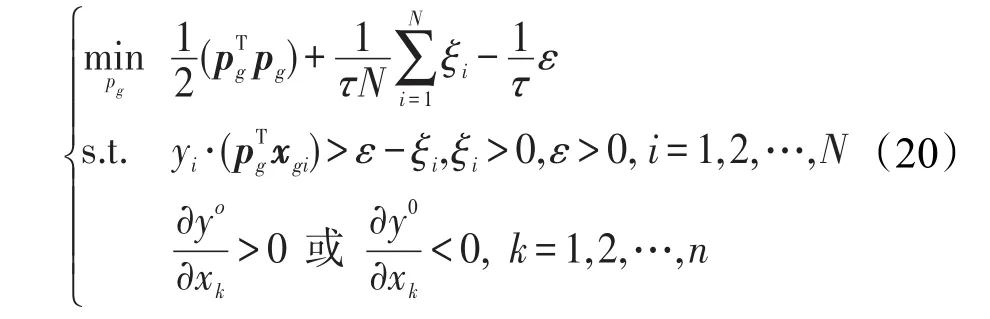
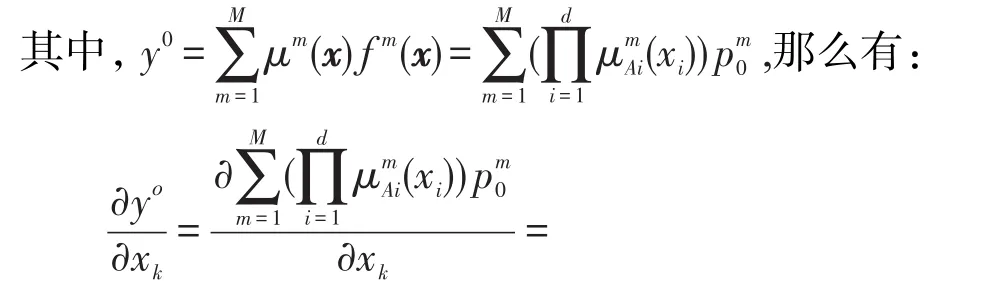
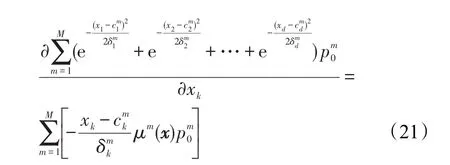
如果決策屬性關于特征xk是單調遞增的，那么關于xk的決策屬性的偏導數就是正的，此時有

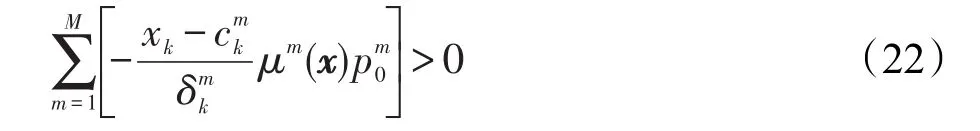
類似的，如果決策屬性關于特征xk是單調遞減的，那么關于xk的決策屬性的偏導數就是負的，此時有

其中，M是模糊規則數，由2.2節知對于所有的k=1,2,…,n都成立。那么式（22）與式（23）可分別簡化為：

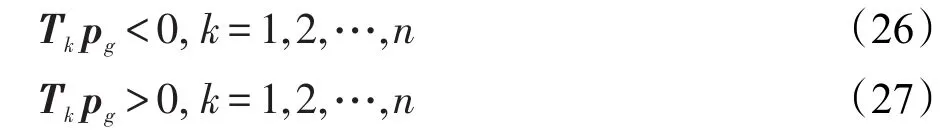
（2）優化求解

基于優化理論，對于單調關系是遞增的情況，式（20）的拉格朗日函數可表示為：

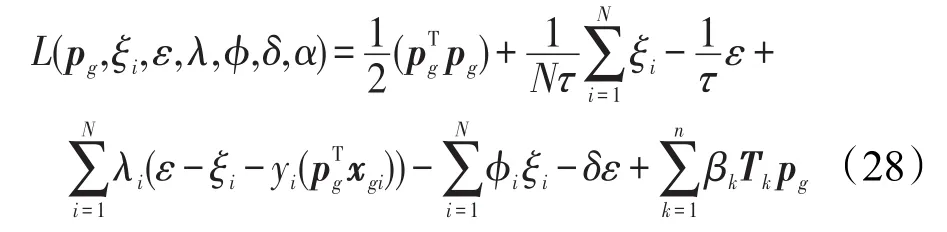
通過拉格朗日函數對pg,ξi,ε取極值，得到：

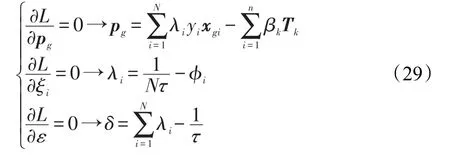
將式（29）帶入式（28）中，可得到原問題的對偶問題：

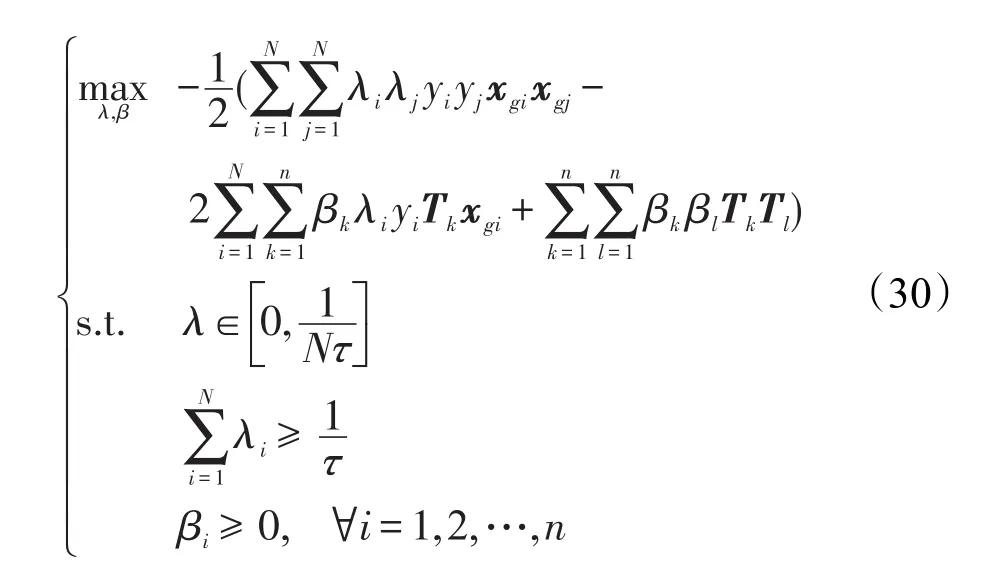
通過求解對偶問題的最優解λ?和β?，根據式（29）即可得原問題的最優解

類似的，對于單調關系是遞減的情況，通過求解可得原問題的對偶問題為：

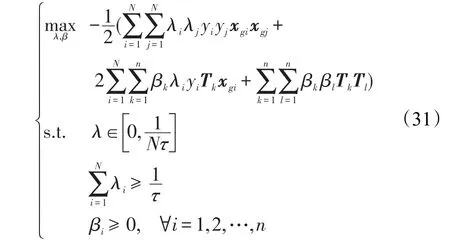
（3）Tikhonov正則化項

對于單調遞增的情況，式（31）可表示成如下的矩陣形式：

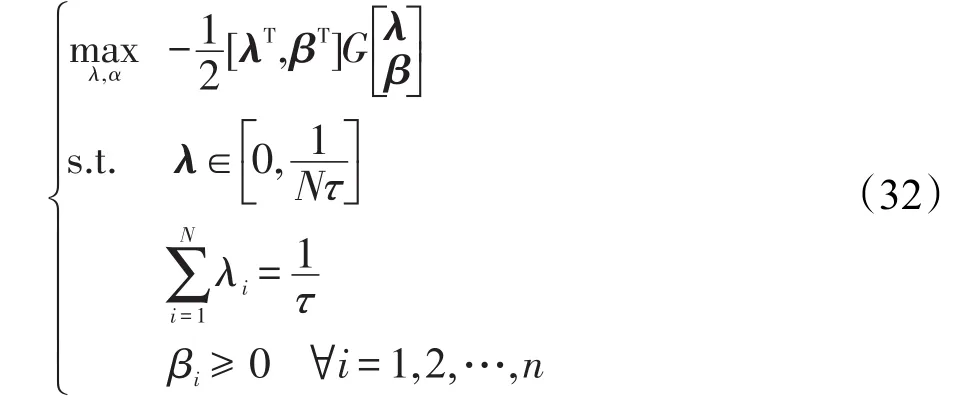
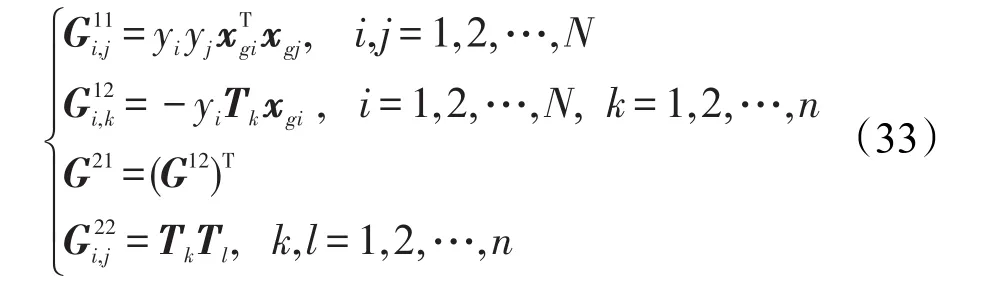
如果G矩陣是半正定的，優化目標具有全局最優解；如果是正定的，那么最優解是唯一的全局最優解。

為了避免問題求解時出現欠正定情況，可在目標函數中引入Tikhonov正則化項，此時優化目標函數可修正為：

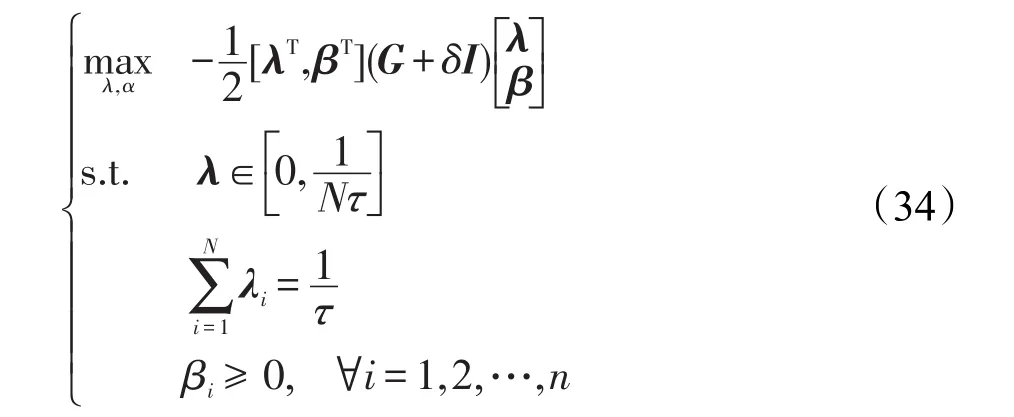
其中I是單位矩陣，如果δ選取合適的話，那么式（34）中的二次規劃問題將是一個凸二次規劃問題并且具有全局最優解。通過使用不同的數據集對式（32）的單調TSK模糊系統模型進行驗證，結果表明，二次規劃問題可能是一個不適定問題，此時矩陣G包含一個非常小的負特征值。針對此，本文將懲罰項δ設置成G的最小負特征值的絕對值的兩倍。按此方法，式（32）中的二次規劃問題將能保證是正定的。

類似的，對于單調關系是遞減的情況，在目標函數中引入Tikhonov正則化項，此時優化目標函數同式（34），其中Hessian矩陣中4個子矩陣分別為：

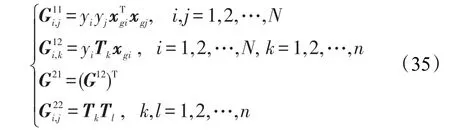
與式（33）不同在于G12與G21的符號與之相反。

3.2 多分類單調TSK模糊系統

為了保持數據集使用過程中的單調性，在對單調多分類數據集進行處理時，采用“一對一”的方法。本文采用的策略是每次從數據集的k個類別中挑選出兩個不同類別，對這兩類數據進行訓練從而構造二類分類器，并將類標簽中大的標簽映射為+1，類標簽小的映射為 -1，這樣共可構造出k(k-1)/2個單調分類器。在對未知樣本進行測試時，“一對一”方法使用的決策機制是投票選舉法。k(k-1)/2個分類器分別對未知樣本做出決策，再將測試后的類標簽反映射為原數據集中對應類標簽，并將最終所判斷的類別投票數增加1，得票最多的類別即為未知樣本所屬的類。

3.3 單調TSK模糊系統學習算法

基于上文所提出的單調TSK模糊系統學習算法的原理與模型的構造過程，給出其詳細的算法描述。

算法1單調TSK模糊系統算法

階段1數據處理階段

步驟1設置模糊系統的規則數M，懲罰項系數M∈{10,20,30,40,50,60,70,80,90,100}以及人工調節的標量參數h；選取用于單調分類場景的數據集。

階段2構建單調TSK模糊系統模型

步驟2設置單調約束對的個數Ms；構建式（19）所示的二分類0階TSK模糊系統模型，利用交叉驗證法得到當前模型的測試數據集。

步驟3在TSK模糊系統模型上添加單調約束，構建式（20）所示的單調TSK模糊系統模型的目標函數。

步驟4對式（20）所示的目標函數進行優化求解得到原問題的對偶問題。

步驟5在優化后的目標函數中引入Tikhonov正則化項，將目標函數修正為式（34）得到單調二分類TSK模糊系統模型。

階段3構建單調多分類TSK模糊系統模型

步驟6用“一對一”的投票法將單調二分類TSK模糊系統模型改進為單調多分類TSK模糊系統模型，算法終止。

4 實驗研究

4.1 實驗設計

為了確保實驗的公正性，本文所有實驗的實驗環境為：MATLAB編程環境，電腦配置為Windows系統，3.30 GHz的Intel?CoreTMi5-4590 CPU，16 GB內存。

4.1.1 實驗數據集

實驗選取了UCI數據庫中具有一定單調性的8個真實數據集，數據集的細節如表1所示。

4.1.2 參數設計

本文算法所涉及的參數會影響模型的性能。針對此本文對于懲罰項系數τ與人工調節的標量h等參數，采用了網格搜索和交叉驗證結合的方法進行了尋優。過程如下：首先對于每個待優化的參數，給定一個尋優范圍（具體范圍見表2），然后利用交叉驗證的方式來計算特定參數下的所訓練模型的性能，最終把取得最優性能的參數作為最終的參數。特別地，為了便于找到較優的參數，表2在一個較大的范圍內設置了參數尋優范圍。本文實驗中采用了5倍的交叉驗證法，即把數據集劃分為5份，每次選取1份數據作為測試集，其余4份作為訓練集。對于本文實驗所采用的比較算法和所涉及的相應超參數的搜索網格如表2所示。

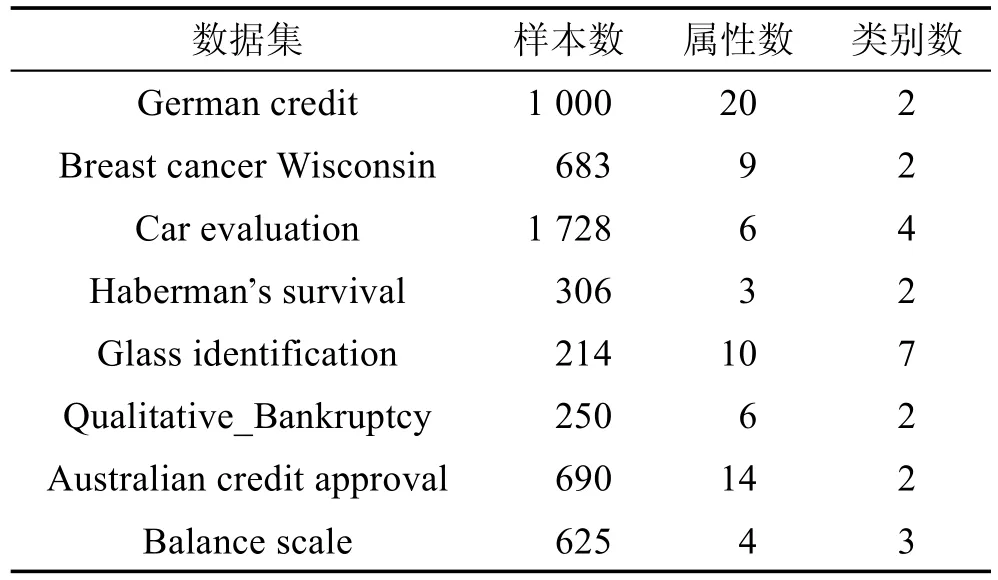
Table 1 Description of dataset表1 數據集描述

4.2 實驗分析

本文用到的對比算法有傳統的TSK模糊系統[24]，正則化單調模糊SVM（regularized monotonic fuzzy support vector machine，RMCFSVM）[25]、SVM[26-28]、FSFCSVM（fuzzy system learned through fuzzy clustering and support vector machine）[29]以及FSC-0-L2-TSK-FS（fuzzy subspace clustering based zero-order L2-norm TSK fuzzy system）[30]。各個算法的分類精度如表3所示。

通過觀察表3可以看出：

本次實驗選取了8個單調數據集，均在本文提出的算法中獲得最優的分類性能，在其他單調方法中獲得較好的分類性能，并且幾個數據集均有較好的穩定性。

對于不同的單調數據集，對TSK模糊系統分類器添加了單調約束后其分類性能要明顯優于沒有添加單調性約束的分類器。本文應用的對比算法中的另一個單調方法RMC-FSVM一般情況下也要優于其他非單調方法，但是仍次于本文提出的優化方法MC-TSK。對于數據集Qualitative_Bankruptcy，由于其數據屬性較少，單調性也較明顯，此時單調TSK模糊系統準確率可達到100%，也是這8個分類器中分類性能最好的，同樣穩定性也是最優的。

對于同一個數據集，單調多分類TSK模糊系統分類器得到的準確率明顯高于普通的TSK模糊系統分類器，一般情況下也優于其他幾個分類器。例如對于數據集Car evaluation，在MC-TSK上獲得的準確率比在普通的TSK以及FS-FCSVM上獲得的準確率高達20%多，比在其他分類器上高達10%，可見改進后的算法分類性能獲得了明顯提升。

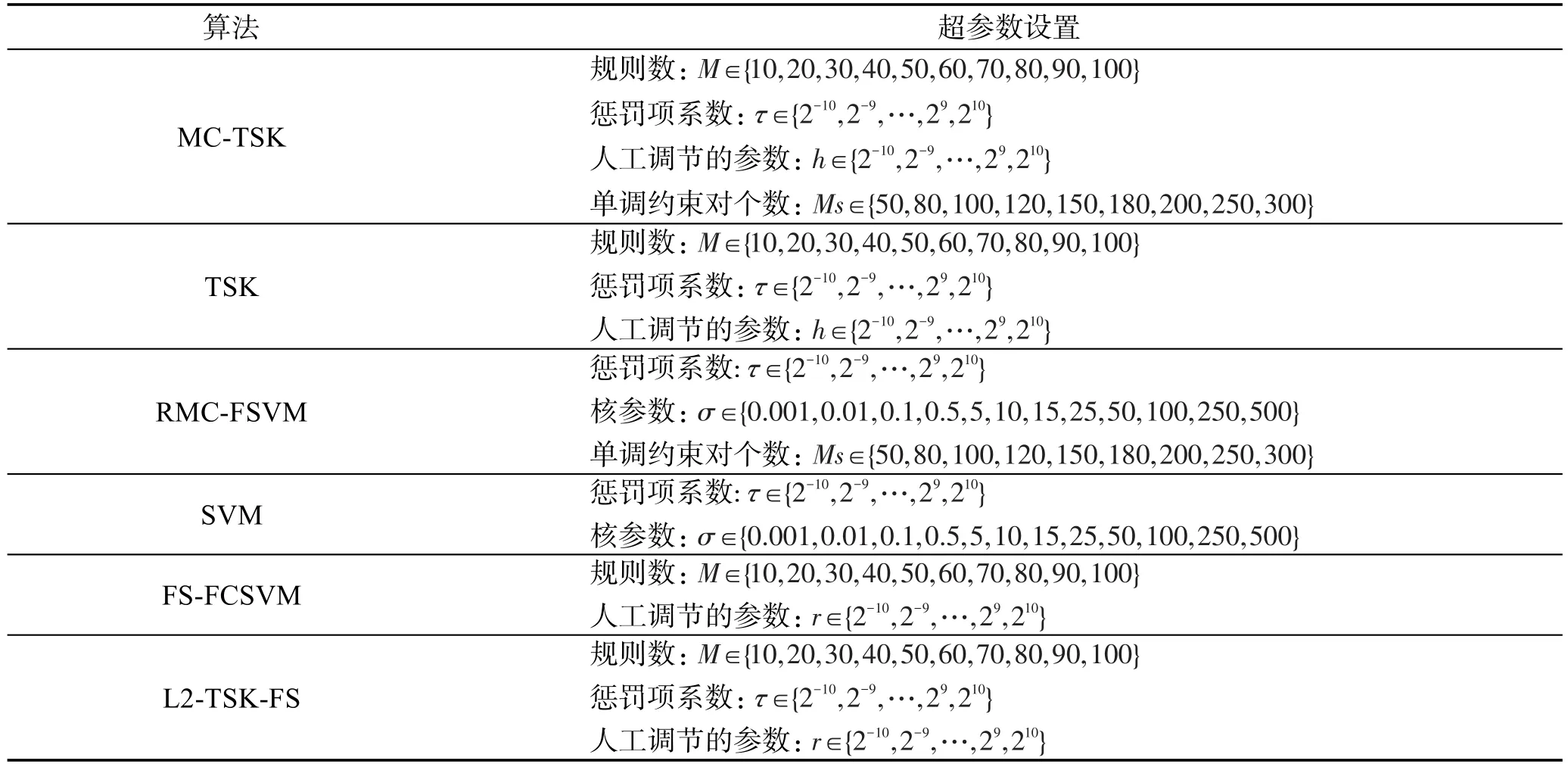
Table 2 Parameter settings in algorithm表2 算法中參數的設置

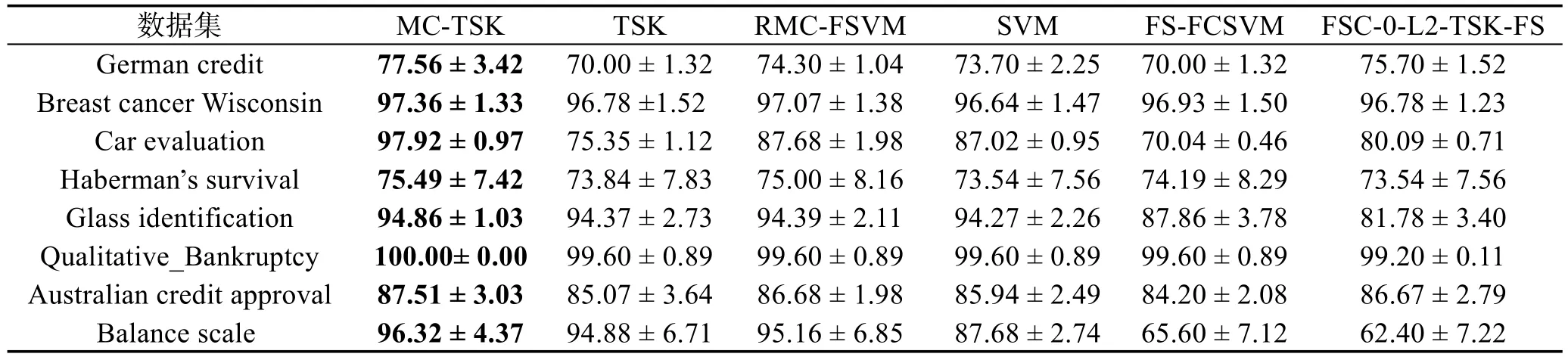
Table 3 Comparison of classification accuracy of different datasets in 6 classifiers(means+std)表3 6種分類器在不同數據集上的分類精度對比（means+std） %

綜上所述，在處理單調分類問題時，在分類器中添加單調約束可以有效提高分類器在單調數據集上的分類性能。

5 結束語

本文提出了一個單調TSK模糊系統模型用于單調分類場景，通過引入單調性的先驗知識，將單調約束添加在原始的TSK模糊系統模型，提升模型的泛化性能。將改進后的模型應用到8個單調的數據集中，結果表明在單調分類問題中，本文提出的方法在泛化性能方面要優于傳統的TSK模糊系統分類器，并且通常情況下也優于其他經典分類器。

本文提出的改進算法可以確保產生的分類器是單調的，并且由于單調約束的構建是通過約束決策屬性相對于特征的偏導數的符號，基本上避免了信息的丟失，不需要對數據集進行預處理。

在實踐中，數據采集過程很容易受到不同干擾，因此數據可能不完全遵循先驗知識的特點，比如本文的單調性。后面還擬通過添加不同水平的噪聲來模擬不同程度的違反單調性的情況，進而研究數據違反單調性是如何影響學習過程的。