考慮區間元素個數的區間猶豫模糊決策方法*

阮傳揚，韓莉娜

1.廣東財經大學 工商管理學院，廣州 510320

2.上海交通大學 安泰經濟與管理學院，上海 200030

3.廣東省生產力促進中心，廣州 510070

1 引言

近年來，由于決策環境的不確定性以及人類認知的局限性，傳統的決策方法很難適應時代潮流，已然無法解決現實中的很多決策問題，相應的模糊決策理論應運而生。自文獻[1]提出能夠刻畫模糊現象和解決模糊問題的模糊集以來，隨著時代的進步，相關學者對其進行了擴展[2-3]，目前模糊集及其擴展理論廣泛應用于模式識別、智能控制、項目投資、人事評估等實際決策問題中[4]。傳統的模糊集及其擴展形式因不能有效刻畫猶豫信息而受到約束，文獻[5-6]提出了一種能夠有效反映猶豫信息的猶豫模糊集理論，其最大特點是允許一個屬性同時出現不同的評估值，可以有效避免決策信息的缺失。然而，大多實際決策問題中，猶豫信息往往很難用精確的評估值來表達，因而文獻[7]將區間數與猶豫模糊信息相結合提出了區間猶豫模糊集，即用多個區間數表示出現的可能隸屬度。

目前有關區間猶豫模糊集的信息集成、距離測度、相關系數等已被應用到諸多領域，例如工廠選址、杰出人才評估、水庫運營模式選擇、云計算安全評估、應急預案評估、能源項目評估等[8-15]。距離測度是運用區間猶豫模糊信息進行多屬性決策的一項關鍵方法，文獻[16]定義了區間猶豫模糊距離公式，并在此基礎上構造了區間猶豫模糊標準化公式，之后提出一種區間猶豫模糊灰色妥協關聯決策方法，并將其有效應用于云計算安全評估的實例中。文獻[17]將熵值引入到區間猶豫模糊集中，提出了基于熵值的區間猶豫模糊距離測度和相似度公式，并將其應用于軟件評價問題中。文獻[18]提出了基于區間猶豫模糊信息的漢明距離、歐氏距離以及豪斯道夫距離的具體表達式，并將其有效應用于多屬性決策問題中。在上述區間猶豫模糊距離測度中，不同的區間猶豫模糊元所含區間元素個數可能存在差異，目前采用的一種方法就是在含有區間元素較少的區間猶豫模糊元中人為添加區間元素，缺點就是主觀隨意性過大，隨著決策者風險態度的不同，備選方案排序也會隨著發生變化，很難做到備選方案排序的最終統一。針對人為添加元素的問題，文獻[19]首先給出了猶豫模糊集猶豫度的概念，之后在此基礎上給出了符號距離的定義，有效解決了這個問題，但是該種方法未將猶豫模糊元中元素個數的影響考慮進去，在某些情況下決策結果不理想，具有一定程度的局限性。文獻[20]經過深入分析，發現上述區間猶豫模糊距離測度定義中僅考慮了不同區間猶豫模糊元之間的差異，忽視了區間猶豫模糊元的個數之間的差異，這一缺陷將會直接影響實際決策問題中的決策效果。文獻[21]考慮到了決策者分歧程度以及元素個數的雙重影響，提出了基于猶豫模糊信息的改進猶豫度的概念，并以此為基礎給出了猶豫模糊集的改進符號距離的定義，做到了一定程度的應對，但是元素個數的影響過大，甚至超過了元素本身數值及其離散程度的影響，在元素個數偏少或相差不大的情況下會導致決策結果與直觀認識情況不符的現象。

鑒于此，本文首先給出一種基于區間猶豫模糊信息的改進猶豫度與改進符號距離的概念。其次，針對區間猶豫模糊元中的區間元素個數和方差構造一種區間猶豫度，基于區間猶豫度提出相應的區間符號距離，可以很好地反映決策群體的分歧程度且區別度明顯。最后，給出了一種具有屬性優先級的區間猶豫模糊決策方法，并將其應用于項目投資的實際決策問題中，以此驗證本文所提方法的有效性和合理性。

2 基礎理論

為了解決同一屬性中同時出現不同區間評估值的現象，文獻[7]在猶豫模糊集的基礎上給出了區間猶豫模糊集的概念。

定義1[7]設X={x1,x2,…,xn}是一個非空集合，則稱：

區間猶豫模糊元的運算法則如下：

定義 2[7]設為3個區間猶豫模糊元，且λ≥0，則它們之間的運算法則如下：

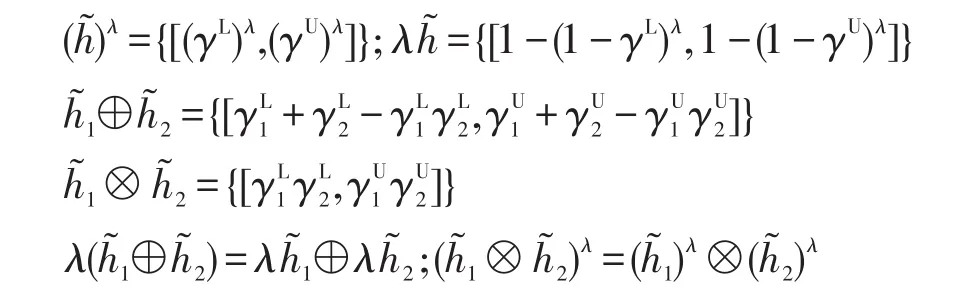
基于區間數的定義，文獻[22]給出了區間數之間的相關運算法則如下：

定義3[22]設為一組區間數，且λ≥0，則它們之間的運算法則如下：

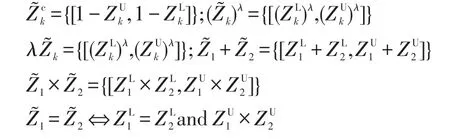
另外，均值以及方差如下：

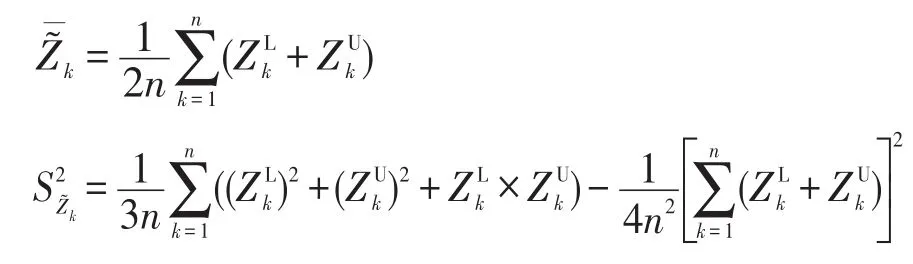
猶豫模糊元中的元素反映了決策者的分歧或猶豫程度，元素之間偏差越大，猶豫程度越高。為了反映決策者的猶豫程度，文獻[19]定義了猶豫模糊元的猶豫度。

定義4[19]設h={γi|i=1,2,…,lh}為一個猶豫模糊元，γi為h中第i小的元素，lh為h的元素個數，則h的猶豫度如下：

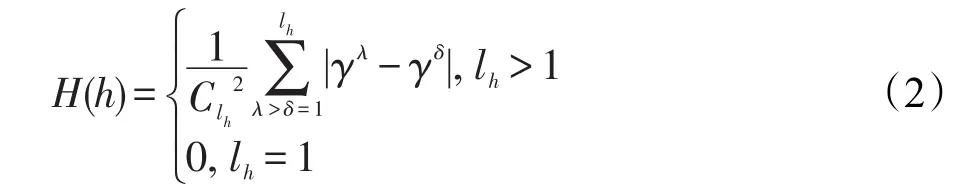
基于定義4的猶豫度，文獻[19]定義了猶豫模糊符號距離，定義如下：

定義5[19]設h={γi|i=1,2,…,lh}為一個猶豫模糊元，γi為h中第i小的元素，lh為h的元素個數，采用猶豫模糊元最大值1ˉ為理想點猶豫模糊元，則由h到1ˉ的符號距離如下：

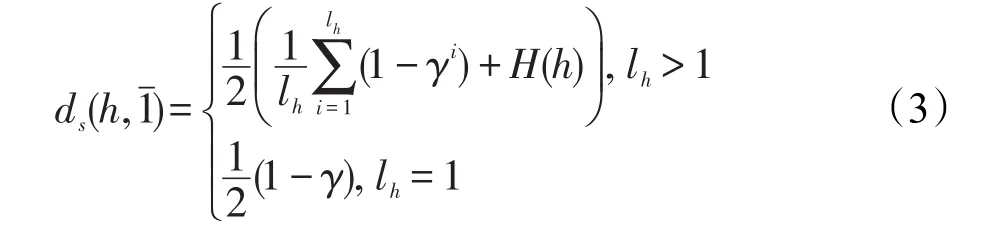
猶豫模糊信息體現的是決策者的不同意見，猶豫模糊元中在“重復決策數據僅保留一個”的情況下元素越少，表示意見越統一，為了考慮猶豫模糊元中的元素個數對決策結果的影響，文獻[21]提出了一類改進的猶豫度和符號距離。

定義6[21]設h={γi|i=1,2,…,lh}為一個猶豫模糊元，γi為h中第i小的元素，lh為h的元素個數，則h的改進猶豫度如下：

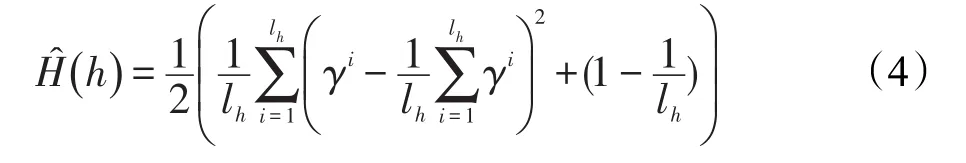
定義7[21]設h={γi|i=1,2,…,lh}為一個猶豫模糊元，γi為h中第i小的元素，lh為h的元素個數，1~為理想點猶豫模糊元，則稱:

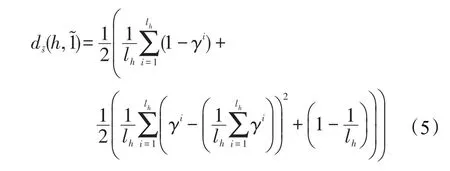
為h到?的改進符號距離。

3 基于區間猶豫模糊信息的多屬性決策方法

猶豫模糊信息揭示的是決策者的不同意見，具有很大的不確定性，這種不確定性加大了決策的難度，為了有效測度這種分歧度，決策者進行決策時通常給出的是區間猶豫模糊信息，鑒于此，本文給出一種基于區間猶豫模糊信息的區間猶豫度的概念，并在此基礎上給出基于區間猶豫模糊信息的區間符號距離的定義，之后將其應用于屬性之間具有優先級關系的猶豫模糊決策問題中。

3.1 基于區間猶豫模糊信息的符號距離

為了對決策信息進行有效處理，距離測度近年來被有效應用于多屬性決策中，文獻[21]考慮到了決策者分歧程度以及元素個數的雙重影響，給出了改進的猶豫度和符號距離的概念，本文基于此給出了一種基于區間猶豫模糊信息的改進猶豫度和符號距離的定義。

定義 8設為一區間猶豫模糊元，?的區間元素個數，則?的改進猶豫度如下：

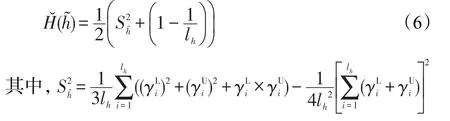
表示區間猶豫模糊元的方差。

定義 9設為一區間猶豫模糊元，?的區間元素個數?為理想點猶豫模糊元，則?的改進符號距離如下：

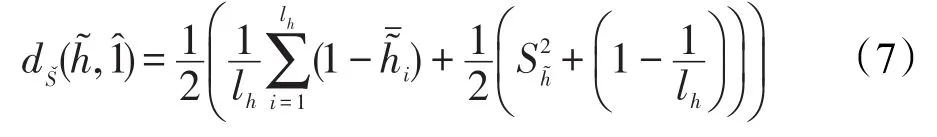
然而，定義8和定義9對元素個數的處理上并未完全到位，例如，若存在3個元素數量不等的區間猶豫模糊元改進猶豫度為改進符號距離為通 過 分 析以上結果可知：在元素個數偏少且大于1的情況下，區間猶豫模糊集中區間元素個數的影響過大，甚至超過了區間元素本身數值及其離散程度的影響，極有可能導致最終決策結果與直觀認識情況不符的現象。

為解決這類問題，本文引入對數變換的概念，主要是由于對數變換是數據變換的一種常用方式，其目的在于使數據的呈現方式接近所希望的前提假設，從而可以更平滑地進行統計推斷。例如：經濟數據大多數都是偏態分布，比如收入GDP之類的，而且大多是右偏的，取對數后不會改變數據的性質和相關關系，但壓縮了變量的尺度，從而形成正態分布的數據，這樣數據更加平穩，也削弱了模型的共線性、異方差性等。因此，本文給出一種基于區間猶豫模糊信息且含有對數變換的區間猶豫度的概念，之后在此基礎上給出基于區間猶豫模糊信息的區間符號距離的定義，并討論其基本性質。

定義 10設為一區間猶豫模糊元，?的區間元素個數，則?的區間猶豫度如下：

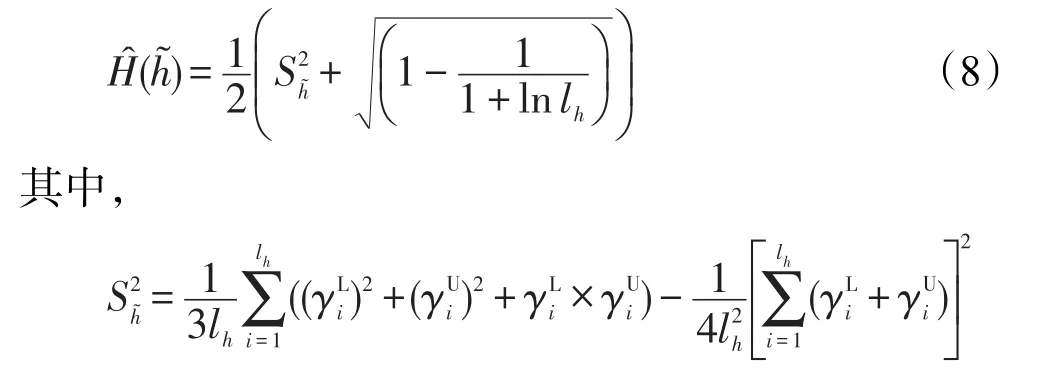
表示區間猶豫模糊元的方差。

式（8）為基于區間猶豫模糊元中區間元素的方差以及個數定義的區間猶豫度，偏差越大，區間元素個數越多，所對應的區間猶豫度也越大。

區間猶豫度滿足如下性質[19,21]：

性質 1設為一區間猶豫模糊元，其對應的補集為

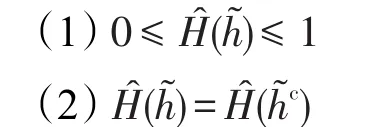
易于驗證式（8）滿足性質1。

證明（1）由于方差的取值范圍為[0,1]，則

（2）由補集的方差：

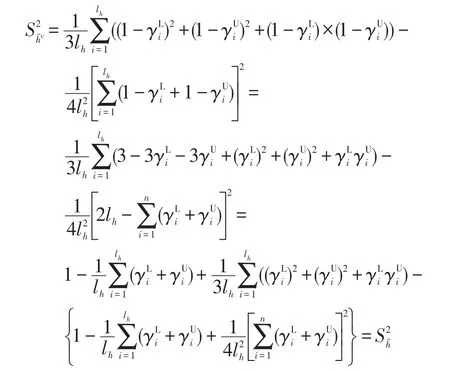
而區間猶豫模糊元中的區間元素數量lh恒定，則恒成立。 □

基于區間猶豫模糊信息的區間猶豫度，可以得到一種相應的區間符號距離。

定義11設為一區間猶豫模糊元，?的區間元素個數，1?為理想點猶豫模糊元，則?的區間符號距離如下：

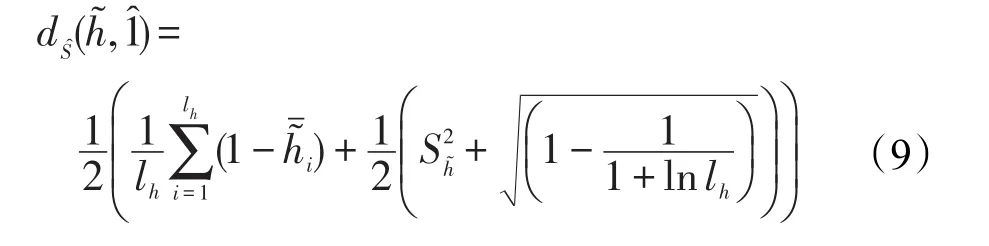
區間符號距離滿足如下性質[19,21]：

性質 2設為 3 個區間猶豫模糊元，1?為理想點猶豫模糊元，則：

3.2 考慮屬性優先級的屬性權重確定方法

本文給出一種考慮屬性優先級的混合加權方法，保證該方法既能考慮屬性優先級，又能包含屬性信息的離散程度。詳細步驟如下[23]：

（1）決策專家組給出屬性優先級信息。

（2）通過計算第j項屬性的基于區間猶豫模糊信息的區間符號距離方差ej來確定相鄰優先級屬性xj與xj+1重要性程度之比rj。

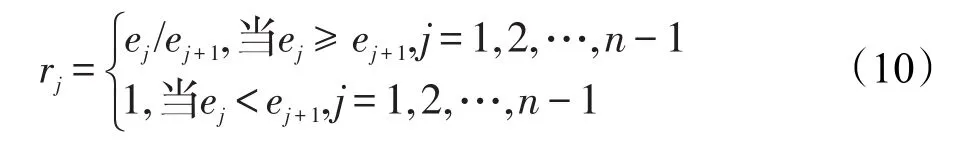
其中，令rn=1。

（3）根據給出的rj值，按照屬性優先級從高到低的順序計算優先級排序在第k個屬性的權重tk為：

3.3 區間猶豫模糊多屬性決策步驟

基于式（9）的區間符號距離以及式（11）屬性權重確定方法，給出一種屬性具有優先級關系的區間猶豫模糊多屬性決策方法。假設方案集為A={A1,A2,…,Am}，屬性集為G={G1,G2,…,Gn}，其對應的權重向量為專家組E={e1,e2,…,ep}中每位專家在進行匿名評價時給出每個方案Ai∈A關于每個屬性Gj∈G的區間評價值，去掉完全重復的區間元素，就組成了一個區間猶豫模糊決策矩陣是一個區間猶豫模糊元。

基于區間符號距離和屬性優先級的區間猶豫模糊多屬性決策步驟如下：

步驟1專家組給出每個方案Ai∈A關于每個屬性Gj∈G的區間評價值，得到區間猶豫模糊決策矩陣H=(hij)m×n。

步驟2首先利用式（9）計算區間符號距離，其次依據式（11）得出具有屬性優先級的權重信息W=(ω1,ω2,…,ωn)T。

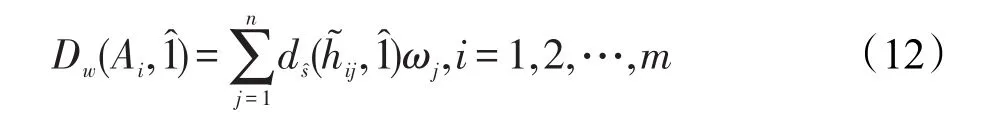
步驟3利用式（12）中的加權符號距離公式：得出各方案A={A1,A2,…,Am}的加權符號距離并根據的大小對各方案進行排序，加權符號距離?越小，相應的方案Ai越優。

4 數值算例分析

深圳一國際投資銀行準備將一筆資金用于市場投資，假設目前備選方案為：軟件公司A1、旅游公司A2、食品公司A3、汽車公司A4和建筑公司A5。為了客觀科學進行決策，該投資銀行的領導層邀請相關專家進行決策，專家組決定在發展潛力G1、投資安全系數G2、收益率G3以及產品替代性G4這4個屬性下進行綜合評估，并且屬性權重向量未知，但決策小組事先給出了屬性優先級關系G4?G1?G2?G3，專家小組給出每個方案Ai∈A關于每個屬性Gj∈G的評價區間值，去掉完全重復的區間數據，就組成了一個基于區間猶豫模糊信息的決策矩陣{[0.3,0.4],[0.5,0.6]}表示第2個公司（即旅游公司）在第1個屬性（即發展潛力）方面專家小組有兩種不同觀點，即方案A2關于屬性G1的評價區間值有[0.3,0.4]和[0.5,0.6]兩種。

為了獲得最佳投資公司，基于區間符號距離的多屬性決策步驟如下：

步驟1專家組給出每個方案Ai∈A關于每個屬性Gj∈G的區間猶豫模糊決策矩陣，見表1所示。

步驟2首先利用式（9）計算區間符號距離，見表2。其次依據式（11）得出屬性權重：

W=(0.305 1,0.215 9,0.173 9,0.305 1)T

步驟3利用式（12）中的加權符號距離公式得出各方案A={A1,A2,…,Am}的加權符號距離

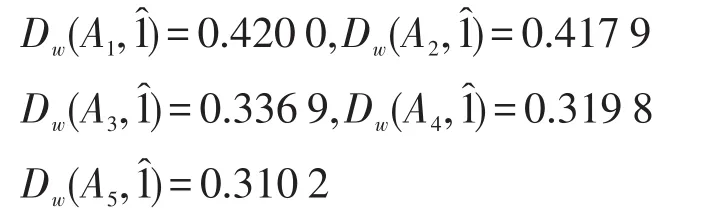
Table 1 Interval-valued hesitant fuzzy decision making matrix表1 區間猶豫模糊決策矩陣

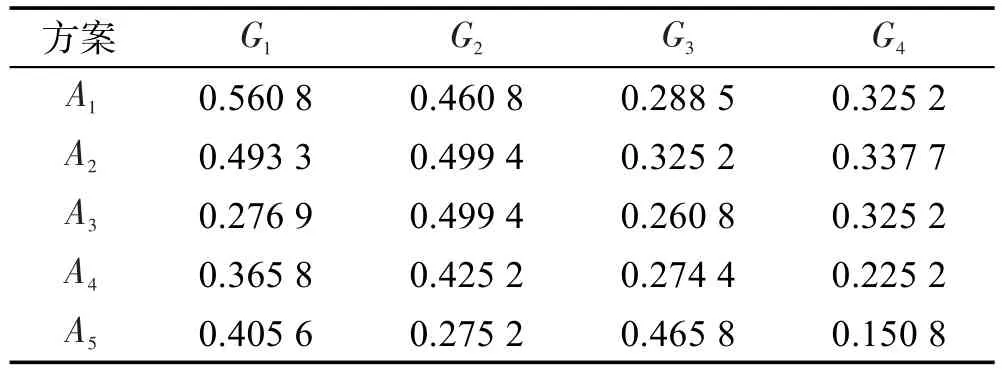
Table 2 Interval-valued signed distance matrix表2 區間符號距離

為了獲得最佳投資公司，若采用定義9改進符號距離的話，具體多屬性決策步驟如下：

步驟1′同步驟1。

步驟2′首先利用定義9計算改進符號距離，見表3。其次依據式（11）得出屬性權重：

W=(0.317 8,0.182 2,0.182 2,0.317 8)T

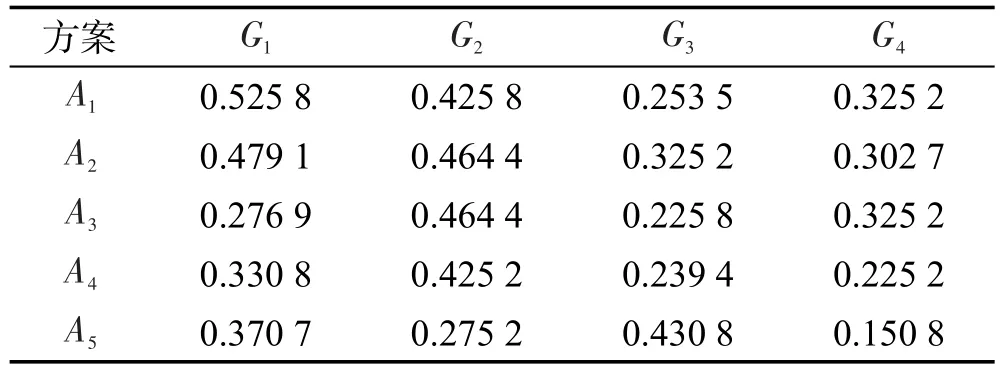
Table 3 Improved signed distance matrix表3 改進符號距離

步驟3′利用式（12）中的加權符號距離公式得出各方案A={A1,A2,…,Am}的加權符號距離

由以上結果可知，本文所述方法主要優勢以及適用條件如下：

（1）采用基于區間猶豫模糊信息的區間符號距離法進行決策時不僅考慮了區間猶豫模糊元中區間元素的均值大小以及離散程度等影響，還考慮了區間猶豫模糊元素個數的影響，包含的范圍比較廣，所得決策結果具有較好的區分度和穩定性，有效性也更高。

（2）本文基于屬性優先級和區間猶豫模糊符號距離建立的屬性權重確定方法屬于主客觀組合賦權方法，既能保持屬性優先級恒定，又能有效利用已有區間評價信息科學合理地確定出屬性權重，數值案例表明該方法所得決策結果合理、可靠。

（3）由數值案例可知，在區間猶豫模糊決策矩陣中區間元素較少的情況下，區間符號距離適用范圍比較廣，所得決策結果合理、有效。不過，當決策矩陣中區間猶豫模糊集中區間元素較多時，由于定義11中有關區間猶豫模糊元素個數的計算公式部分隨著區間元素個數的增大而趨向于1，則區間元素個數對決策結果的影響不大且計算復雜度較高。因此，這種情況下采用文獻[17-19]等經典算法比較合適。

5 結束語

本文基于區間猶豫模糊元中區間元素的方差與個數提出了一類區間猶豫模糊符號距離，并在此基礎上研究了屬性具有優先級關系的多屬性決策問題。主要工作如下：

（1）為了考慮元素個數的影響，利用文獻[21]中基于猶豫模糊信息的改進猶豫度和改進符號距離，給出了基于區間猶豫模糊信息的改進猶豫度和改進符號距離的定義。

（2）基于區間猶豫模糊元中區間元素的方差與個數定義了一種含有對數函數的區間猶豫度，以便合理反映決策者的分歧程度。

（3）基于區間猶豫度定義了一種同時考慮區間猶豫模糊元中區間元素大小、數量和方差的區間猶豫模糊符號距離，通過數值案例可知區間猶豫模糊符號距離具有區分度明顯，決策結果更加合理、可靠的特點。

（4）針對屬性具有優先級的多屬性決策問題，本文基于區間猶豫模糊符號距離和屬性優先級提出了一種屬性權重確定方法，之后利用加權符號距離對備選方案進行排序。

采用本文方法進行決策時同時考慮了區間猶豫模糊元中區間元素的大小、數量、離散程度等多重影響，因而決策結果具有較好的區分度和穩定性。