面向屬性的區間集概念格*

賀曉麗，魏 玲，錢 婷

1.西北大學 數學學院，西安 710127

2.西安石油大學 理學院，西安 710065

1 引言

形式概念分析[1-2]（formal concept analysis，FCA）是由德國數學家Wille于1982年以重建格理論為目的提出的一種數學理論。它的數據表現形式為二維交叉表即形式背景。形式背景(G,M,I)是一個由對象集G，屬性集M以及G與M間二元關系I構成的三元組。在形式背景上，通過一對伽羅瓦連接可以形成概念(X,B)，其中X為概念的外延，是屬于這個概念的所有對象的集合；而B為內涵，是所有這些對象所共同具有的屬性（或特征）集。概念格是知識的一種表現形式，也是數據處理的一種工具。

形式概念分析與其他理論的融合研究是其理論研究的一個重要方面，迄今為止已產生諸多頗有意義的研究成果。例如，與三支決策理論結合，祁建軍等人[3]提出了三支形式概念分析理論；與粒計算理論相結合，Belohlávek等人[4]給出了多尺度形式背景中的概念格構建理論與算法，在此方面更為詳細的研究可參看李金海和吳偉志[5]所給出的綜述研究；與模糊集理論相結合，Belohlávek[6-8]提出了模糊形式背景和模糊概念格；與粗糙集理論相結合，Düntsch和Gediga[9]提出了面向屬性概念格，類似地，Yao[10]定義了面向對象概念格。與描述不完備信息的區間集理論相結合，馬建敏等人[11]引入了區間集概念格。其本質思想是把概念中表示外延與內涵的集合推廣到區間集，利用區間集所反映的不確定信息把經典概念擴展到區間集概念。隨后，對區間集概念格的構造理論進行了研究[12]。在不完備形式背景上，Yao[13]提出了區間集算子，并對李金海等人[14]提出的近似概念格進行了相應的區間集表示。

已經知道，面向屬性概念格是粗糙集與概念格相結合的一種數據分析理論，鑒于粗糙集與區間集更為密切的聯系，本文擬將區間集思想引入到面向屬性概念格框架之中，給出了面向屬性的區間集概念格構造方法及相應的建格算法。

本文組織結構如下：第2章回顧概念格、面向屬性概念格和區間集等相關定義；第3章提出一對新的伽羅瓦連接，并在此基礎上定義了面向屬性的區間集概念及面向屬性的區間集概念格；進一步研究面向屬性概念格與面向屬性的區間集概念格之間的關系，同時給出面向屬性的區間集概念格的構造方法及相應的建格算法；第4章進行了總結和展望。

2 基礎知識

定義1[1]設(G,M,I)為一形式背景，對象集X?G和屬性集A?M上定義了一對對偶算子如下：

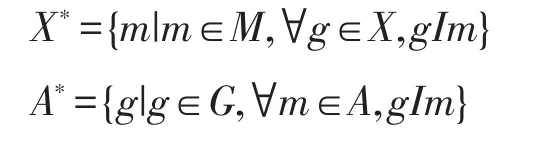
若X?=A且A*=X，則稱(X,A)為形式背景(G,M,I)的一個概念。記形式背景(G,M,I)的所有概念構成的集合為L(G,M,I)，在L(G,M,I)上，定義二元關系“≤”為：

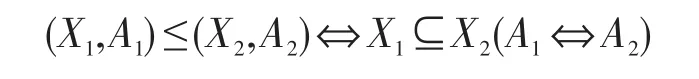
(L(G,M,I),≤)在偏序關系“≤”形成完備格，稱(L(G,M,I),≤)為概念格。

定義2[9]設(G,M,I)為一形式背景，↑和↓是2G與2M之間的一對算子，X↑={m∈M|m*?X≠?}A↓={g∈G|g*?A}。若X↑=A且A↓=X，則稱 (X,A)為面向屬性概念。其中，X為面向屬性概念的外延，A為面向屬性概念的內涵。記形式背景(G,M,I)的所有面向屬性概念構成的集合為PL(G,M,I)。在PL(G,M,I)上，定義二元關系 ≤ 為：(X1,A1)≤(X2,A2)?X1?X2(A1?A2)。容易證明“≤”是偏序關系且(PL(G,M,I),≤)在偏序關系“≤”形成完備格，即任意的兩個概念(X1,A1),(X2,A2)的上確界和下確界為：

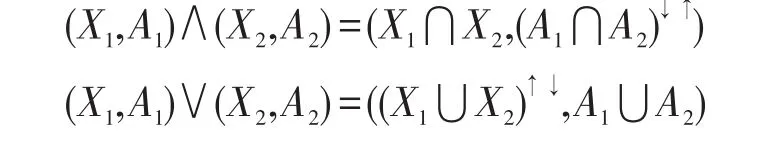
稱(PL(G,M,I),≤)為面向屬性概念格。

定義3[15]設U是有限論域，2U為U的冪集。定義X=[X1,X2]={XΔ∈2U|X1?XΔ?X2}，稱為U的區間集。對于任意的X∈2U，X可以看成是由區間集[X,X]退化得到的。U上所有的區間集構成的集合記為I(2U)。類似于經典集合之間的運算，Yao給出了區間集間的運算[15]。

定義4[15]設U是有限論域，X,Y是U上的區間集，即X=[X1,X2]，Y=[Y1,Y2]∈I(2U)，定義：

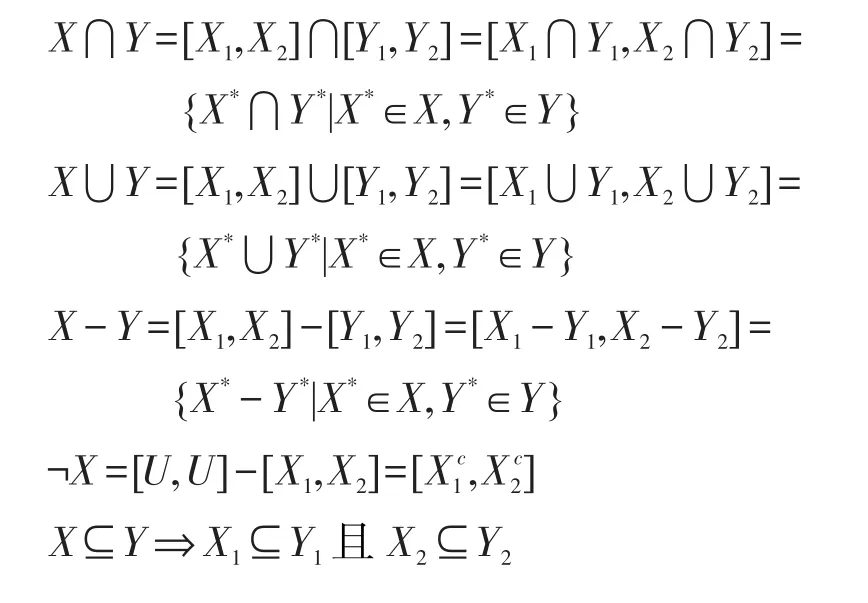
3 面向屬性的區間集概念格

3.1 面向屬性的區間集概念格的定義

定義5設(G,M,I)為一形式背景，對于任意的X=[X1,X2]∈I(2G)，A=[A1,A2]∈I(2M)，定義I(2G)與I(2M)之間的一對算子?:I(2G)→I(2M)和?:I(2M)→I(2G)如下：

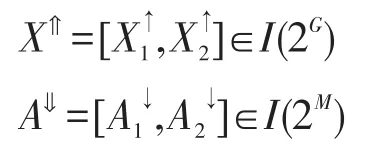
例1(G,M,I)為一個形式背景（如表1所示），其中G={1,2,3}，M={a,b,c}。

取X=[3,13]∈I(2G),A=[c,ac]∈I(2M)，按照定義5，有 [3,13]?=[3↑,13↑]=[c,ac]，[c,ac]?=[c↓,ac↓]=[3,13]。

Table 1 Formal context(G,M,I)表1 形式背景(G,M,I)

性質1設(G,M,I)為一形式背景，對于任意的X=[X1,X2]∈I(2G)，A=[A1,A2]∈I(2M)，I(2G)與I(2M)之間的一對算子?:I(2G)→I(2M)和?:I(2M)→I(2G)，則?和?具有以下性質：

（1）X?Y?X??Y?

（2）A?B?A??B?

（3）X?X??,A???A

（4）X=X???,A???=A

（5）(X?Y)?=X??Y?,(A?B)?=A??B?

證明下面僅證明（5）。

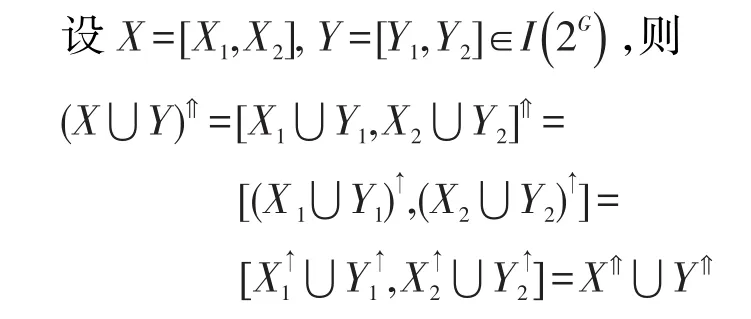
類似可證明(A?B)?=A??B?。 □

定義6設(G,M,I)為一形式背景，?X∈I(2G),A∈I(2M)，若X?=A且A?=X,則稱 (X,A)為面向屬性的區間集概念。其中，X稱為面向屬性的區間集概念的外延，A稱為面向屬性的區間集概念的內涵。

記形式背景(G,M,I)的所有面向屬性的區間集概念構成的集合為PIL(G,M,I)，所有面向屬性的區間集概念的外延構成的集合為PILG(G,M,I)，所有面向屬性的區間集概念的內涵構成的集合為PILM(G,M,I)，定義PIL(G,M,I)上的二元關系為：(X,A)≤(Y,B)?X?Y(A?B)。

很容易證明上述的二元關系“≤”是偏序關系且在此偏序關系下，PIL(G,M,I)形成完備格，即對任意的兩個概念(X,A)、(Y,B)的下確界和上確界分別如下所示：

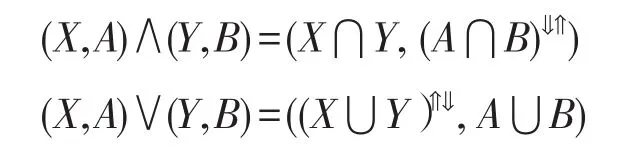
例2（續例1） 因為X=[3,13],A=[c,ac]，由例1知X?=[c,ac]=A,A?=[3,13]=X，所以由定義6知 (X,A)是面向屬性的區間集概念。類似地，可以求出此形式背景的所有面向屬性的區間集概念及其相應的面向屬性的區間集概念格PIL(G,M,I)。格圖如圖1所示。

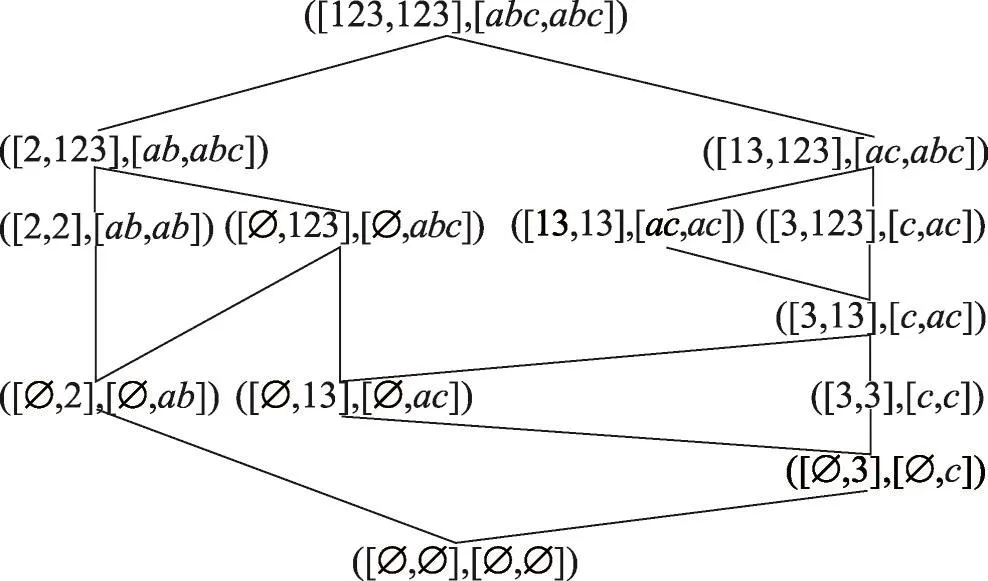
Fig.1 Property oriented interval-set concept lattice of Table 1圖1 表1的面向屬性的區間集概念格

3.2 面向屬性概念格與面向屬性的區間集概念格的關系

本節從元素、集合及代數結構的角度研究面向屬性概念格與面向屬性的區間集概念格之間的關系。

為了研究集合PIL(G,M,I)與集合PL(G,M,I)之間的關系，記：

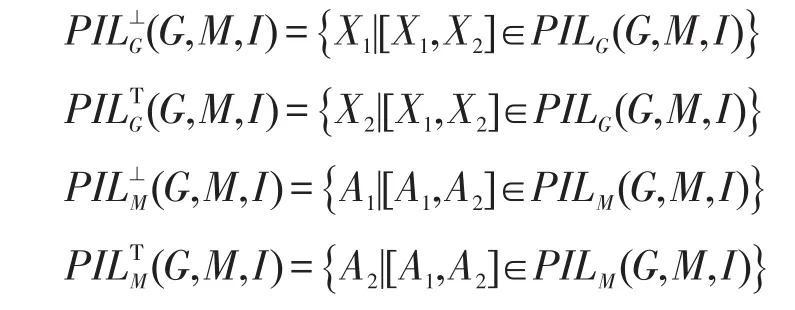
定理3設(G,M,I)為一個形式背景，PL(G,M,I)為其相應的面向屬性概念格，PIL(G,M,I)為其相應的面向屬性的區間集概念格，則下列式子成立：

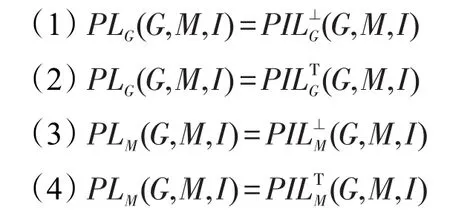
上面定理1及定理2從元素上研究了面向屬性概念格與面向屬性的區間集概念格間的關系，而定理3從集合整體上進一步研究了兩者之間的關系。下面將從代數結構上探討兩者之間的關系。

定理4設(G,M,I)為一個形式背景，PL(G,M,I)為其相應的面向屬性概念格，PIL(G,M,I)為其相應的面向屬性的區間集概念格，則存在一個映射f:PL(G,M,I)→PIL(G,M,I)使得f(PL(G,M,I))是PIL(G,M,I)的一個子格。

證明對于任意的(X,A)∈PL(G,M,I)，定義f(X,A)=([X,X],[A,A])。由定理1知 ([X,X],[A,A])∈PIL(G,M,I)，故f是從PL(G,M,I)到PIL(G,M,I)的一個映射。從而f(PL(G,M,I))是PIL(G,M,I)的一個非空子集。下面證明f(PL(G,M,I))對∧，∨封閉。

（1）對于任意的 ?1,?2∈f(PL(G,M,I))，存在 (X,A)，(Y,B)∈PL(G,M,I)，使得：

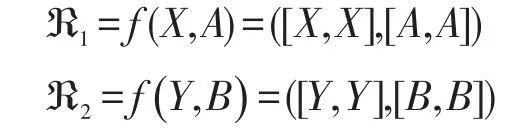
由定義6知：

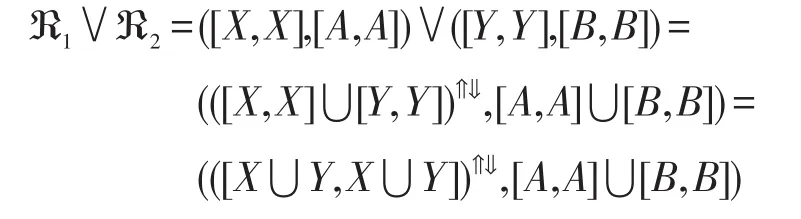
由面向屬性概念格中的上確界定義知，對于上述的 (X,A),(Y,B)∈PL(G,M,I)，則 (X,A)∨(Y,B)=((X?Y)↑↓,A?B)∈PL(G,M,I)，由f的定義知：

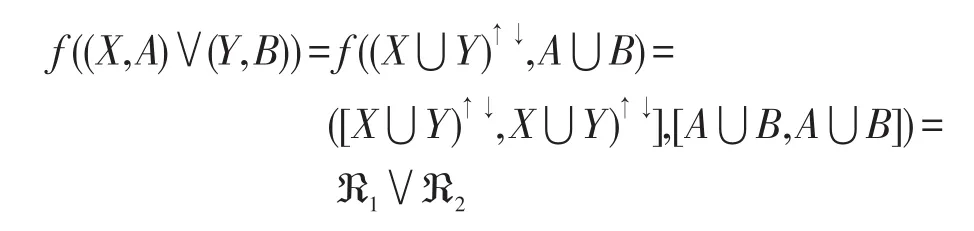
因此?1∨?2∈f(PL(G,M,I))。

（2）對于任意的 ?1,?2∈f(PL(G,M,I))，存在(X,A),(Y,B)∈PL(G,M,I)，使得：

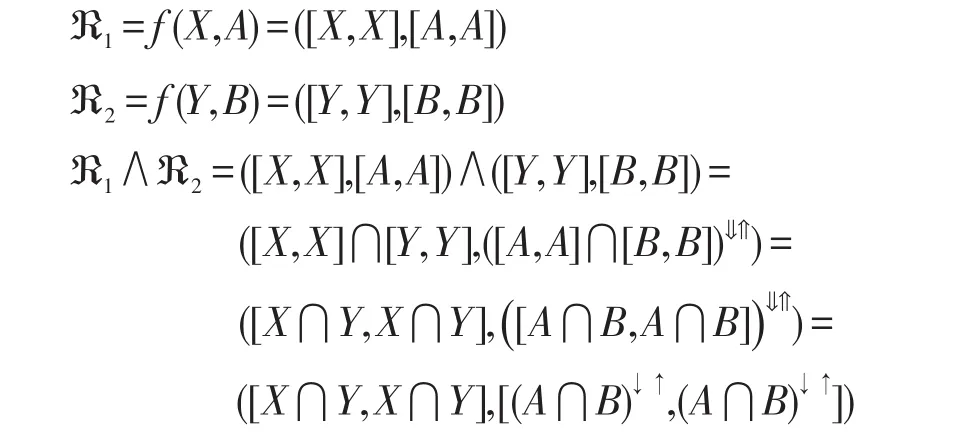
由面向屬性概念格中下確界的定義知，對于(X,A),(Y,B)∈PL(G,M,I)，則：

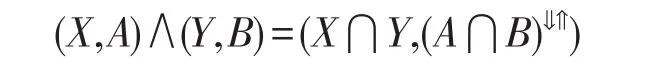
因此，由f的定義知：

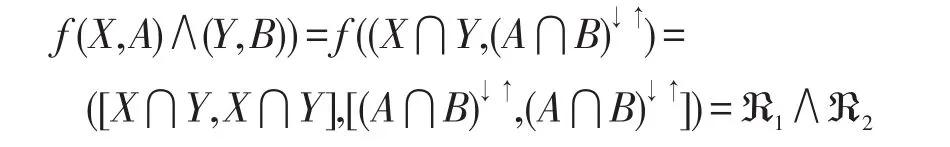
從而，?1∧?2∈PIL(G,M,I)。故f對∧封閉。

綜上所述f(PL(G,M,I))是PIL(G,M,I)的一個子格。 □

定理5設(G,M,I)為一個形式背景，PL(G,M,I)為相應背景的面向屬性概念格，若對于任意的(X1,A1)，(X2,A2)∈PL(G,M,I)且X1?X2，則：

因此(X,A)∈PIL(G,M,I)。 □

3.3 面向屬性的區間集概念格的構造

基于上述二者之間的關系，給出面向屬性的區間集概念格的構造方法。

定理6設(G,M,I)為一個形式背景，PL(G,M,I)為其相應的面向屬性概念格，PIL(G,M,I)為其相應的面向屬性的區間集概念格，則：

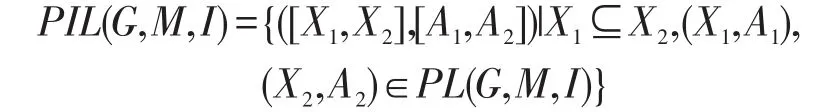
證明記 ? ={([X1,X2]，[A1,A2])|X1?X2,(X1,A1),(X2,A2)∈PL(G,M,I)}，由定理2知，PIL(G,M,I)??，又由于定理5知??PIL(G,M,I)，故?=PIL(G,M,I)。 □

例3（續例1）利用定理6構造表1的面向屬性的區間集概念格。通過定義2可計算出面向屬性概念的外延為：并由上述外延構成的區間集有：[? ,? ],[? ,2],[? ,3]，[? ,13]，[? ,123]，[2,2]，[2,123][3,3],[3,13],[3,123]，[13,13]，[13,123]，[123,123]。由定理6知，面向屬性的區間集概念有([?,?],[?,? ]),([? ,2],[? ,ab]),([? ,3],[? ,c]),([? ,13],[? ,ac]),([? ,123],

利用圖1，可驗證上述所求的面向屬性概念正確。依據定理6，給出相應的算法。

算法1面向屬性的區間集概念格構造的算法

輸入：形式背景(G,M,I)。

輸出：面向屬性的區間集概念格PIL(G,M,I)。

1.PIL(G,M,I)=? ，PL(G,M,I)=?

2.調用求面向屬性概念格的算法[16]計算PL(G,M,I).

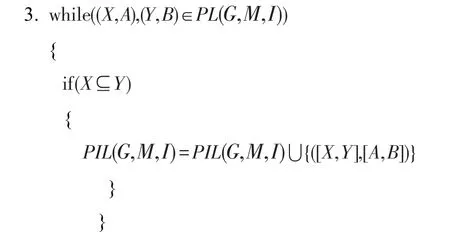
4 總結與展望

本文主要給出了面向屬性的區間集概念格的定義，并研究了面向屬性的區間集概念格與面向屬性概念格之間的關系，最后給出了面向屬性概念格的構造方法及其相應的算法。對于本文所提的研究對象，將研究其相應的屬性約簡及壓縮問題，對所獲知識進行凝練提取。另外，還可以將此思想引入到其他理論框架中，例如引入到面向對象概念格并研究新型概念格之間的關系。