基于GARCH模型的上證50的比較研究

胡后燕

(安徽大學 經濟學院，安徽 合肥 230601)

一、VaR及波動率介紹

(一)VaR的描述

VaR一般表示在一定風險狀態下的價值，即在一定的置信水平下某個既定的持有時間內，某種金融序列或者金融組合可能會遭受的最大限度上的損失額度。對于VAR的理解需要掌握幾個要點：首先是置信水平，VAR不是一般意義上的損失額而是對應置信水平的最大損失額。其次是持有期VAR是對應持有期的潛在的最大損失額。最后就是正常市場,VaR不是極端市場的最大損失額而是正常市場中出現的最大損失[1]。從數學的角度來講VaR就是針對某個損益在預期分布里面相應的置信水平下的分為點數的值，其數學表達形式為：

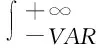
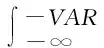
VAR的計算公式為：

式中的V0代表金融序列的初始值，δ為方差，Zα表示下分位數，T表示持有期。

(二)波動率的描述

傳統的理論一般認為市場是有效的，波動率指的是資產收益率的條件標準差，因此金融資產的波動是恒定的，金融序列的波動性基本上不會因為時間的關系改變，根據很多的實證研究結果，我們可以總結金融序列在波動性方面存在一些比較明顯的特點。如，金融序列的波動性一般在均值旁邊的點會存在比正態分布的狀態下更高的尖峰厚尾的特點，同時在分布的尾部也會看起來比正態分布寬大，分布的峰高超過3；金融序列的某一個變動后面會伴隨著一種相應的變動，這就是所謂的波動集聚效應。波動性對有利和不利消息的反應展現出不對稱的狀態，也就是說在一定的條件下，不利消息對市場的影響要超過有利消息，這就是非對稱性。金融序列收益率的絕對值展現出緩慢衰減的現象，即使相互之間有著較長的時間間隔，也還是相互間存在關聯，這就是長期記憶性所呈現的歷史對將來的影響。在一定程度上長期記憶性表明收益存在可預測性，市場上可能因為收益的可預測性產生套利行為[2]。因此有效市場假說不成立。波動性是影響上證50股票交易的因素之一，筆者側重對上證50股票收益率的波動性進行研究，考量其條件異方差模型。條件異方差模型有兩種類型，一種是從函數的角度去描述方差；另外一種是借助隨機方程來描述方差。GARCH模型就是屬于第一種類型。波動率模型主要研究資產收益率是序列相不相關，還是低階相關的，我們可以通過對金融序列的單位根檢驗圖來進行判斷。假設金融資產的收益率序列為Xt,我們知道波動率是刻畫金融序列收益率的某種相關關系，如果給定前一時刻已經獲得的信息集合是我們可以得到Xt的條件均值和條件方差，其關系式分別為：

μ=E(Xt/Ft-1)

δ2=VaR(Xt/Ft-1)=E[(Xt-μt2/Ft-1)]

上述Ft-1表示已知的信息集合，它包括了金融資產收益率的函數，在某種程度上條件異方差模型就是把一個動態方程加到一個金融序列的模型里面，這又在一定程度上闡明了資產收益率的條件異方差會順時而變的特點。

二、理論模型的介紹

(一)ARCH模型

恩格爾在1982年提出了ARCH模型，認為時間序列數據一般存在一種特殊的異方差，即自回歸條件異方差。ARCH模型的簡單形式為：

ARCH(1):Yt=βXt+εt

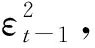
Xt=δtεt

ARCH模型認為金融序列的擾動項之間是不相關的并且相互之間也是不獨立的；金融序列收益率的某一種變動往往可能會跟著一個類似的變動。我們一般用LM檢驗、F檢驗、Q檢驗，來檢驗金融序列的ARCH效應，這里最常用的就是拉格朗日乘數法檢驗，檢驗步驟為：

H0:α1=α2=…αp如果α1=α2=…αp=0則說明不存在ARCH效應，如果其中存在一個αp不是0，說明ARCH效應是存在的。然后檢驗統計量為LM=nR2～χ2(q)這里的n代表樣本數量，R2代表輔助回歸項系數，如果原假設被推翻則認為該金融序列存在ARCH效應，反之如果原假設成立則樣本序列不存在ARCH效應。

(二)GARCH模型

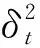
由上式可知，t期殘差的方差由其滯后一期殘差的平方和滯后一期殘差方差的平方決定，將上式進行推廣可以得到更一般的GARCH模型，即GARCH(p,q)模型，其方程形式為:

在GARCH模型里面有幾個重要的參數，即α，表示誤差系數，它在很大程度上決定了金融序列的波動性對市場運動反應的敏感度，并且α數值越大，意味著波動性的反應越迅速。α的數值通常小于0.25;β表示滯后系數，它在很大程度決定著波動性對市場運動產生反應的持久性，β的數值越大，說明產生波動越持久。β數值通常大于0.7;上述兩個參數的和(α+β)被持久稱作持久度，它的作用就是在一定程度上決定著波動性向均值反轉的速度。(α+β)的數值越大，說明持久性越強，向均值回復的速度就會更慢。

(三)TGARCH模型

不利的消息往往比有利的消息對金融資產的價格產生更大更強烈的影響，鑒于此Glosten,Jagannathan and Runkle在1993年提出了TGARCH模型。

假設條件方差方程為：

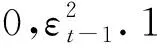
(四)EGARCH模型

EGARCH模型是由于對稱的ARCH類模型無法準確地反映正負沖擊效應而提出的改進模型，在一定程度上可以處理股價比的非對稱分布問題。它的一般形式為：

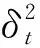
(五)PGARCH模型

PGARCH模型是由Ding在1993年提出的，它具有一套科學模型，并能進行量化計算。

三、實證分析

偏度S=-0.274635<0，峰度K=6.534878>3，這說明上證50指數收益率比正態分布的圖像偏左一些并且呈現尖峰后尾的分布狀態。

表1 數據的統計特征

圖1 上證50基本統計特征

圖1里面的后兩項是總體分布的正態性檢驗所采取的Jarque-Bera檢驗所得到的結果，我們一般假設在JB檢驗里面樣本序列一般服從正態分布，其檢驗的統計量為：

式中S表示金融樣本序列的偏動幅度，K表示金融樣本序列的峰高，m代表進行樣本序列估計時所采用的樣本系數的個數。一般在零假設的情況下，我們可以認JB統計量服從χ2(2)分布通過Eviews軟件操作的結果，我們可以判讀有沒有必要拒絕原假設。由圖1我們可以看到，這里的概率值近乎為0，則說明了在至少99%的置信水平的條件下我們可以不接受原假設，即認為金融樣本序列不服從正態分布。

緊接著利用QQ圖做驗證，見圖2。

通過圖2我們可以看到，金融序列樣本的值在一起呈現出一條彎曲的線，與圖中傾斜45°的直線相偏離，即此金融序列不是正態分布。

(一)平穩性檢驗

檢驗上證50指數對數收益率的單位根得如下結果，見表2。

表2 上證50對數收益率序列的單位根檢驗圖

由此可以知道上證50對數收益率的單位根相較于臨界值小，說明這個金融序列較為穩定，繼續檢驗相關和偏自相關性如下：

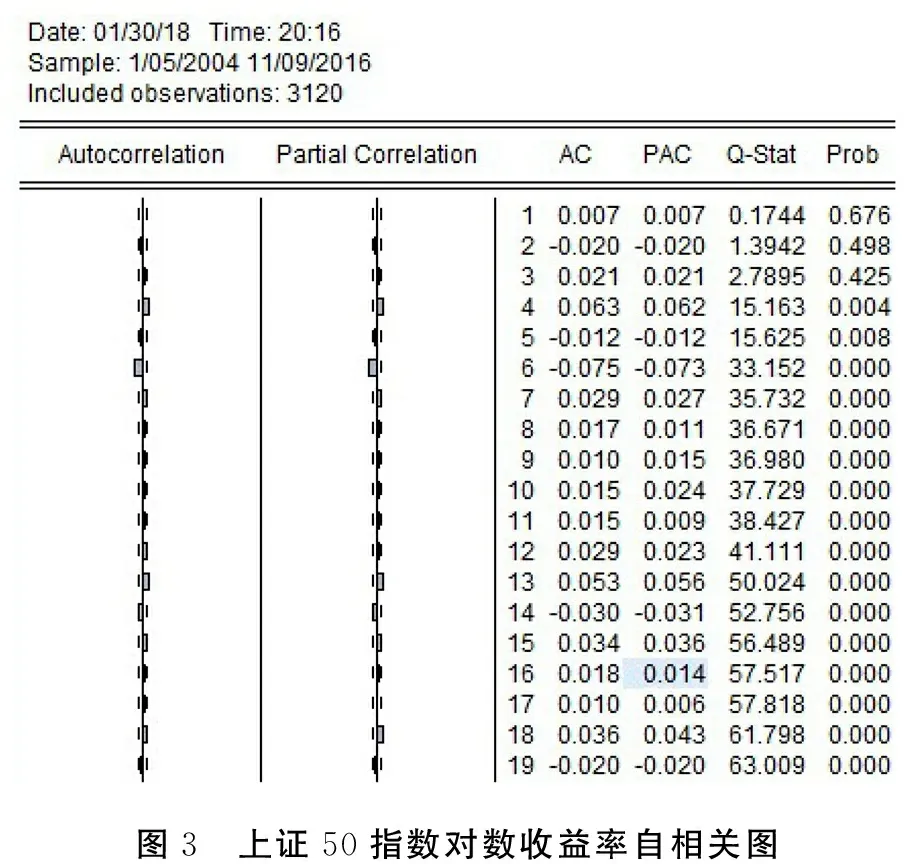
圖3 上證50指數對數收益率自相關圖

根據圖3，我們可以利用上證50的三階滯后量來求自相關函數值和偏自相關函數值，得知上證50指數的對數收益率之間的關聯度不明顯，但是在更高階之后關聯度呈現明顯的現象。

(二)檢驗條件異方差性

進行條件異方差檢驗就是判斷金融序列是否存在ARCH效應，可以通過上面的結果知道樣本平方回報率存在著自相關性，緊接著用兩種方式檢查是不是存在條件異方差。

1.檢驗殘差圖法

由圖4，可以得知殘差序列存在波動集聚效應，認為金融序列存在條件異方差。

2.檢驗ARCH效應

一般根據ARCH效應的存在與否來判斷隨機擾動項是否存在GARCH效應，利用拉格朗日乘數法檢驗ARCH效應。假設模型隨機誤差項εt～ARCH(q)建立輔助回歸方程：

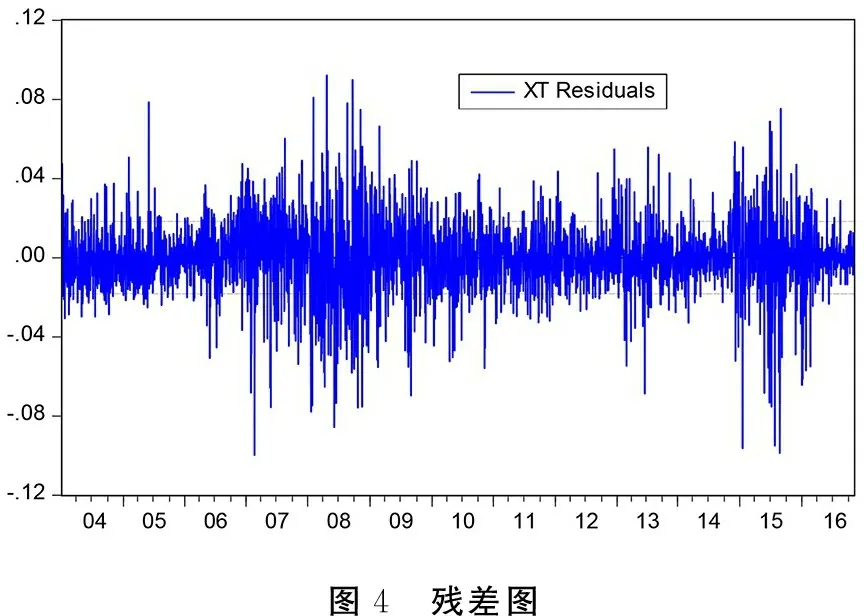
圖4 殘差圖

若檢驗的原假設H0=α1=α2=…=αq=0，則說明不存在ARCH效應，若回歸系數至少存在一個不為0，說明序列存在ARCH效應不接受原假設。檢驗統計量為LM=nR2～χ2(q)這里的n表示樣本個數，R2表示回歸系數。如果原假設被推翻則認為金融序列有ARCH效應，反之樣本序列不存在ARCH效應。其結果見表3。

由上面的分析可以看出最小二乘法的檢驗結果中的統計量Obs*R-squared的值及其概率，及統計量F的值及其概率，概率值都將近為零，由此認為金融序列存在ARCH效應。[4]

(三)建立GARCH模型對其進行參數估計

筆者將對3個模型進行參數估計，計算出標準差，由標準差得到VAR的值。

1.GARCH(1，1)的模型

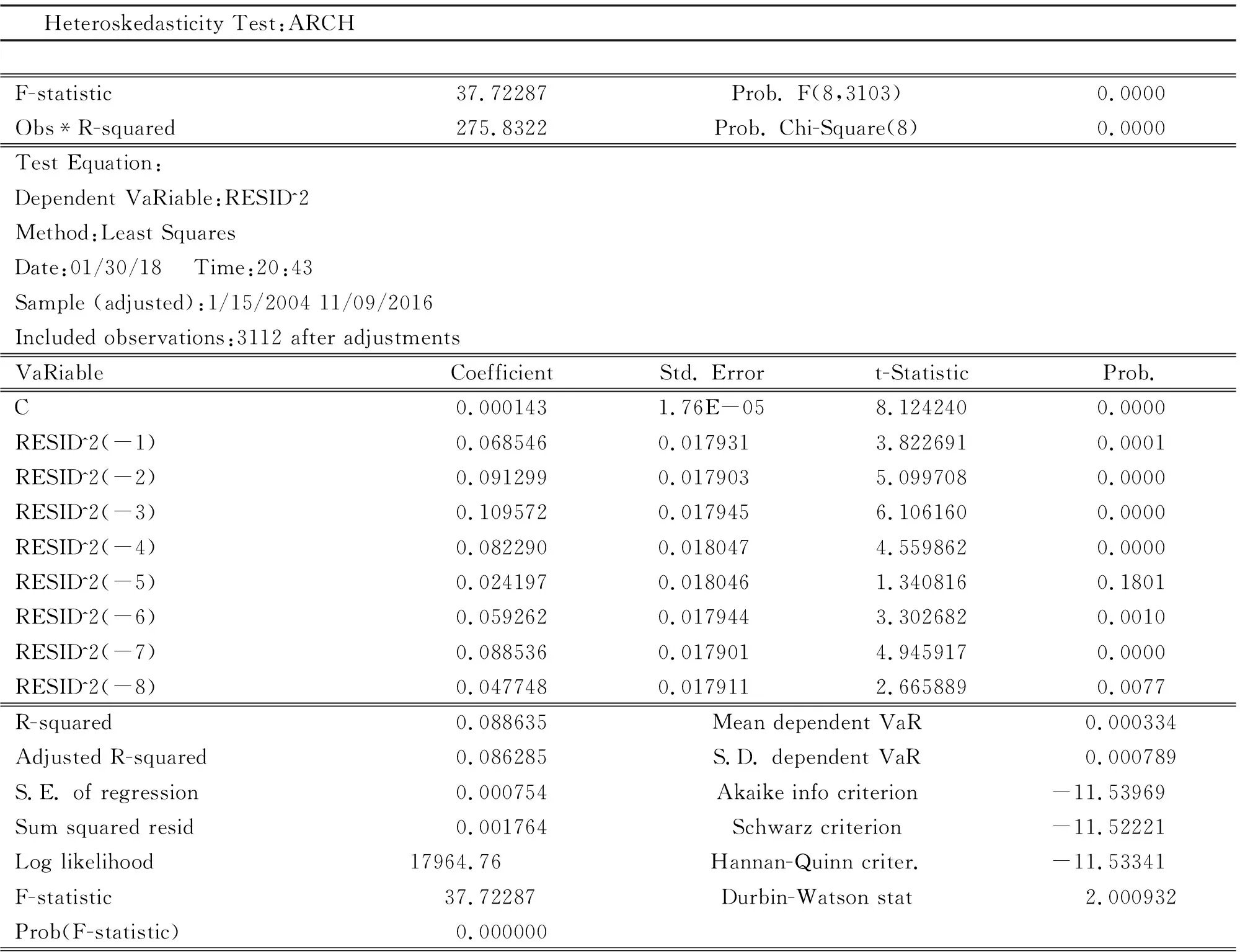
表3 ARCH-LM檢驗結果輸出

需要對這里的(α0α1γ1)進行參數估計。

2.EGARCH(1,1)的模型

需要對這里的(α0α1γ1β1)4個參數進行估計。

3.PGARH(1，1)的模型

需要對這里的(α0α1|1γ1δ)5個參數進行估計。

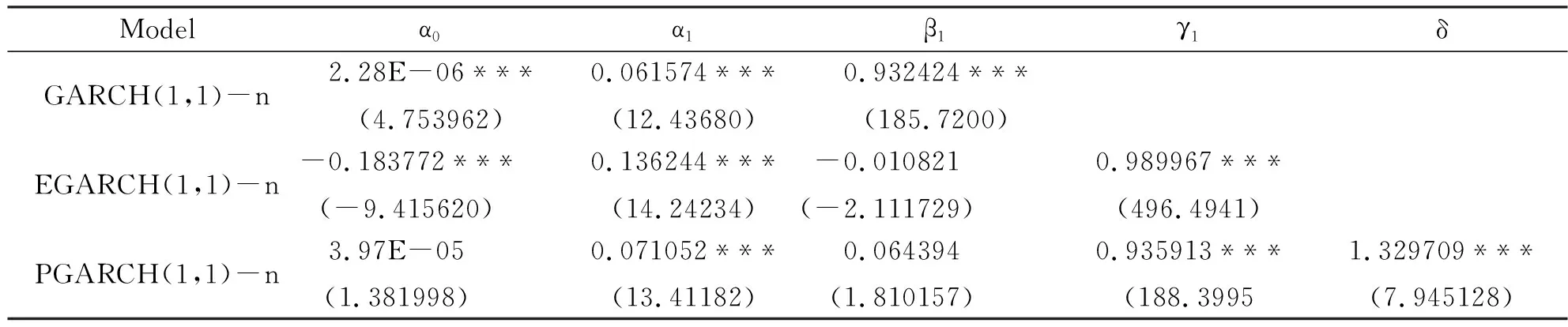
表4 正態分布假定下模型的參數估計

注：上述括號內的數字表示為t的估計統計量，***表示在1%的置信水平下顯著；**表示在5%的置信水平下顯著；*表示在10%的置信水平下顯著。

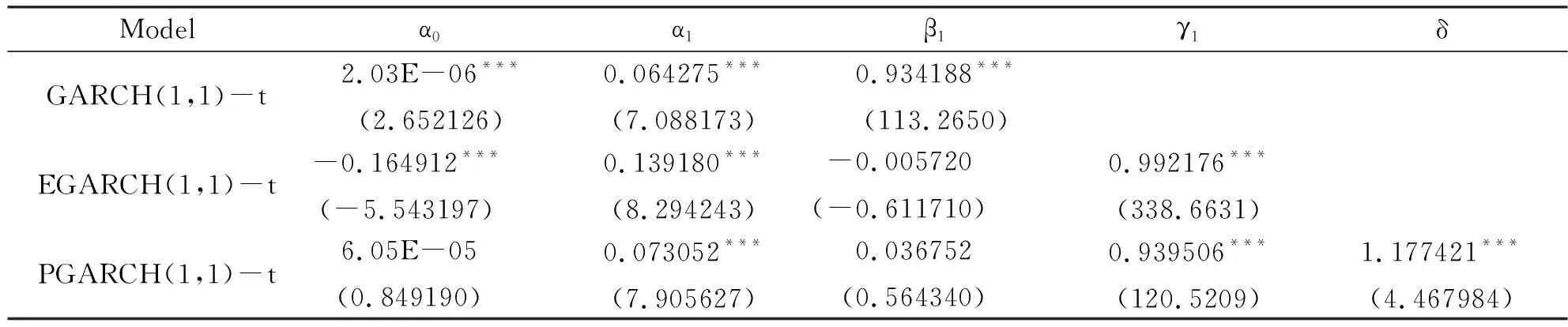
表5 在T分布的假定下模型的參數估計

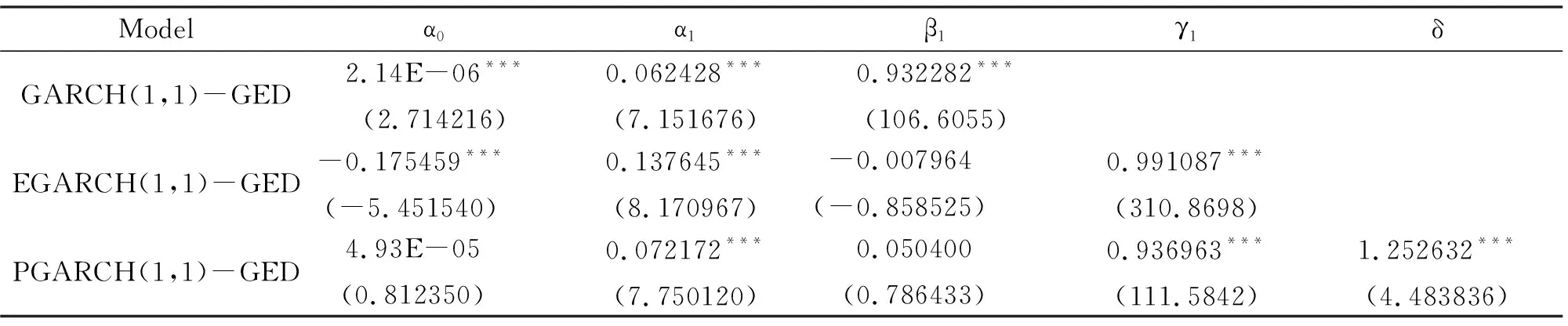
表6 在GED分布假定下模型的參數估計

上述表4、表5、表6是由Eviews得到的在正態分布、T分布、廣義誤差分布下的參數估計的結果，我們可以知道3個模型在1%的置信水平下都是比較顯著的，擬合的效果較好。在GARCH、EGARCH、PGARCH模型下γ都比零大，這在一定程度上說明有非對稱效應的存在，即不好的消息會比好的消息對市場產生更大的影響。根據檢驗可以發現3個模型的參數都是顯著的，而在對殘差項進行ARCH效應檢驗的時候，我們發現異方差現象不是很明顯，這說明了上述模型可以比較好地刻畫上證50的對數收益率的異方差現象。

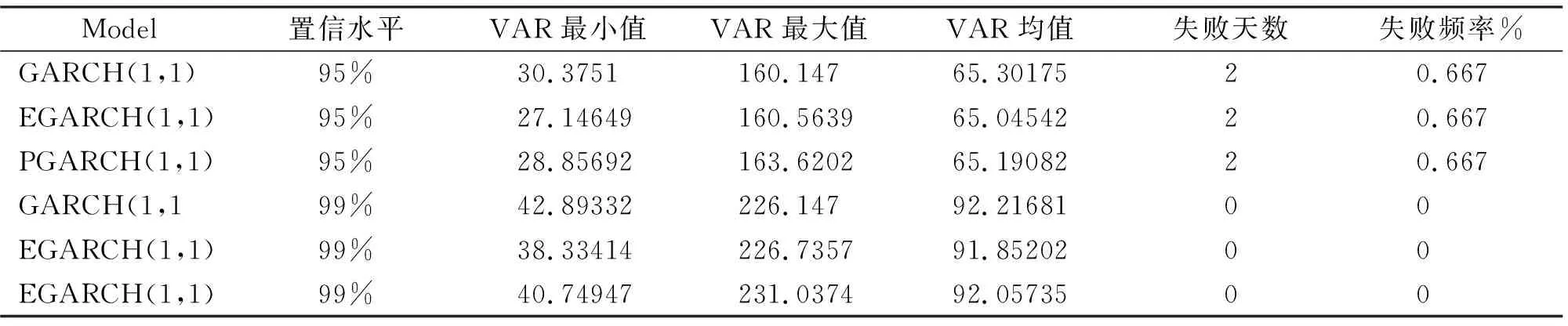
表7 正態分布下的VAR的計算結果

表8 T分布下VAR的計算結果

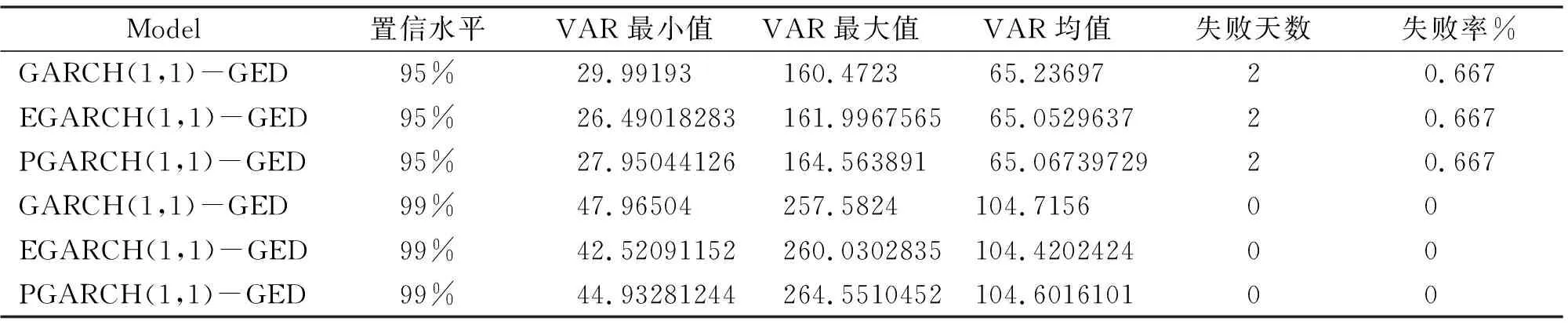
表9 廣義誤差分布下VAR的計算結果

(四)VAR的計算和回測檢驗

利用Eviews軟件得到金融序列的條件異方差，根據條件異方差算出標準差，然后將其帶入VaR的公式里面，我們可以得到在不同分布不同置信水平下的VaR值。計算出所有金融序列VAR值的平均值，根據計算的結果進行回測檢驗，一個簡單的做法就是向后構建一個檢驗樣本。比如樣本數為300天，根據2016年11月10日到2018年1月26日每日交易收盤價，逐日計算頭寸損益，并將計算結果按升序排列，即可得到一個關于損益的排序結果。然后把金融序列的VAR均值與頭寸損益的絕對值進行比較，如果VAR均值大于頭寸損益，說明檢驗失敗；如果VAR均值小于頭寸損益，說明檢驗成功。統計出失敗天數和失敗頻率就可以得到上面的3個表，即表5、表6、表7。

(五)模型的效果分析和比較

通過以上的3個計算VAR結果的表格，(見表7，表8,表9)我們可以看到上證50對數收益率在T分布下失敗天數和失敗率最小，這說明在T分布條件下，金融序列的尾部特征得到了較好的表現，但是在T分布下金融序列的VAR值高于正態分布和廣義誤差分布，從側面反映出其風險被高估，正態分布和廣義誤差分布的估計效果也不錯，失敗天數和失敗率一致。

綜上，可以發現在同一個分布條件下，GARCH模型、EGARCH模型、PGARCH模型的VAR值在同一個置信區間相差不大，在失敗率和失敗天數上正態分布和廣義誤差分布上基本一致，并且在正態分布和廣義誤差分布下VAR的值在相同的置信區間下，GARCH模型下的VAR值要高于EGARCH和PGARCH值，說明EGARCH模型和PGARCH模型的擬合效果比GARCH模型的擬合效果要好。這同時證明上證50指數存在顯著的杠桿效應，不好信息給股市帶來影響力比好的信息給股市帶來的影響力還要大。

四、結論

第一，上證50對數收益率呈現出左偏，尖峰后尾的特點，并且有強烈的波動聚集，存在自回歸的條件異方差，從檢驗結果可以看出歷史的波動對將來的波動變化的影響變得逐漸減小。

第二，上證50的收益率序列存在比較顯著的杠桿效應，也就是在相同的條件下，股市中的利空消息給市場帶來的影響比利好消息帶來的影響更大，也就是所謂的非對稱效應。

第三，我們根據GARCH模型族對金融序列進行一系列的檢驗，得到了在正態分布、T分布以及廣義誤差分布下的參數，由參數可以得到模型在99%的置信區間內比較顯著，從整體上來說正態分布的結果較為保守，而T分布和廣義誤差分布的效果要略勝一籌。