對一道向量題的認識與思考

摘 要:數學離不開解題,教師應立足課標,研究教學,把控好題目難度,甄選好題,讓學生學習更加高效而非陷入題海。
關鍵詞:平面向量;解題教學;好題
除了利用坐標把向量問題代數化,借助基底來進行向量的計算也是通性通法。從以上解法可以發現,善于利用A,B的關系大大簡化了該題的計算。讓學生在做中學,學中做,最優解法在反思中生成,解題能力在實戰中獲得提升。
三、 感悟反思
(一) 關于高考中的平面向量
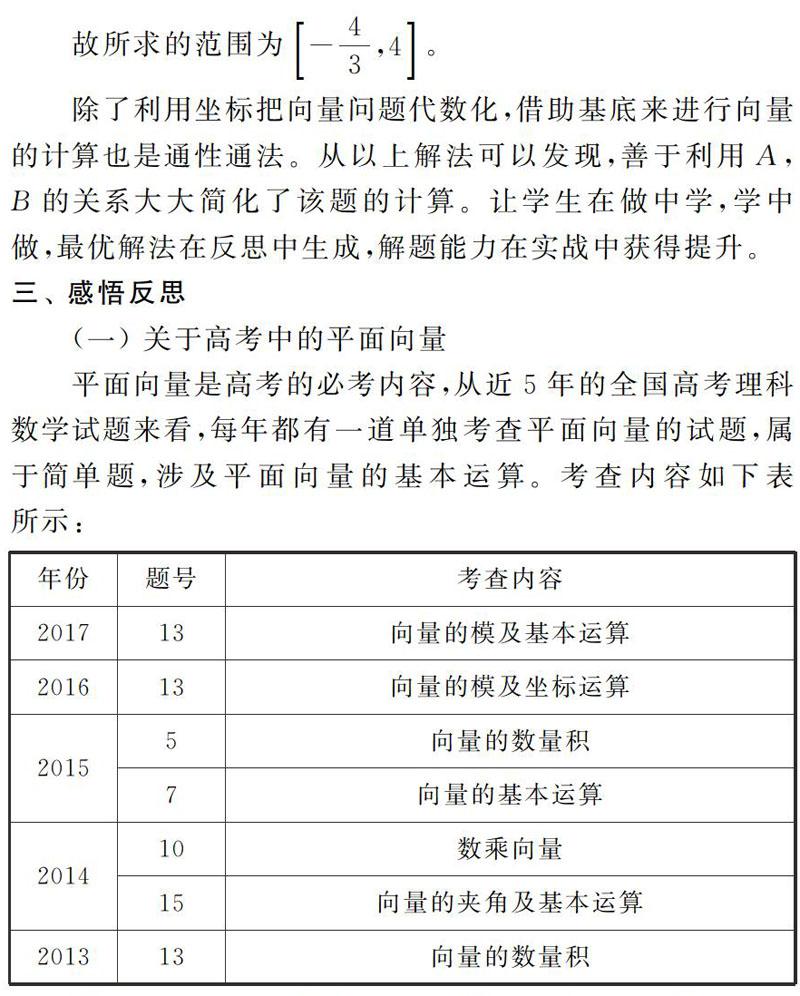
平面向量是高考的必考內容,從近5年的全國高考理科數學試題來看,每年都有一道單獨考查平面向量的試題,屬于簡單題,涉及平面向量的基本運算。考查內容如下表所示:
年份題號考查內容201713向量的模及基本運算201613向量的模及坐標運算
20155向量的數量積7向量的基本運算
201410數乘向量15向量的夾角及基本運算
201313向量的數量積
向量既是幾何研究對象,也是代數研究對象,是溝通幾何與代數的橋梁。雖然平面向量可以跟很多主干內容相結合,但是就目前對平面向量的考查來看,主要是基本計算,所以沒必要加大平面向量的練習難度,增加學生的負擔。
涉及平面向量的試題一般采用坐標法或轉化為基底計算,注重通性通法,不要盲目尋求特殊技巧。
(二) 關于解題教學
學好數學離不開解題,但是解題不意味著沉迷題海盲目刷題。教師要減少重復的、低效的、機械的練習,增加能夠調動學生積極思維的、具有挑戰性的教育教學活動,提高解題訓練的質量。要提高解題訓練的質量,減負增效的前提條件是教師要注重題目的篩選,甄選好題。章建躍博士曾說過,從數學角度衡量,“好題”應具有以下“品質”:與重要的數學概念和性質相關,體現基礎知識的聯系性,解題方法自然、多樣,具有自我生長的能力等;從培養思維能力的角度,則應有:問題是自然的,對學生的智力有適度的挑戰性,題意明確、不糾纏于細枝末節,表述形式簡潔、流暢、好懂等。
本文列舉的題目題干簡潔明了,看似平實實則包含了豐富的知識與方法,除了題目中直接呈現出的平面向量數量積的取值范圍問題,還涉及平面向量的基本運算、二次多項式的最值問題,特值法、配方法、數形結合、化歸轉化等思想方法,是學生高三綜合練習的好題。
作者簡介:
洪揚婷,福建省泉州市,泉州市第九中學。

