甲酸乙酯-乙醇二元體系等壓汽液相平衡研究

張棋茜，蔣文偉，羅 芩，楊 琴

(1.四川大學 化學工程學院，四川 成都 610065； 2.成都惠恩精細化工有限責任公司，四川 成都 610041)

甲酸乙酯是重要的化工基礎原料之一，具有十分廣闊的應用.甲酸乙酯可以作為硝酸纖維素和醋酸纖維素的優良溶劑，同時也作為有機合成的中間體被用在醫藥生產上.此外，甲酸乙酯還應用于配制食品、香煙、谷類、香精[1].

目前，甲酸乙酯的合成方法主要是甲酸和乙醇在硫酸作為催化劑存在下加熱進行酯化反應.由于甲酸乙酯不穩定，容易發生水解，因此酯化反應過程是一個可逆過程.為了提高產率，通常采用乙醇過量的方法，這就需要采用精餾技術對甲酸乙酯進行分離提純[2].因此，研究甲酸乙酯-乙醇體系的汽液相平衡數據對于甲酸乙酯的分離工藝設計及優化有著重大意義.文獻[3]只提供了甲酸乙酯和乙醇體系的共沸溫度，張士旭等[4]利用修正的UNIFAC模型對甲酸乙酯和乙醇進行了常壓(101.325 kPa)下的汽液相估算，但是目前甲酸乙酯-乙醇體系的相關汽液相平衡實驗數據還相當缺乏.針對該研究現狀，本文對甲酸乙酯-乙醇體系的汽液相平衡進行研究，獲得準確可靠的汽液相平衡數據及相關模型參數，為甲酸乙酯-乙醇體系的精餾分離過程提供數據基礎.

1 實驗部分

1.1 實驗儀器及試劑

實驗儀器：上海精科GC122氣相色譜儀，FID檢測器；N2000色譜工作站，浙江大學智達信息工程有限公司；改進的ROSE汽液平衡釜，成都凌云玻璃儀器廠加工；精密溫度計(50～100 ℃，精度為0.1 ℃).

實驗試劑：無水乙醇，分析純，成都科龍化工試劑廠；甲酸乙酯，分析純，成都科龍化工試劑廠；正丙醇，分析純，成都科龍化工試劑廠.

1.2 實驗分析方法

用GC122氣相色譜儀對甲酸乙酯-乙醇樣品進行分析.分析條件：氫離子火焰檢測器(FID)，色譜柱為SE-30型石英毛細管柱，柱長30 m，直徑0.32 mm；膜厚1 μm，分流比100∶1，進樣量為0.2 μL；柱溫40 ℃，氣化室溫度120 ℃，檢測器溫度120 ℃.樣品測定采用內標法，在選定的氣象色譜條件下分析樣品，以正丙醇為內標物，測得甲酸乙酯與正丙醇的面積比(Ai/As)，然后作出Ai/As-mi/ms工作曲線，如圖1所示.

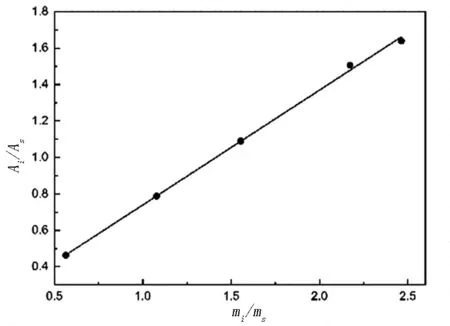
圖1 甲酸乙酯校正因子圖Fig.1 Ethyl formate correction factor

該工作曲線的方程為：

y=0.6303x+0.1062(R2=0.994{

1.3 實驗裝置的校核

為了驗證實驗裝置測定出的汽液相平衡數據的可靠性，用乙醇-水體系對平衡釜進行校核.精確配置不同濃度的乙醇-水混合溶液，用阿貝折光儀測定各乙醇-水溶液樣品的折光率，繪制出標準曲線.如圖2所示.

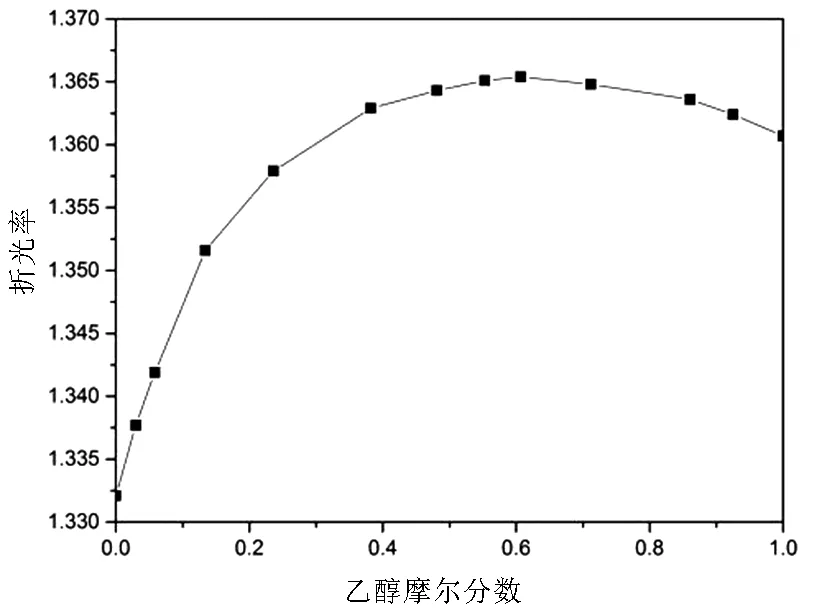
圖2 25 ℃時乙醇-水折光率曲線圖Fig.2 The refractive index curve of Ethanol-Water at 25 ℃

由圖2可以看出，乙醇-水體系折光率在乙醇摩爾分數小于0.5之前有規律上升，0.5之后緩慢下降.分段擬合出折光率曲線方程為：

x≤0.5；y=-0.187x2+0.150 3x+

1.333 2(R2=0.993 3)

x>0.5；y=-0.031 3x2+0.038 8x+

1.353 2(R2=0.994 2)

上式中：x為乙醇摩爾分數，y為折光率.

為了與文獻值[5]進行對比，選定于100 kPa下對乙醇-水體系進行汽液相平衡數據的測定，結果如圖3所示.實驗結果與文獻值較為吻合，表明了此平衡釜對測定汽液平衡數據的可靠性.

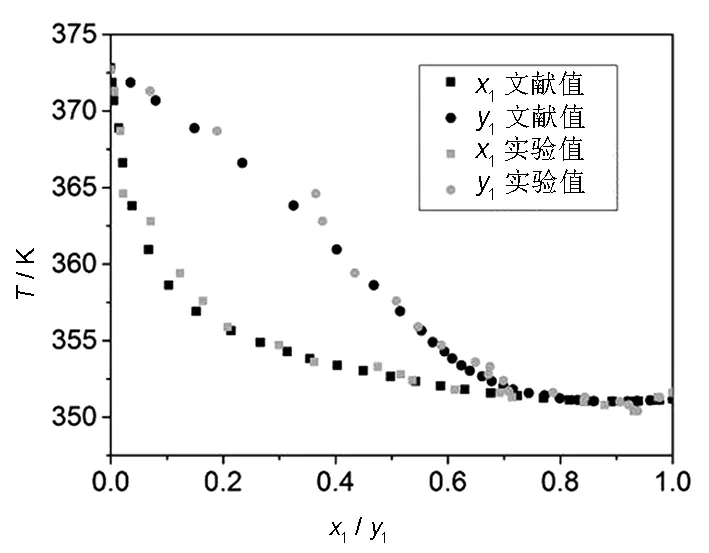
圖3 乙醇-水體系100 kPa汽液平衡數據實驗值與文獻值對比Fig.3 Comparison of VLE data of ethanol-water at 100 kPa from experiments and literature

1.4 實驗數據的測定

對實驗裝置進行氣密性檢測，保證實驗裝置具有良好的氣密性，并根據當時實驗室內的氣壓計算出對應系統補償壓力.通過電接點壓力自動調節器對壓力進行補償，使體系始終保持恒壓.將配置好的甲酸乙酯-乙醇溶液加入到干燥的平衡釜內，接通冷卻水，打開水浴鍋.將溫度調控到比共沸溫度略低一點的溫度值，緩慢加熱，觀察釜內狀態、和冷凝管的冷凝狀態.在沒有冷凝液滴生成的情況下，緩慢提高水浴溫度，當釜內溶液開始沸騰時，冷凝管開始緩慢出現液滴時，打開回流閥門，讓冷凝液回流液充分循環.當溫度維持穩定不變，且冷凝液流穩定，溫度與壓力保持5 min甚至更長時間不變，認為汽液相平衡已經建立.記錄下平衡溫度，同時提取液相口和汽相口液體樣.立即用氣相色譜儀進行組分分析，每個樣品分析3次，求取平均值.

2 結果與討論

2.1 測定結果

實驗所測定的甲酸乙酯-乙醇相平衡數據見表1.

表1 95.8 kPa下甲酸乙酯(1)-乙醇(2)二元體系的平衡數據與關聯結果
Tab.1 VLE data and the regressive results of ethyl formate(1)-ethanol(2) at 95.8 kPa

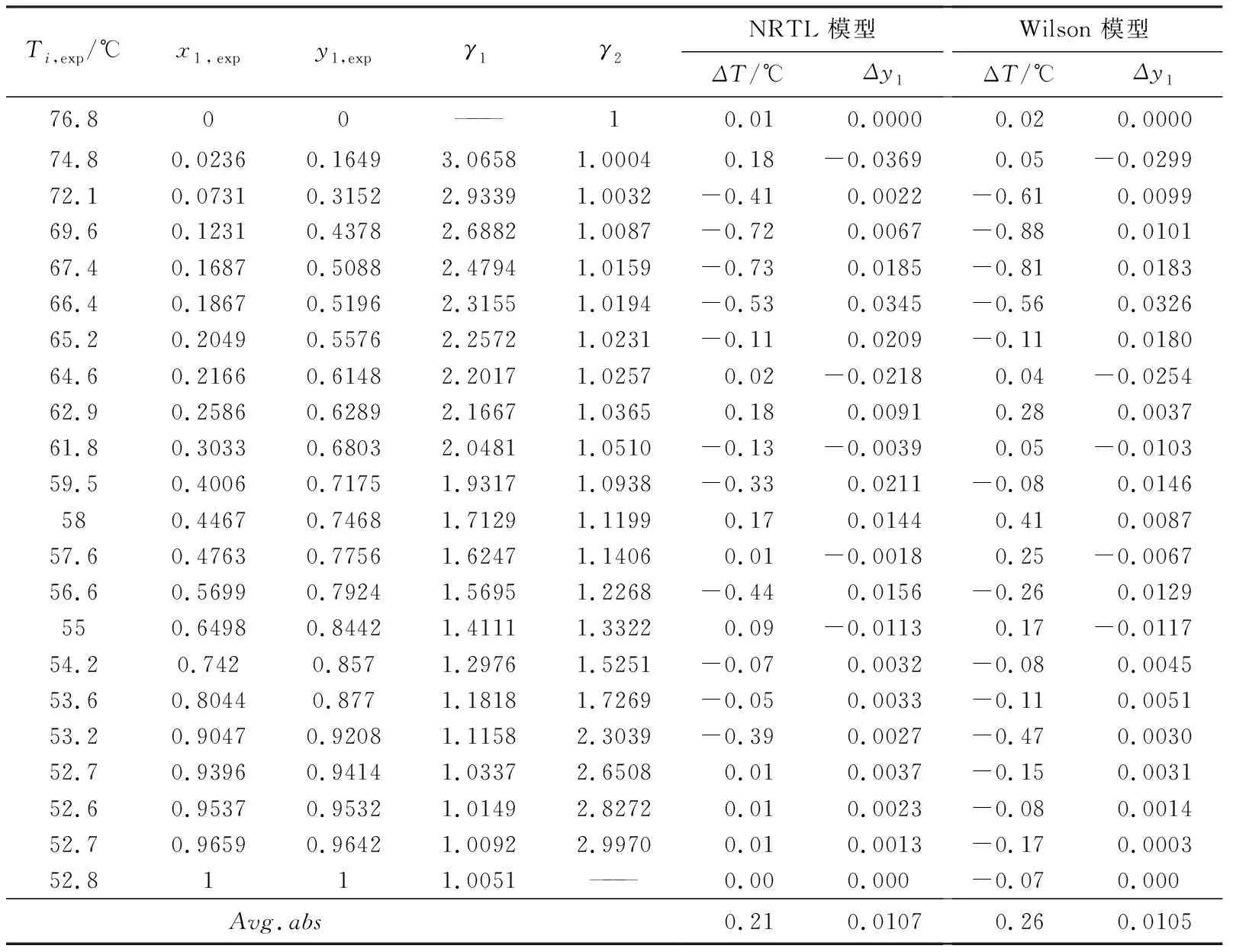
Ti,exp/℃x1,expy1,expγ1γ2NRTL 模型Wilson 模型ΔT/℃Δy1ΔT/℃Δy176.800———10.010.00000.020.000074.80.02360.16493.06581.00040.18-0.03690.05-0.029972.10.07310.31522.93391.0032-0.410.0022-0.610.009969.60.12310.43782.68821.0087-0.720.0067-0.880.010167.40.16870.50882.47941.0159-0.730.0185-0.810.018366.40.18670.51962.31551.0194-0.530.0345-0.560.032665.20.20490.55762.25721.0231-0.110.0209-0.110.018064.60.21660.61482.20171.02570.02-0.02180.04-0.025462.90.25860.62892.16671.03650.180.00910.280.003761.80.30330.68032.04811.0510-0.13-0.00390.05-0.010359.50.40060.71751.93171.0938-0.330.0211-0.080.0146580.44670.74681.71291.11990.170.01440.410.008757.60.47630.77561.62471.14060.01-0.00180.25-0.006756.60.56990.79241.56951.2268-0.440.0156-0.260.0129550.64980.84421.41111.33220.09-0.01130.17-0.011754.20.7420.8571.29761.5251-0.070.0032-0.080.004553.60.80440.8771.18181.7269-0.050.0033-0.110.005153.20.90470.92081.11582.3039-0.390.0027-0.470.003052.70.93960.94141.03372.65080.010.0037-0.150.003152.60.95370.95321.01492.82720.010.0023-0.080.001452.70.96590.96421.00922.99700.010.0013-0.170.000352.8111.0051———0.000.000-0.070.000Avg.abs0.210.01070.260.0105

注：ΔT=Tcal-Texp；Δy=ycal-yexp；Tcal為熱力學模型計算的溫度值，Texp為實驗測定的溫度值；ycal為熱力學模型計算的甲酸乙酯汽相質量分數，ycal為實驗測定的甲酸乙酯汽相質量分數.

在95.8kPa條件下，屬于低壓范圍，可以將甲酸乙酯體系氣相視為理想氣體.汽液相平衡公式簡化為[6-7]

(1)

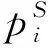
甲酸乙酯、乙醇飽和蒸汽壓用Antoine方程計算：

(2)

甲酸乙酯和乙醇的Antoine常數[7-8]在表2給出.

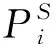
表2Antoine方程參數值Tab.2ParametersofAntoineequation

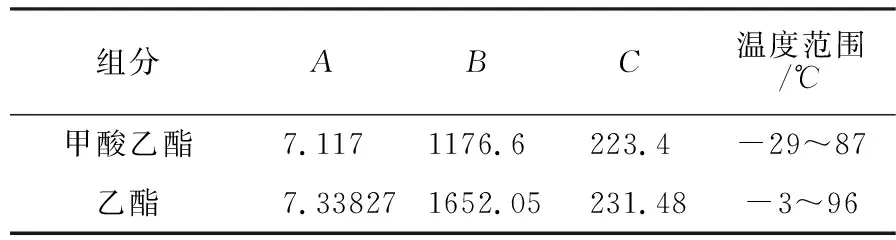
組分ABC溫度范圍/℃甲酸乙酯7.1171176.6223.4-29～87乙酯7.338271652.05231.48-3～96

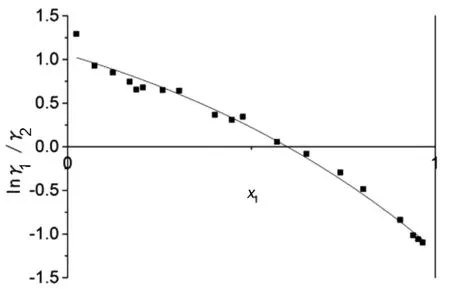
圖4 lnγ1/γ2 -x1 曲線圖Fig.4 Curve of lnγ1/γ2 -x1

2.2 熱力學一致性檢驗

實驗測得數據是否可靠，可從其是否符合熱力學一致性來檢驗，基本依據是Gibbs-Duhem方程[7].對于二元恒壓體系，G-D方程為

(3)

其中：HE為二元體系的超額焓，R為通用氣體常數.對恒壓方程進行積分有

(4)

由于式(4)HE對于一般極性和非極性體系都不可以忽略，積分很難.所以對于二元恒壓的汽液相平衡，通常采用Herington的半經驗方法進行熱力學一致性檢測[9].

檢驗方法如下：以lnγ1/γ2對于x1作圖，計算出

D=|(SA-SB{/(SA+SB{|×100

(5)

再計算出

(6)

式中SA，SB分別是曲線與橫坐標上下的面積代數和，Tmax，Tmin分別為2組分的沸點.判斷標準為：若D-J<10，則認為數據符合熱力學一致性.用Herington面積檢驗法對所測得的甲酸乙酯-乙醇二元體系在95.8KPa下的汽液相平衡數據進行熱力學一致性檢驗，如圖4所示.計算結果D-J=8.1595<10，表明數據通過熱力學一致性檢驗.

2.3 汽液平衡數據的關聯

用AspenPlusV8.4軟件對所測得的汽液相平衡數據進行關聯，回歸出Wilson模型[10]和NRTL[11]模型的aij,aji,bij,bji參數.Aspen中的Wilson模型和NRTL模型的參數表達形式相比于普遍文獻有所改動[12].具體如下：

Wilson模型：

(7)

lnΛij=aij+bij/T+cijlnT+dijT

(8)

其中：aij≠aji，bij≠bji，cij≠cji，dij≠dji.

NRTL模型：

(9)

Gij=exp(-αijτij{

(10)

τij=aij+bij/T+eijlnT+fijT

(11)

αij=cij+dij(T-273.15)

(12)

其中：τ=0，G=1，α=0.3；aij≠aji，bij≠bji，cij≠cji，dij≠dji.

NRTL模型的非隨機參數αij在Aspen的NRTL模型中是通過cij表示.根據文獻[13]分類，選擇NRTL模型的非隨機參數cij為0.3.

經過回歸計算，得出各模型的參數見表3.

表3Wilson和NRTL模型參數Tab.3ParametersoftheWilsonandNRTLmodels

模型a12a21b12b21NRTL1.257260.639002-99.0678-115.423Wilson-8.045349.673072497.34-3464.62

實驗測得的汽液相平衡數據與Wilson模型和NRTL模型關聯后計算的數據見表1，擬合出的T-x-y相圖如圖5、圖6所示.Wilson模型和NRTL模型關聯計算出的平均溫度絕對偏差分別為0.25 ℃和0.21 ℃；汽相組成平均絕對偏差分別為0.0105和0.0107.結果表明，實驗測得數據與Wilson、NRTL模型關聯的數據吻合度較好，實驗數據是可靠的.

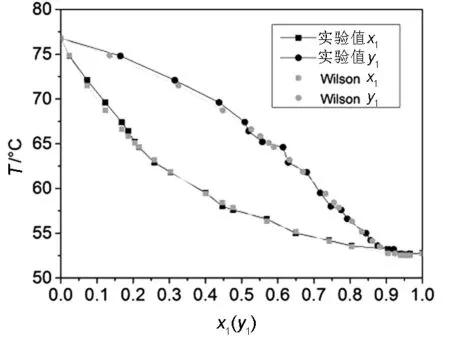
圖5 甲酸乙酯(1)+乙醇(2) T-x-y 圖(Wilson模型)Fig.5 T-x-y plot of the ethyl formate(1)+ethanol(2) System (Wison model)

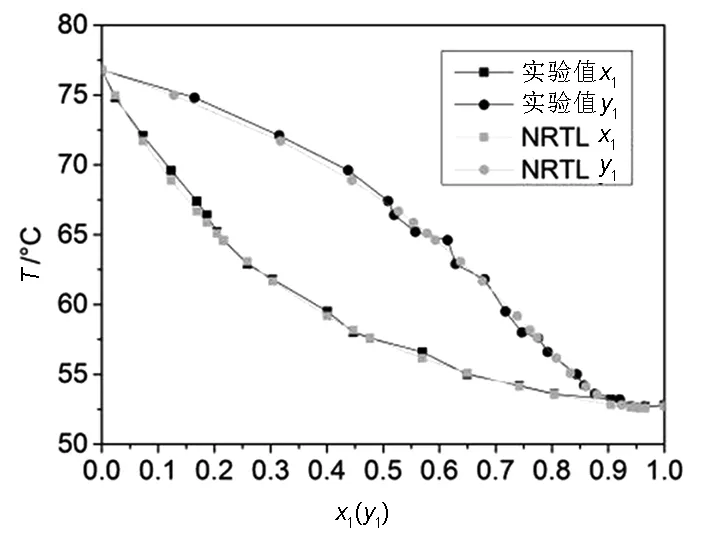
圖6 甲酸乙酯(1)+乙醇(2) T-x-y 圖(NRTL模型)Fig.6 T-x-y plot of the ethyl formate(1)+ethanol(2) System (NRTL model)

3 結論

(1)用改進的汽液相平衡釜測定了95.8kPa壓力下的甲酸乙酯-乙醇體系的汽液相平衡數據，數據通過了熱力學一致性檢驗.

(2)用Wilson模型和NRTL模型對所測的實驗數據進行了關聯，模型預測出的結果數據與實驗測得的數據能較好的吻合，滿足了精度要求，為甲酸乙酯-乙醇體系的分離過程提供了可靠的熱力學基礎數據.