傳播源估計中有效觀察點部署策略研究

劉 棟，趙 婧，聶 豪

(1. 河南師范大學 計算機與信息工程學院，河南 新鄉 453007; 2. 教學資源與教育質量評估大數據河南省工程實驗室，河南 新鄉 453007)

0 引言

伴隨著Facebook、微信等在線社交網絡服務的出現，社交網絡已經成為當今社會人們信息交流的重要渠道和載體，且這些社交網絡允許用戶建立自己的“媒體”，對外發布、傳播信息。可靠的信息能夠給人們的生活帶來便捷，但謠言在互聯網上的傳播所帶來的負面影響也不可估量。傳染病的傳播也可看作網絡上的傳播現象，如2009年由流感病毒新型變體甲型H1N1流感所引發的全球性流行病疫情[1]，在很短時間內便蔓延全球。

謠言或疾病的傳播都是依賴于具體網絡而存在的。例如，謠言傳播依賴于社交網絡，疾病傳播則依賴于人際交互網絡。這些網絡一般具有規模大，節點之間的聯系復雜等特征。在此類網絡上，如何快速準確地確定疾病的傳染源、謠言的源頭就顯得十分重要。如果在短時間內確定出疾病的傳染源，就能夠更好地控制整個疾病的傳播，縮小其傳播范圍，減少傳染病對人們生命安全的威脅。如果能在散布謠言后的關鍵時期迅速定位謠言來源，就能減少謠言對政治、人類切身利益和社會穩定的負面影響。因此，在這個背景下，如何在一個網絡上定位一個傳染源或者謠言的源頭就成為一件非常有意義且十分具有挑戰性的事情。

對于網絡上的源點定位問題，一種較為樸素的方法是通過獲取網絡中每個節點在網絡傳播中的狀態，根據其相關記錄，確定信息傳播的源點。雖然這種方法能夠準確定位信息源，但成本極高，可行性差，對于大規模網絡來說幾乎無法實施。因此，需要一種有效可行的方法來估計和預測信息源的準確位置。最新的研究趨勢是通過在網絡中部署少量觀察點，根據其接收的節點信息，推斷出信息源點在網絡中的位置。在該任務下，如何有效地部署觀察點，從而提高傳播源定位精度，成為了亟待解決的關鍵問題。本工作針對上述問題展開研究，力圖揭示網絡中觀察點部署策略與源點估算精度的關系。

本工作提出了幾種觀察點部署策略，包括隨機、度、聚類系數、特征向量、緊密度和介數。并且采用SI傳播模型和反向貪心溯源算法在合成網絡和真實網絡中進行模擬仿真。通過分析不同觀察點部署策略對于傳播源定位精度的影響，期望尋找到有效的觀察點部署策略。

1 相關研究

目前，估計傳播源在傳染病控制、輿情控制等方面的應用越來越廣泛，國內外研究人員對于估計傳播源相關問題的研究也越來越深入。根據快照信息范圍可以分為完整節點信息定位和部分節點信息定位。其中有的是關于定位傳染病的源頭、有的是關于定位謠言的源頭等等，但根據快照信息范圍大致可以歸為以上兩類。

Shah等人[2]針對正則樹上的SI模型提出一個基于傳播中心性的極大似然估計算法來確定傳播源。Fioriti等人[3]提出了計算感染圖中每個節點的動態年齡的溯源算法DA。Comin等人[4]在雪崩傳播模型下提出了無偏中介算法。Prakash等人[5]提出了基于最小描述長度的NetSleuth算法解決溯源問題。還有Nino Antulov-Fantulin 等人[6]提出了基于蒙特卡洛模擬的定位算法。

以上工作都需要明確所有節點的傳播狀態，在大型網絡中這將要消耗很大的成本。為了克服這些困難，Pinto[7]設計了一個基于少量觀察點的精細極大似然估計算法來定位傳播源。Shen等人[8]開發了基于壓縮感知的構建方法并提出了一種基于觀察點反向傳播的一種定位條件[9]。Luo等人[10]提出了一種適用于一般網絡的反向貪心算法。這些方法的基本思想都是基于選擇的部分節點進行傳播源的估計。定位傳播源的精度在很大程度上取決于觀察點的選擇。

近幾年來國內外研究人員在觀察點部署策略上也取得了一定的進展。Brunella Spinelli等人[11]提出了一種在線迭代的部署最佳觀察點的方法來定位傳播源。Brunella Spinelli等人[12]還提出了基于傳播延遲方差的最大值和最小值來部署觀察點的方法。Celis等人[13]提出基于雙重解決集的部署觀察點策略。張錫哲等人[14-17]基于Pinto的極大似然估計溯源算法提出的一系列觀察點部署策略。上述研究均未基于反向貪心溯源算法提出觀察點部署策略。

其中，張錫哲等人[17]分析了基于節點中心性的觀察點部署策略對定位傳播源的精度的影響，他們的研究結果表明基于節點中心性的觀察點部署策略對于估計傳播源的精度并無顯著影響。與他們的研究結果不同的是，本工作同樣采用基于節點中心性的觀察點部署策略，但仿真結果表明采用特征向量的觀察點部署策略更有利于提高傳播源估計的精度。

分析與張錫哲等人研究的不同之處，主要在于他們的工作采用了基于少量觀測節點的極大似然估計算法定位傳播源，而本工作采用了基于傳播路徑的反向貪心算法。因此，估計傳播源的溯源算法也是關系到基于節點中心性觀察點部署策略適用性的重要因素。

本工作中，首先利用SI傳播模型模擬傳播。然后，根據傳播信息利用反向貪心算法定位傳播源，本文將在第二節中介紹所采用的傳播模型和定位方法。我們的主要工作是在模擬傳播完成后，提出了基于節點中心性的觀察點部署策略，根據各種策略選擇的部分觀察點進行傳播源定位，本文將在第三節介紹基于節點中心性的觀察點部署策略。第四節介紹實驗部分，最后在第五節做出結論。

2 所采用的傳播模型與定位方法

2.1 SI傳播模型

網絡可建模為一個無向圖G=(V,E)。其中V是頂點或節點的集合，E是邊的集合，代表兩節點之間有聯系。在本工作中，假設在圖G中最開始只有一個節點被“感染”，這個節點開始向它的鄰居節點傳播。本工作就是利用網絡中部分感染節點信息來確定這個傳播源。

在人群中的疾病傳播模型已經在文獻[18-20]中得到廣泛的研究，這些模型也被用來模擬在線社交網絡中信息的傳播[21-24]。SI模型是作為模擬疾病傳播的一種自然現象出現的。在SI模型中，節點有三種狀態： 已感染狀態、易感染狀態和不易感染狀態。已感染節點將會感染其他節點并且一直保持被感染的狀態；易感染節點表示目前未被感染，但至少有一個鄰居節點被感染；不易感染的節點也是未被感染的節點但是它的鄰居都未被感染。類似于傳染性疾病的傳播，該模型也能描述謠言的傳播，在模型中的單個人可分為兩種類型： 第一類人是不知情者，他們對謠言是渾然不知的；第二類人是傳播者，他們是謠言的知情者，并且喜歡對謠言進行傳播。

本工作中,采用的SI模型的時間是被劃分了的離散時間段，在時間段t內節點u的狀態用隨機變量X(u,t)表示。在時間t=0時，假設只有一個節點v*∈V被感染，稱這個節點為傳播源。假設感染過程是一個在離散時間內概率測度為P的馬爾可夫過程，且假設在下一個時間段開始。一個易感染節點被感染的概率為p,其中p∈(0,1)。 假設每個易感染節點是否會被感染都是相互獨立的，且不易感染節點始終都不會被感染。

在這個SI模型中，任何與被感染節點相鄰的健康節點被感染的概率都相同，與被感染的鄰居數量無關。傳播一段時間后，在所有節點的狀態信息中，健康節點的狀態都能正確地顯示出來，但是被感染節點的狀態只有一部分能正確顯示，稱為顯式狀態，另一部分將與健康狀態混淆，稱為隱式狀態。當易感染節點u被感染并且為顯式狀態時用X(u,t)=e表示，并且被感染后為顯示狀態的節點集用Ve表示；當易感染節點u被感染并且為隱式狀態時用X(u,t)=i表示。

用qu表示節點u被感染后為顯式狀態的概率，假設節點被感染后是否為顯式狀態與其他節點是相互獨立的。對于所有節點u∈V,如果qu=1，那么該模型本質上會和文獻[25-26]中的一致；然而對于所有節點u∈V如果qu趨近于0，則大多數節點將會表現為未感染狀態。在這種情況下，估計傳播源將會變的十分困難，并且在實際中估計傳播源的精度將很低。直觀地說，對于所有節點u如果qu≥p，則將會在這個SI模型中觀察到更多的被感染后為顯式狀態的節點，有利于提高估計傳播源的精度。在本工作中提出一個較弱的假設，對于所有節點u∈V，假設qu滿足

當p>1/2時，對于任意節點u，假設中的qu需要滿足足夠大。這是因為在足夠長的一段時間內，大部分節點將會被感染，若被感染的節點大都為隱式狀態，那么將很難估計傳播源；另一方面，如果p≤1/2，那么假設將微不足道。此時，對于任意節點u，該模型允許qu=0或者1，當qu=1時，意味著將要觀察所有被感染的節點，這種情況類似于文獻[27]中的情況。故總結一個易感染節點的概率轉換圖如圖1 所示。

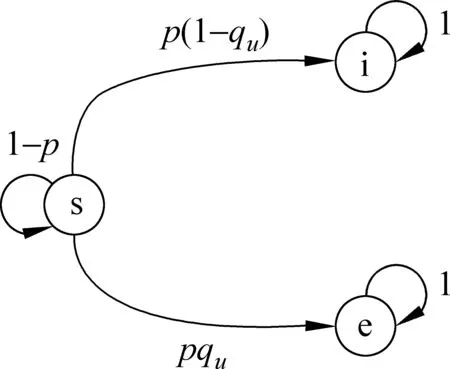
圖1 易感染節點的概率轉換圖

2.2 反向貪心溯源算法

本工作采用Luo等人[10]提出的方法估計傳播源。首先尋找與被感染節點集合一致的感染樹，然后計算可生成該感染樹的最可能傳播路徑，最后估計該樹的Jordan感染中心[28]作為網絡的傳播源。

在網絡G中，假設一個易感染節點只能隨機地被已感染鄰居節點中的一個節點感染，則在傳播源傳播結束后，被感染的節點組成的所有路徑將會是一個樹。經過傳播t時間后，任意一條感染路徑用Xt=X(u,τ):u∈V,1≤τ≤t表示，則由Xt形成的T(Xt)為G的一棵子樹。Tv表示以節點v為根節點的樹，則在G的所有子樹中肯定存在一個與被感染節點集合組成的感染樹一致的樹。Tv表示由已感染且為顯式狀態的節點Ve組成的感染樹的集合。假設節點v為源點，該傳播源的最可能感染路徑，如式(2)所示。

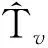
假設G為一般網絡，且v∈V是傳播源。那么，對于任意一個以v為根節點且由節點集合Ve組成的感染樹T有：

其中pa(u)表示節點u的父母節點，令

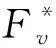
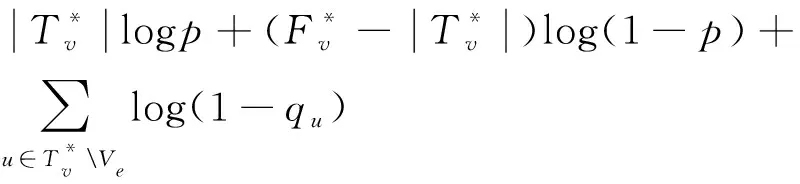
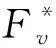
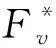
3 基于節點中心性的觀察點部署策略

在網絡G中，當傳播源利用SI傳播模型感染結束后，將得到為顯式狀態的節點集合Ve。在文獻[17]中，Luo等人是在隨機選擇部分節點上部署觀察點來收集信息。而本工作中，提出了基于節點中心性的觀察點部署策略，含節點的度、聚類系數、特征向量、緊密度、介數。下面介紹這五種指標信息。

(1) 度

用于描述在靜態網絡中節點產生的直接影響力，其值為與該節點直接相連的節點數。則度定義為式(7)。

其中，d(i)表示與節點i直接相連的節點數。

(2) 緊密度

用于描述網絡中的節點通過網絡到達其他節點的難易度，其值為該節點到其他所有節點的距離之 和的倒數。則緊密度定義為式(8)。

其中，dij表示節點i到節點j的最短距離。

(3) 介數

節點的介數反映了其在整個網絡中的作用和影響力，具有比較強的實際意義。則介數定義為式(9)。

其中，ljk表示節點j到節點k的最短路徑條數，ljk(i) 表示節點j與節點k之間經過點i的最短路徑條數。

(4) 聚類系數

在復雜網絡中，假設網絡中的一個節點i有ki條邊將它和其他節點相連，這ki個節點就稱為節點i的鄰居。由于在這ki個節點之間最多可能有ki(ki-1)/2條邊，而這ki個節點之間實際存在的邊數Ei和總的可能的邊數ki(ki-1)/2之比就定義為節點i的聚類系數Ccl(i)，Ei為這ki個節點之間實際存在的邊數總和即

聚類系數用于描述節點鄰居之間連接的緊密程度。整個網絡的聚類系數Ccl就是所有節點i的聚類系數Ccl(i)的平均值。顯然0≤Ccl≤1，當且僅當所有節點都為孤立節點，即沒有任何連接邊的情況下Ccl=0；當網絡是全局耦合時，即網絡中任意兩個節點都直接相連此時Ccl=1。

(5) 特征向量

用于描述節點周圍鄰居節點的重要性對該節點產生的影響。若λ為網絡鄰接矩陣A的主特征值，e=(e1,e2,...,en)為矩陣A對應于主特征值λ的特征向量，則特征向量定義，如式(11)所示。

從上面可以看出度、聚類系數、特征向量、緊密度以及介數這些指標信息，在網絡結構中的意義差別還是很大的。有的指標信息反映節點在整個網絡中的地位，有的指標信息揭示周圍鄰居對中心節點的影響等。這些差別在信息擴散的過程中都有所體現，在傳播過程都發揮了各自不同的作用，這也使得這幾類節點成為網絡中的重點研究對象。同時，正是這種在傳播時所表現出來的差異，顯得有必要按照這幾種指標信息選擇觀察點。因它們能從各自不同的方面揭示網絡中的信息傳播過程，能夠更全面地感知信息在網中的擴散，而這些對于準確定位網絡中的信息源來說是十分必要的。所以可利用以上指標信息作為選擇觀察點的標準。下面的工作通過實驗來分析這些部署策略對合成網絡和實際網絡的定位傳播源精度的影響。

4 實驗

4.1 實驗設置

本工作選取兩類網絡進行實驗。第一類是合成網絡，分別為從BA模型構造的無標度網絡、從WS模型構造的小世界網絡和從ER模型構造的隨機網絡；第二類為真實網絡，分別為屬于社會網絡的倉鼠網絡[29]，即在倉鼠網站中用戶的友誼與家庭之間的聯系網絡；屬于技術網絡的美國電力網絡[30]；屬于信息網絡的合著關系網絡[31]，選擇了其中最大連通子圖379個作者的關系網絡；屬于生物網絡的線蟲代謝網絡[32]。表1列出了這些網絡的規模。

本工作根據度、介數、緊密度、聚類系數以及特征向量五種網絡節點指標信息就可以產生五種觀察點部署策略。即在選擇觀察點之前，根據網絡節點指標信息的定義，計算網絡中每個節點的指標信息。之后將該指標進行從大到小排序，最后根據所需要的觀察點數量按照指標從大到小選擇節點作為觀察點。除此五種觀察點部署策略之外，還有一種就是隨機選擇節點作為觀察點，將此種部署策略作為與其他部署策略的對比。之后提到的觀察點部署策略也就是指的以上六種。

本工作中，設置選擇節點集Ve中50%的節點作為觀察點。如根據節點度大小來選擇50%的節點作為觀察點，則對網絡中所有節點按照度的大小排序，最后選擇排在前50%的節點作為觀察點。如果是在隨機選擇觀察點的情況下，就不需要排序，直接根據觀察點的數量在網絡中隨機選擇即可。

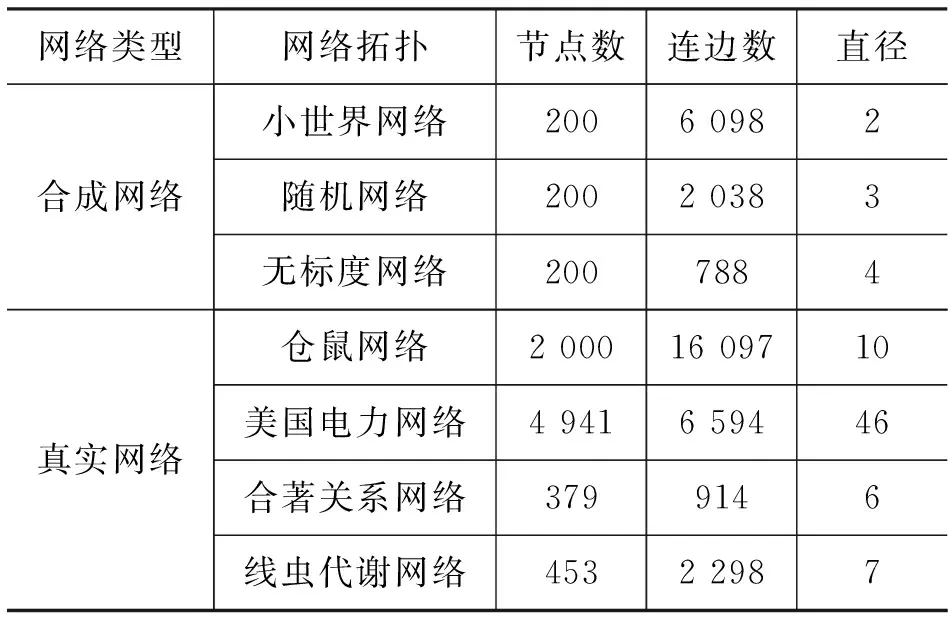
表1 實驗網絡的規模

在每種網絡上，仿真模擬運行1 000次。在每次模擬運行中，先隨機選擇一個節點作為傳播源，再使用SI模型模擬傳播。對于任意節點v，p和qv分別是在(0,1)和[max(0,2-1/p),1]中均勻選擇的。

4.2 實驗結果和分析

通過研究在合成網絡和真實網絡上估計傳播源精度的結果，探索了觀察點部署策略與估計傳播源精度的關系。從而發現觀察點部署策略對于估計傳播源精度產生的具體影響。

圖2是小世界網絡在各種觀察點部署策略下溯源算法的錯誤距離分布圖，錯誤距離是估計的傳播源與真實的傳播源之間的跳數。在觀察點部署策略隨機、度、聚類系數、介數、緊密度以及特征向量下估計傳播源的精度分別為0.23、0.12、0.24、0.21、0.25以及0.27。實驗結果表明采用特征向量觀察點部署策略估計傳播源的精度高于其他策略。

圖2 小世界網絡在各種觀察點部署策略下溯源算法的錯誤距離分布

圖3是隨機網絡在各種觀察點部署策略下溯源算法的錯誤距離分布圖。在觀察點部署策略隨機、度、聚類系數、介數、緊密度以及特征向量下估計傳播源的精度分別為0.03、0.01、0.02、0.01、0.02以及0.08。實驗結果表明采用特征向量觀察點部署策略估計傳播源的精度高于其他策略；另外，相比隨機選擇策略，采用特征向量觀察點部署策略，準確定位傳播源的精度可以提高到兩倍多。

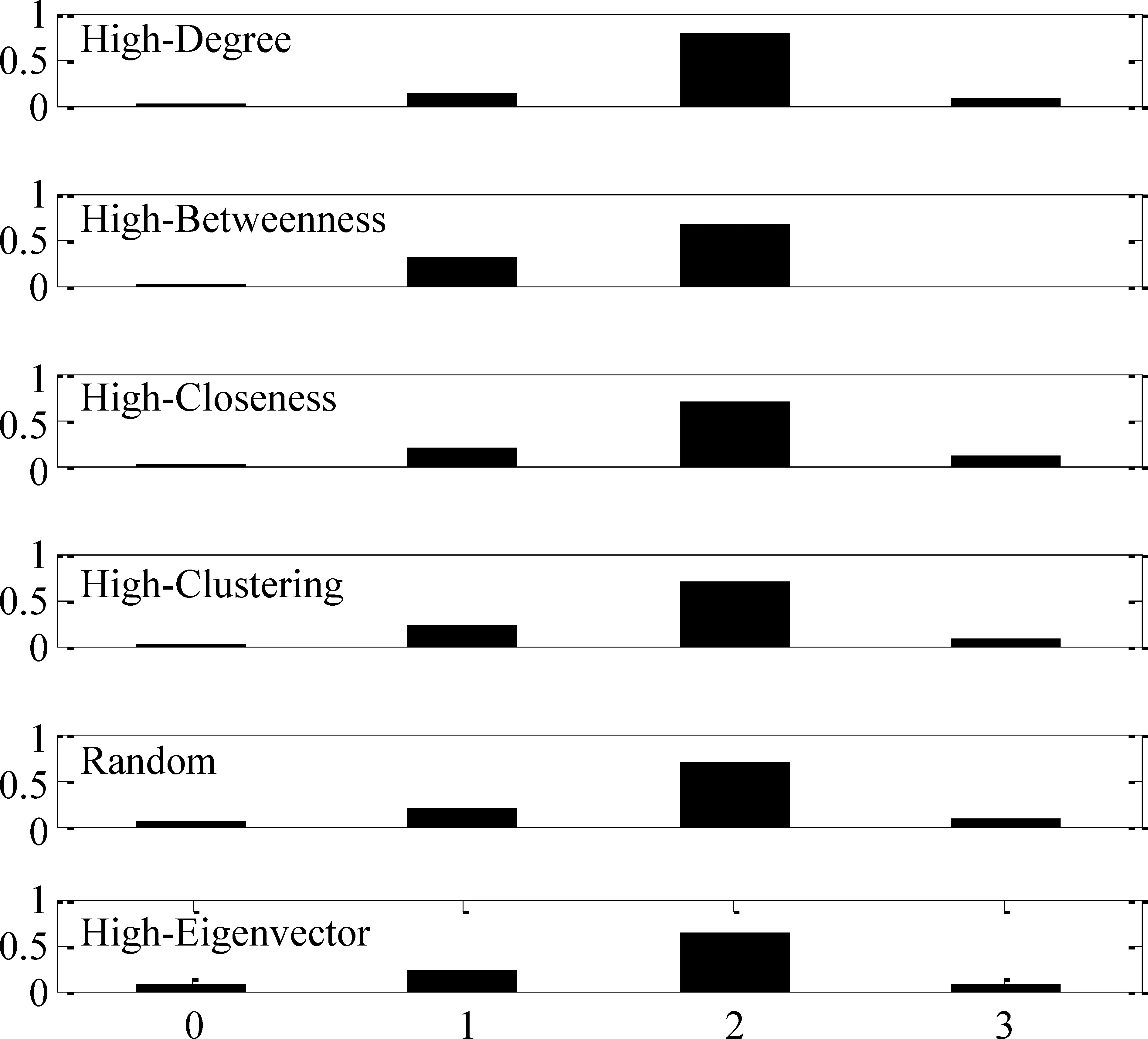
圖3 隨機網絡在各種觀察點部署策略下溯源算法的錯誤距離分布

圖4是無標度網絡在各種觀察點部署策略下溯源算法的錯誤距離分布圖。在觀察點部署策略隨機、度、聚類系數、介數、緊密度以及特征向量下估計傳播源的精度分別為0.10、0.21、0.05、0.15、0.21以及0.27。實驗結果表明，采用特征向量觀察點部署策略估計傳播源的精度高于其他策略；另外，相比隨機選擇策略，采用特征向量觀察點部署策略，準確定位傳播源的精度可以提高到兩倍多。

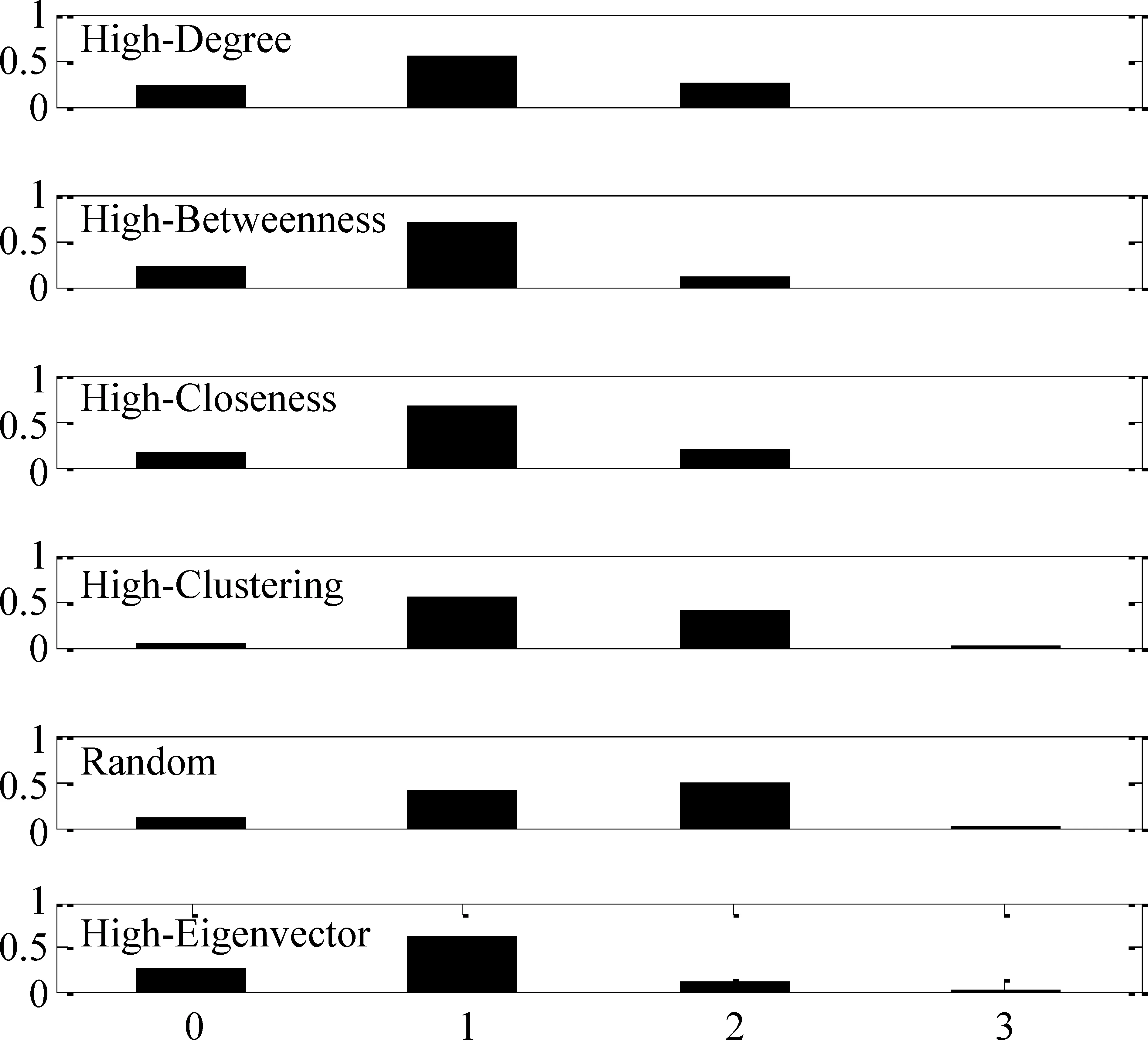
圖4 無標度網絡在各種觀察點部署策略下溯源算法的錯誤距離分布

圖5是倉鼠網絡在各種觀察點部署策略下溯源算法的錯誤距離分布圖。在觀察點部署策略隨機、度、聚類系數、介數、緊密度以及特征向量下估計傳播源的精度分別為0.06、0.00、0.11、0.00、0.14以及0.16。實驗結果表明，采用特征向量觀察點部署策略估計傳播源的精度高于其他策略；另外，相比隨機選擇策略，采用特征向量觀察點部署策略，準確定位傳播源的精度可以提高到兩倍多。

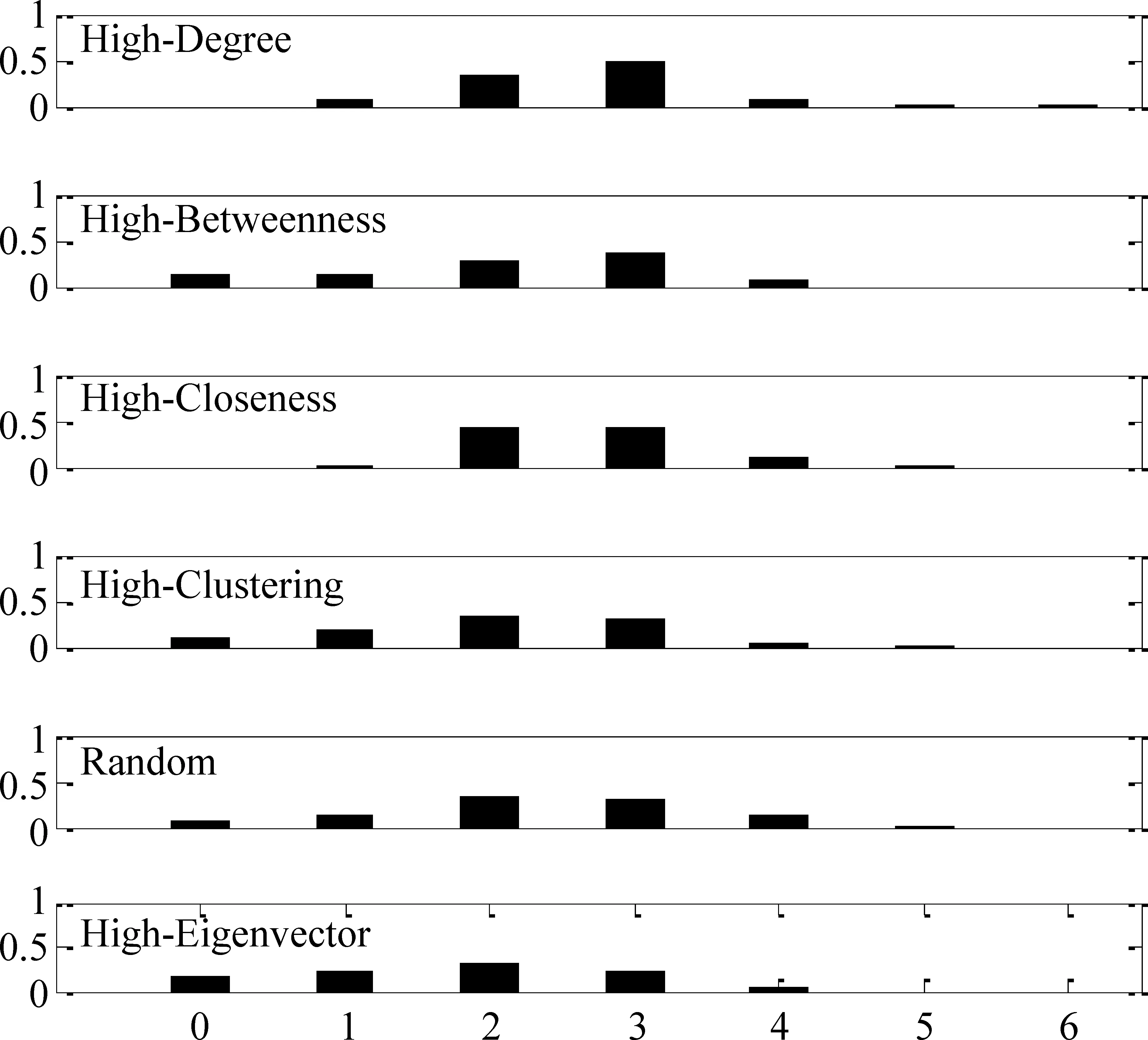
圖5 倉鼠網絡在各種觀察點部署策略下溯源算法的錯誤距離分布

圖6是美國電力網絡在各種觀察點部署策略下溯源算法的錯誤距離分布圖。需要說明的是，在文獻[10] 中指出在真實美國電力網絡上采用基于傳播中心性溯源算法的精度只有3%，在實驗中利用這六種觀察點部署策略估計真實傳播源的精度最高的也只有1%。因為精度極低再加上錯誤距離最大的已經達到20跳，而美國電力網絡的精度用的是錯誤距離在3跳以內的比例。在觀察點部署策略隨機、度、聚類系數、介數、緊密度以及特征向量下估計傳播源的精度分別為0.23、0.12、0.24、0.21、0.25以及0.27。實驗結果表明，采用特征向量觀察點部署策略估計傳播源的精度高于其他策略；另外，相比隨機選擇策略，采用特征向量觀察點部署策略，準確定位傳播源的精度可以提高到兩倍多。

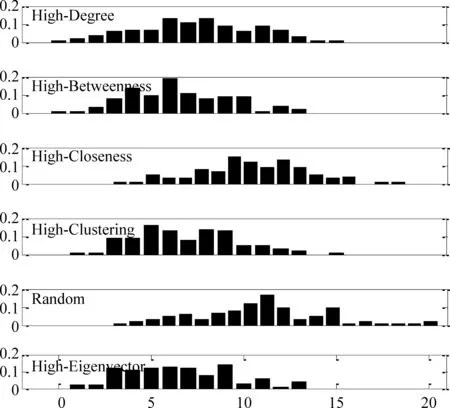
圖6 美國電力網絡在各種觀察點部署策略下溯源算法的錯誤距離分布

圖7是合著關系網絡在各種觀察點部署策略下溯源算法的錯誤距離分布圖。在觀察點部署策略隨機、度、聚類系數、介數、緊密度以及特征向量下估計傳播源的精度分別為0.02、0.02、0.01、0.00、0.02以及0.05。實驗結果表明，采用特征向量觀察點部署策略估計傳播源的精度高于其他策略；另外，相比隨機選擇策略，采用特征向量觀察點部署策略，準確定位傳播源的精度可以提高到兩倍多。

圖7 合著關系網絡在各種觀察點部署策略下溯源算法的錯誤距離分布

圖8是線蟲代謝網絡在各種觀察點部署策略下溯源算法的錯誤距離分布圖。在觀察點部署策略隨機、度、聚類系數、介數、緊密度以及特征向量下估計傳播源的精度分別為0.06、0.01、0.05、0.00、0.00以及0.08。實驗結果表明，采用特征向量觀察點部署策略估計傳播源的精度高于其他策略。

圖8 線蟲代謝網絡在各種觀察點部署策略下溯源算法的錯誤距離分布

本實驗在上述七種網絡拓撲結構上測試了這六種觀察點部署策略對采用反向貪心溯源算法定位傳播源精度的影響，將測試結果整理在表2中，并在表中將最優的性能值加粗表示。從表2可看出，采用特征向量觀察點部署策略更有利于提高估計傳播源的精度。另外，在無標度網絡、隨機網絡、美國電力網絡、倉鼠網絡以及合著關系網絡這些網絡上。相比隨機選擇策略，采用特征向量部署策略，準確定位傳播源的精度可以提高到兩倍多。從這些錯誤距離分布圖中可以看出每個網絡都隨著觀察點部署策略的改變而改變，但是在各個網絡中錯誤距離分布的趨勢很相似。

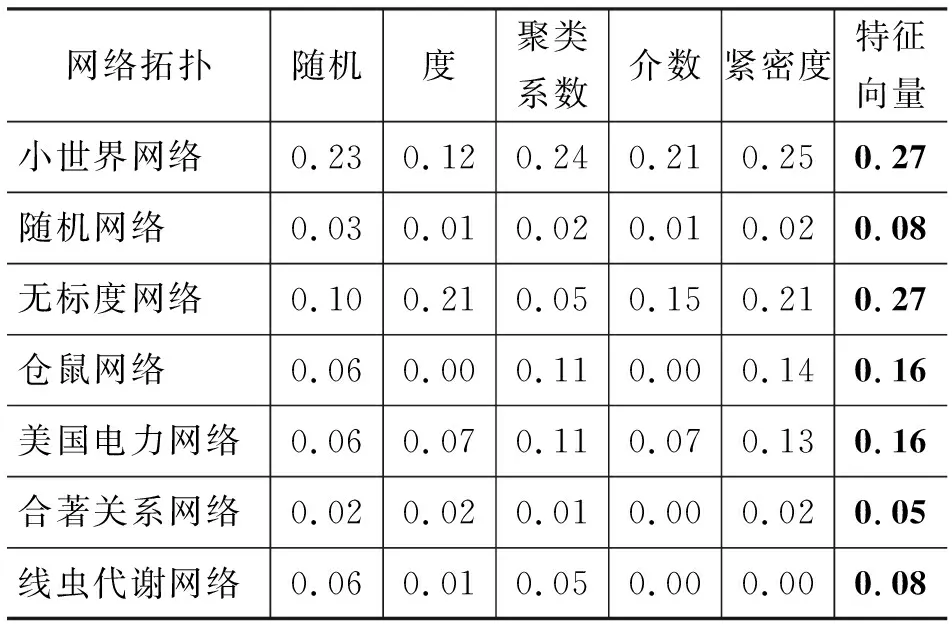
表2 各種網絡在六種觀察點部署策略下定位傳播源的精度

5 總結

在網絡中估計傳播源是一項重要的研究課題。估計傳播源的一種可行的方法，即是利用觀察點收集的部分節點信息來定位傳播源。故而，估計傳播源與觀察點的部署策略緊密相關。本研究評估了幾種觀察點部署策略，含度數、介數、緊密度、聚類系數、特征向量和隨機。利用SI傳播模型和反貪心溯源算法，在合成網絡和真實網絡上仿真模擬。實驗結果表明，采用特征向量觀察點部署策略更有利于提高估計傳播源的精度，且與隨機選擇觀察點部署策略相比，在某些網絡上估計的傳播源精度可以提高到兩倍多。

基于節點中心性的觀察點部署策略與采用的估計傳播源的算法相關，而這些觀察點部署策略對于其他溯源算法精度的影響需要進一步研究。是否能找到一種策略可以適用各種溯源算法，這些問題將會在以后的工作中做進一步的討論。