不等精度數據融合的最優權值與參數估計方法

張志敏

(中國人民解放軍92941部隊44分隊，遼寧葫蘆島 125001)

0 引言

不同類型和不等精度數據的融合是測量數據融合處理中的常見難題，也是研究的熱點問題［13］。測量數據融合處理的主要目的就是提高參數估計的精度，建立合適的數學處理模型，給出高效可靠的融合算法，建立既能夠適合數學處理，又能夠體現物理過程、工程特征的融合處理模型是關鍵。模型包括測量數據的模型和目標軌跡模型，而測量數據建模又包括測量誤差建模與測量目標真實信號建模。不同類型和不等精度數據是指觀測數據中關于待估參數的函數關系不同、各階導數也不同［45］。因此，針對不同類型不等精度的觀測數據的融合處理，使用不同的加權方法，會對參數估計結果造成較大的影響。因此針對不同的應用背景研究適合的加權融合處理方法成為提高不同類型和不等精度數據的融合參數估計精度的關鍵。

對于線性回歸模型，已有文獻 ［6］證明了其參數估計，以及不等精度測量數據的唯一最優加權原則 。但是對于非線性回歸模型，當前的研究結果都是利用線性回歸模型的處理思維以及迭代算法，求解非線性回歸問題，在基于觀測數據的隨機誤差是獨立同分布等精度條件下推導的［7-9］，不進行加權處理，或直接采用線性模型的高斯－馬爾科夫定理對不同類型的觀測數據進行加權處理，對于參數估計的精度的提高存在很大的局限性。非線性回歸模型的非線性程度會對參數估計的偏差、方差等因素產生影響，因此通過什么方法可以降低模型的非線性程度，成為長久以來非線性模型研究領域的難點。文獻［10］通過引入非線性模型的參數效應曲率和固有曲率，使降低曲率相當于降低模型非線性程度，采用曲率表征模型的非線性程度，目前該理論已成為非線性模型定量分析的理論基礎，為非線性回歸模型的研究提供一種新的思路，極大地促進了不同類型不等精度測量數據非線性融合的權值問題的研究。

對于不同種類的不等精度測量數據融合處理的權值與參數估計的問題，根據對參數估計偏差和均方誤差進行分析的結論，從理論上證明了對于非線性模型在不同類型不等精度數據融合處理時，最優融合權值不僅與數據本身精［6］度有關，而且與模型的結構、導數相關聯，且線性模型高斯－馬爾科夫定理不再適用。給出了多結構多元非線性融合模型的最優權值與參數估計的計算方法，最后通過四個算例的對比驗證，可以證明該方法是有效可靠的。

1 不等精度觀測數據線性融合的最優權值和參數估計

針對參數βp×1的估計問題，假如有兩類線性測量數據，其觀測方程如下所示:

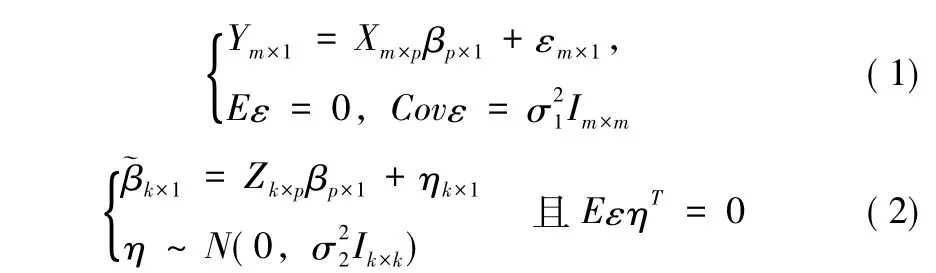
對于兩類不等精度線性觀測數據融合模型 (1)－(2)的參數估計，構造如下模型所示:

定理 1: 記 λi，1，λi，2，i=1，…，p分別為矩陣 XTX，ZTZ的特征值，那么融合模型的最優權值和參數估計形式如下所示:

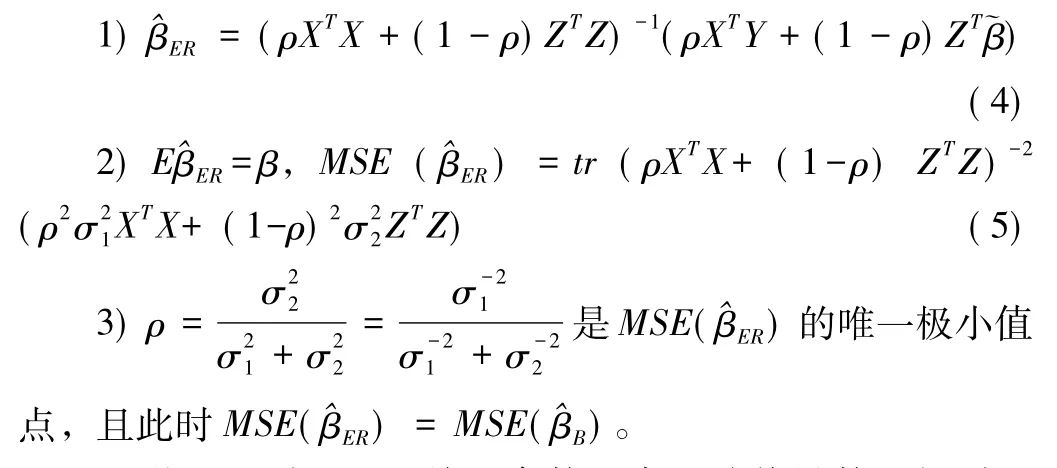
證明:1)由 (3)關于參數β求一階偏導數，得到正規方程為:

因此，得到1)。

2)將 (4)式代入，并由模型 (1)、(2)的假設，計算即可得到 (5)的第一式。

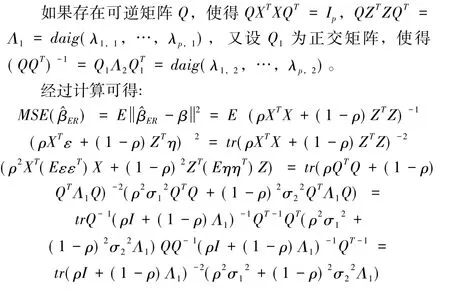
即定理1的結論3)成立。

定理1的結論3)具有重要的應用價值。在處理實際問題時，(1)、(2)一般為不等精度的測量數據，在這些數據的融合處理時，數據的加權對于數據處理精度具有重要影響。結論3)說明不等精度的線性觀測數據融合處理時唯一最優融合權值由測量數據的精度決定，這本質上仍然是線性模型最小二乘估計的Gauss－Markov定理。

2 不等精度觀測數據非線性融合的加權和參數估計

在很多估計問題中，往往要考慮異類不等精度非線性觀測數據的融合處理［2］。這里，我們提出的異類數據，具體指觀測數據關于待估參數的函數關系不同，因而它們的模型結構也不一樣，參數估計的精度對其依賴程度自然也是不同的。則不同結構的觀測數據的權值也應該是不同的。

2.1 非線性模型參數估計的方差和偏差

當測量數據是待估參數的非線性函數，由于非線性問題往往只有迭代解 (沒有解析解)，估計的性質與線性模型有本質的不一樣。

考慮如下一元非線性模型 (18)的參數估計的偏差和方差:

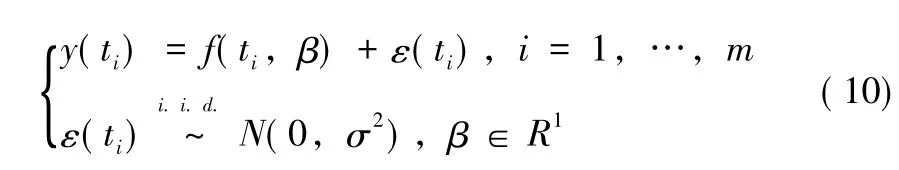
對于模型 (10)，為了得到其估計的性質，假設:(i)f(t，β)關于參數β存在一階連續導數，且:

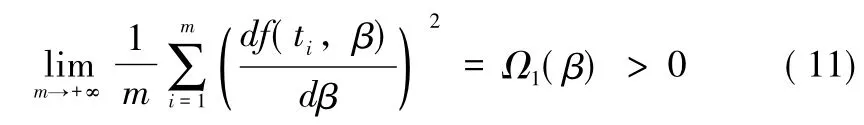
(ii)f(t，β)關于參數β存在二階連續導數，且:

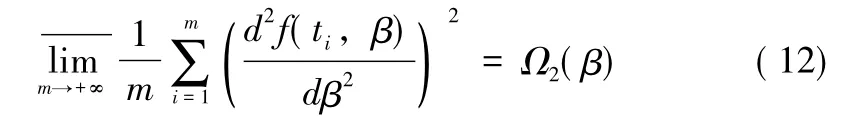
條件 (i)、(ii)自然而又必要的，因為在假設 (10)下，觀測向量關于參數的 Fisher信息陣為因此，就表示觀測中平均每個樣本所包含的有關參數的Fisher信息。對于模型 (10)，我們有如下結論:

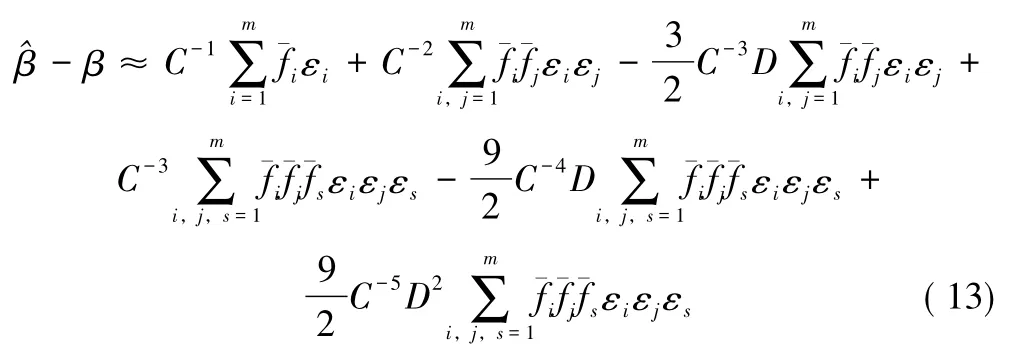
則參數估計的偏差和均方誤差就有如下所示近似:

由定理2可知，非線性模型的參數估計是有偏的，其偏差和方差的值不但與測量數據的精度有關，而且同模型的一、二階導數 (即模型的結構)有關，則與模型曲率也有關系［2-3］。模型曲率可等價于函數的非線性程度，故降低模型曲率可以降低函數非線性程度，從而有效地改善非線性模型的參數估計效果。

2.2 一元非線性融合模型的最優權值和參數估計

為了方便討論，我們先只探究非線性回歸模型:

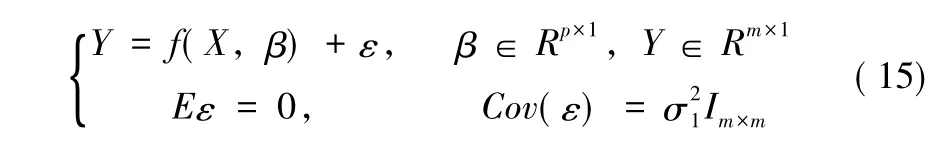
在線性約束模型 (2)(事實上，模型 (2)不僅可以當作先驗信息，也可以當作另一類系統的測量數據)下的參數估計。根本上，兩類系統的測量數據融合的最優權值問題，在參數估計均方誤差最小的準則下，歸結為尋找ρ，使得極小值問題:

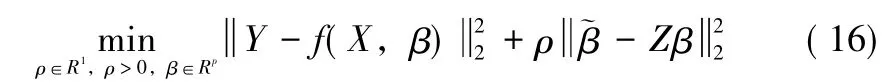
的解滿足MSE(β^)(ρ)=E||(β^)(ρ)－ β||2=min［25］。

對于一元非線性模型，定理3提出了參數估計的偏差與均方誤差，定理4提出了最優權值的存在性及其性質。

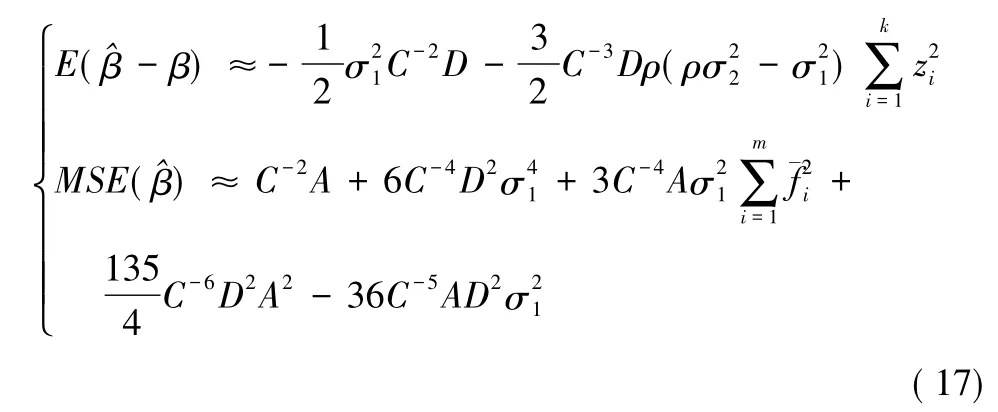
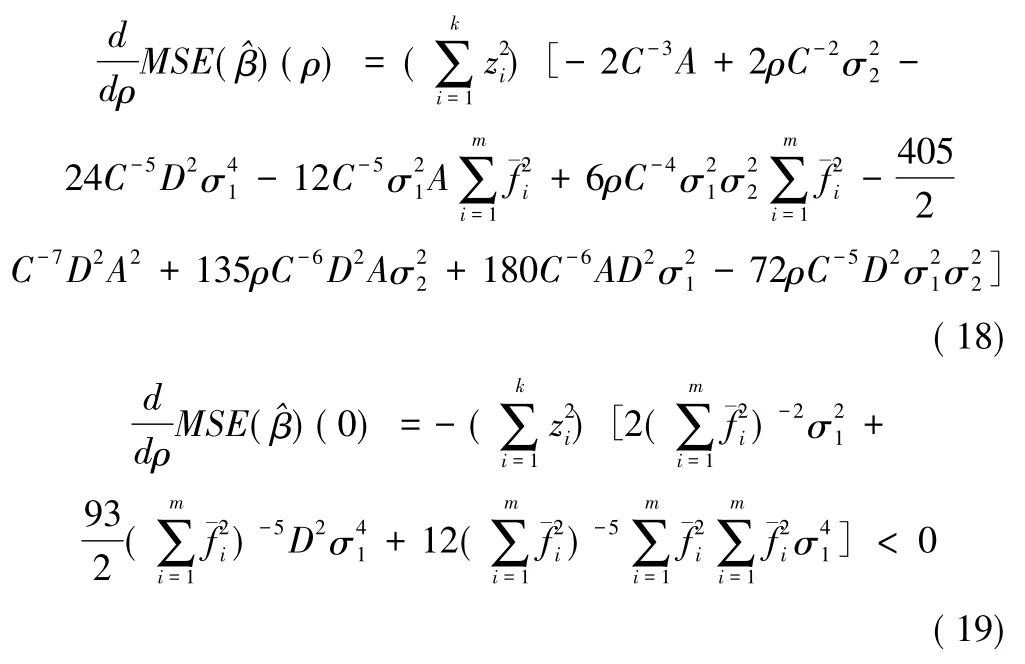
當ρ→+∞時，由第三項起始，之后的每項都是前兩項的高階無窮小量，又當時，前面兩項之的和大于零，故存在ρ0＞0，使當＞0，因而

因此對于極小值問題 (16)的求解，我們按如下的迭代方式，確定多結構不同類型非線性測量數據融合的最優權值及相應的參數估計，算法步驟如下:

步驟2:由 (17)中的第二式，計算參數估計的均方誤差在處的值

步驟4:將ρ1賦值給ρ0，重復步驟1，根據給定的收斂準則，重復上述四個步驟，一直迭代至收斂，此時的ρ1為最優融合權值，為參數的最優估計。

2.3 多結構多元非線性融合模型的最優權值與參數估計

根據如下所示的多結構多元非線性融合模型:

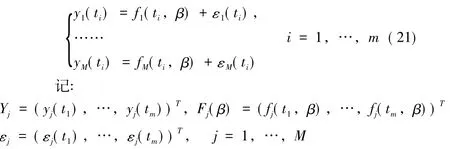
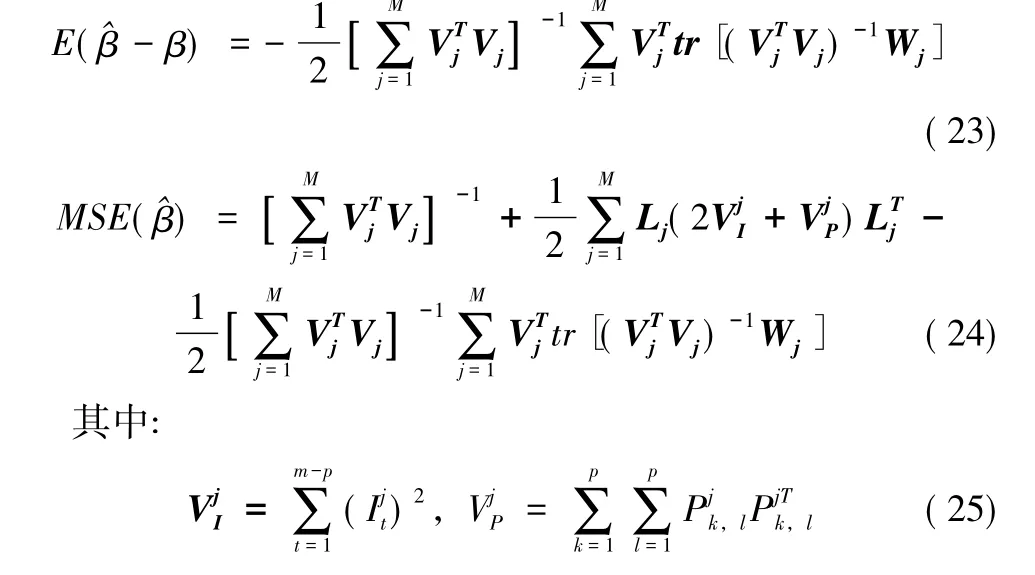
Vj=是上三角矩陣，的列向量是標準正交基。

定理5的證明過程類似于定理3和定理4，但此時由于參數是多維的，涉及到多元非線性函數的模型曲率求解，具體證明方法可參考文獻［6］。

步驟1:對于給定的一組權值 ρ(0)，設定迭代初值β(0)，使用觀測數據關于待估參數的函數式獲得到Fj(β(0));

步驟2:記ei為第i個分量為1，其他分量全為0的向量，根據設定數值微分的步長h(根據實際情況，一般可設定為h=10－6)，計算Fj(β(0))梯度矩陣:

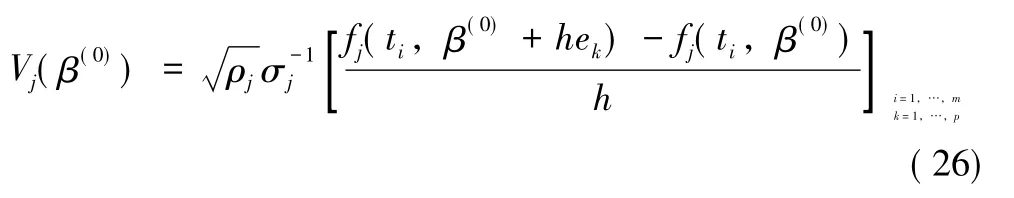
并對此進行QR分解，得到矩陣Lj(β(0));

步驟3:由下式得到參數β的一次改進:

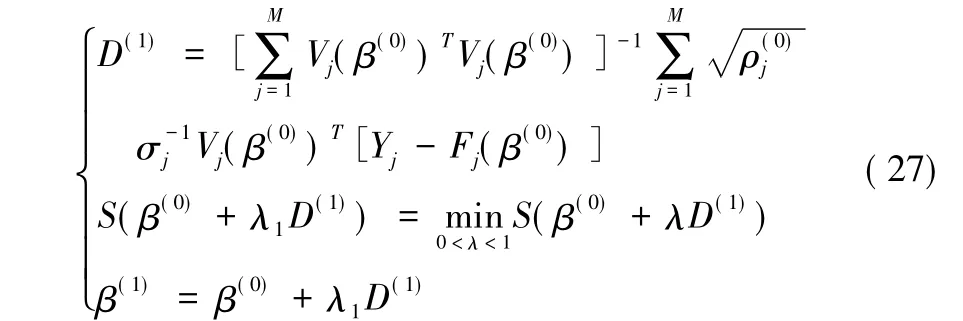
步驟4:對于給定的收斂閾值τ＞0，如果|S(β(1))－S(β(0))|＜τ，則迭代結束，令轉入Step5;否則，令β(0)=β(1)，返回Step1;

3 算例驗證

算例1:設某物理量u真值為10，有不等精度的兩套設備對其進行直接測量，分別得到100個高精度的觀測數據 (均方根差為1)，180個低精度的觀測數據 (均方根差為4)，共產生100組觀測數據，得到的參數u的估計及方差見表1。(估計的根方差是對100組觀測數據統計得到。)

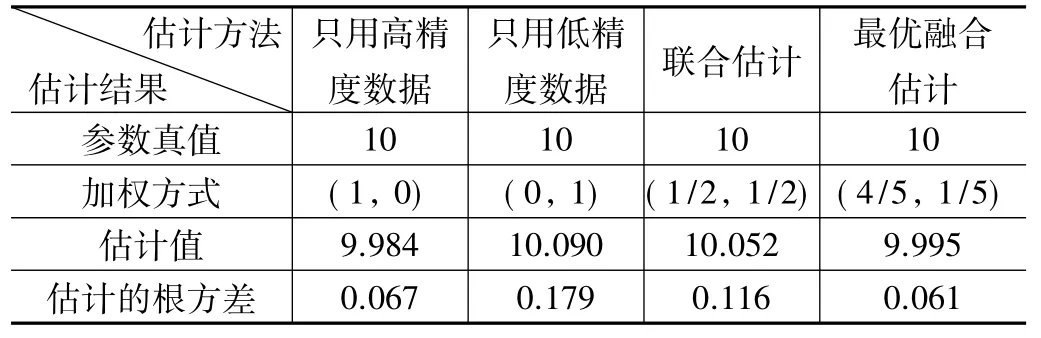
表1 四種估計的比較

在線性觀測數據融合處理時，唯一的最優融合權值由測量數據的精度決定;求解極小值問題 (8)100次，得到均方誤差為0.061，估計是最優的。

算例2(一元非線性融合模型的最優權值與參數估計):

設 f(tj，β) = 1+(5+tjβ)0．1，y(tj) = f(tj，β)+ε(tj)，ε(tj)i～idN(0，0．052)，z(si)=β+η(si)，η(si)i．～i．dN(0，0.012)，令tj=0．05 × (j－ 1)，j=1，…，300，si=2+0．1×(i－1)，i=1，…，100，β的真值為8，產生50組觀測數據計算結果見表2，均方誤差與加權因子關系見圖1。

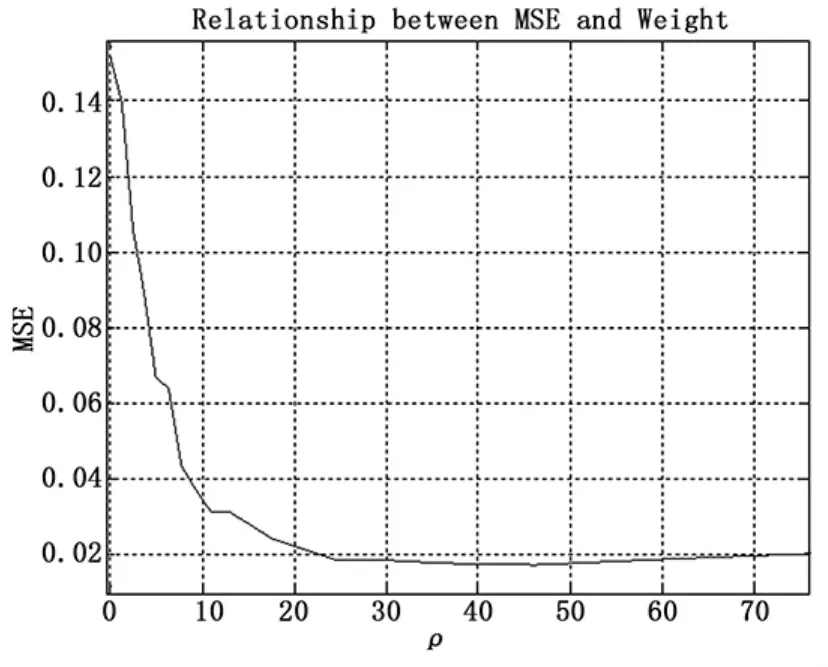
圖1 均方誤差和加權因子關系圖

當采用線性模型的加權方式，即取權值ρ=0.052/0.012時，得到均方誤差為0.020;而當ρ=1．80×0.052/0．012時，參數估計的均方誤差得到最小，其值為0.017。

表2 各種加權的參數估計結果對比

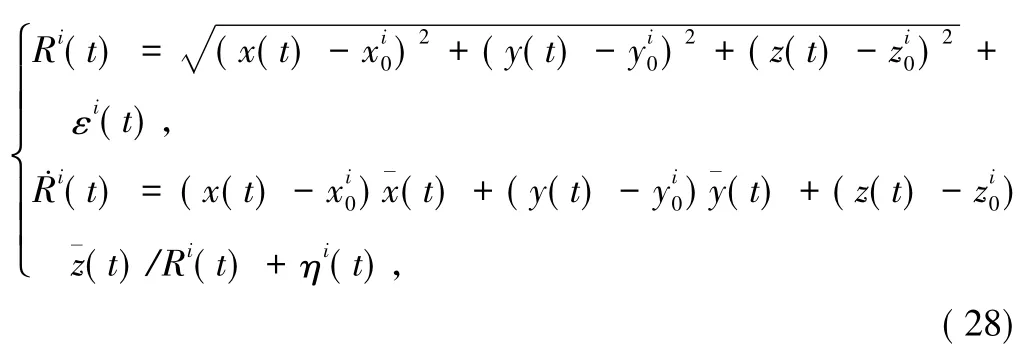
算例3(彈道目標跟蹤)。

以連續波雷達和自主外測設備構建多測距測速彈道目標跟蹤系統，假設有3個測量站，分別測量彈道目標的距離R和速度R，測量值可以表達為:

假設各觀測量測量誤差服從高斯分布，且各觀測站的觀測量互不相關，滿足獨立同分布條件:

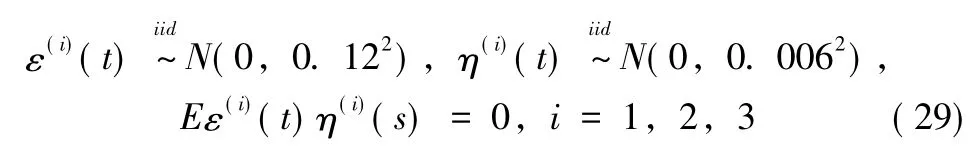
仿真參數設置如下:各觀測量的采樣率為20 Hz，即t=0．05×j，j=1，…，600， 各測量站的站址坐標為，i=1，2，3，彈道目標在t時刻的狀態矢量可表示為利用理論彈道帶入公式(28)生成由彈道目標的距離R和速度組成的觀測數據本例采用文獻 ［4］提出的節省參數建模方法，利用不等間距最優節點的三次樣條函數對彈道進行建模，采用最小二乘法對該非線性回歸模型的樣條系數和彈道參數進行估計，ρ為最優權值，仿真次數為100次。

仿真結果表明:當ρ=0．122/0．0062時，MSER(ρ)=0.322 m，MSEV(ρ)=0.049 3 m/s; 當 ρ = 2．33 ×0.122/0.0062時，MSER(ρ)，MSEV(ρ)達到最小值，其值分別為0.082 m，0.029 4 m/s。可以看出，多結構多元非線性融合模型可以有效提高彈道目標的估計精度。

算例4(多測速聯合定軌)

依靠同一時刻的N個(N≥6)以上的測速元，可以確定該時刻的軌道參數 X(t)。以(xk，yk，zk)，(k=1，2，．．，N)為N個互不相同的測站在相同坐標系下的站址坐標，N個測速可表示為:

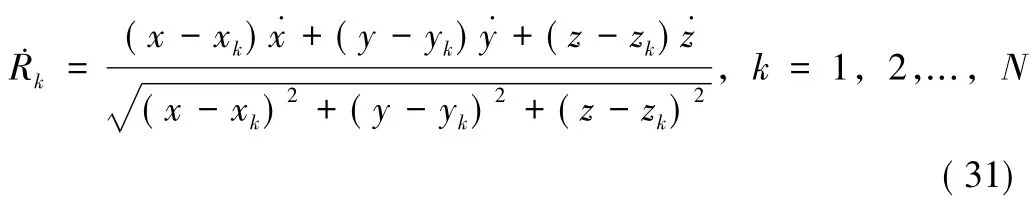
上式就是聯系測速元與目標位置和目標速度的測量方程。對于是 N個互不相同的站址，Jacobi(雅克比)矩陣為:

表3 測速定軌結果與基準軌道作差統計表

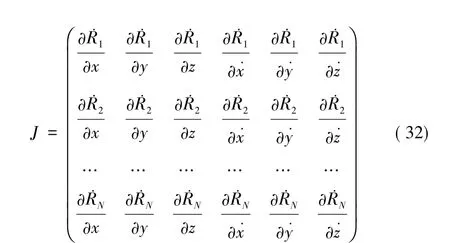
若雅克比矩陣是列滿秩矩陣，從而由反函數存在定理，可以有由式(1)唯一地確定軌道參數:

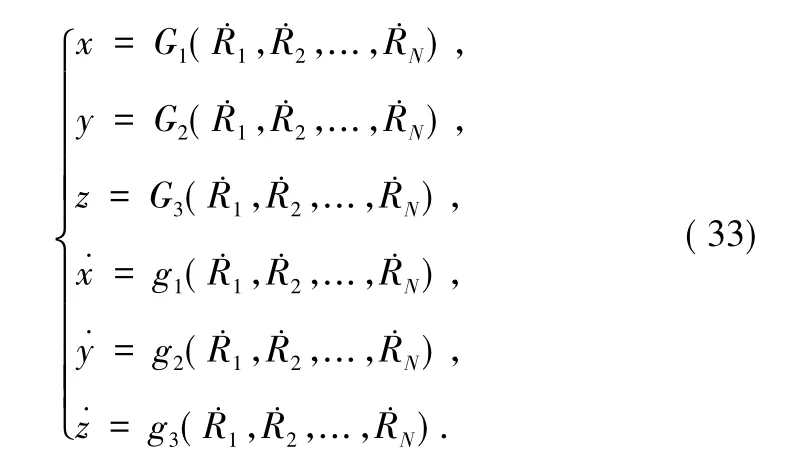
假設各觀測量測量誤差服從高斯分布，且各觀測站的觀測量互不相關，滿足獨立同分布條件:

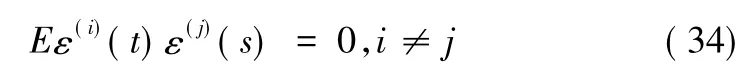
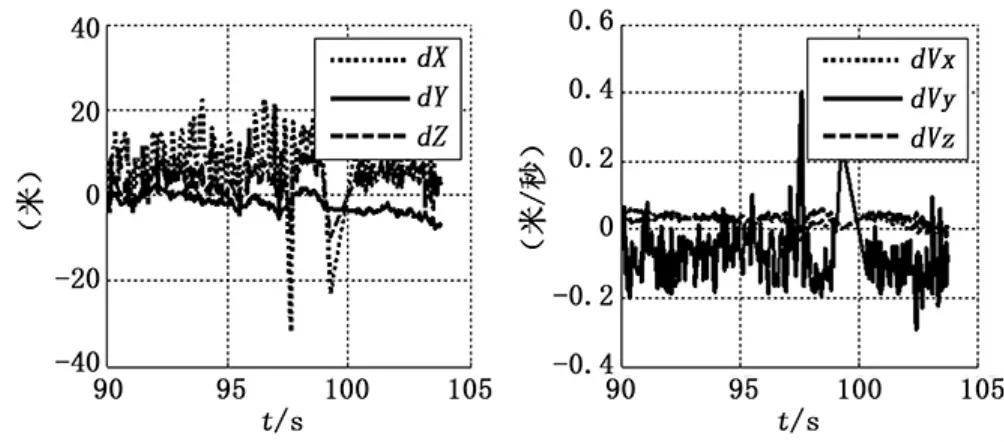
圖2 平均加權定軌結果與基準彈道減法統計圖(0.1 m/s的隨機誤差，左圖為位置，右圖為速度)

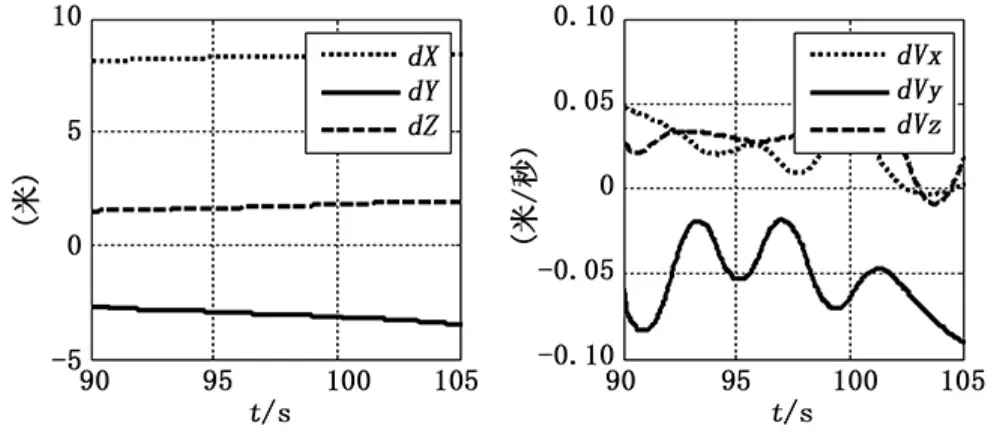
圖3 最優加權定軌結果與基準軌道減法統計圖(0.1 m/s的隨機誤差，左圖為位置，右圖為速度)

圖2和圖3分別為加0.1 m/s的隨機誤差條件下平均加權和最優加權定軌結果與基準彈道作差統計結果，由圖可知平均加權方式的差值波動較大，而最優加權方式的波動較小。此外，從表中3均值和標準差的統計結論可以看出，采用非線性回歸模型最優融合估計方式進行多測速定軌可以不同測速元測量精度差異對定軌精度的影響，精度高于平均估計加權方式，滿足靶場試驗高精度測量系統定軌應用需求。

4 結論

測量數據的融合處理是提高數據處理精度的有效措施。本文研究了不等精度觀測數據融合的權值和參數估計問題。對于線性融合模型，其最優權值由測量數據的精度唯一確定，這與經典的Gauss－Markov定理是一致的;而對于非線性融合模型，通過參數估計的均方誤差的曲率矩陣表達，建立了多結構不等精度非線性回歸模型的最優加權理論與算法，并給出了計算實例，結果表明:多結構非線性回歸模型的加權數值會對參數估計精度產生非常大的影響，其最優權值不僅僅和其他各類數據的測量誤差統計特性相關聯，還與各類數據模型的結構，即模型曲率、樣本量的大小等有關，從而由線性模型Gauss－Markov定理得到權值(僅與觀測數據精度有關)不再是最優的。