兩階段RDD方法無回答的影響及其改進(jìn)
李 鋒
(首都經(jīng)濟(jì)貿(mào)易大學(xué) 統(tǒng)計(jì)學(xué)院,北京 100070)
0 引言
調(diào)查的最終目的是獲取真實(shí)的數(shù)據(jù)。為了掌握社會(huì)經(jīng)濟(jì)方面的信息,政府及其他部門組織的以居民及住戶為調(diào)查對(duì)象的調(diào)查日漸增多,比如消費(fèi)者信心指數(shù)調(diào)查等,但是一直沒有建立起完整的居民及住戶抽樣框。常用的住戶抽樣框主要有兩種,一種是以戶籍為標(biāo)準(zhǔn)的戶口抽樣框,戶口抽樣框在人戶分離問題嚴(yán)重的背景下失去現(xiàn)實(shí)基礎(chǔ),抽樣框誤差較為嚴(yán)重;另一種是以住宅為標(biāo)準(zhǔn)的抽樣框,具體又可以采用入戶派員面訪、(固定)電話調(diào)查和郵寄調(diào)查,此外,還有以手機(jī)、郵箱等為抽樣框的居民調(diào)查框。
1 Mitofsky-Waksberg兩階段RDD方法
1.1 計(jì)算機(jī)輔助調(diào)查的一般抽樣設(shè)計(jì):計(jì)算機(jī)隨機(jī)撥號(hào)
電話訪問與入戶訪問是僅有的兩種可以實(shí)施住戶隨機(jī)抽樣的方法。隨著電話普及率不斷增高,而且也迫于大都市入戶訪問成功率越來越低的現(xiàn)狀,面訪已經(jīng)被計(jì)算機(jī)輔助電話調(diào)查CATI(Computer Assisted Telephone Interviewing System)所取代,傳統(tǒng)的固定電話簿技術(shù)已經(jīng)被計(jì)算機(jī)隨機(jī)撥號(hào)RDD(random digit dialing)技術(shù)所取代。將區(qū)號(hào)和電話號(hào)碼的前四位(八位號(hào)碼)或者前三位(七位號(hào)碼)的組合號(hào)段作為初級(jí)單元,將電話號(hào)碼的后四位作為次級(jí)單元,每個(gè)初級(jí)單元包含的次級(jí)單元均相等為10000。傳統(tǒng)的計(jì)算機(jī)隨機(jī)撥號(hào)設(shè)計(jì)分兩步:首先隨機(jī)抽取一定數(shù)量的初級(jí)單元,在抽中的號(hào)段中再隨機(jī)抽取后四位號(hào)碼得到完整的電話號(hào)碼,最終,在每個(gè)抽中的號(hào)段中抽取一定數(shù)量的住戶為樣本。這種撥號(hào)方法實(shí)際上是每階段抽樣都是簡(jiǎn)單隨機(jī)抽樣的二階抽樣,估計(jì)量及方差的計(jì)算都有現(xiàn)成的公式,但是這種方法有兩個(gè)問題,一是樣本中的住戶太少,有很多空號(hào)和單位電話;二是無回答在各個(gè)號(hào)段并不是等比例分布,因此,抽樣過程較為復(fù)雜,估計(jì)還可能有偏。
1.2 隨機(jī)撥號(hào)的改進(jìn)
Mitofsky和Waksberg提出了一種方法對(duì)計(jì)算機(jī)隨機(jī)撥號(hào)進(jìn)行改進(jìn),稱為Mitofsky-Waksberg兩階段抽樣法,設(shè)計(jì)分兩步:第一步首先隨機(jī)抽取初級(jí)單元,在抽中的號(hào)段中再隨機(jī)抽取一個(gè)后四位號(hào)碼得到一個(gè)(或多個(gè))電話號(hào)碼,如果這個(gè)號(hào)碼是住宅號(hào)碼,則定為一類初級(jí)單元PSU,如果這個(gè)號(hào)碼不是住宅號(hào)碼,則放棄這個(gè)初級(jí)單元(號(hào)段)。第二步在每個(gè)一類初級(jí)單元(號(hào)段)中,再抽取k-1個(gè)號(hào)碼。最終,在每個(gè)一類號(hào)段中抽取相同數(shù)量的住戶為樣本。這種撥號(hào)方法實(shí)際上是第一階為PPS抽樣(與初級(jí)單元規(guī)模成比例的不等概率抽樣),第二階為抽取等量單元的簡(jiǎn)單隨機(jī)抽樣的二階抽樣設(shè)計(jì),設(shè)總體初級(jí)單元(號(hào)段)有N個(gè),第i個(gè)單元中住戶數(shù)為Mi,總的住戶數(shù)為M0,從N個(gè)單元中抽取n個(gè)單元進(jìn)行調(diào)查,在每個(gè)抽中的初級(jí)單元共抽取m個(gè)單元,則總體中第j基本單元(住戶)入樣概率均為P(ij)=P(j|i)P(i)=(m/Mi)(Mi/M0)=m/M0。
因此,Mitofsky-Waksberg兩階段RDD方法理論上估計(jì)量及方差都是自加權(quán)的,有現(xiàn)成的公式,也可以根據(jù)一家多部電話等進(jìn)行調(diào)整。這種方法可以大大提高抽樣單元中的住戶的數(shù)量。
2 計(jì)算機(jī)輔助調(diào)查實(shí)施中存在的無回答率問題
2.1 無回答率較高,且不同初級(jí)抽樣單元內(nèi)無回答率不同,不處理偏倚較大
調(diào)查過程中,合格受訪者因各種因素?zé)o法接受訪問,即為無回答,對(duì)于任何一種訪問方式,當(dāng)其目標(biāo)被訪者的無回答率超過40%①以上時(shí),其隨機(jī)樣本的代表性就存在問題。而由于電話詐騙較為猖獗,當(dāng)前我國(guó)計(jì)算機(jī)隨機(jī)撥號(hào)訪問的無回答率常常能達(dá)到80%左右。直接應(yīng)用全部樣本數(shù)據(jù),對(duì)無回答不作任何處理,當(dāng)成自加權(quán)樣本實(shí)施推斷,估計(jì)量只能代表回答者的情況,估計(jì)量很可能出現(xiàn)較大偏倚。
令Yij為總體第i個(gè)初級(jí)單元中的第j個(gè)次級(jí)單元的指標(biāo)值,i=1,2,…,N;j=1,2,…,Mi。yij為樣本中第i個(gè)初級(jí)單元中第 j個(gè)次級(jí)單元的指標(biāo)值,i=1,2,…,n;j=1,2,…,mi。是總體(樣本)初級(jí)單元的指標(biāo)和,是總體(樣本)第i個(gè)初級(jí)單元指標(biāo)按次級(jí)單元的平均數(shù)總體(樣本)按次級(jí)單元的平均數(shù);在上述自加權(quán)的設(shè)計(jì)下,假定所有抽中的單元均回答,第i個(gè)初級(jí)單元內(nèi)調(diào)查單元mi等于回答單元m,則總體總量的估計(jì)量:

如果考慮無回答率,假設(shè)第i個(gè)初級(jí)單元中回答率為r1i,無回答率為r0i,則被調(diào)查單元回答單元的均值為回答單元的均值為總體總量的估計(jì)量:

如果仍然按自加權(quán)設(shè)計(jì)估計(jì),偏差為:

可見,估計(jì)的偏倚既受到初級(jí)單元的回答率影響,也受到回答者與回答者之間的差異影響,同時(shí)差異的結(jié)構(gòu)也影響偏倚的大小。本文簡(jiǎn)單地忽略回答者和無回答者的差異,同時(shí)也忽略了初級(jí)單元回答率的高低和差異。
2.2 采用初級(jí)單元內(nèi)加權(quán)方法處理總的估計(jì)量不再是自加權(quán)的,方差估計(jì)很困難
如果有大量的無回答,就需要調(diào)整無回答,常規(guī)的處理方法是對(duì)每個(gè)初級(jí)單元內(nèi)的無回答群體實(shí)施調(diào)查,然后加權(quán)得到每個(gè)初級(jí)單元內(nèi)的估計(jì)量,即用二重抽樣法進(jìn)行估計(jì)。由于無回答在各個(gè)號(hào)段之間并不是等比例分布,加權(quán)之后各個(gè)號(hào)段(初級(jí)單元)中的調(diào)查單元不是相同的,這樣Mitofsky-Waksberg兩階段RDD方法得到的估計(jì)量實(shí)際上不再是自加權(quán)的。由于第一階抽樣是PPS抽樣,第二階是二重分層抽樣,抽樣過程較為復(fù)雜,方差估計(jì)需要在每一個(gè)初級(jí)單元內(nèi)部根據(jù)二重分層抽樣的方法計(jì)算方差,再計(jì)算二階抽樣的方差估計(jì),十分復(fù)雜。
3 無回答誤差的抽樣設(shè)計(jì)改進(jìn)
3.1 隨機(jī)組法
隨機(jī)組法就是從總體中抽取k個(gè)(k≥2)的樣本(通常每個(gè)樣本是一樣的抽樣設(shè)計(jì)),對(duì)每一個(gè)樣本分別構(gòu)造所感興趣的總體參數(shù)θ(如總體均值)的一個(gè)估計(jì)量,α=1,2,…,k。如果這些估計(jì)量互不相關(guān)而且有共同的數(shù)學(xué)期望μ,這樣總體參數(shù)θ的全樣本估計(jì)量θ定義為:

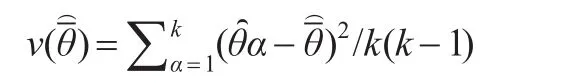
如果數(shù)學(xué)期望μ=總體參數(shù)θ,則估計(jì)量是無偏估計(jì)。
3.2 基于隨機(jī)組法的抽樣設(shè)計(jì)
實(shí)際操作中,通常是將全部樣本劃分成R組,每一組都遵循同樣的設(shè)計(jì),這種偽隨機(jī)在總體單元遠(yuǎn)大于樣本量時(shí),可以視為獨(dú)立復(fù)制。如果直接在初級(jí)單元內(nèi)設(shè)計(jì)隨機(jī)組,容易破壞群結(jié)構(gòu),為了不破壞群結(jié)構(gòu),并且能夠通過盡量多地保留原始數(shù)據(jù)的信息,本文建議采取分層抽樣的方式隨機(jī)撥號(hào)基礎(chǔ)上的隨機(jī)組法。具體方式如下:
一是將全部號(hào)段分層,如將號(hào)段分為直轄市城市住戶、直轄市農(nóng)村住戶、東部住戶、中部住戶、西部住戶等。
二是在每層內(nèi)實(shí)施Mitofsky-Waksberg兩階段抽樣法,在每個(gè)層內(nèi)抽取k個(gè)一類初級(jí)單元PSU(號(hào)段),在每個(gè)號(hào)段內(nèi)抽取到同等數(shù)量的回答者。
三是對(duì)每個(gè)號(hào)段內(nèi)的無回答者實(shí)施簡(jiǎn)單隨機(jī)抽樣,在每個(gè)號(hào)段內(nèi)抽取到同等數(shù)量的無回答者。
四是在各個(gè)層內(nèi)采取隨機(jī)組號(hào)分配的方式,構(gòu)造k個(gè)隨機(jī)組。在第一層中,第一個(gè)號(hào)段分派一個(gè)1到k之間的隨機(jī)數(shù),例如分派數(shù)為k-1,就分到第k-1個(gè)隨機(jī)組,則第二個(gè)號(hào)段分配數(shù)為k,第三個(gè)號(hào)段分配數(shù)為1,以此類推。
五是用隨機(jī)組法得到整體的估計(jì)量及方差,也可以得到每一層的估計(jì)量。
通過這種方法能夠構(gòu)造出抽樣設(shè)計(jì)完全相同的k個(gè)隨機(jī)組,得到的總體參數(shù)(均值、總量等)的估計(jì)量以及估計(jì)量方差的無偏估計(jì)量。
兩階段RDD方法電話調(diào)查模擬數(shù)據(jù)隨機(jī)組構(gòu)造如表1所示。

表1 兩階段RDD方法電話調(diào)查模擬數(shù)據(jù)隨機(jī)組構(gòu)造
4 結(jié)束語
計(jì)算機(jī)輔助電話調(diào)查已經(jīng)成為我國(guó)對(duì)住戶實(shí)施抽樣調(diào)查的主要方式,Mitofsky-Waksberg兩階段抽樣法雖然提高了撥到住戶的比例,但在無回答廣泛存在的情形下,估計(jì)量不再是自加權(quán)的,而且可能有偏。本文認(rèn)為應(yīng)該對(duì)無回答者實(shí)施抽樣,加權(quán)得到每一個(gè)初級(jí)單元的估計(jì)量,通過結(jié)合分層技術(shù),可以得到隨機(jī)組下的無偏估計(jì)量,并且能夠得到方差估計(jì)。此外,我國(guó)移動(dòng)電話普及率逐年上升,在解決隨機(jī)撥號(hào)電話調(diào)查無回答的問題之后,應(yīng)該大力發(fā)展移動(dòng)電話調(diào)查。

