一種基于容錯和擾動補償的列車制動控制策略研究

馬得銀，常 懌

(洛陽鐵路信息工程學校，河南 洛陽 471000)

鐵路交通的迅速發展給研究人員和鐵路工業帶來新的挑戰，基于安全、快速和精確制動控制的列車自動控制系統成為研究熱點[1]。目前列車制動系統通常基于列車制動模型而設計，這種設計方法的好處在于能夠最大限度地對列車制動系統的優勢進行分析和利用，并結合模型近似求解的算法對列車制動過程進行仿真模擬，優化列車制動系統的性能[2-3]。但是在列車實際運行過程中，基于模型設計的列車制動系統需要面對一些不確定因素，如故障擾動和測量數據失真等，因此需要引入一些機制對這些擾動進行估計和補償，以提高列車制動系統運行的穩定性[4-5]。

文獻[6]針對列車制動系統經常發生的車輪阻塞干擾導致的制動距離和位置測量錯誤進行量化分析，并利用量化分析結果對測量傳感器的數據進行校正。文獻[7]基于對牽引控制系統中的傳感器進行分析，提出一種基于模糊數學的制動模型。文獻[8]在對列車進行故障診斷的基礎上，對列車制動系統進行故障補償，最大限度降低制動過程中意外因素對制動效果的影響。

通過對上述研究成果的分析，基于對列車制動過程中擾動因素的考慮，本文提出一種基于故障容錯和擾動補償的列車制動控制策略。該控制策略利用基于列車運行參數構建的理想化列車參照系統為制動控制系統提供目標控制值，并通過制動模型和容錯機制對測量數據的誤差以及故障干擾進行補償，采用基于PI控制器的閉環控制系統實現了具有較強抗故障干擾的列車制動控制模型。最后通過仿真分析對模型的有效性和抗干擾性能進行證明。

1 列車制動系統模型

1.1 列車故障模型

處于正常運動狀態中的列車其運動方程為[9]：

(1)

式中：v為速度，m/s；x為車輛的位置,m；w(v)為特定的外部阻力；b(v)為最大制動力；Ub為相對制動力；f(v)為特定的最大牽引力；Um為相對牽引力；g(x)為列車的一般外部阻力。

基于對外部擾動因素的考慮，對列車運動模型進行修正。首先對列車運動阻力之一的動態摩擦力進行近似估算[10]：

w(v)=w0+w1v+w2v2

(2)

式中：w0，w1，w2分別為靜態黏著系數、勻速黏著系數和加速度黏著系數。

u為制動或牽引系數，當u<0時表示制動系數，當u>0時表示牽引系數。

另外，列車運行過程中的一般外部阻力將被忽略。因此本文所討論的列車在進站時為行駛于平坦地面且處于能見度最大化的直線行駛過程中。

由上所述，在沒有故障的情況下列車運動的向量方程為[11]：

(3)

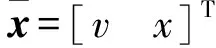
D(v)=[d(v) 0]T，d(v)=-w0-w2v2

(4)

列車在運動過程中的故障主要有制動器故障、系統故障或傳感器故障[12]。當列車開始制動時，這些故障就會對列車的制動性能產生影響。基于不同的故障類型，故障模型可以概括為以下3種形式。

第一種是帶有故障指示開關的混合制動系統。制動系統還未發生故障，且u<0，則制動系統故障模型如式(3)所示。

當制動系統已經發生故障，且u<0，則制動系統故障模型為：

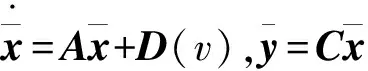
(5)

第二種是列車制動系統出現外部因素導致的故障。這種情況下，需要在列車模型中引入能夠表示外部故障特征項。

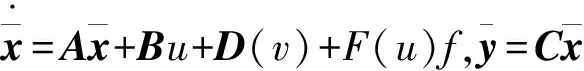
(6)

式中：F(u)f表示外部故障特征項，其中f表示外部故障發生的概率。如果u<0，則F(u)=-γBu；如果u>0，則F(u)=0。其中γ∈[0,1]，為故障對列車制動系統的影響程度。如果γ=1,則表示故障對列車制動系統具有全局性的影響，并且列車自動控制系統對制動系統失去控制。

第三種是傳感器故障。這種故障體現在故障模型的輸出中所增加的故障項。

(7)

1.2 制動控制系統架構

在實際應用中,動態摩擦的一部分力d(v)無法運用現有的傳感器技術實現精確測量，只能通過式(2)進行近似估算，因此有必要通過其他技術來提高估算的準確度[13]。鑒于此，本文提出一種通過構建輸入觀察器的方法來實現對動態摩擦力的測量。

另一個問題是當制動系統發生故障導致制動系統失去可控性時，列車自動控制系統不能根據常規控制策略進行動態摩擦補償[14]。

此外，如果由于車輪傳感器受到物理效應的干擾導致測量數據出現偏差，其結果是在列車接近下一個可校準位置數據的信標之前都不能獲取準確的列車實際位置軌跡。而列車位置誤差隨故障持續時間的增加而增大。因此需要盡可能快地檢測到所發生的故障,從而觸發控制動作，抑制故障，減少位置誤差[15-16]。

基于對上述實際問題的考慮，本文構建一個理想化的參照系統，為列車制動系統提供速度參考值以及準確的停車位置等控制器的目標值。隨后，設計了一個用于列車制動控制的PI閉環控制器，控制器的補償輸入為從速度觀測器所獲得的估計值。當列車速度觀察器的狀態收斂到近似列車系統的實際值時，控制器可以完全補償動態摩擦力，大幅提高制動控制系統的控制性能。為了檢測制動過程中的干擾故障，系統采用了一種基于測量速度和觀察器速度估計的差值發生器，對兩者差值進行濾波，如果濾波后的差值觸發了檢測閾值，就會認為出現制動故障，并通過禁用常規制動控制策略的方式來抑制故障。制動控制系統架構如圖1所示。

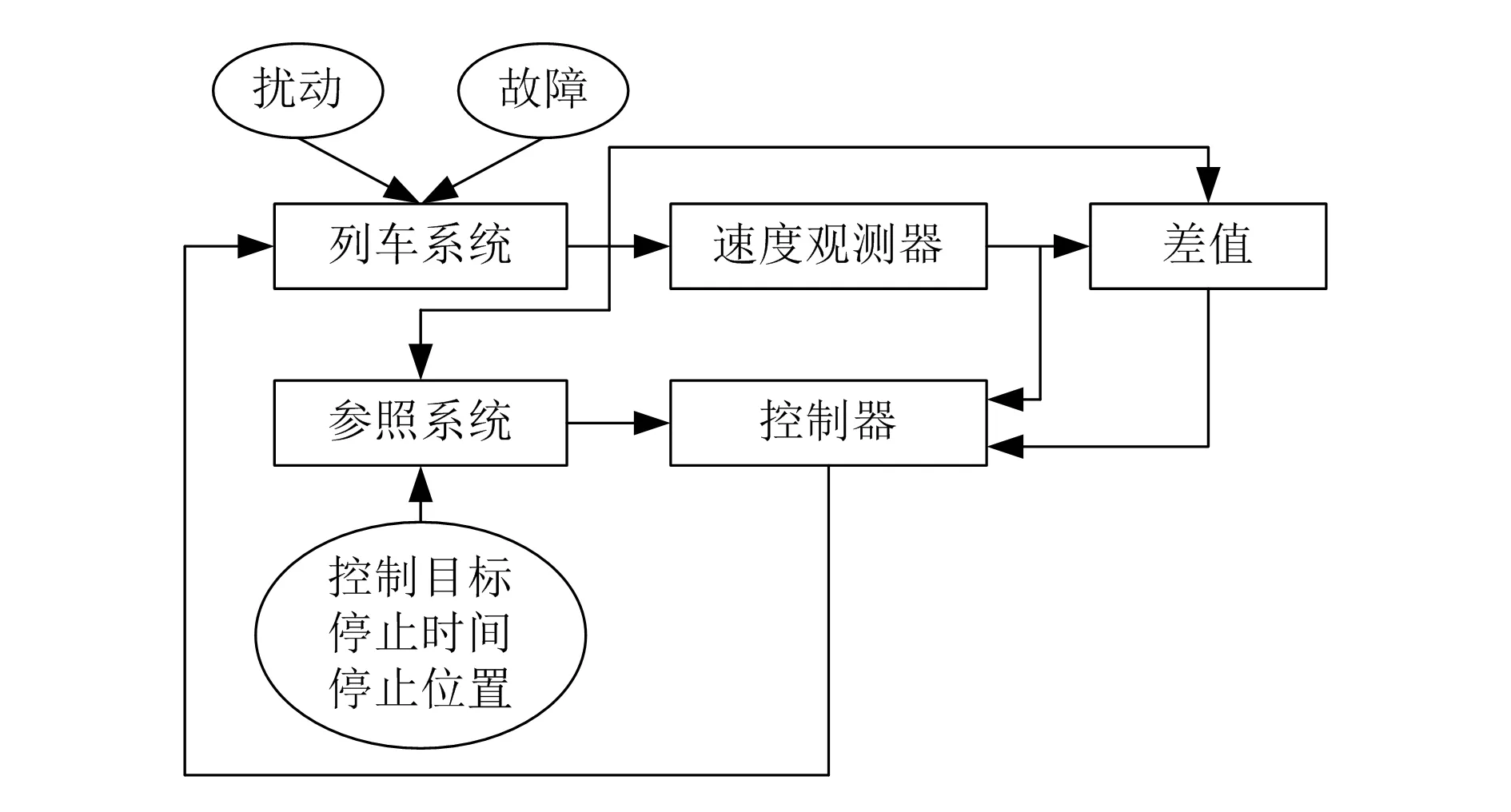
圖1 列車制動控制系統架構

2 模型計算

2.1 控制器

對列車制動系統的控制器而言，理想化的列車參照系統提供了列車系統的最終停止位置以及推薦的制動幅度等目標值。

列車參照系統的運動方程為：

(8)

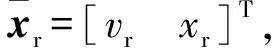
(9)

式中：t為制動過程的時間序列；t0為制動系統啟動的初始時間；v(0)為在t0時刻列車的速度。從式(9)中推導出列車理想的停止時間和停止位置：

(10)

(11)

式中：vmin為列車停止前的最小速度，通常等于0；x(0)為在t0時刻列車所在的位置。基于式(9)對式(8)中的控制參數u*進行計算：

(12)

參照系統的控制參數u*以及相關參數依據列車的實際位置和速度進行更新，為制動系統提供目標控制值。

為了減少參照系統和列車實際系統之間的差值，基于u*對控制參數進行優化計算：

(13)

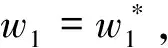
(14)

將式(13)代入式(14)，得出兩種故障情況下的輸入誤差。

第一種是靜態故障，其輸入誤差為：

(15)

第二種是動態故障，其輸入誤差為：

(16)

考慮到在誤差過大的情形下進行誤差補償是不可行的，因此需要容錯機制來保證制動系統的可靠性。該機制首先是禁用制動控制系統的功能，然后等到故障導致的誤差降到故障檢測閾值范圍以內再啟動制動控制系統。

2.2 觀測器

為補償制動系統的動態摩擦力，設計了一種基于無故障情況的輸入觀測器。

基于觀測器的設計對列車運動方程進行修改：

(17)

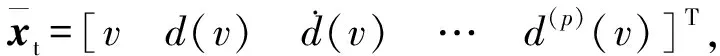
(18)

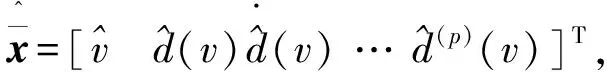
觀測器的速度估算值與基于傳感器的速度測量值的差值和確定的故障檢測閾值是觸發故障報警的根據。在實際系統中由于測量值的不確定性，因此需要采取一定的措施確保不會因測量誤差而觸發故障報警。故障檢測閾值的確定是一個多約束的問題，即最小概率的假警報、最小概率的誤報以及最快的檢測速度。對實際應用而言，最快的檢測速度下要能夠檢測出具有破壞影響的故障和可忽略、無關安全的檢測數據偏差，以確保可以根據差值的大小推斷出故障的影響程度，從而決定是否禁用自動制動控制系統。

3 仿真驗證

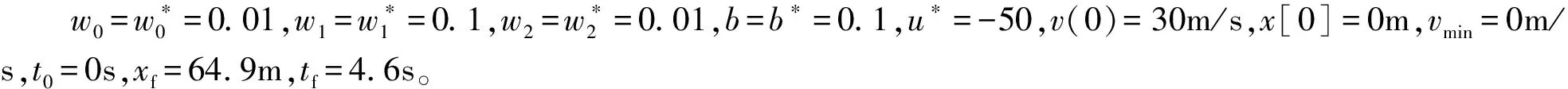
在無故障的情況下，列車停止位置的誤差對比如圖2所示。參照系統和仿真系統動態摩擦力的估計值d(v)的對比如圖3所示，控制信號的對比如圖4所示。

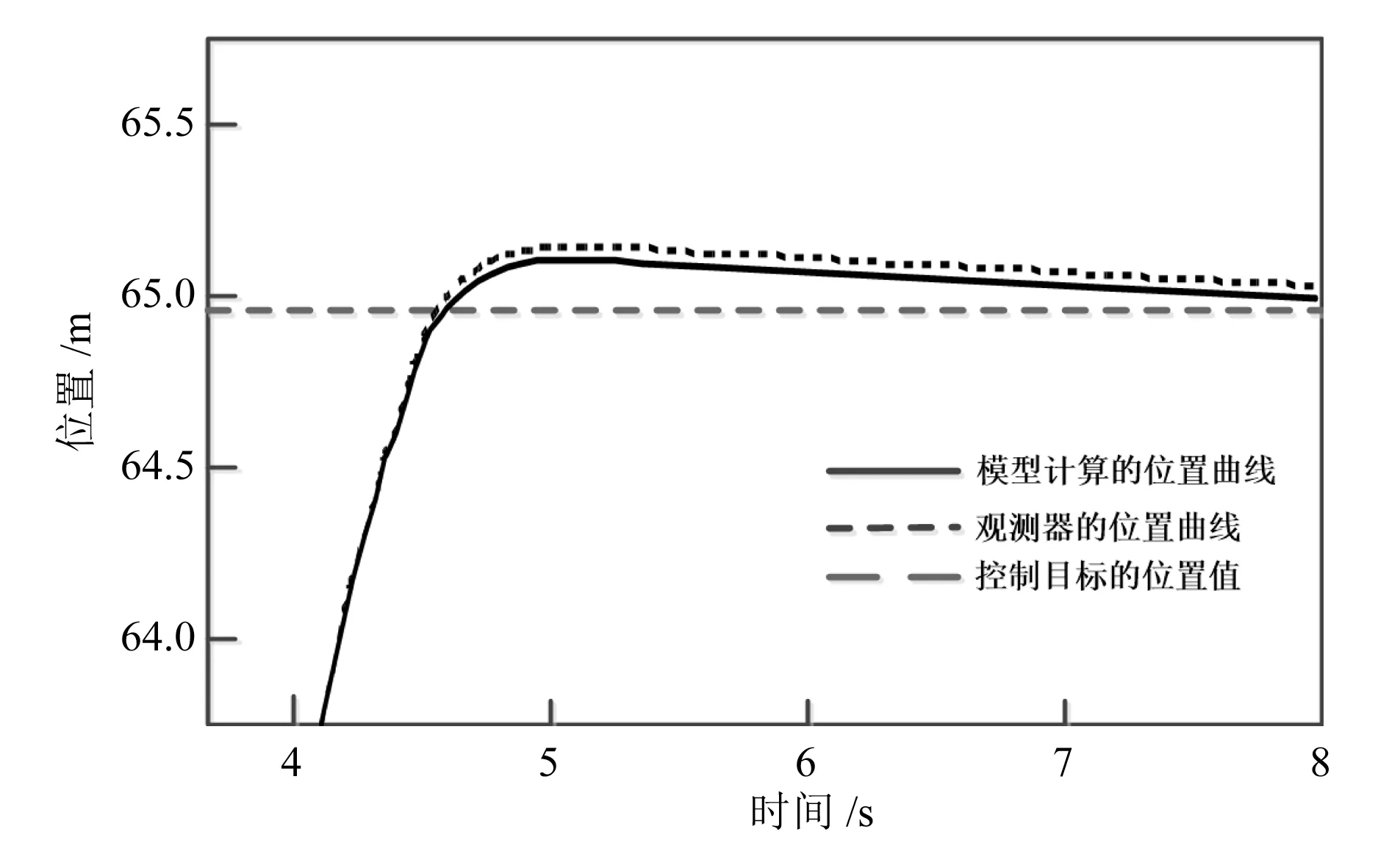
圖2 無故障情況下列車的停止位置對比

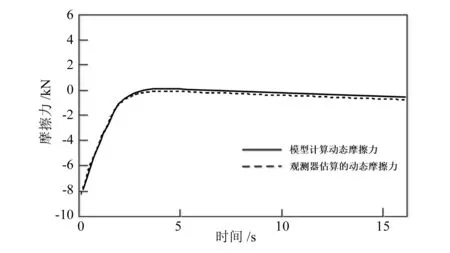
圖3 無故障情況下的動態摩擦力對比

圖4 無故障情況下的控制信號的對比

由圖2可知，列車在參照系統和仿真系統中的停止位置誤差為|x(tf)-xf|=0.061m，列車停止位置的精確度較高。圖3中的d(v)估計值較為準確，而圖4所示的控制信號曲線也較為平滑。

觀測器的速度估算值與基于傳感器的速度測量值差值曲線如圖5所示。

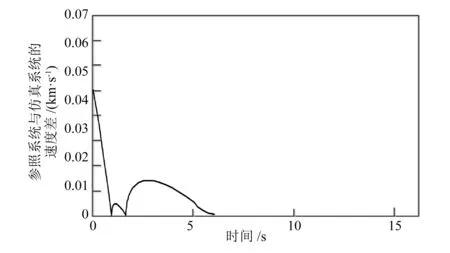
圖5 無故障情況下的速度差值曲線

由圖5可知，由于沒有故障擾動，經過短暫的波動之后差值快速收斂到零。

使用相同參數的仿真系統，在發生故障的情況下，采用本文所述的擾動補償控制策略對列車的制動控制進行仿真測試，測試數據見表1。表中對不同的故障持續時間以及故障檢測的時間延遲對最終位置誤差εp=|x(tf)-xf|(ltrain)-1的影響進行了對比。測試中設定故障閾值為0.05，ltrain(列車長度)為100m。

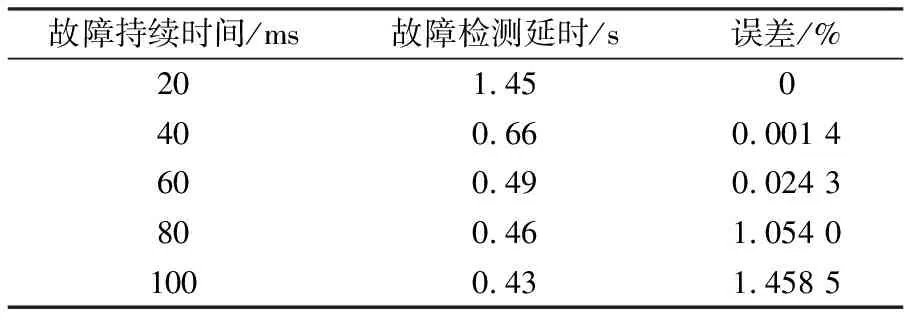
表1 不同故障持續時間的誤差對比

故障持續時間為20ms時的位置誤差對比曲線、控制信號曲線和速度差值曲線如圖6～圖8所示。

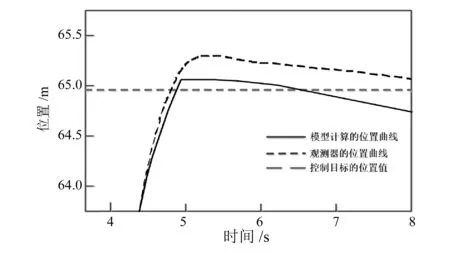
圖6 故障持續時間為20ms的位置誤差對比

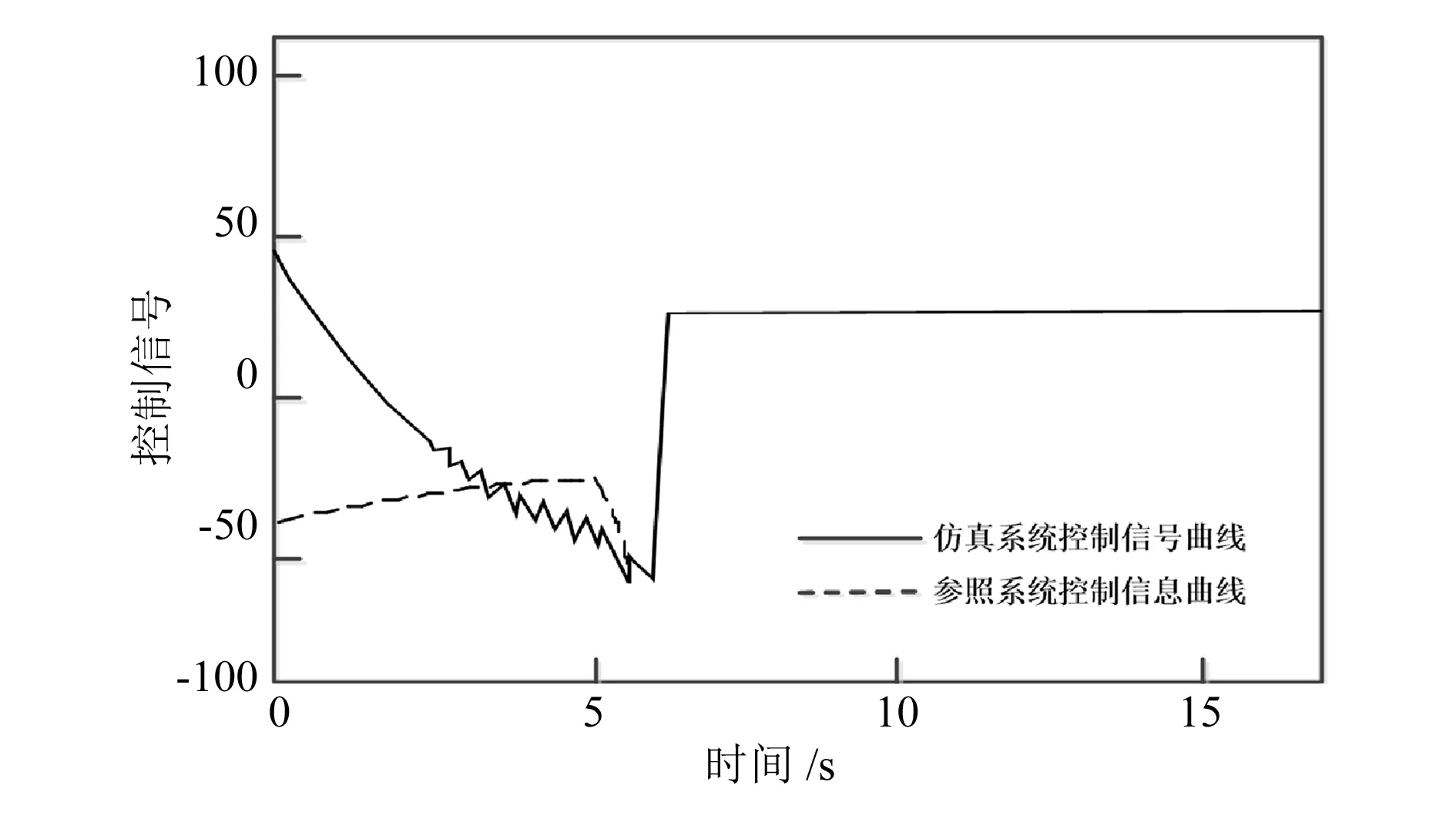
圖7 故障持續時間為20ms的控制信號曲線對比

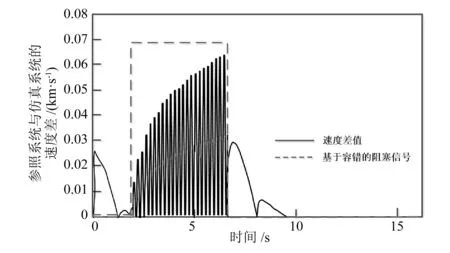
圖8 故障持續時間為20ms的速度差值和故障容錯曲線

由圖6可以看出，在20ms的持續故障的擾動下，列車的停止位置誤差只有0.01m。

故障持續時間為40ms時的控制信號曲線和速度差值曲線如圖9、圖10所示。

對比圖7和圖9，20ms持續故障擾動下的控制信號比40ms持續故障擾動下的控制信號具有更小的振蕩幅度。由圖8和圖10 可知，在速度差值幅度過大時，容錯機制開始發揮作用，自動制動控制系統被阻塞，直到差值降到閾值以下，自動制動控制系統才開始工作。

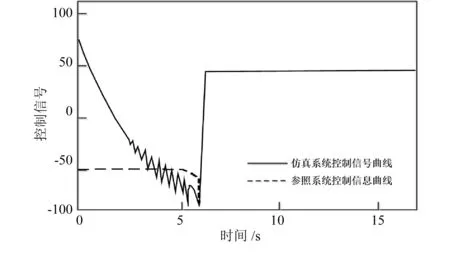
圖9 故障持續時間為40ms時的控制信號曲線對比

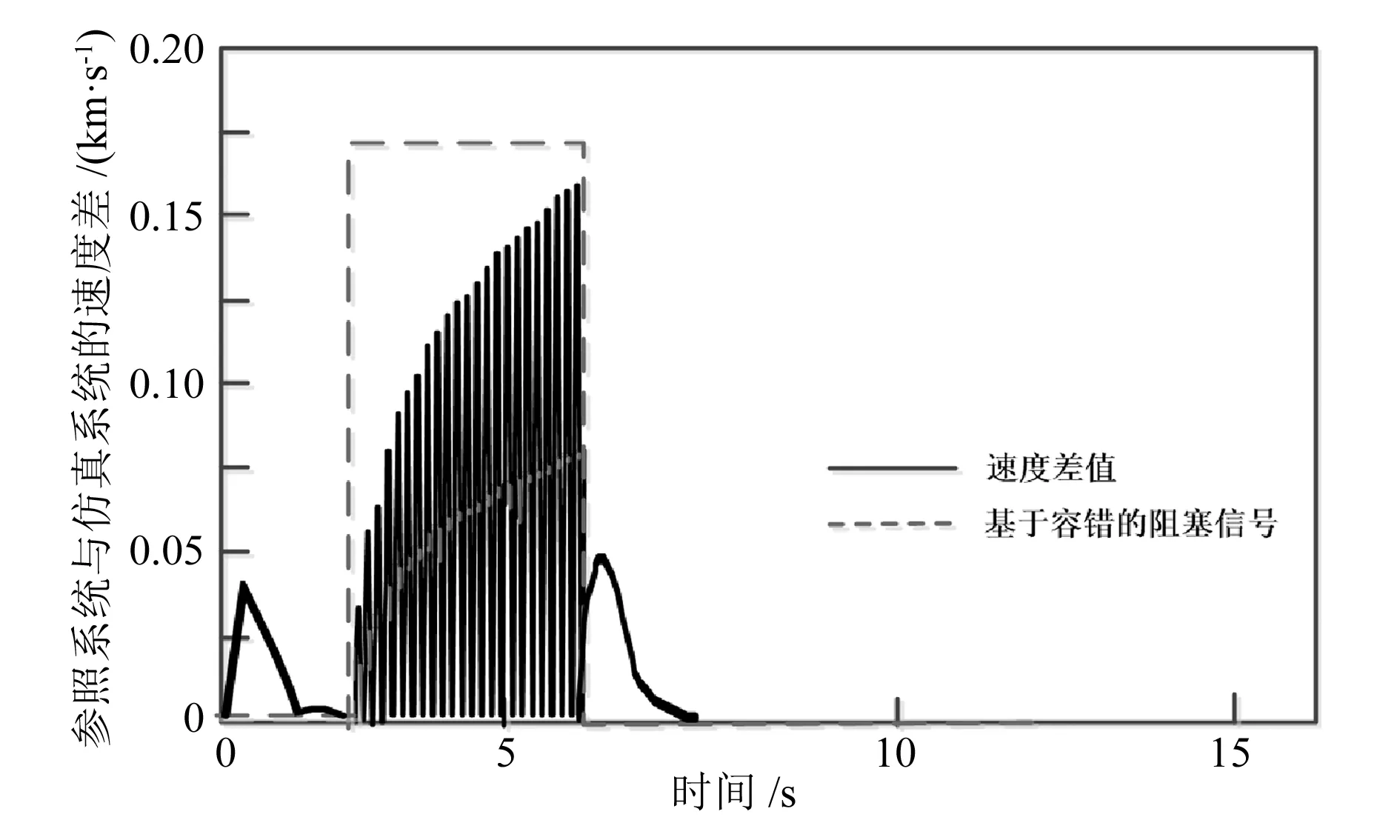
圖10 故障持續時間為40ms時

4 結束語

本文提出了一種具有較好抗干擾性能和容錯機制的列車制動控制系統模型。該模型包括故障檢測、擾動補償和容錯機制，對模型估算值和速度測量值的不確定性具有良好的魯棒性。通過仿真分析表明，該模型在不同故障持續時間和不同故障檢測延時情況下，都具有良好的制動性能。