一類不等式的巧思妙解

邊紅霞

(河北省易縣中學 074200)

函數與不等式是高考考查的重要內容，此類問題解決的基本途徑是，通過構造函數，將不等式問題轉化為函數問題，利用函數的性質,從而使問題得解.

例1 (2011年遼寧卷11題)函數f(x)的定義域為R，f(-1)=2，對任意的x∈R，f′(x)>2,則f(x)>2x+4的解集為( ).

A.(-1,1) B.(-1,+∞)

C.(-∞,-1) D.(-∞,+∞)

分析根據所求及導數不等式f′(x)>2的結構特點，構造函數g(x)=f(x)-2x-4(x∈R)，∵g′(x)=f′(x)-2，由條件f′(x)>2，則g′(x)>0，g(x)是增函數.又∵g(-1)=2+2-4=0，f(x)>2x-4的解集即為使得g(x)>0，即g(x)>g(-1)，由g(x)是增函數，∴x>-1，選B.

評析因為f′(x)>2，可以得到函數f(x)-2x是增函數，但所求不等式為f(x)>2x+4，因此函數f(x)-2x-4也為增函數，于是構造函數g(x)=f(x)-2x-4根據其單調性，脫去函數符號f，得到不等式的解.

題目所求為抽象不等式，沒有具體解析式，但是條件中有導數不等式，因此從條件出發，以所求為目標，鋪路搭橋，將所求不等式轉化為函數，利用函數的單調性，脫去函數的符號f，解決了不等式問題.

例2 設函數f′(x)是奇函數f(x)(x∈R)的導數，f(-1)=0,當x>0時，xf′(x)-f(x)<0，則使得f(x)>0成立的x的范圍是( ).

A.(-∞,-1)∪(0,1) B.(-1,0)∪(1,+∞)

C.(-∞,-1)∪(-1,0) D.(0.1)∪(1,+∞)

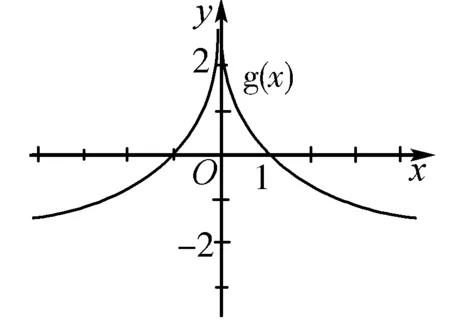
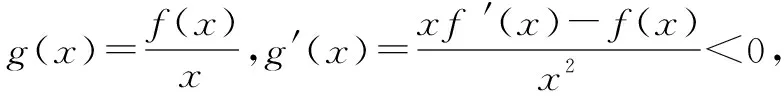
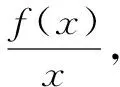
函數、方程、不等式之間有密切的聯系，往往相互轉化，三者以函數為中心，達成求解意向，并且在解決的過程中，函數的性質和圖象又會提供豐富的資源，使問題的解答更加巧妙.這道題充分利用了函數的奇偶性，通過數形結合，將問題直觀形象地表達出來，從而迅速得解.

例3 已知定義在R上的函數f(x)的導函數為f′(x)，對任意的x∈R滿足f′(x)-f(x)<0，則下列結論正確的是( ).

A.2f(ln2)>3f(ln3) B.2f(ln2)<3f(ln3)

C.3f(ln2)>2f(ln3) D.3f(ln2)<2f(ln3)

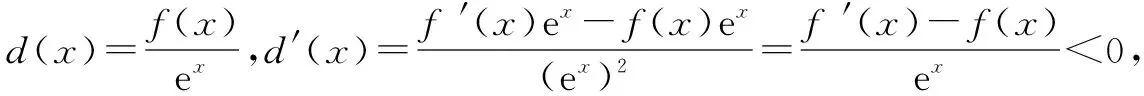
故選C.

例4 定義在R上的函數f(x)，導函數是f′(x)，若f′(x)+f(x)>1,f(0)=2018，則不等式exf(x)>ex+2017(其中e為自然對數的底數)的解集是 .

分析構造函數g(x)=exf(x)-ex-2017，∴g′(x)=exf(x)+exf′(x)-ex=ex(f(x)+f′(x))-ex>0，∴g(x)是增函數，而g(0)=e0f(0)-e0-2017=0，∴x>0時，g(x)>0,即exf(x)>ex+2017，故答案為(0，+∞).

評析所求不等式中有函數exf(x)，其導數為ex(f(x)+f′(x))，從而聯想構造函數，g(x)=exf(x)-ex-2017，這樣將條件和所求取得聯系，利用函數的單調性求解.

在解決問題的過程中，為了充分利用條件，要對條件和結論進行恒等變形，通過發展條件，轉化結論，拉近已知與所求的距離，使他們形成有效對接，達到解題目的.本題就是將結論進行轉化，形成兩個函數值比較大小的結構，從而構造函數，再通過導數不等式，確定函數的單調性，利用函數的單調性得以解決.

從以上可以看出，在解決數學問題時，要樹立目標意識，咬定目標不放松，善于對題目進行整體分析，并把已知作為基本素材，搭建向目標邁進的橋梁，在前進的路途中，要有大局意識，綜合考量，偶遇險灘，也不必驚慌，時刻把準方向，以基本技能為槳，以所學知識為綱，這樣便能夠順利到達題目的彼岸!