MATLAB軟件在數值分析課程中的應用

牛瀟萌

1 引言

數值分析是研究數據結構和數量關系的數學分支，在信息與計算科學、物理學、數學與應用數學等專業的教學中都是一門很重要的專業課.其內容包括插值方法、數值積分、數值微分、常微分方程的差分方法、方程求根的迭代法，線性方程組的迭代法和線性方程組的直接法等.

在許多情況下，要獲得精確解是十分困難的，有時是不可能的，例如，由于找不到的原函數，所以用牛頓-萊布尼茨公式就不能求解定積分到因此研究各種數學問題的近似解變得非常重要了，數值分析就是專門研究各種數學問題的近似解的一門課程.因而數值分析是現代計算科學的必要理論基礎，作為數學與應用數學專業選修課，數值分析對學習其它專業課是必不可少的.

《數值分析》課程學習的主要困難在運算過程、運算公式復雜，不能簡單的靠一支筆就能算出來，而需要通過計算機來執行運算[1-3].本文將以《數值分析》課本中一些容易實現的例子來說明MATLAB在《數值分析》課程教學過程中的重要應用.

2 數值分析實驗步驟

數值分析課本中有很多流程圖，需要上機實驗，在數值分析課程的實驗教學中可以讓學生按如下步驟做數值分析實驗并寫出數值分析實驗報告：

（1）算法描述；

（2）編寫算法實現的M文件；

（3）用具體實例運行M文件，得出運行結果或者圖形.

下面以秦九韶算法為例，讓學生對數值分析上機實驗有所了解.

（1）秦九韶算法的公式[4]

（2）算法流程圖

（3）秦九韶算法實現的M文件

根據上述流程圖，用MATLAB編寫算法的M文件，代碼如下：

function v=qinjiushao(x,a)

%其中a是多項式的系數

[hang,lie]=size(a);

n=lie;

v=a(n);

k=1;

while k～=n

v=x*v+a(n-k);

k=k+1;

end

（4）用具體實例運行M文件，得出運行結果

利用編寫的M文件計算如下多項式：

在x=3處的值.

在MATLAB命令窗口輸入如下命令

x=3;a=[1-1 4 0-3 1];

qinjiushao(x,a)

得到結果是34.

3 利用MATALB軟件將數值分析課程教學直觀化

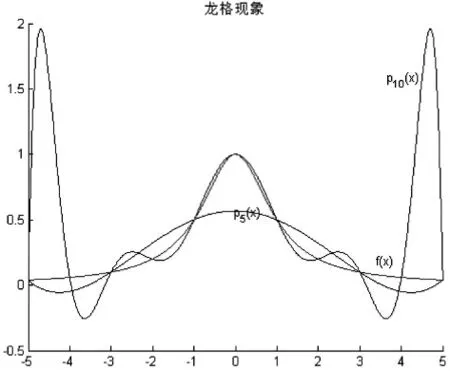
數值分析課程中有許多例子比較抽象，難于理解，教師可以利用MATALB強大的繪圖功能，將這些例子直觀化，便于學生理解，加深印象.下面以高次插值的龍格現象說明此問題.

在講解高次插值的龍格現象時，教師可以用MATLAB編寫程序演示，讓學生直觀上認識到隨著插值節點的增加，高次插值多項式的逼近效果有時是不理想的.考慮如下函數

首先編寫如下M文件:

function f=myrunge(i)

x=linspace(-5,5,i);

y=1./(1+x.^2);

p=polyfit(x,y,i-1);

xx=-5:0.01:5;

yy=polyval(p,xx);

plot(xx,yy);

其次在區間[-5,5]內取6個節點和11個節點來畫圖，驗證龍格現象.

hold on

myrunge(6)

gtext('p_5(x)')

myrunge(11)

gtext('p_{10}(x)')

xx=-5:0.01:5;

plot(xx,1./(1+xx.^2),'r')

gtext('f(x)')

title('龍格現象')

得到如下圖像.

4 結論

本文通過數值分析課本上的幾個例子，給出了MATLAB軟件在數值分析教學過程中的應用.數值分析教學過程中使用MATALB軟件可以解決教學過程中很多題目無法手算的難題.這也有助于培養學生的編程能力，將數值分析應用到實際問題中的能力.