輸流曲管面內振動的小波有限元方法研究
曹建華, 劉永壽, 劉 偉
(1.西北工業大學 力學與土木建筑學院,西安 710029;2.黃山學院 機電工程學院,安徽 黃山 245021)
在現代工業中,輸流管道應用非常廣泛,振動現象引起了許多學者的研究,取得了很多的成果。大部分文獻集中在輸流直管的研究[1],而曲管相對較少。Svetlitskii[2]首先采用繩索模型研究輸流曲管面外振動。Chen[3-5]在曲管研究方向作出巨大的貢獻。他分別用牛頓法和哈密頓法推導了曲管的面內振動微分方程,并利用哈密頓方法推導了面外振動微分方程。他發現兩端固定端的和簡支的曲管,當流速超過某一臨界值時,發現屈曲。Hill等[6]研究了諸如環形、S開、L形和螺旋形輸流曲管的振動穩定性。Misra等[7-8]在前人的基礎上,重新細致研究了輸流曲管的振動穩定性,并將曲管研究分成三類:軸線不可伸縮理論、軸線不可伸縮修正理論和軸線可伸縮理論,并采用傳統有限元進行求解振動問題。Jung等[9-10]采用一種新的流速表達式,采用哈密頓法推導了輸流曲管面內和面外振動微分方程,并與由其他流速表達式所導出的方程相比較。Ni等[11-12]在曲管計算方法和非線性動力研究上作出了卓越的貢獻,他們利用微分積分法研究了輸流曲管在非線性約束下的動力學行為。Wang等[13]研究了廣義微分積分法(GDQR)在曲管面內振動的應用。
在文獻中,輸流管道振動微分方程的求解方法有很多種,傳遞矩陣法[14],伽遼金法[15],有限差分法[16],波動法[17],微分積分法(DQM)和有限元法。在諸多文獻中,有限元方法是應用較多的。在有限元方法中,選擇插值函數最為關鍵。由于小波緊支撐、光滑和對稱特性,小波用于數值計算,越來越受到關注。Chen等[18]采用Daubechies小波,構建薄板單元,以及應用于求解熱傳遞問題。Han等[19]分別應用2階和4階樣條小波尺度函數構建了薄板單元。Xiang等[20]采用埃爾米特區間樣條小波構建軸單元,Zhong等[21]分別采用2階和4階樣條小波函數構建了彈性實體單元。
本文首先在Misra所推導的公式基礎上簡化輸流曲管微分方程,然后簡述樣條小波理論,利用區間樣條小波作為插值函數,建立尺度為4,階數為6的區間樣條小波BSWI64新型輸流曲管單元,并用于離散曲管面內振動方程,最后求解直管和曲管面內振動問題,并將仿真結果與前人的文獻對比,驗證小波有限元方法的精度。
1 輸流曲管的面內振動微分方程
如圖1所示曲管,據Paidoussis和Misra可知,若無管外流體影響,輸流曲管的面內振動無量綱微分方程可簡化如下
(1)
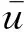
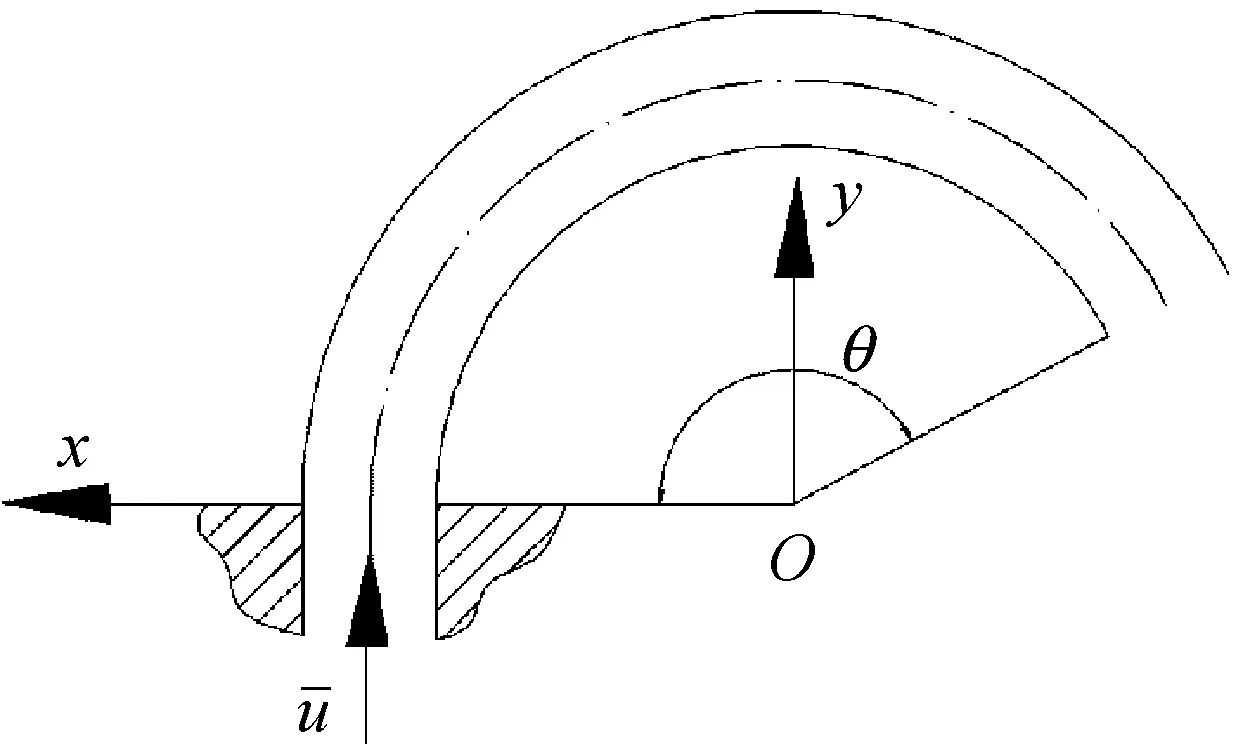
圖1 曲管模型Fig.1 The geometry of a curved pipe
輸流曲管兩種邊界條件分別為
2 輸流曲管的小波有限元
本節首先簡述樣條小波尺度函數的定義,選取尺度為4、階數為6的樣條小波尺度函數作為有限元的插值函數,最后根據傳統有限元的過程,用小波有限元離散式(1),推導小波有限元矩陣。
2.1 樣條小波尺度函數
區間[0,1]的B-樣條定義如下:序列點
j∈N0(自然數),B-樣條函數表達式為
(2)
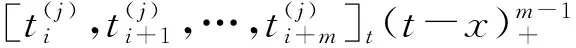
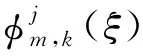

(3)
因此,在區間[0,1]上樣條小波的尺度函數可寫成向量形式
(4)
其中ξ∈[0,1][0,1],且2j0≥2m-1
在本文中, 小波有限元求解采用BSWI64樣條小波尺度函數作為插值函數,BSWI64樣條小波尺度函數如圖2所示。
2.2 輸流曲管的小波有限元格式
采用樣條小波尺度函數作為位移場的插值函數,其位移場函數η(ξ)可表示為
(5)
其中:
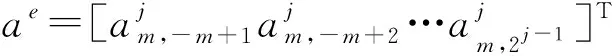
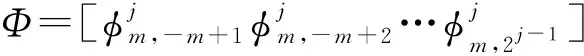
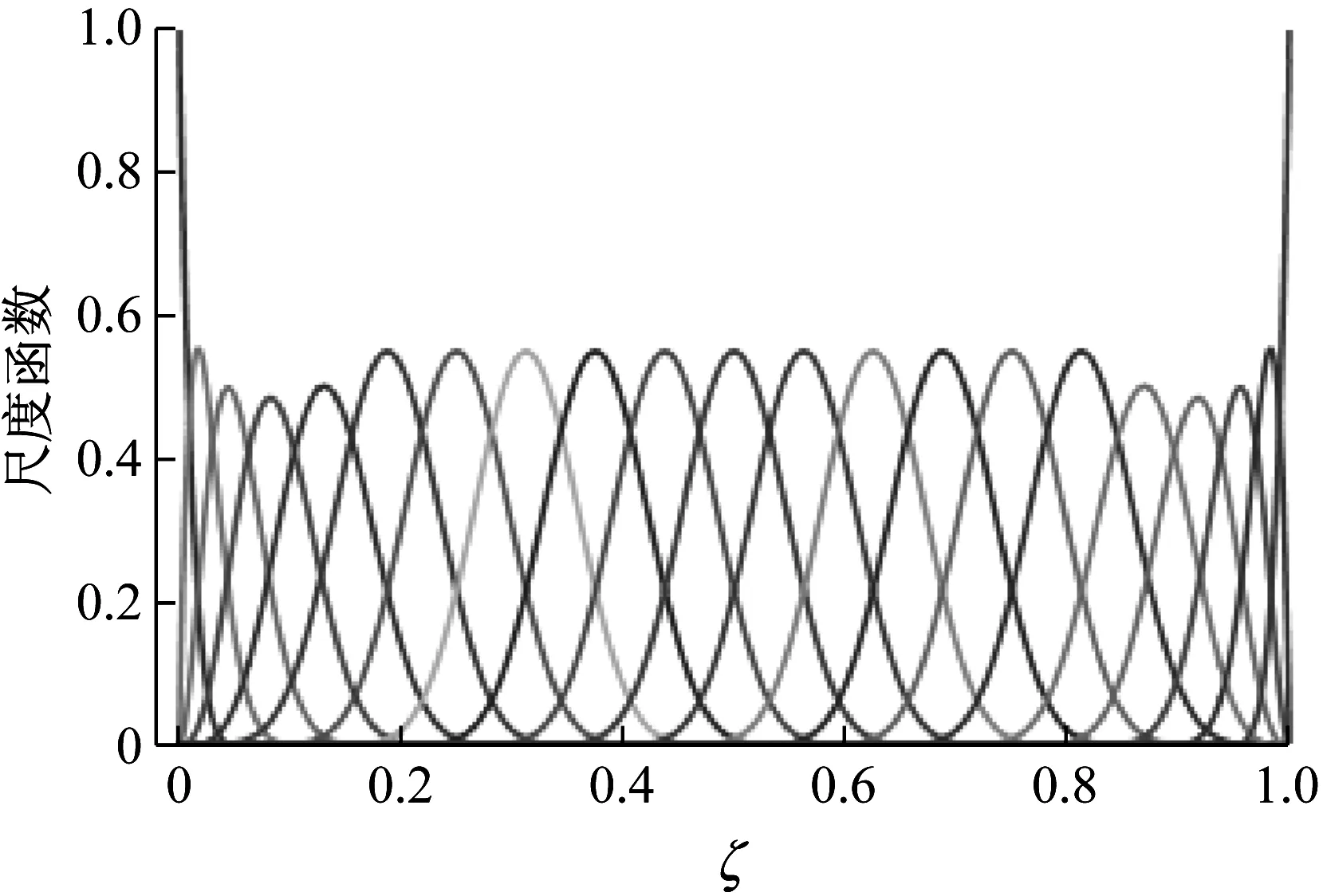
圖2 區間[0,1]的BSWI64的尺度函數Fig.2 The scaling function of BSWI64 in the interval[0,1]
定義單元物理自由度ηe為
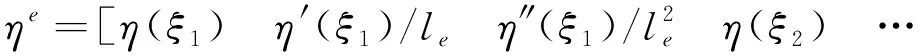
(6)
其中le為單元長度,ξi=(i-1)/2j,i=1,…,2j+1。
將式(5)中不同節點的η(ξi)分別代入(6)式,可以得到
ηe=Reae
(7)
其中,
(8)
將式(7)代入式(5)
η(ξ)=Φ(Re)-1ηe=Nηe
(9)
其中N=Φ(Re)-1是形函數向量。
采用傳統有限元方法過程,將式(1)進行離散,得到單元矩陣,單元離散方程如下
(10)
其中小波單元質量矩陣、小波單元阻尼矩陣和小波單元剛度矩陣分別為

(11)
(12)
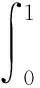
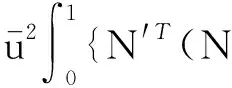
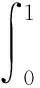
(13)
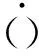
采用傳統有限元組合程序,可以得到系統矩陣,比如系統質量矩陣Mg,系統阻尼矩陣Cg,系統剛度矩陣Kg和系統位移向量η(t),其全局離散方程如下
(14)
3 數值算例
本節首先采用上述方法計算輸流直管,并與伽遼金法、傳統有限元方法相比較,然后分別求解基于軸線不可伸縮和基于修正軸線不可伸縮的輸流曲管例子,并與Misra所得的數值結果對比。
3.1 輸流直管算例
采用曲管單元計算直管的固有頻率,將Θ和Πo設為0,即為直管模型,以此模型來計算直管。如表1所示,列出三種方法(伽遼金法,傳統有限元,小波有限元法),計算四種不同邊界條件(兩端固定、一端固定一端簡支、一端固定一端自由、兩端簡支)的輸流直管的前5階無量綱固有頻率的數值結果。伽遼金方法采用六階,傳統有限元采用6個單元,而小波有限元僅用一個單元。從數值對比可以看出,小波有限元計算結果與其它兩種方法所得結果差別不大。
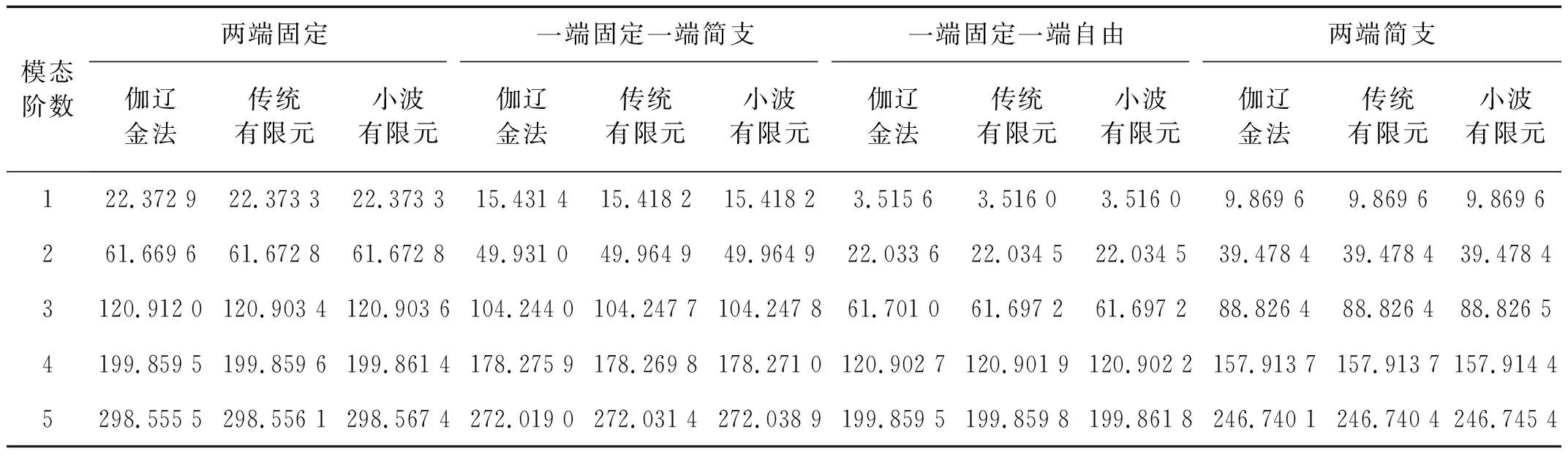
表1 輸流直管的無量綱固有頻率Tab.1 The natural frequency of fluid-conveying straight pipe
3.2 Πo=0時輸流曲管的數值算例
令Πo=0和β=0.5時,采用傳統有限元和樣條小波有限元,分別計算半圓輸流曲管在三種邊界條件(兩端固端,一端固定一端簡支,兩端簡支)下的前四階頻率實部隨流體速度變化,并進行對比。傳統有限元采用12個單元,小波有限元采用1個單元。由圖3~圖5可知,隨著流速的增大,每階頻率都在減小,一直減小至0,且兩種方法的計算結果吻合較好。
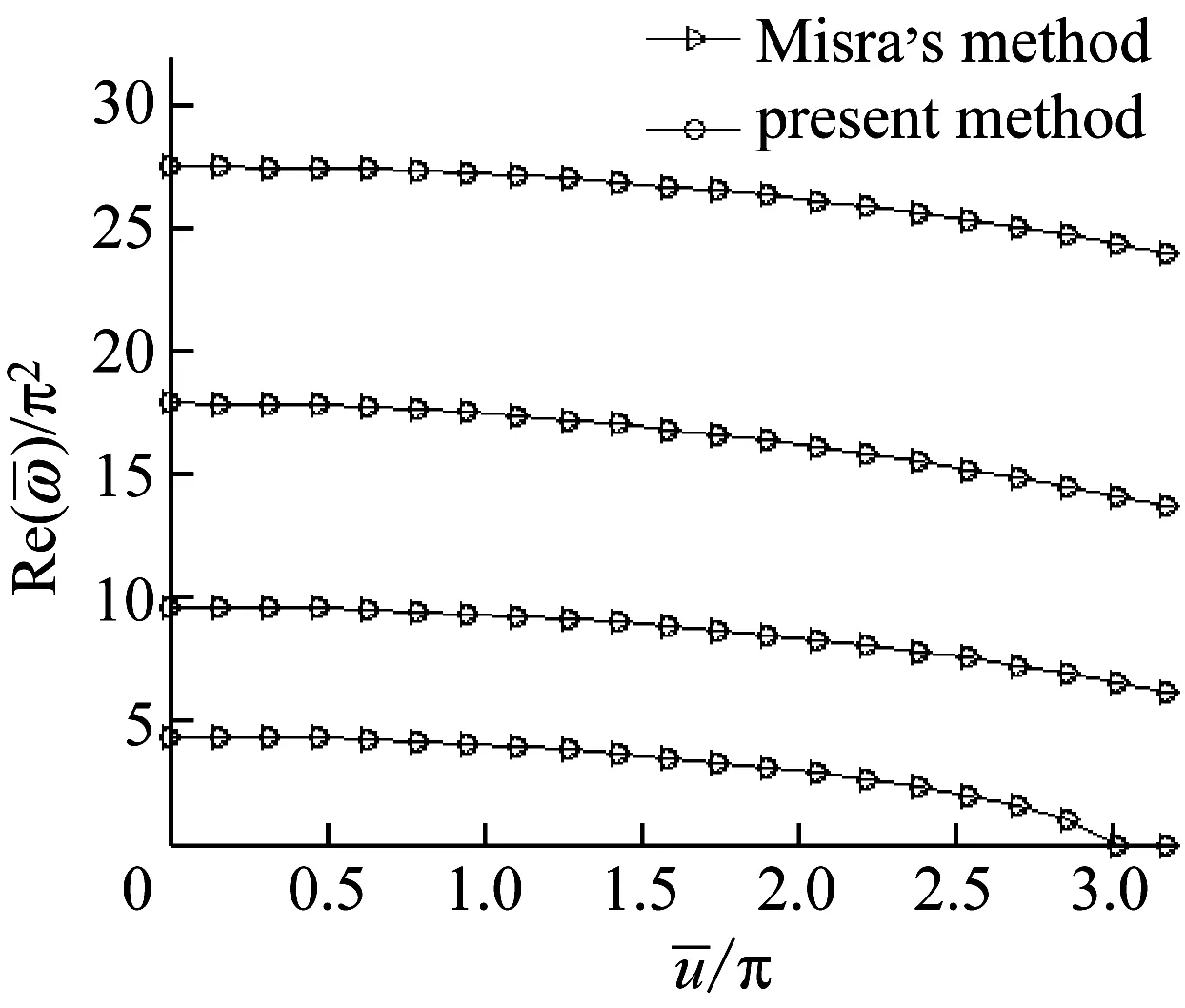
圖3 兩端固定的半圓形輸流曲管前四階頻率實部隨流速變化曲線(Πo=0)
Fig.3 Dimensionless frequencies of a fluid-conveying semi-circular pipe with two fixed ends as a function of flow velocity (Πo=0)
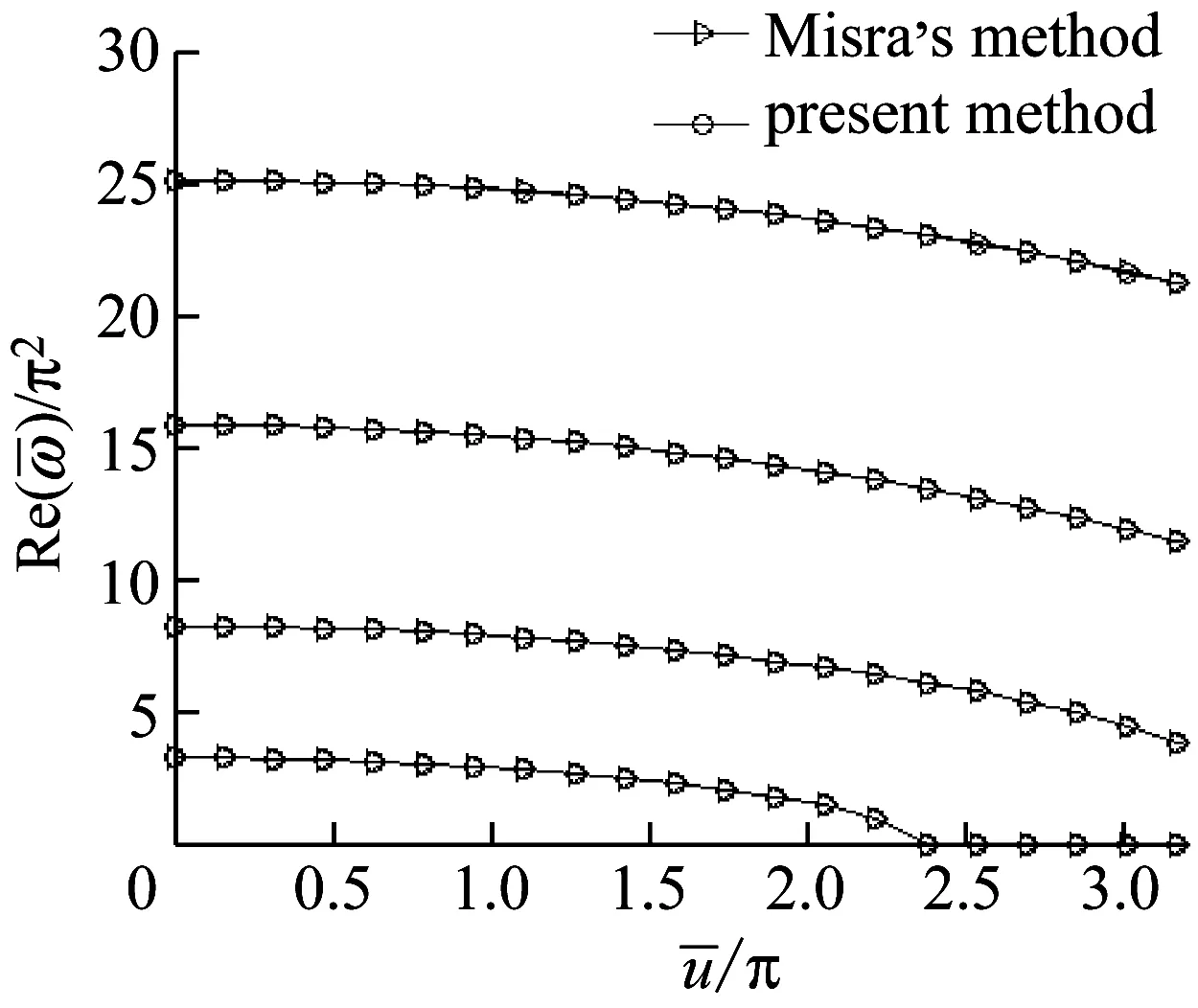
圖4 一端固定,一端簡支的半圓形輸流曲管前四階頻率實部隨流速變化曲線(Πo=0)
Fig.4 Dimensionless frequencies of a fluid-conveying semi-circular pipe with one fixed end and one simply supported end as a function of flow velocity (Πo=0)
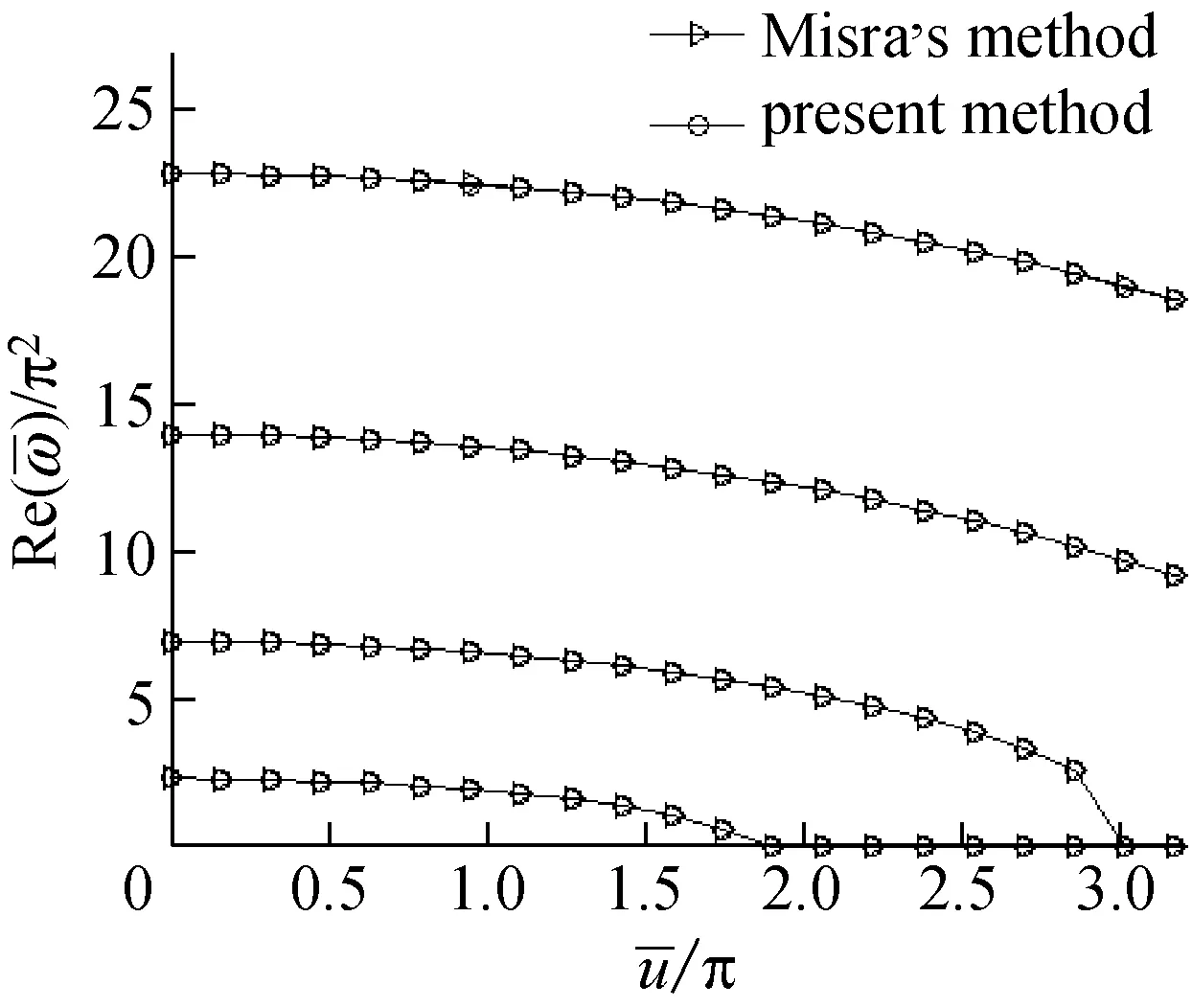
圖5 兩端簡支的半圓形輸流曲管前四階頻率實部隨流速變化曲線(Πo=0)
Fig.5 Dimensionless frequencies of a fluid-conveying semi-circular pipe with two simply supported ends as a function of flow velocity (Πo=0)
3.3 Πo≠0時輸流曲管的數值算例
令Πo≠0和β=0.5時,采用傳統有限元和樣條小波有限元,分別計算半圓輸流曲管在三種邊界條件(兩端固端,一端固定一端簡支,兩端簡支)下的前四階頻率實部隨流體速度變化,并進行對比。傳統有限元采用12個單元,而小波有限元采用1個單元。從圖6~圖8可以看出,隨著流速的增大,前三階頻率實部都在緩慢減小,一直減小,與軸線不可伸縮模型不同的是,但第四階頻率實部在增長,且兩種方法的計算結果吻合。
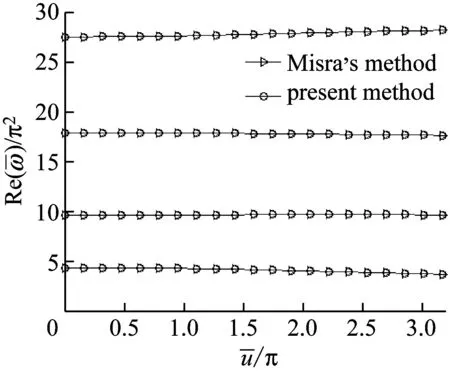
圖6 兩端固定的半圓形輸流曲管前四階頻率實部隨流速變化曲線(Πo≠0)
Fig.6 Dimensionless frequencies of a fluid-conveying semi-circular pipe with two fixed ends as a function of flow velocity (Πo≠0)
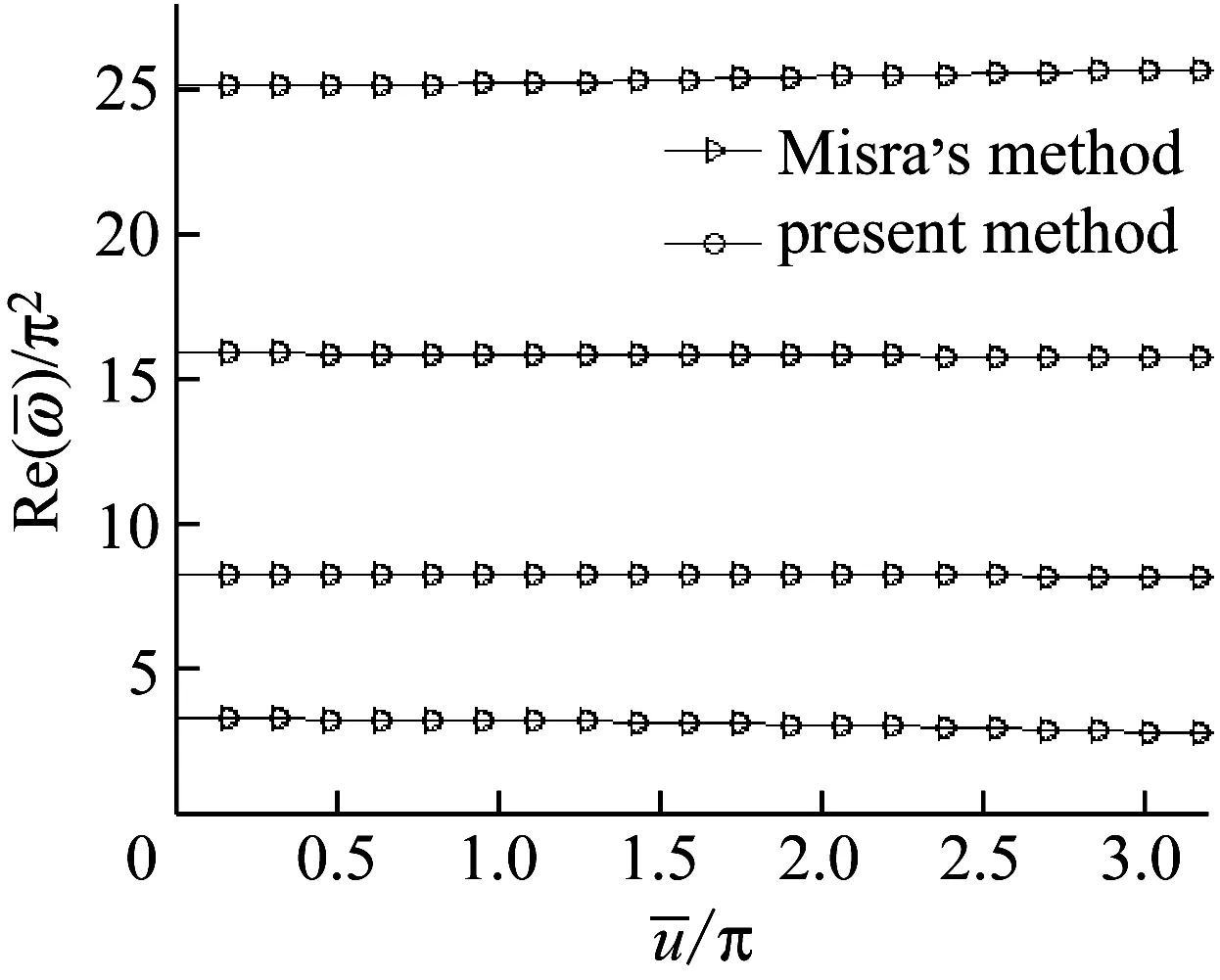
圖7 一端固定,一端簡支的半圓形輸流曲管前四階頻率實部隨流速變化曲線(Πo≠0)
Fig.7 Dimensionless frequencies of a fluid-conveying semi-circular pipe with one fixed end and one simply supported end as a function of flow velocity (Πo≠0)
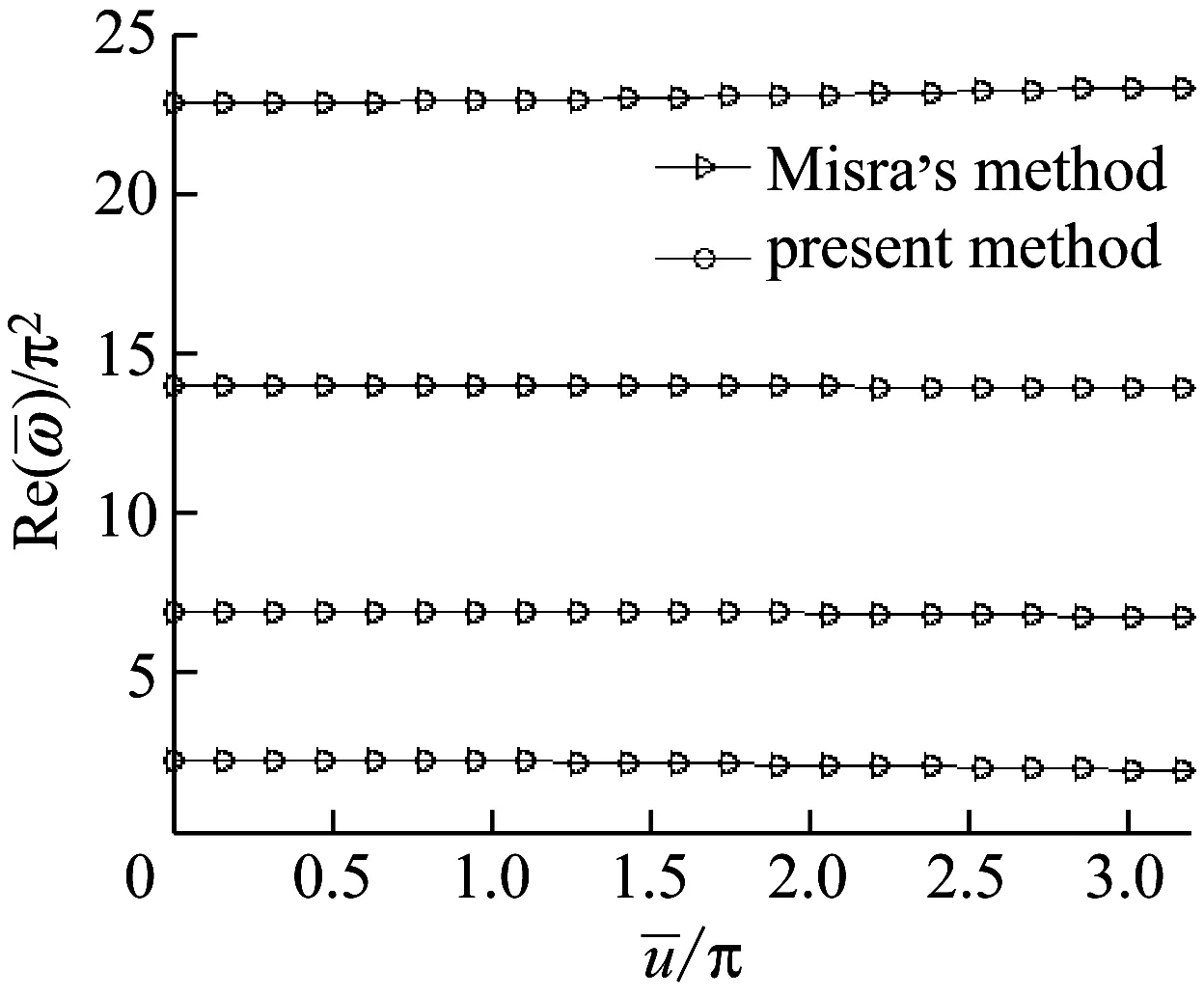
圖8 兩端簡支的半圓形輸流曲管前四階頻率實部隨流速變化曲線(Πo≠0)
Fig.8 Dimensionless frequencies of a fluid-conveying semi-circular pipe with two simply supported ends as a function of flow velocity (Πo≠0)
4 結 論
針對輸流曲管面內流致振動的無量綱控制微分方程,采用尺度為4,階數為6的區間樣條小波尺度函數作為位移場的插值函數,建立了新型小波輸流曲管單元,列出了小波單元質量矩陣、小波單元剛度矩陣和小波單元阻尼矩陣,應用于求解輸流直管和曲管流致振動問題。
通過數值結果對比,在求解輸流直管頻率上,與伽遼金方法、傳統有限元方法的所得結果對比,差別不大;在分別求解兩種理論模型下的輸流曲管頻率實部隨流速變化的曲線上,小波有限元與傳統有限元所得結果非常吻合,所得曲線幾乎重合。在計算過程中,小波有限元僅采用一個單元,計算時間短,數值結果可靠。
綜上所述,新型小波曲管單元在求解輸流曲管面內線性振動問題有一定的優勢,而在曲管非線性振動的應用上,需要進一步的研究。

