半變系數模型的幾乎無偏嶺估計探討

曹連英，王 蕾，張 博，徐文科

（東北林業大學 理學院，哈爾濱 150040）

0 引言

考慮如下的半變系數模型：

其中，y是響應變量，(xT，zT，u)是相應的協變量，xT=(x1，x2，…，xp)，zT=(z1，z2，…，zq)，u為時間變量或空間變量，為研究方便，本文假定u為一維變量；β=(β1，β2，…，βp)T為未知常值參數，α(·)=(α1(·)，α2(·)，…，αq(·))T為未知函數。ε為隨機誤差，滿足E(ε|xT，zT，u)=0和Var(ε|xT，zT，u)=σ2。

半變系數模型，因其含有部分線性模型，使之與非參數回歸模型比較具有更好地外延性；又因其變系數部分能充分體現協變量對響應變量在時間或空間上影響的差異性，使之與線性回歸模型相比有更強的靈活性。使半變系數模型受到相關學者的廣泛關注，已經提出了大量有價值的估計方法[1-5]，如：小波估計法[1]、局部多項式擬合方法[2]、一般級數方法[4]、輪廓最小二乘估計法[5]等。然而已有研究中直接或間接假設協變量xT=(x1，x2，…，xp)的系數矩陣列滿秩，即不具有復共線性。而實際問題中會遇到多重共線性問題，即xT的系數矩陣是病態矩陣，或者是非列滿秩的，這時利用一般的方法所得到估計結果的某些分量方差很大，使得估計值的精確度變差，甚至可能導致某些變量系數的估值正負符號與實際問題意義不符。對于病態或秩虧的線性回歸模型已經開展了深入研究[6，7]，其中嶺估計方法是有效解決這一問題并且使用廣泛的一種有偏估計方法。近幾年來，嶺估計方法被逐步應用到非線性回歸模型中。本文基于輪廓最小二乘方法給出半變系數模型的嶺估計和幾乎無偏嶺估計。

1 半變系數模型的嶺估計和幾乎無偏嶺估計

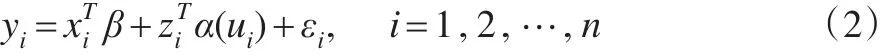
假定模型（2）中p維待估參數β已知 ，記，則模型（2）可寫成如下的變系數模型：

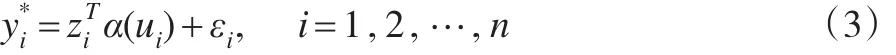
利用局部多項式擬合方法來估計變系數未知函數{αj(·)，j=1，2，…，q}。對給定u0附近的一點u，對αj(u)利用Taylor展開有：

應用局部加權最小二乘極小化：

其中Kh(·)為給定的核函數，Kh(·)=K(·/h)/h，h為帶寬。即可得到的估計。

為便于敘述，本文引入一些記號：

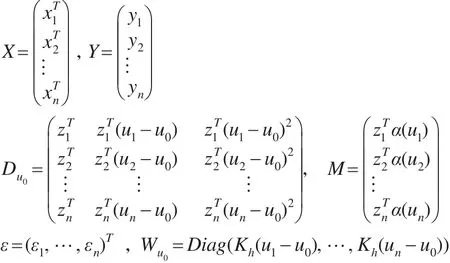
則模型(3)的矩陣形式為：

利用輪廓最小二乘估計方法可得α1(u0)，…，αq(u0)，的估計為：

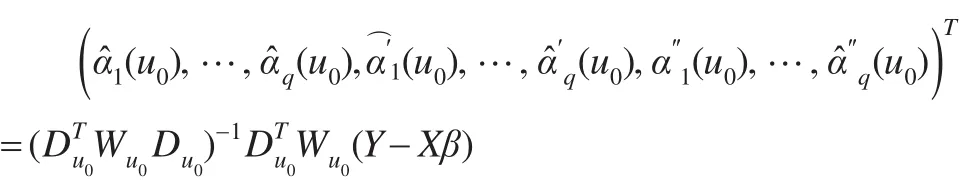
取u=u，得未知系數函數α(u)=(α(u)，…，α(u))T的

0i10q0估計：

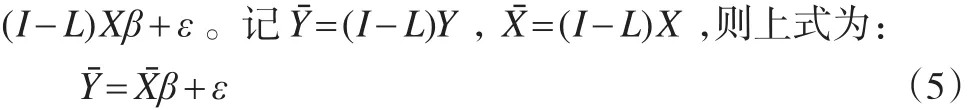
若模型(1)中協變量xT存在復共線性問題，會導致模型(5)中的接近奇異，從而β的輪廓最小二乘估計不能很好地解釋實際問題。為此本文引入半變系數模型的嶺估計方法[8]，并將嶺估計方法進行改進。

為研究方便，令Φ=(Φ1，Φ2，…，Φp)為正交矩陣，滿足即有偏強的復共線性性。記，模型（5）為：

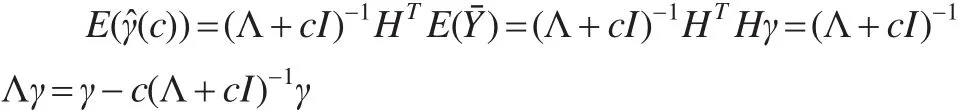
將模型(6)的嶺估計修正為：

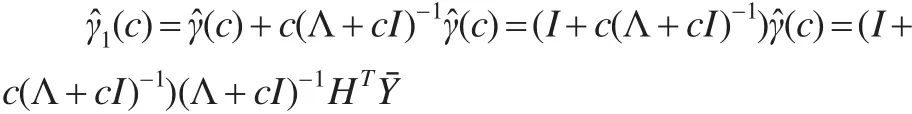
則模型(5)的參數部分系數的幾乎無偏嶺估計為：

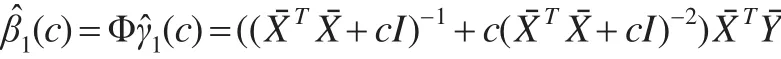
變系數函數在ui處的估計α(ui)為：

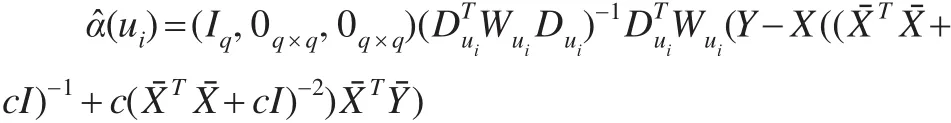
2 幾乎無偏嶺估計的性質

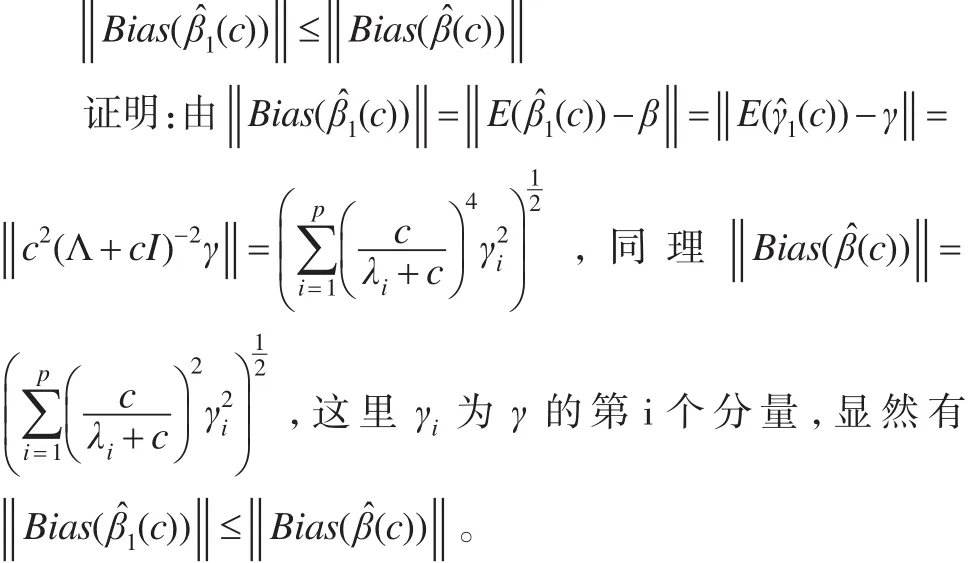
定理2：存在c*＞0，使得下面的式子成立：

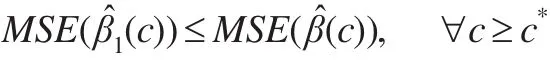
此估計方法中涉及的兩個參數：光滑參數h和嶺參數c。參數h的選取可采用交叉確認等方法確定，嶺參數c的選取應使下式達到最小，即：

3 模擬實驗

模擬如下半變系數模型：

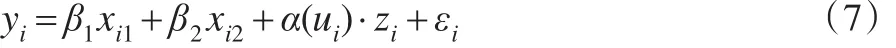
假定樣本數為n，協變量x1的觀測值x11，x21，…，xn1為從均勻分布U(-1，1)中獨立抽取的n個隨機數，變量x2與x1具有偏強復共線性性，條件數，不妨令xi2=2xi1+d，i=1，2，…，n(d的大小可以影響條件數k，一般地，d越小k越大)，協變量z的觀測值z1，z2，…，zn為從區間(-1，1)上的均勻分布U(-1，1)中獨立抽取的n個隨機數；u為區間[-1，1]上的n個等分點；ε1，ε2，…，εn為從正態分布N(0，σ2)中獨立抽取的n個隨機數。yi由公式（7）得到。對n組樣本數據 (yi，xi1，xi2，zi，ui)，i=1，2，…，n基于本文方法利用matlab編程，重復抽樣N=50次比較嶺估計和幾乎無偏嶺估計的優劣。

半變系數模型的實驗結果(兩種模型參數實驗，每種模型參數記錄3組實驗結果)如表1所示，變系數函數的擬合曲線見圖1，以及嶺參數c與均殘差平方和SSE的關系見下頁圖2。

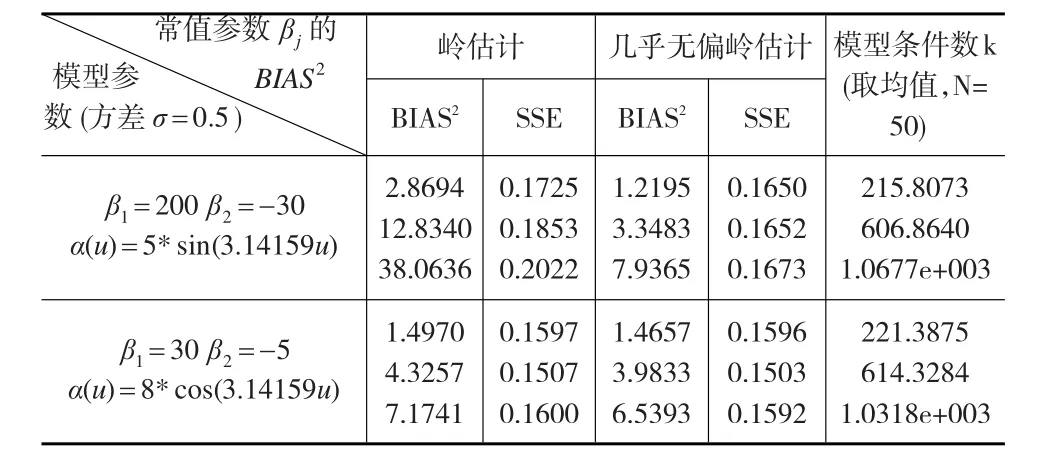
表1 不同估計的均偏差方(BIAS2)與均殘差平方和(SSE)的比較

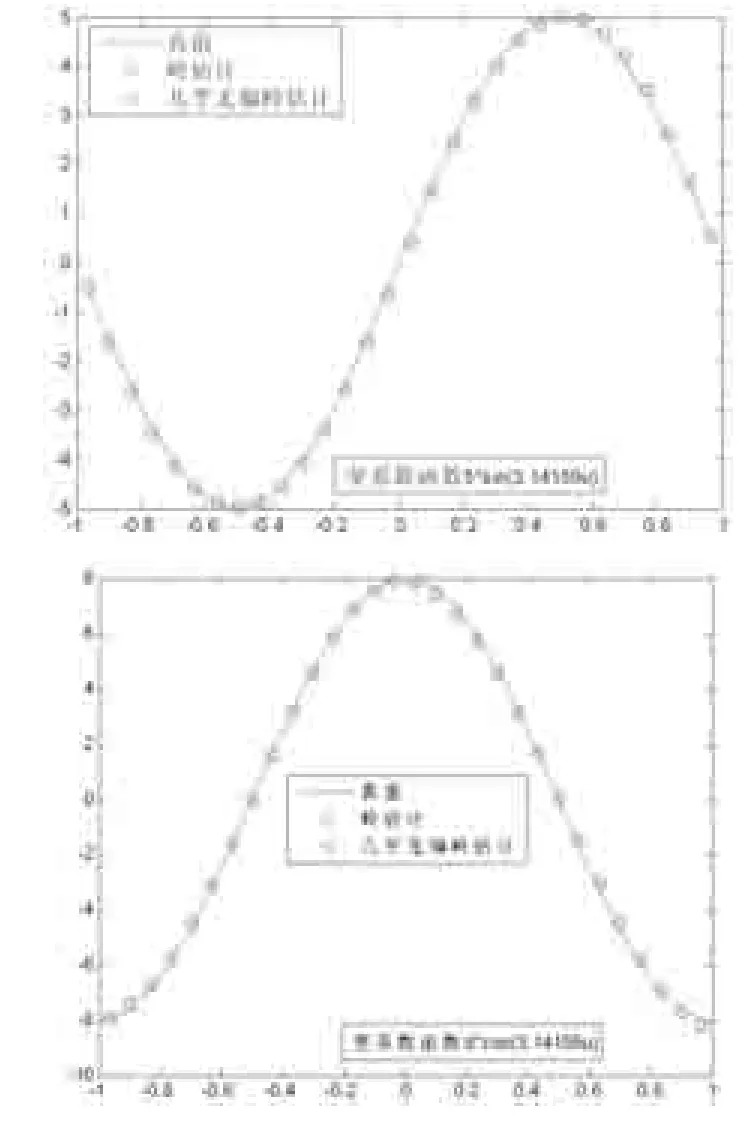
圖1模型中變系數函數在方差為0.5下的擬合圖

數值結果表明，在同一個模型參數下，幾乎無偏嶺估計的常值參數βj的BIAS2與模型的SSE均小于嶺估計的BIAS2與模型的SSE。圖1也表明了幾乎無偏嶺估計的變系數函數的估值最接近于真值，擬合程度更好。圖2表明光滑參數相同時條件數不同下，模型的幾乎無偏嶺估計殘差總是明顯小于嶺估計的殘差，且隨著嶺參數的增大而幾乎無偏嶺估計的殘差趨于穩定。

4 結束語

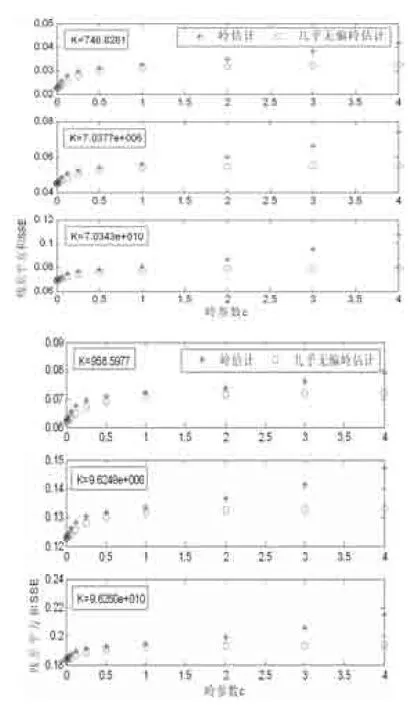
圖2兩種模型參數中嶺參數c與均殘差平方和SSE的關系(K為條件數)

本文針對半變系數模型存在的多重共線性問題，提出了幾乎無偏嶺估計。雖然本文得到的幾乎無偏嶺估計是有偏估計，但相比較嶺估計而言幾乎無偏嶺估計的偏要更小。模擬實驗的結果表明，在相同條件下，幾乎無偏嶺估計的常值參數βj的均偏差和模型的殘差都更小，變系數函數的擬合結果也優于嶺估計結果。