改進的兩階段最小二乘法在異方差模型中的應用

戴曉鳴 ，王維國

（1.東北財經大學 經濟學院，遼寧 大連 116025；2.大連交通大學 理學院，遼寧 大連 116028）

0 引言

在統計分析和計量經濟分析中，往往通過建立統計或經濟變量之間相互關系的模型，并通過一定的回歸方法對模型進行估計。一般而言，回歸模型需要做一定的假設，其中隨機誤差項的同方差就是其中一項重要前提假設。但是，在實際回歸分析過程中，隨機誤差項同方差的假定往往不能得到滿足，也就是說，回歸模型存在一定的異方差性。大多數的情況都不能充分滿足隨機誤差項同方差這個條件的，因此大多數的模型都存在一定的異方差性。這種異方差性的存在，是多種原因共同作用而引起的，其中，模型變量選取的偏誤、截面數據各單位偏差較大等因素是造成回歸模型異方差的主要原因。如果在變量選取中出現重要變量疏漏，那么該變量便歸入模型的隨機誤差項中，結果便造成了異方差。而截面數據中，各個單位之間的偏差可能較大，從而內生性地造成模型的異方差。異方差模型下，普通的OLS方法進行估計得到的結果具有明顯的有偏性，這與無偏性的假設相悖，因而OLS方法已不適用。當然，目前學術界已采用多種方法檢驗、修正或應用于異方差模型。本文嘗試提出基于正交表的方法的一種新的兩階段最小二乘法，并比較它與傳統兩階段最小二乘法在異方差模型的應用。

1 傳統兩階段最小二乘法對異方差模型估計

多元回歸模型中，假定 (x1i，x2i，…，xpi，yi) ，(i=1，2，3，…，n)為兩組樣本收據。首先，要利用多元線性回歸的方法，將上述模型變為一元線性回歸模型。然后，對每一個線性回歸模型進行異方差檢驗。為了具體分析模型的模型的有限性，下面引入一個自變量xi，對模型進行異方差檢驗。步驟1：將樣本數據按照自變量的x1按照數據大小順序進行排列，其他自變量與對應變量的相對關系保持不變。步驟2：將樣本分為N組，第i組有ni個元素，則n滿

步驟3：令x1i為i組的第一個自變量的組中值，x2ij為i組 的 第 二 個 變 量 ，以 此 類 推 ，滿 足 定 (x1i，x2ij，…，xpij，yij) ，(i=1，2，3，…，n;j=1，2，3，…，ni)。

步驟4：假定分組數據滿足如下多元回歸模型：

其中，誤差項為εij，滿足。接著，對式（1）進行變換，等式兩端同時除以σi，可得：

則誤差項為εij/σi。

步驟6：進行第二階段估計，將估計量代入變換后的新模型，則新模型的OLS系數估計量為原模型的GLS系數估計。

2 改進兩階段估計法對異方差模型估計

當樣本數據較小時，通過分組產生的重復數據會導致信息失真，部分樣本信息丟失，是的回歸模型的精度不高。為了提高回歸模型的精度，消除重復數據的影響，借鑒前人的研究，采用正交表的方法來改進二階段估計法的第一階段。

假定樣本 (x1i，x2i，…，xpi，yi)，(i=1，2，3，…，m)，滿足如下回歸模型：

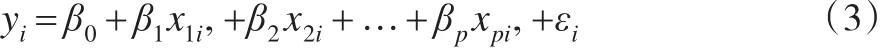
在模型（2）中，變量x1是引起異方差性的關鍵性變量。考慮到計算的簡化性與典型性，先假定p=3，利用正交表，產生重復設局L9(34)，然后對數據按照大小順序近分組，并進行兩階段估計。

步驟1：利用正交表獲取重復數據，Δ=0.01,第i個樣本數據通過變換后產生的數據如下：

步驟2：假定每一個因變量yi的觀測值滿足正態分布N(yi，θ2)，從正態分布中隨機產生9個數據，記作yij，其中i=1，2，…，m;j=1，2，…，9;θ2=0.01 ，且yij與 (x1ij，x2ij，x3ij)相對應。

步驟3：對i個樣本產生的觀測值按自變量從小到大排列，其他變量與自變量的對應關系保持不變，將與第i個樣本進行排序后的數據記作第i組，滿足i=1，2，…，m，該組的第一個自變量的組中值為x(1i)分組后的數據為(x(1i)，x(2ij)，x(3ij))。

步驟4：利用模型（3）對數據進行變化，兩邊同時除以σi，可得變換后的同方差模型：

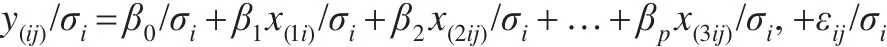
其中，εi/σi～N(0，σ2)。

步驟5：進行第一階段估計，由于：

這里的ni為正交表的試驗數，因此可采用第i組的方差估計第i個標準差的平方。

步驟6：進行第二階段估計，將估計量=代入變換后的新模型，則新模型的OLS系數估計量為原模型的GLS系數估計。

3 改進的兩階段最小二乘法估計異方差模型的數據模擬

通過簡單的數據模擬，對改進后的兩階段最小二乘法和傳統的兩階段最小二乘法分別進行估計和檢驗，并對結果進行比較，以判斷改進的兩階段最小二乘法在異方差模型應用中是否有效。

首先，假定簡單的回歸模型如下：

其中，i=1，2，3，…，n；隨機誤差項εi服從正態分布，且滿足不同樣本i下的隨機誤差項之間相互獨立。根據傳統的兩階段最小二乘估計方法，通過改變分組數k，便可能改變模型估計的誤差。這里，分別列出當取3、6和10時的回歸結果。為了使結果比較更加清晰，這里模擬時假定樣本容量較小，取n=30。其中，x1i、x2i、xpi,的數據序列由本文自行給定，但限于篇幅，此處略去具體數據。

本文給出均勻分布和正態分布兩種情況下的結果，具體模擬結果分別如表1、表2所示。其中MAEΣ、MAEy分別表示隨機誤差項的平均絕對誤差、被解釋變量觀測值的平均絕對誤差；R2為模型的可決系數；βi(i=0，1，2，3)為回歸系數。

表1 均勻分布條件下的兩種兩階段最小二乘法估計結果比較

表2 正態分布條件下的兩種兩階段最小二乘法估計結果比較

根據表1和表2的估計結果可知，不管是采用均勻分布類型還是正態分布類型，改進的兩階段最小二乘法估計的MAEΣ、MAEy和R2值都優于傳統兩階段最小二乘法，變量系數值βi也都比傳統兩階段最小二乘法得到的系數值精確。由表3和表4（見下頁）可以明顯地看出，運用改進的兩階段最小二乘法估計得到的系數，與既定系數之間的偏差率要明顯低于傳統兩階段最小二乘法的偏差率。例如，對于β2而言，運用改進的兩階段最小二乘法在均勻分布條件下估計得到的系數值，與既定系數的偏差率僅為-0.77%，而用傳統兩階段最小二乘法估計得到的系數值，對于k=3、k=6和k=10時，與既定系數的偏差率分別達到了-11.03%、-7.59%和-5.34%。因此，通過以上數值模擬可以充分表明，運用改進后的兩階段最小二乘法對異方差模型進行估計，得到的結果相對更加接近既定的模型參數，估計效果要優于傳統的兩階段最小二乘法。

表3均勻分布條件下不同方法估計系數結果與既定系數的偏差率（單位：%）

表4正態分布條件下不同方法估計系數結果與既定系數的偏差率（單位：%）

雖然通過適當控制分組數k，可以適當降低傳統兩階段最小二乘法估計異方差模型得到的誤差，提高精確度，但是這比想象之中要復雜得多。從表3的偏差率可以看出，當k取值為6時，四個參數的偏差率都要小于其他兩種取值（k=3和k=10）。但是，從表4偏差率又可以發現，在k取值分別為3、6、10時，四個參數的偏差率各有千秋，并不能指明到底k取值為何值時精度相對最高。在這種情況下，可能需要對k的取值進一步斟酌。在實際運用于異方差模型的過程中，這樣的情況難免會對模型處理帶來困難。但慶幸的是，運用改進的兩階段最小二乘法，在一定程度上可以解決這一問題。至少對于本例而言，無論是均勻分布條件還是正態分布條件，運用改進后的兩階段最小二乘法都能獲得相對理想的估計結果。

4 改進兩階段最小二乘法估計異方差模型運用的實例

為了進一步從經驗上證明改進的兩階段最小二乘法在運用于異方差模型時，相比傳統兩階段最小二乘法更具優越性，下面本文通過一則與我國經濟運行直接相關的案例進行分析。這里重點考察我國城鎮居民人均服務性消費支出與收入水平、地區宏觀經濟發展水平、服務業發展水平之間的關系。因變量Y代表城鎮居民人均服務性消費支出；自變量X1代表城鎮居民人均可支配收入、X2代表地區生產總值（GDP）、X3代表第三產業增加值。

采用2015年我國31個省、市、自治區的橫截面數據作為樣本。首先，通過普通的OLS估計，結果如下：

yi=-0.2103+0.2861x1i，+0.1927x2i+ …+0.6383xpi，+εI（9）

其中，可決系數R2僅為0.5278，F值也僅為3.6593，通過Goldfeld-Quandt檢驗法和帕克檢驗法都顯示了上述回歸模型存在異方差。

下面，利用上述改進的二階段估計模型，對這些變量進行分析。由于分組數據每組的樣本數據是一定的，為了避免每個樣本個數大，保證樣本數據的有限性，對傳統的二階段估計法進行改進。改進后的二階段估計不僅避免了樣本個數較大的缺陷，也增強了精度。為了突出改進方法的優越性，對比原方法與改進方法的參數估計差別，分別計算因變量Y的平均絕對誤差MAEy與系數R2，具體結果見表5所示。

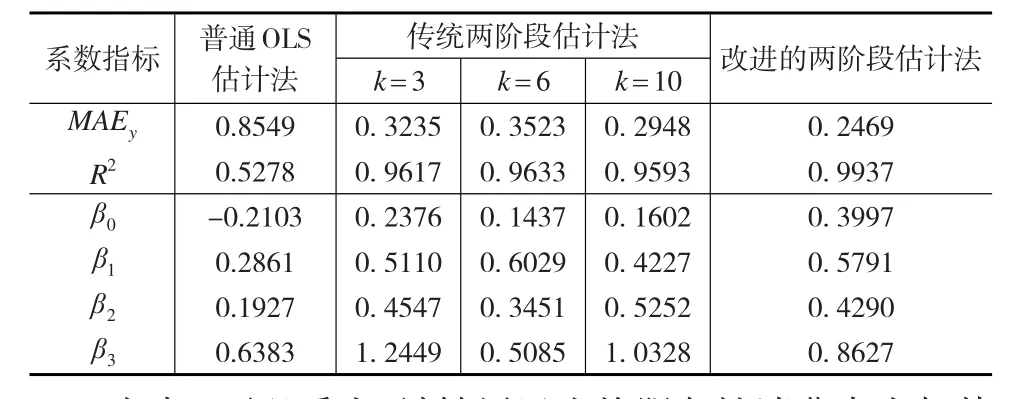
表5 普通OLS估計法、兩種兩階段最小二乘法估計法的結果比較

由表5可以看出，城鎮居民人均服務性消費支出與其可支配收入、地區生產總值、第三產業增加值都呈現明顯的正相關性。無論是改進的二階段參數估計，還是傳統的參數估計都的得出相一致的變化結果。具體來看，人均服務性消費支出與其可支配收入的估計系數為0.5791，說明當城鎮居民人均可支配收入每增加一個單位時，城鎮居民人均服務性消費支出將增加0.5791個單位。人均服務性消費支出與地區生產總值的估計系數為0.429，說明地區生產總值每增加一個單位時，城鎮居民人均服務性消費支出將增加0.429個單位。人均服務性消費支出與第三產業增加值的估計系數為0.8627，說明第三產業增長值每增加一個單位時，城鎮居民人均服務性消費支出將增加0.8627個單位。改進后的系數與分組的數據基本一致，相對而言，改進的數據比分組的數據更為穩定，基本位于分組數據的變動范圍內。

從平均絕對誤差MAEy來看，改進的二階段估計模型的平均絕對誤差更小，說明擬合程度更優，說明改進的二階段模型更有利于因變量的值接近實際的觀測值。隨著分組數的增加，估計的精度也會隨之提升。從系數R2來看，改進的二階段估計模型的系數明顯提高，由原來的0.9617、0.9633與0.9593提升到0.9937。由此可知，改進的二階段估計模型能更好地解釋實際結果。

5 結論

本文設計了一種基于正交表的方法的改進兩階段最小二乘法，將其應用于異方差模型中。通過比較該方法與傳統兩階段最小二乘法在異方差模型的應用，發現這種新型方法具有更高的估計精度，也在一定程度上解決了傳統兩階段最小二乘法在估計截面數據模型模型時因分組所帶來的精度問題。因此，本文認為所提出的這種改進的兩階段最小二乘法在處理異方差模型方面具有較高的實用性。盡管如此，本文所采用的改進兩階段最小二乘法在應用于異方差模型時仍帶有局限性，因為基于正交表擴大數據樣本之后，也會產生新的變量隨機性，也可能對估計誤差帶來影響。所以，在以后的研究中，需要對此問題探索新的方法，并作出相應修正，以使估計方法更加可靠。