組合預(yù)測(cè)中變權(quán)與定權(quán)的應(yīng)用比較

張 鵬

（太原工業(yè)學(xué)院 理學(xué)系，太原 030008）

0 引言

同一預(yù)測(cè)問題，往往不局限于一種方法，如果簡(jiǎn)單地舍棄誤差大的選擇誤差小的通常會(huì)丟失一些有用的信息，相對(duì)科學(xué)的做法是綜合不同模型的優(yōu)點(diǎn)，進(jìn)行適當(dāng)?shù)慕M合，即所謂的組合預(yù)測(cè)方法。多數(shù)組合模型的基本思想是將各單一模型預(yù)測(cè)結(jié)果通過加權(quán)平均而得到組合預(yù)測(cè)結(jié)果，有線性加權(quán)和非線性加權(quán)。

王莎莎等[1]以最小誤差平方和最小為準(zhǔn)則，將ARIMA、混合時(shí)間序列和GM(1,1)模型通過線性組合，運(yùn)用二次規(guī)劃得出最優(yōu)權(quán)值；陳啟明[2]提出了基于灰色關(guān)聯(lián)度的權(quán)值確定方法，這些組合模型大多共性都是同一模型在組合中權(quán)值是固定的，不隨時(shí)間變化，即定權(quán)組合。

本文針對(duì)線性組合權(quán)值的確定方法，分別構(gòu)造定權(quán)函數(shù)和變權(quán)函數(shù)，建立基于ARIMA、GM、BP三種單一模型的線性定權(quán)組合模型和線性變權(quán)組合，并應(yīng)用于GDP預(yù)測(cè)，比較二者的優(yōu)劣，進(jìn)而來說明組合權(quán)值的時(shí)效性。

1 組合模型及權(quán)值的確定方法

記實(shí)際觀測(cè)序列為{yt}，t=1，...，N，對(duì)其優(yōu)選m種不同的單一預(yù)測(cè)模型，表示第i種單一模型在時(shí)刻t的擬合值，各種單一預(yù)測(cè)方法時(shí)刻t在組合模型中的權(quán)值記為那么通過組合建立的模型則為單一模型預(yù)測(cè)值的加權(quán)平均，本文討論的為基于線性加權(quán)，即模型表達(dá)式如下：

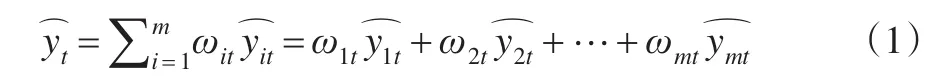
1.1 定權(quán)組合及權(quán)值確定法

所謂定權(quán)，即在組合模型中，同一單項(xiàng)模型在不同時(shí)刻權(quán)值是固定的，與樣本點(diǎn)的先后順序無關(guān)，可以理解為關(guān)于時(shí)間的常值函數(shù)，此時(shí)模型（1）為：

常見的定權(quán)確定方法有：誤差絕對(duì)值倒數(shù)法、誤差平方倒數(shù)法、二次規(guī)劃法等。本文采用的定權(quán)是誤差平方倒數(shù)法和二次非線性規(guī)劃法分別確定權(quán)值。

（1）誤差平方倒數(shù)法，這種方法根據(jù)單一模型的誤差來決定組合權(quán)數(shù)，誤差大則在組合模型中權(quán)值小。此時(shí)模型（2）中權(quán)值ωi為：

（2）二次非線性規(guī)劃法，該方法以誤差平方和最小為準(zhǔn)則，記為組合模型在t時(shí)刻的預(yù)測(cè)誤差；為第i種單一預(yù)測(cè)模型在t時(shí)刻的預(yù)測(cè)誤差，此時(shí)模型（2）中權(quán)值ωi由式（4）求得：

記誤差信息陣為E=(Eij)m，其中；權(quán)向量為；m維全 1列向量R=(1，...，，則式（4）可表示為：

根據(jù)真實(shí)值和預(yù)測(cè)值可得誤差信息陣E，基于Lagrange乘子法[3]，借助MATLAB中函數(shù)quadprod則可得式（5）的最優(yōu)解。

1.2 變權(quán)組合及權(quán)值確定法

所謂變權(quán)，與定權(quán)不同，即權(quán)系數(shù)隨時(shí)間變化而變化，此時(shí)組合模型為式（1）。在此，同樣以誤差倒數(shù)法和二次非線性規(guī)劃法來計(jì)算不同時(shí)刻的權(quán)值。

（2）二次非線性規(guī)劃法，t時(shí)刻的權(quán)向量ωt可由式（7）求得：

同樣根據(jù)求得的Et，基于Lagrange乘子法，利用MATLAB中函數(shù)quadprod可得式（7）的最優(yōu)解。

上述式（6）和式（7）最優(yōu)解給出了兩種樣本期內(nèi)的權(quán)值，在預(yù)測(cè)期，第i種單一模型在時(shí)刻N(yùn)+p時(shí)的權(quán)值，實(shí)質(zhì)為周期為N的移動(dòng)平均值[4]，定義為：

2 實(shí)證分析

由《中國(guó)統(tǒng)計(jì)年鑒》給出的年度GDP數(shù)據(jù)（1978—2015年），訓(xùn)練樣本數(shù)據(jù)為1978—2011年，測(cè)試樣本為2012—2016年，外推預(yù)測(cè)2017—2019年。首先進(jìn)行單一模型ARIMA、GM、BP的訓(xùn)練，其次依據(jù)本文中定權(quán)和變權(quán)函數(shù)分別構(gòu)建兩種組合模型，最后通過以相對(duì)誤差指標(biāo)來分析模型的優(yōu)劣。

2.1 單一模型

2.1.1 ARIMA模型

由圖1明顯看出GDP呈現(xiàn)指數(shù)趨勢(shì)，為非平穩(wěn)時(shí)序，故先對(duì)原序列進(jìn)行對(duì)數(shù)變換log(GDP)，然后以ADF檢驗(yàn)為準(zhǔn)則，判斷是否平穩(wěn)，經(jīng)過一階差分運(yùn)算得到平穩(wěn)序列Δ log(GDP)，見圖2，最后結(jié)合自相關(guān)圖和偏自相關(guān)圖，綜合比較模型的AIC、BIC準(zhǔn)則，確定了模型ARIMA(4,1,0)，表達(dá)式如下：

圖1 1978—2015年度GDP趨勢(shì)

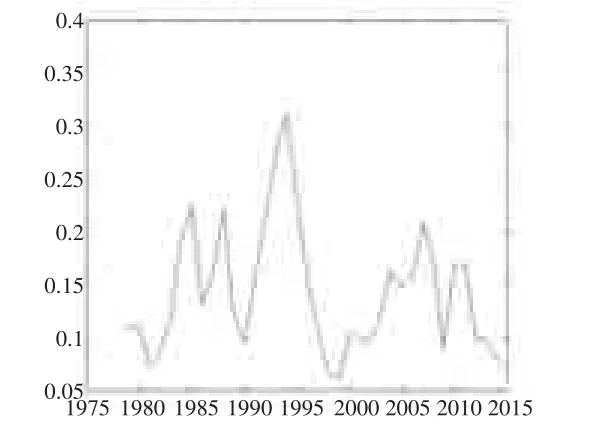
圖2對(duì)數(shù)GDP一階差分

模型參數(shù)均具有顯著性差異，且殘差為白噪聲，即不存在自相關(guān)性和異方差性，說明模型擬合結(jié)果較好。并用于檢測(cè)樣本的預(yù)測(cè)，預(yù)測(cè)值與誤差見下頁表1。

2.1.2 灰色GM(1,1)預(yù)測(cè)模型

在灰色GM(1,1)模型中，對(duì)原始數(shù)據(jù)首先進(jìn)行級(jí)比判斷，通過計(jì)算，原始數(shù)據(jù)的級(jí)比值均位于界區(qū)之內(nèi)，所以原始數(shù)據(jù)可用來建立灰色預(yù)測(cè)模型。

通過累減還原預(yù)測(cè)值公式:

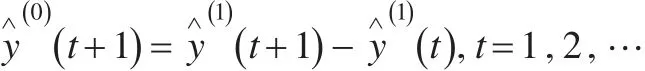
得到預(yù)測(cè)值及誤差，見表1。

表1 三種單一模型的預(yù)測(cè)值及相對(duì)誤差 （單位：億）

2.1.3 BP網(wǎng)絡(luò)預(yù)測(cè)模型

基于誤差反向傳播的多層前饋神經(jīng)網(wǎng)絡(luò)BP是應(yīng)用最廣的一種NN模型，其結(jié)構(gòu)的關(guān)鍵是隱含層節(jié)點(diǎn)數(shù)，本文采用“0.618法”來確定，其公式為：

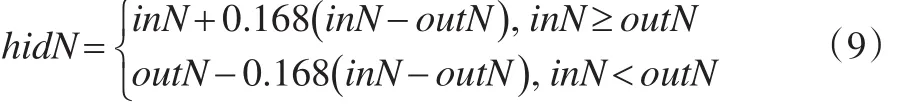
其中，hidN表示隱含節(jié)點(diǎn)數(shù)，inN表示輸入層節(jié)點(diǎn)數(shù)，outN表示輸出層節(jié)點(diǎn)數(shù)。本文首先將樣本數(shù)據(jù)利用極大極小法則歸一化處理至[0，1]區(qū)間，連續(xù)5個(gè)樣本作為輸入，即第6個(gè)數(shù)據(jù)作為輸出，即youtput=y(t)，由式（9）可知隱層節(jié)點(diǎn)數(shù)為6。預(yù)測(cè)結(jié)果見表1所示。

2.2 組合預(yù)測(cè)模型

2.2.1 定權(quán)線性組合

將ARIMA、GM、BP模型定權(quán)組合，通過式（3），得權(quán)值依次為：0.5410、0.1157和0.3433，得到相應(yīng)組合模型的預(yù)測(cè)值見表2；通過求解式（5）得到權(quán)值依次為：0.3214、0.2661和0.4125，得到相應(yīng)組合模型的預(yù)測(cè)值見表2所示。

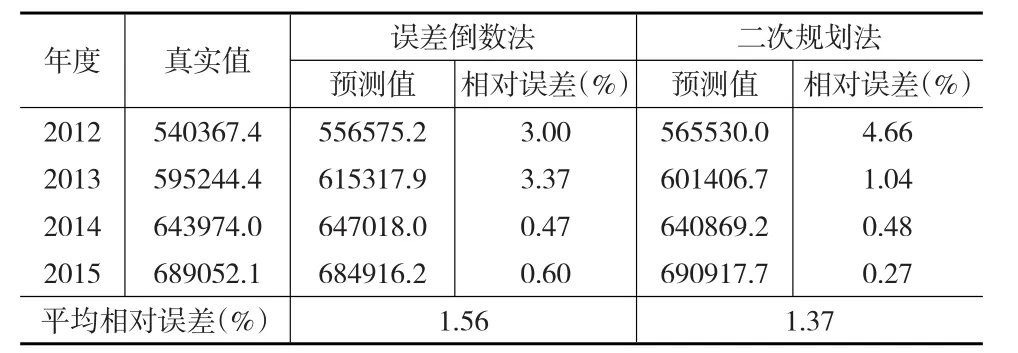
表2 定權(quán)組合模型預(yù)測(cè)對(duì)比

從表2可看出，定權(quán)組合下，相比誤差倒數(shù)法，二次非線性規(guī)劃確定的權(quán)值對(duì)檢測(cè)樣本的預(yù)測(cè)精度略高。相比表1，兩種組合的平均相對(duì)誤差均小于所有單一預(yù)測(cè)模型的平均相對(duì)誤差。

2.2.2 變權(quán)線性組合

將ARIMA、GM、BP模型進(jìn)行變權(quán)組合，通過式（6）和求解式（7），得訓(xùn)練樣本各時(shí)刻的權(quán)值，進(jìn)而通過計(jì)算式（8）得檢測(cè)樣本各時(shí)刻權(quán)值，見表3所示；最后得到相應(yīng)組合模型的預(yù)測(cè)值，見表4所示。

表3 變權(quán)組合下的權(quán)向量

表4 變權(quán)組合模型預(yù)測(cè)對(duì)比

綜合比較表2、表4，不管是誤差倒數(shù)法確定的權(quán)系數(shù)，還是二次非線性規(guī)劃法確定的權(quán)系數(shù)，變權(quán)組合得到的相對(duì)誤差均值小于定權(quán)得到的誤差；而且相比誤差倒數(shù)法，二次非線性規(guī)劃法確定的權(quán)系數(shù)在定權(quán)和變權(quán)組合中要優(yōu)。

基于二次非線性規(guī)劃變權(quán)組合模型，表5給出2016—2019年GDP的預(yù)測(cè)值。

表5 GDP預(yù)測(cè)值 （單位：億）

表5給出2016年的預(yù)測(cè)值為735218.6，而實(shí)際GDP為744127，預(yù)測(cè)結(jié)果的相對(duì)誤差為1.20%，進(jìn)一步說明變權(quán)重組合預(yù)測(cè)方法相對(duì)定權(quán)重組合預(yù)測(cè)方法具有較高的預(yù)測(cè)精度，即對(duì)于時(shí)間序列數(shù)據(jù)，組合預(yù)測(cè)的權(quán)值具有時(shí)效性。

3 結(jié)論

本文在以1978—2011年度GDP樣本數(shù)據(jù)，建立ARIMA，GM(1,1)以及BP的定權(quán)于變權(quán)組合預(yù)測(cè)模型，對(duì)2012—2015年數(shù)據(jù)進(jìn)行檢驗(yàn)，并進(jìn)一步預(yù)測(cè)未來短期的GDP發(fā)展趨勢(shì)，得出時(shí)間序列數(shù)據(jù)的組合預(yù)測(cè)權(quán)值具有時(shí)效性。相比單一模型和定權(quán)組合，變權(quán)組合具有一定的優(yōu)勢(shì)，但是受影響因素多的復(fù)雜性，接下來研究基于多因素變權(quán)非線性組合對(duì)時(shí)間序列預(yù)測(cè)的問題。