貴州省城市規模分布及異速生長特征
——基于分形理論的研究

， ，

(1.貴州師范大學 喀斯特生態文明研究中心， 貴州 貴陽 550001； 2.山東工商學院 工商管理學院， 山東 煙臺 264005)

城市體系規模分布的定量分析是城鎮化研究中的一項基礎性工作。城市規模分布就是城鎮人口在不同層級城市的分布，反映了地區城鎮化過程，而城市規模和分布結構則直接關系到城鎮體系功能的發揮和競爭力的提升。異速生長是城市地理學理論研究中一個非常重要的規律，有助于分析城市的時空演變和等級體系。運用分形理論探討國內平原地區城市體系的文獻已相當豐富，但對“人—地”關系矛盾突出、喀斯特石漠化問題較為嚴重的高原山區城市體系研究則較為鮮見。貴州是我國典型的喀斯特石漠化地區，造就了不同于其他地區的城市體系和發展過程。故本文選取貴州作為案例地，探討其城市規模分布規律及城市人口—城區面積的異速生長，這既是對分形理論應用的拓展，又可為貴州未來城鎮化路徑優化提供理論基礎和實踐參考。

一、學術背景與研究進展

一般來說，一個地區城市規模的大小，容易直接觀察得到，但對一定時期內城市規模的演變特征及其規模分布，則需要充分論證。20世紀以來，國內外學者從經濟學和城市地理學的視角對這一系列問題開展了深入研究，針對城市位序—規模有許多具有代表性的觀點。而城市規模效益最大化需要有合理的城鎮規模分布，因此，城市規模分布的相關研究就顯得非常重要。國外學者利用城市分形理論，主要研究城市個體的屬性，即其形態、結構、演化機制等問題。B.B.Mandelbrot較早直接運用分形理論來研究城市位序—規模法則的分維數性質〔1〕。M.Batty，A.S.Fortheringham等利用受限擴散凝聚模型(DLA)和電介質擊穿模型(DBM)模擬了英國Cardiff市和美國Taunton市的分形生長和空間擴散，開辟了城市模擬研究的新途徑〔2～3〕。R.White，G.Engelen利用圖式細胞自動機(CA)揭示了城市化過程中空間結構的分形演化及其混沌動力學〔4〕。Frankhouser對全世界主要城市的空間結構進行了分形研究，較為系統地探索了分形理論在城市規模分布中的實踐效果〔5〕。自20世紀90年代中期Batty，Frankhouser等分別出版有關“分形城市”研究的理論專著之后，國外的相關成果逐漸減少〔6〕。

在國外分形城市研究進入低潮之際，國內城市地理學分形理論研究崛起。陳彥光等討論了城市位序—規模問題的分形性質和退化形式，探討了Zipf定律的理論基礎〔7〕；隨后，又提出等級規模結構的分形維數及其地理意義〔8〕，并證明了城市體系二倍數規律與位序—規模法則的等價性〔9〕。以分形理論為基礎，有學者對地區城市體系規模的分形結構和分形特征、城市人口規模變化規律等進行了實證研究〔10～12〕。孫在宏等借助城市體系位序—規模法則和異速生長定律，對江蘇省城市規模分布的相關問題進行了探討〔13〕。李茂等提出并利用分布偏離度的概念，認為中國城市系統分布偏離度較高，位序—規模分布對中國的情況相對不適用〔14〕。戚偉等借鑒城市位序—規模理論，提出城市流動人口服從類似規律的假設，并對城市流動人口與城市人口位序規模分布進行耦合分析〔15〕。周曉艷等根據2000～2012年我國地級及以上城市的建成區面積數據，利用位序—規模法則及分形理論，對我國城市用地規模分布的變化趨勢及不同區域城市用地規模分布變化的差異性進行了研究〔16〕。

已有研究成果不僅印證了分形理論的邏輯科學性，而且還運用分形理論實證探究過區域城市體系規模分布、人口—面積異速生長、流動人口分布等，為研究區域城市體系規模結構及分布提供了有益借鑒。

二、研究方法及數據來源

(一)研究方法

分形理論的探討對象是自然界和社會活動中無序而又具有自相似性的復雜系統〔17〕。由于分形體系的局部與整體是相似的，分形體系內的局部在一定程度上是其整體的再現和縮影〔18〕。分形是大自然的優化結構，運用分形理論規劃城市體系的等級結構，可以優化區域城鎮化進程〔8〕。

1.城市規模分布法則

在一個城市體系中，城市與城市之間在功能上的相互依存傾向于導致整個等級體系內部人口規模與其位序之間的特定關系。這種關系就是位序—規模法則，該法則描述了一個國家或區域中的城市規模分布規律。假設一個區域內有若干城市的分布，由于城市與鄉鎮之間沒有明確的界限，設定一個人口尺度r來進行度量〔19〕。當人口尺度改變時，區域城鎮的數目N(r)也會相應改變，即當r由大變小，N(r)就由小變大。劉繼生等認為當滿足下列關系式時：

N(r)∝rD，

區域城鎮累積數與人口尺度成負冪律分布，城市規模分布具有分形特征〔20〕。該式為城市規模分布的Pareto公式，類比Hausdorff維數公式，D是分維。可以證明，它與Zipf公式等價〔21〕。Zipf公式為：

P(k)=P1k-q，

(1)

式中k表示城市位序(k=1,2,…,n；n為區域中的城市總數)；P(k)是位序為k的城市人口數；p1為區域最大城市的人口數；q=1/D為Zipf維數，具有分維意義。當q=D=1時，有P1/Pn=n，即最大城市與最小城市的人口數之比恰為整個城市體系的城鎮數目，Carroll稱此種形態為約束型位序—規模分布〔22〕。當q<1，即D>1時，P1/Pn1，即D<1時，城市規模分布較為分散，城市體系的人口分布差異較大，此時首位城市的壟斷性較強。

2.異速生長模型

異速生長，一般理解為“與整個機體的絕對尺寸的變化相關的比例的差異”〔23〕，異速生長定律用于測度生物體的局部與整體的幾何關系〔24〕。類比于生物現象，城市地理系統中也會存在這種關系。基于這一思想，Beckmann提出城市體系異速生長方程〔24〕。據Nordbeck的研究，異速生長并不限于刻畫系統局部與整體的關系，一個生長體的兩個相關變量也可以滿足異速生長方程〔25〕。這種觀念在后續的研究中得到推廣，如城—鄉人口關系、人口—面積關系、城市—城市相互作用關系等〔26〕。

因篇幅有限，本文省略異速生長方程的推導過程，該方程的一般形式為：

式中的標度指數αij隱含有維數意義，xi表示要素Pi的某種測度(i=1,2,…,n)，該式具有廣義的分形性質。若設xi=A表示城區面積，xj=P表示城區人口，將參數α、β分別用b、a表示，該式可以表示為：

A=apb。

(2)

式中的標度指數b具有維數性質，在早先經過Dutton、Lee等人的實證之后〔27～28〕，Batty， Longley對城市人口—城區面積的異速生長關系作了分形幾何學的解釋〔29〕。大量的實證觀測數據表明，b值處于2/3～1之間，平均值約為0.85〔26，28～29〕。異速生長關系可能會退化，退化實質就是分形結構的退化〔30〕，盡管異速生長的最初定義是冪指數形式，但現實的地理現象還可能退化為指數、對數形式，甚至完全退化為線性關系〔28,30〕。劉繼生等認為越接近線性關系，系統的結構越退化〔31〕。

(二)數據來源及說明

本文采用城市城區人口和城市建成區面積作為模型構建的基礎數據，數據來源于《中國城市建設統計年鑒(2002～2015年)》，選取貴州省13個城市(貴陽市、六盤水市、遵義市、安順市、銅仁市、畢節市、興義市、都勻市、凱里市、清鎮市、赤水市、仁懷市、福泉市)作為樣本。城區人口是在該區域生活、工作和活動的經常性群體，更能反映城市現實的人口規模。探究一個區域的城市規模，考量的主要對象是城區人口。因此，本文在探究貴州省城市規模分布中，并未選取市區人口或市區非農業人口作為基礎數據。建成區面積是指城市行政區內實際已成片開發建設、市政公用設施和公共設施基本具備的區域(《中國城市建設統計年鑒》指標解釋)，本文在探究貴州省人口—面積異速生長特征中采用該指標作為城市面積的基礎數據。

三、貴州省城鎮規模分布

(一)城市規模分布演化規律

據城市規模分布分形性質，城市規模分布一般滿足Zipf位序—規模法則。在數理推導中，冪函數關系可以轉換為對數線性關系。本文將式(1)兩邊進行對數轉化，利用SPSS 22.0對2002～2015年貴州省13個主要城市的人口規模和位序進行線性關系擬合，即將InPk、InK進行線性回歸(結果見圖1)。擬合結果顯示，2002～2015年模型擬合的決定系數R2的最小值為0.929，表明擬合度較好(見表1)；各年份模型擬合的Sig值均小于0.05，表明線性關系顯著。擬合結果還表明，Zipf指數q值均大于1，即D值均小于1，表明全省城市規模分布較為分散，城市體系的人口分布差異較大，首位城市——貴陽市的壟斷性較強，在全省城市體系中占據主導地位；但從q值的趨勢來看，q值總體逐年在減小，并不斷在向理想指數1靠攏，說明全省城市體系的人口分布在逐年趨于均勻化，中間位序的城市在不斷發展(見圖2)。

圖1 2002～2015年貴州省城市位序—規模雙對數坐標關系

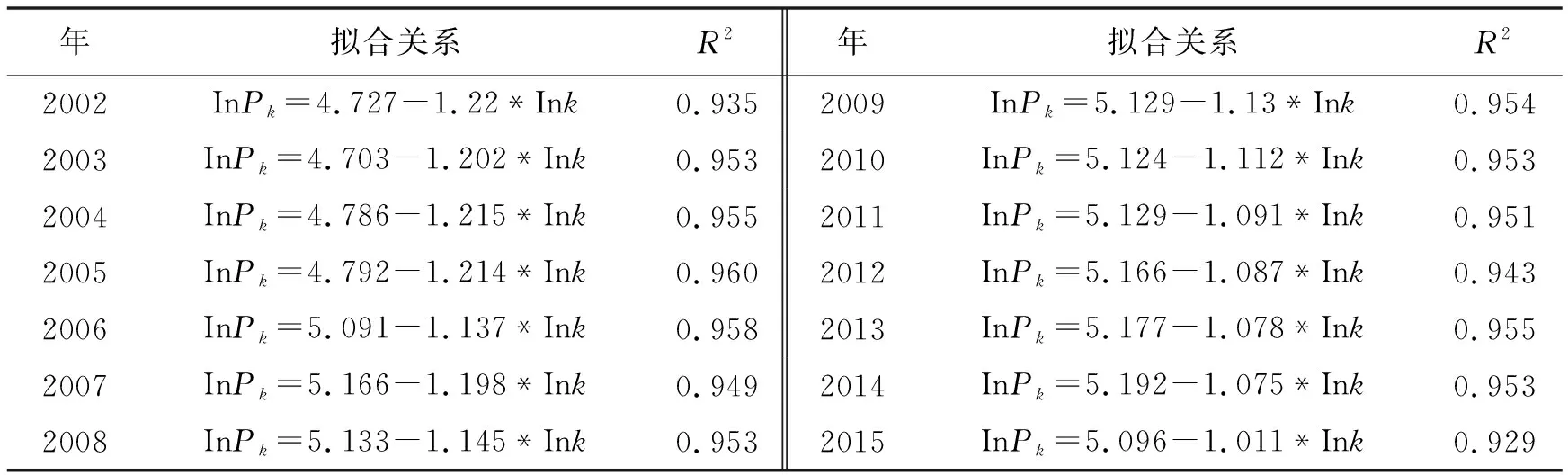
年擬合關系R2年擬合關系R22002InPk=4.727-1.22*Ink0.9352009InPk=5.129-1.13*Ink0.9542003InPk=4.703-1.202*Ink0.9532010InPk=5.124-1.112*Ink0.9532004InPk=4.786-1.215*Ink0.9552011InPk=5.129-1.091*Ink0.9512005InPk=4.792-1.214*Ink0.9602012InPk=5.166-1.087*Ink0.9432006InPk=5.091-1.137*Ink0.9582013InPk=5.177-1.078*Ink0.9552007InPk=5.166-1.198*Ink0.9492014InPk=5.192-1.075*Ink0.9532008InPk=5.133-1.145*Ink0.9532015InPk=5.096-1.011*Ink0.929

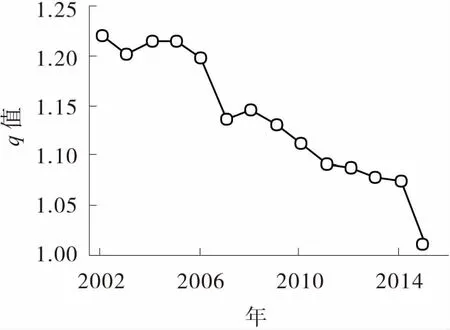
圖2 2002～2015年貴州省城市規模分布Zipf指數變化曲線

圖2反映了貴州省城市體系Zipf指數的變動軌跡。2002～2015年，q值增減起伏，除了在2004、2008兩年有小幅增長外，其余年份的q值均在減小，2002～2015年，q值下降17.13%。“十五”期間，q值維持在高位，減幅僅有0.49%，說明在“十五”期間，全省城市體系規模分布較為分散，城市體系的人口分布差異大，而且向理想值靠攏的速度非常緩慢；“十一五”“十二五”期間，q值向理想值1靠攏的速度比較快，說明在此期間全省城市體系規模分布在快速地均勻化，中間位序的城市在崛起，首位城市的壟斷性優勢在逐步減弱(見圖3)。“十五”期間是西部大開發的開局時期，政策性的影響力還處于“預熱”階段，貴州發達城市首先享受到政策紅利，此時城市規模分布的集中力量高于分散力量；“十一五”期間，西部大開發的戰略思路得到進一步明確和鞏固，公共服務均等化取得新成效，此時城市規模分布的分散力量較為明顯；“十二五”期間，尤其在《國務院關于進一步促進貴州經濟社會又好又快發展的若干意見》(簡稱“國務院2號文件”)出臺以后，全省走向“后發趕超”的高速發展期，城鎮化的戰略重要性進一步凸顯。貴州省人民政府提出全省高速公路三年建設會戰的戰略部署，使得全省的資源、資本和勞力逐漸向欠發達城市擴散，城市規模分布的分散力量高于集中力量，城市規模分布的Zipf指數越來越接近理想值，這反映出自然環境和社會環境共同作用于城市體系的演化〔32〕。

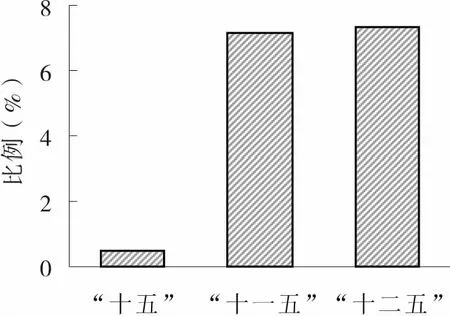
圖3 2002～2015年貴州省Zipf指數下降趨勢

(二)貴州省各城市人口規模演化規律

全省各城市人口規模的演化軌跡，呈現這樣一種現象：盡管貴陽市的首位壟斷性優勢一直處于高位，但中等位序和后位序的城市人口規模發展較快，且其人口規模位序處于不穩定狀態。

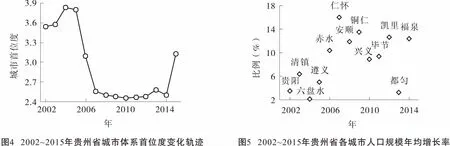
據城市首位度的概念及方法〔33〕，得到圖4所示的貴州省城市體系首位度2002～2015年間變化軌跡。2002～2015年，貴陽市首位度的最低值為2.46，按照馬歇爾(Marshall)對城市首位度的量化標準〔34〕，貴陽市在全省屬于“高度首位分布”。從長期來看，貴陽市的首位壟斷性不斷受到中等位序及后位序城市快速發展的挑戰，表現出城市首位度曲線下滑。

此外，貴陽市、遵義市、六盤水市初始城區人口規模較大的地區，在2002～2015年間人口規模年均增長率比較低；而除都勻市以外的其他中等位序及后位序的城市，人口規模年均增長率都比較高(見圖5)。這與圖2所示的貴州城市規模分布的Zipf指數在不斷變小、并逐年向理想值1靠攏的趨勢遙相呼應。

從表2和圖6所示的全省各城市人口規模位序的橫向對比分析來看，存在兩種現象：一是城市人口規模排名前兩位的貴陽市和遵義市，與排名后四位的清鎮市、赤水市、仁懷市和福泉市，它們的位序比較穩定，其位序的變異數均低于5%，有的甚至為0；二是中等位序的六盤水市、安順市、銅仁市、興義市、畢節市、凱里市、都勻市，位序波動比較大，其位序的變異數均在15%及以上。

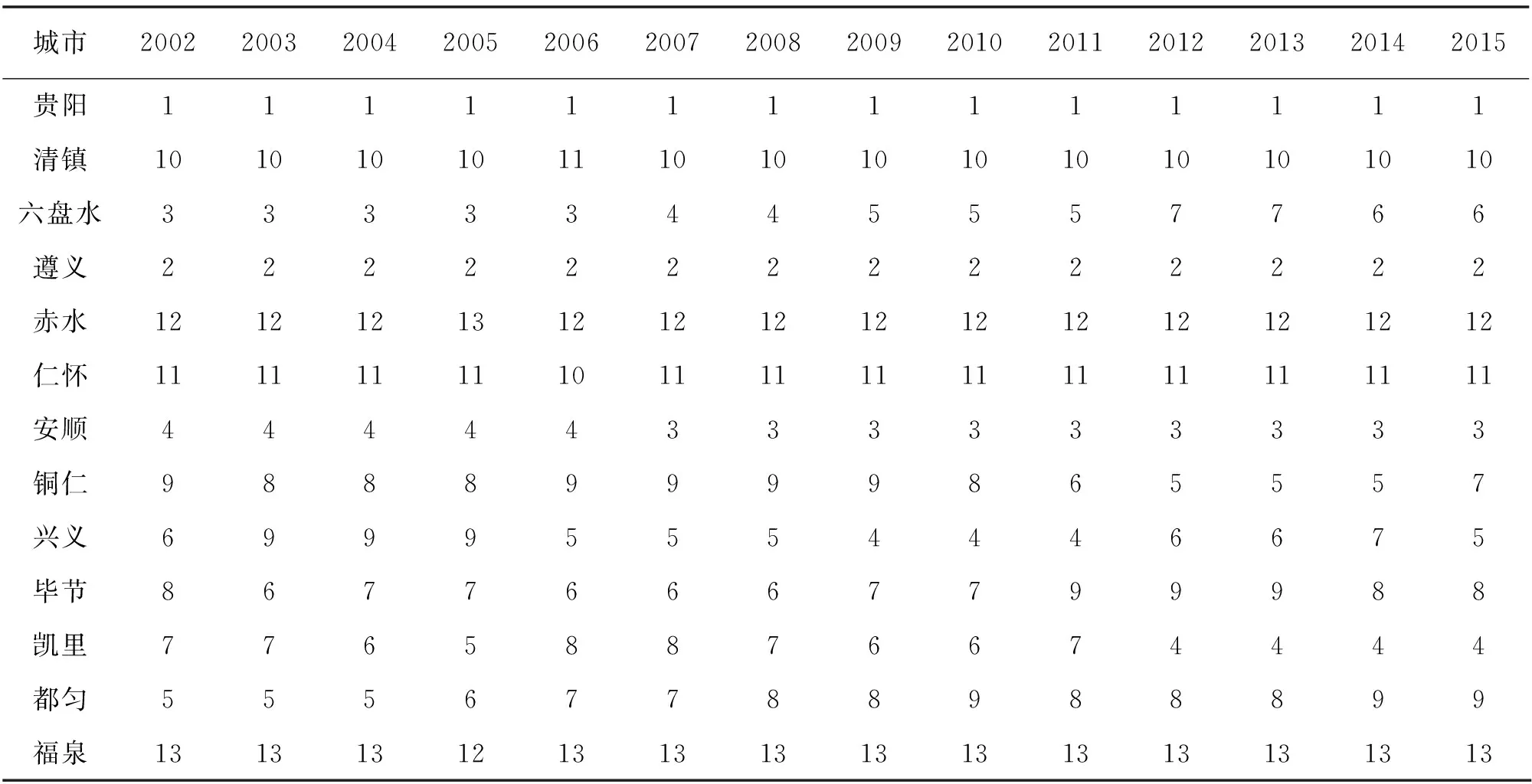
表2 2002～2015年貴州省各城市人口規模位序

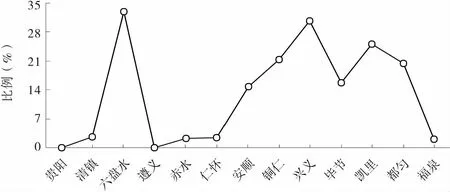
圖6 2002～2015年貴州省各城市人口規模位序變異系數對比

另外，貴陽市、遵義市在全省各城市中的壟斷性地位還未被撼動，而位序為后四位的城市盡管在2002～2015年間人口規模年均增長率較高，但皆非地級市，其規模發展受到地緣和行政的限制，難以扭轉位序靠后的局面。人口規模中等位序的城市整體波動幅度較大，參差不齊，有三種表現：一是城市人口規模增速較快，如銅仁市、凱里市、興義市，其城市規模位序在波動上升；二是城市人口規模發展緩慢，其位序下降，如六盤水市和都勻市；三是城市人口規模發展平穩，位序幾乎保持不變，如安順市、畢節市。這表明，在全省城鎮化的戰略推動下，中等位序的城市既迎來了發展機遇，但在經濟、社會和環境方面又避不開結構性調整的問題，在這些因素的綜合影響下，城市在發展的過程存在著一段“緩沖期”和“適應期”。

四、貴州省城市人口—面積異速生長特征

(一)全省人口—面積異速生長模型

城市用地形態已被證明具有分形結構，城市系統的異速生長與分形演化具有密切的梳理關系〔29〕，異速生長定律適用于描述城市人口—建成區面積的關系〔30〕。在異速生長的模型推導中，由于異速生長的原始定義表現為冪指數形式，而現實中的地理現象并非始終堅持服從冪指數規律，若冪函數的擬合優度小于其他曲線的擬合優度，則兩者的異速生長關系退化。表3和圖7顯示，全省城市人口—面積異速生長關系整體上已有退化的現象，直接表現為冪函數擬合優度整體小于線性擬合優度。

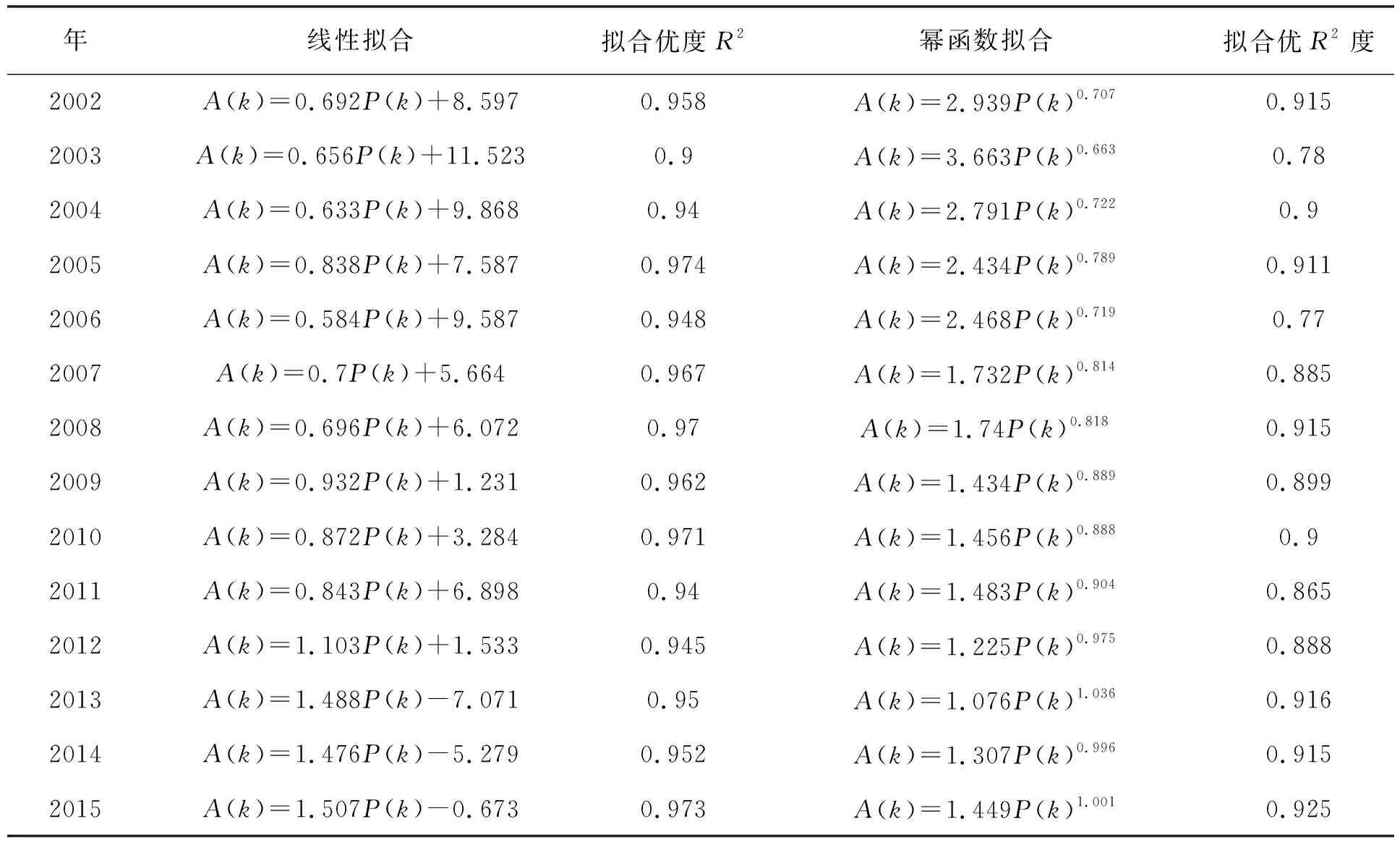
表3 2002～2015年貴州省人口—面積異速生長擬合模型

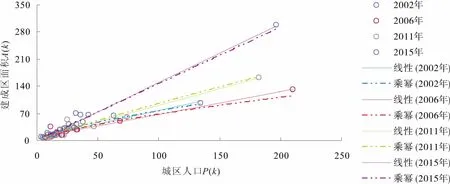
圖7 2002～2015年貴州省人口—面積異速生長線性和冪函數擬合關系

退化跡象表明全省城市體系整體性在減弱，這可能與全省城市體系尚未形成理想的規模序列結構、首位城市的強勢壟斷以及資源分配過于集中于少數城市等因素有關。另外，全省大多數城市的人口—面積異速生長關系表現出以指數函數擬合較高的半退化形式，并且除個別城市以外，其他城市的人口—面積異速生長模型擬合優度都不高(見表4)。這說明全省大多數城市的發展還存在一定的盲目性，人口規模與建成區面積之間的關系規律性不明顯，城市發展存在諸多不協調因素。

(二)貴州省城市體系人口—面積的異速生長關系分析

城市“人—地”的異速生長關系具有冪函數關系，可以用標度指數來解釋。如前所述，式(2)的標度指數b表示異速生長關系，具有維數性質。關于人口—面積異速生長關系的維數，學界存在爭議：有學者認為兩者之間具有二維的地理意義〔29〕；有學者認為，類比于生物發育的“表面—體積”約束，城市面積是二維變量，人口是三維變量〔27〕；還有學者認為，式(2)就已經隱含了三維空間的思想〔26〕。當b<1時，人口增長速度比城區面積增長速度快(文中稱為負異速)，城市向高層縱向發展，此時除了增加建筑物的密度以外，就是增加建筑物的高度；當標度指數b=1時，城市人口數量與城區面積同速變動，城市高度沒有變化；當b>1時，人口增長速度比城區面積增長速度慢(文中稱為正異速)，城市向扁平化橫向發展。

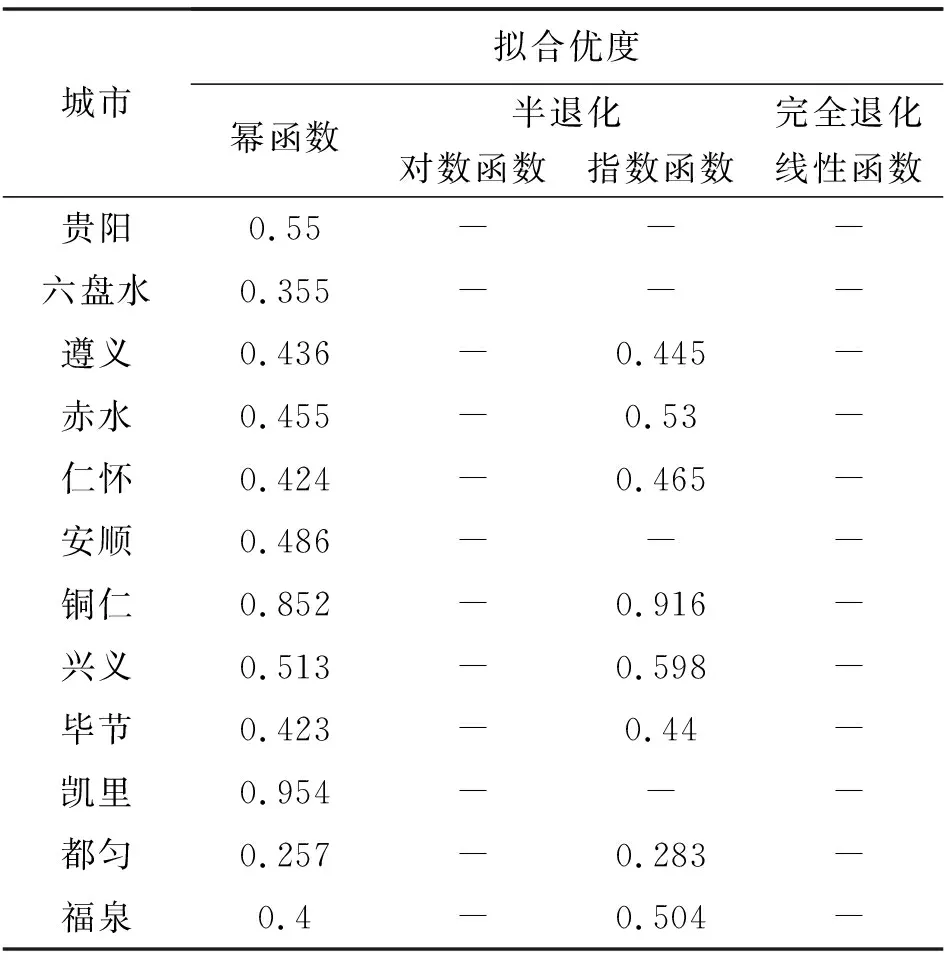
表4 貴州省各城市人口—面積異速生長模型擬合優度比較

人口—面積異速生長關系的維數之爭，不是本文的研究目的，因而不做詳細考究。就標度指數b的合理性而言，b<1符合發達城市的普遍法則〔13〕，即城市人口越多，在城市面積擴張受限的情況下，城市越向縱向的高層發展。

據表5，全省城市人口—面積異速生長的標度指數平均值為0.8515，與前文所述標度指數的經驗平均值0.85相當；且標度指數整體呈現逐漸增長的趨勢，兩者之間由負異速轉變為正異速，盡管在2014年該指數有所回落，但回落的幅度不大，仍然接近1。而擬合優度更高的線性擬合的系數同樣如此，只是由負異速轉為正異速的時間節點比冪函數擬合的標度指數早一年。由此可見，全省城市人口—面積之間正異速生長是城鎮化發展中的一個重要趨勢。即近年來，全省在城鎮化的過程中，城市面積的增長速度比人口要快，表現為城市面積在擴張，城市是扁平化的橫向發展。

表5 2002～2015年貴州省城市體系人口—面積異速生長系數及其關系演化

無論是冪函數擬合，還是線性擬合，全省城市人口—面積異速生長關系的轉折節點都在2012年(見表5)，這個時間節點不難解釋。2012年1月12日，針對貴州發展的國務院2號文件出臺。文件指出，貴州要“大力實施工業強省和城鎮化帶動戰略”。在城鎮化戰略的帶動下，貴州城鎮化表現為城市空間擴張為先，再產生集聚的城鎮。換言之，當前貴州城市人口—面積正異速生長關系是未來人口集聚的前提和基礎。由于貴州還處于城鎮化的建設期，人口—面積正異速生長關系維持在何種水平為合理，并將持續多久，還需要進一步的觀察和探討。

五、結論及討論

本文探討了貴州省城市體系規模分布及城市人口—面積異速生長特征，得到下述結論：

(1)貴州省城市規模分布較為分散，貴陽市在全省仍屬于高度首位分布，但從整體趨勢來看，中等位序及后位序的城市崛起速度較快，城市規模分布的集中力大于分散力，城市體系規模分布的Zipf指數逐年向理想值1靠攏。

(2)全省城市人口整體增長，但不同城市增幅有所不同，大城市和小城市的人口規模序列比較穩定，中等城市人口規模位序有增有減。從空間分布來看，貴陽、遵義、都勻、凱里、安順、畢節等黔中經濟區的城市是全省城市人口規模增長的中堅力量，貴陽市、遵義市的人口增長仍然是貴州人口城鎮化的主要拉力。

(3)全省城市體系人口—面積的異速生長整體上存在退化現象，城市體系整體性呈現減弱。此外，除銅仁市和凱里市以外，其他城市的人口—面積異速生長模型擬合優度不高，表明在城鎮化的過程中全省大多數城市人口規模增長與建成區面積之間具有“無律”性特征，兩者之間協調度較差，人力資源和地理空間資源未能得到有效開發；且全省人口—面積異速生長關系由負向正轉變，城市面積增長速度快于人口增長。

貴州省城市體系規模分布的Zipf指數q均大于1，即D均小于1，城市規模分布由分散向集中過渡，這與平原地區的浙江省和江蘇省Zipf指數q演化規律相反〔10,13〕。而不同類型地域空間的城市體系規模分布的演化方向是否相反，以及造成這種相反演化規律的原因，值得學術界進一步深入探討。本研究選取貴州省13個城市作為樣本，研究的空間尺度相對較大，未來可以縮小空間尺度，將范圍擴大至縣域城鎮，更能全面地摸清貴州省城鎮規模分布的規律和人口—面積異速生長的關系。