一種Ma0～4 TBCC進氣道氣動設計及性能分析

袁化成, 劉 君, 郭榮偉

(南京航空航天大學 能源與動力學院, 南京 210016)

0 引 言

在強調空天一體化的應用背景下，高超聲速飛行器已成為未來飛行器的主要發展方向之一，并受到世界各強國的高度重視[1-5]。高超聲速飛行器的飛行范圍十分寬廣，飛行高度0～30km，飛行馬赫數從亞聲速、超聲速一直延伸到高超聲速。動力裝置是實現高超聲速飛行的前提。吸氣式發動機可以從大氣中吸入氧氣，自身不需要攜帶氧化劑，減輕了飛行重量，大大提高了推進系統的比沖，從而成為高超聲速飛行器的首選動力裝置。然而，目前已有的航空渦輪發動機工作馬赫數一般為0～3，亞燃沖壓發動機工作馬赫數為2～5，超燃沖壓發動機工作馬赫數大于5。可見，任意一種單一的吸氣式發動機均不能獨立完成高超聲速飛行器的推進任務。因此，為了兼顧不同發動機的最佳工作速域并獲得最優的推進效率，將渦輪和亞燃/超燃沖壓發動機組合而成的推進系統，將成為高超聲速飛行器寬速域飛行的理想動力系統[6]。

TBCC推進系統依靠兩種不同工作模式的發動機完成從地面起飛、加速至超聲速飛行的過程，歷經亞聲速、跨聲速、超聲速直至Ma4以上。在此過程中，進氣系統對整個推進系統的性能起著關鍵作用，制約著整個推進系統功能的發揮和性能的提高[7]。在兩種不同工作模式的發動機的模態轉換過程中，進氣系統如何同時向渦輪通道和沖壓通道提供所需氣流，配合發動機完成動力模式轉換，且在此轉換過程中保持組合發動機的流量和推力平穩過渡等，都是決定TBCC發動機研制成敗的關鍵[8-10]。由此可見，TBCC進氣道不同于其他普通航空發動機的進氣道，它要在非常寬廣的飛行范圍內以及多變的飛行工況條件下，向TBCC推進系統提供高品質的流場。因此，進氣道需要實現幾何可變，以適應飛行狀態的變化。

本文在前期研究基礎上，開展渦輪基組合循環推進系統總體性能分析，確定發動機的推力及流量需求，從而約束進氣道的捕獲流量及捕獲面積。在此基礎上開展進氣道氣動型面設計及變幾何機構設計，并采用數值仿真方法進行進氣道氣動特性分析。

1 TBCC發動機總體氣動性能估算及分析

1.1 渦噴/沖壓發動機總體氣動性能計算模型簡介

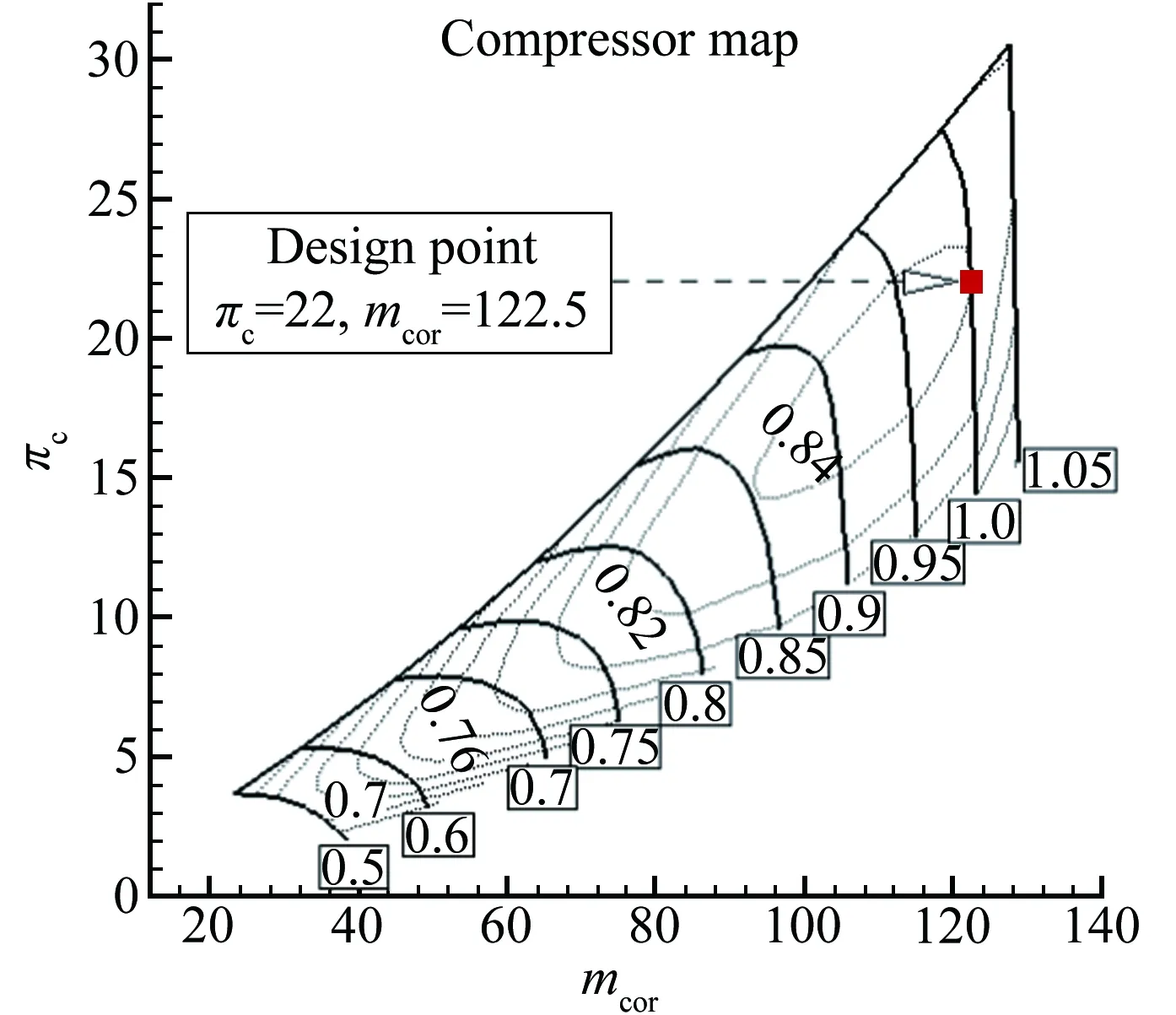
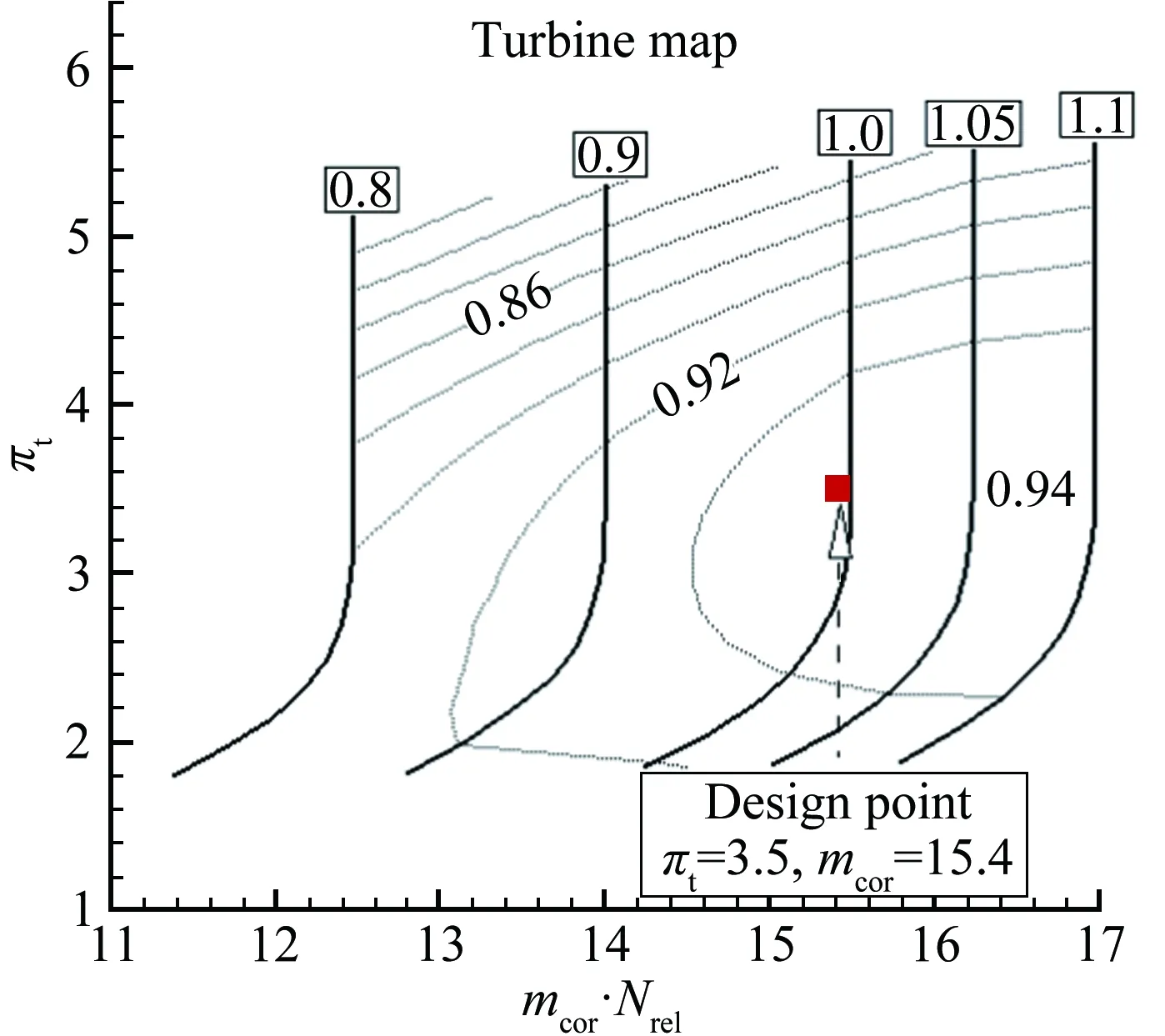
本文采用部件級建模方法對渦噴發動機進行性能計算，對已有特性圖進行縮放以獲得新發動機的特性圖，這種方法在初步階段的總體性能分析中是合理的。根據設計點參數對已有的壓氣機和渦輪特性圖進行縮放，縮放因子的計算方法與文獻[11]相同，縮放后的特性如圖1所示。圖中，橫坐標mcor、mcor·Nrel分別為折合流量以及折合流量與相對折合轉速的乘積，縱坐標πc、πt分別為壓氣機壓比和渦輪落壓比。

(a)

(b)

渦噴發動機模型中包含進氣道、壓氣機、主燃燒室、渦輪、加力燃燒室以及噴管。各部件的特性計算依據文獻[12]所述。在固定轉速的情況下，非設計點的計算需要猜測壓氣機壓比(πc=20)和渦輪落壓比(πt=3.0)，這兩個猜測值根據渦輪入口流量平衡方程(式(1))和壓氣機渦輪功平衡方程(式(2))進行修正。

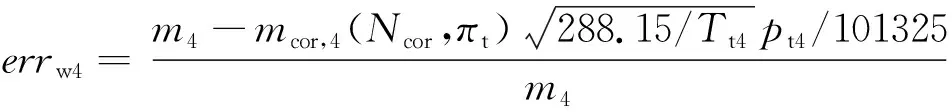
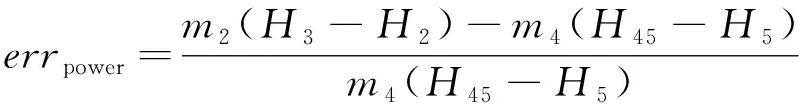
式中，errw4為渦輪入口截面流量誤差值，errpower為壓氣機和渦輪功誤差值；m2、m4、mcor，4分別為壓氣機入口流量、渦輪入口流量和渦輪入口折合流量；Ncor為折合轉速；Tt4、pt4分別為渦輪入口總溫和總壓；H為總焓，其下標2、3、4、45分別表示壓氣機入口、壓氣機出口、渦輪入口以及渦輪一級導葉出口截面。

本文采用流動推力函數進行沖壓發動機性能估算[13]。流動推力函數(Sa)表示單位質量流量的推力，該方法的主要優點是它能夠較為簡便地反映出流量、飛行馬赫數以及燃料添加等對沖壓發動機性能的影響。

考慮到壁面摩擦對壓縮部件的影響，本文將壓縮部件的增壓過程分為兩個部分：第一部分為斜激波系，該部分壁面摩擦忽略不計；第二部分是一個虛擬的與斜激波系出流平行的等壓通道，該通道內存在壁面摩擦但不存在激波，并且假設通道入口和出口截面的氣流是均勻的。總體性能參數發動機推力F以式(3)計算，耗油率SFC以式(4)計算。

(3)

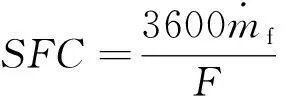
式中，m0、mf分別為發動機捕獲流量和燃油質量；Sa0、Sa9分別為遠前方及內噴管出口截面的流動推力函數值；T0、V0分別為遠前方來流溫度和速度；A0、A9分別為捕獲面積、內噴管出口面積；f為油氣比。

1.2 進氣道捕獲面積確定

根據渦噴發動機部件級模型，求得模態轉換結束點推力大小為70kN。假設沖壓發動機在Ma2.5時需求推力也為70kN，并假定加速度和升阻比(L/D)分別為0.1g和3.5，則可以求出飛行器的重量為18.5t。考慮到飛行器加速過程燃油消耗，飛行器的需求推力將發生變化。本文通過沖壓模態下燃油消耗量的計算，確定不同馬赫數下的需求推力。燃油消耗量以式(5)計算[14]。

·T(5a)

式中，TSFC為發動機的安裝耗油率，T為安裝推力，W為飛行器重量，Wf為燃油重量。本文將飛行任務按照0.5的馬赫數間隔進行劃分，從Ma2.5到Ma4.0分為3段，每一段加速度均保持0.1g。根據式(5)計算出沖壓模態下飛行器重量和需求推力的變化規律，如圖2所示。由圖可知：隨著馬赫數的增大，飛行器的重量從18.5t逐漸降低至16.3t，需求推力Freq從70kN逐漸降低至61.5kN。圖中的流量系數(φ)按照需求捕獲面積(A)除以進氣道捕獲面積(Ac)計算(進氣道捕獲面積按照1.0m2給定)。

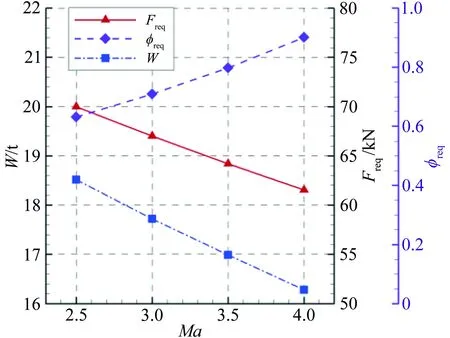
圖2 沖壓模態下的需求推力及飛行器重量

假設沖壓模態下燃燒室入口馬赫數保持在0.2附近，模態轉換過程燃燒室工作在化學恰當比Φ=1.0的情況，燃燒效率η=0.8，當來流馬赫數高于3.0時，燃燒室的化學恰當比降為0.71，此時燃燒效率為0.85。圖3給出了沖壓模態下，在滿足推力需求的前提下，燃燒室工作在不同化學恰當比時需要的流量(m)以及進氣道捕獲面積。從圖3可知：若沖壓發動機一直工作在化學恰當比為1.0的情況，則進氣道捕獲面積隨來流馬赫數從0.6m2增大至0.9m2；若沖壓發動機一直工作在化學恰當比為0.71的情況，則進氣道捕獲面積隨來流馬赫數從0.8m2增大至1.2m2。

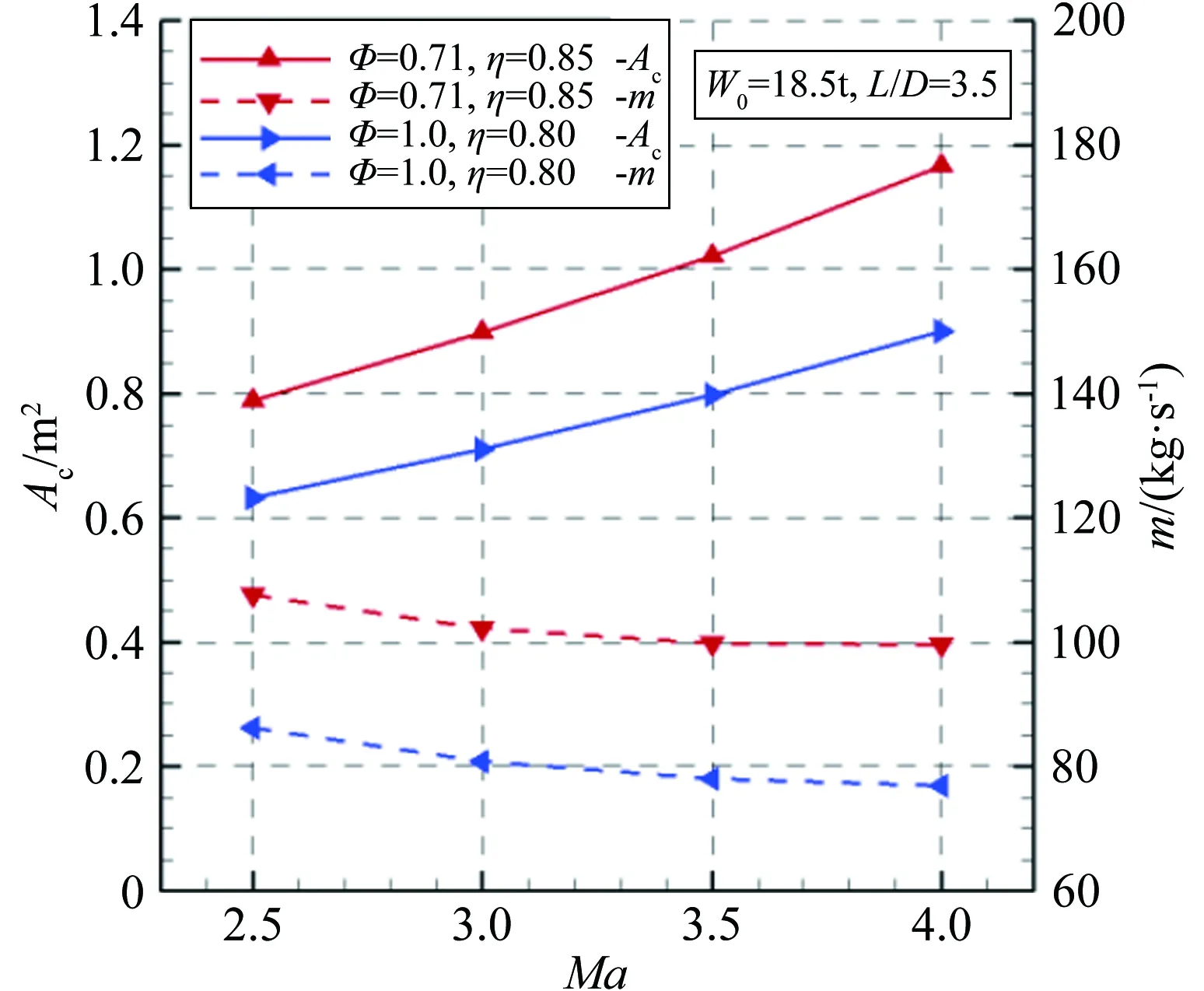
圖3 沖壓模態不同化學恰當比下的捕獲面積及流量

Fig.3Thecapturedareaandmassflowatdifferentstoichiometricratiooframjetmode

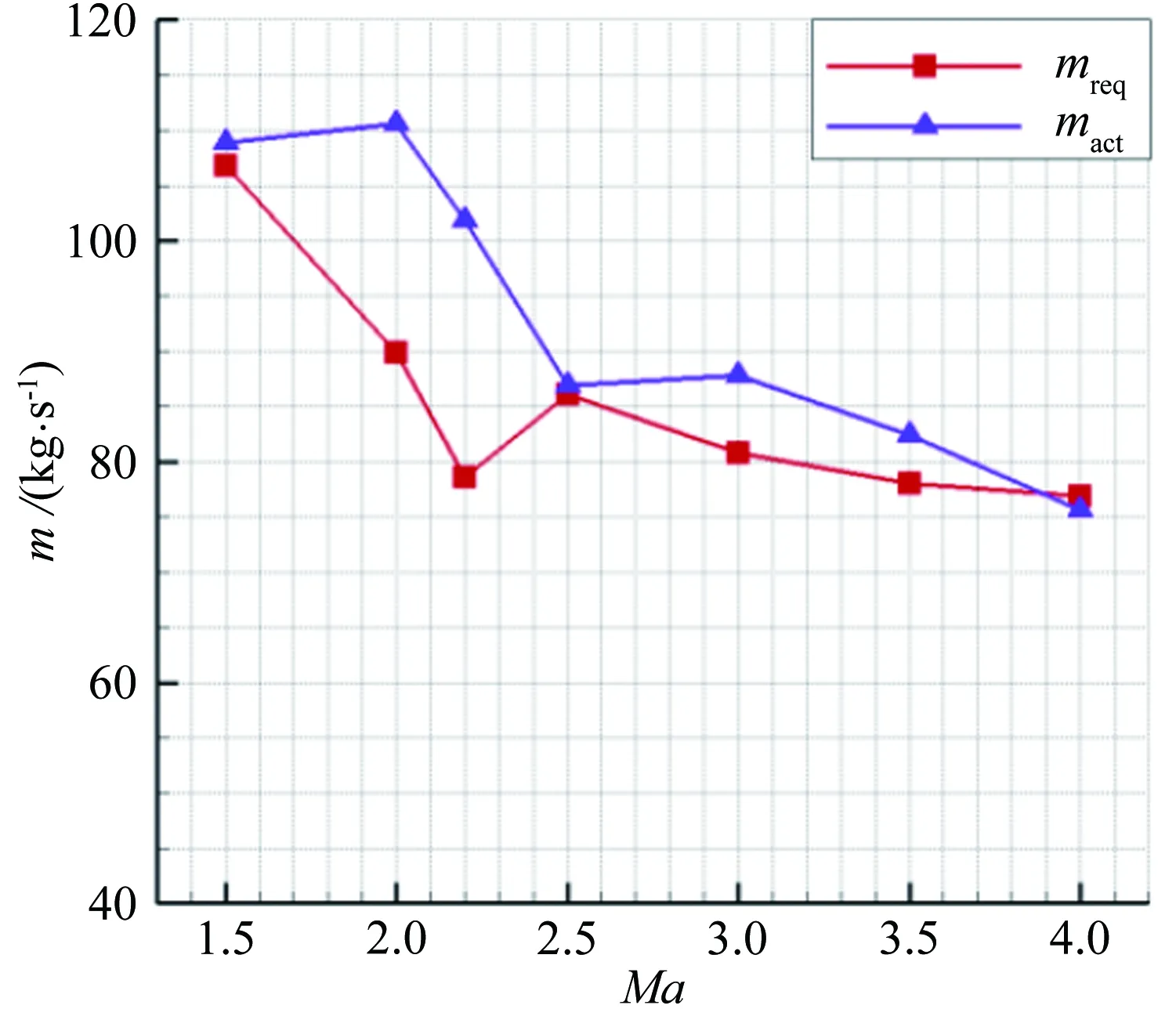
將上述發動機模型計算得到的需求流量(m)用于指導進氣道捕獲面積的選取。圖4給出了渦輪發動機沿飛行軌跡的需求流量，以及采用上述分析方法得到的沖壓發動機的需求流量，其中沖壓發動機的需求流量按照燃燒室化學恰當比為1.0時給定。同時給出了捕獲面積為0.8和1.0m2情況下進氣道的捕獲流量。從圖4可知：當飛行馬赫數大于3.0時，捕獲面積為0.8m2的進氣道所捕獲的流量不能滿足沖壓發動機的需求，而捕獲面積為1.0m2的進氣道能滿足流量需求，并有一定富余，便于模態轉換裝置的設計以及進氣道內流動控制。

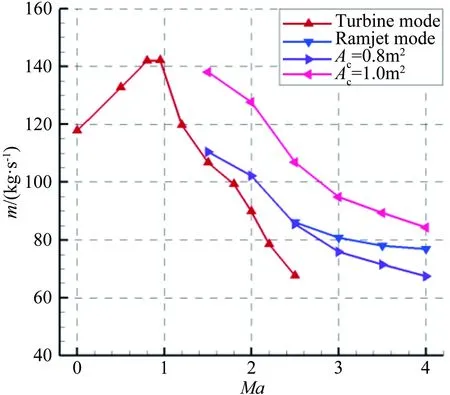
圖4 發動機需求流量與進氣道捕獲流量對比

Fig.4Thecomparisonbetweenmassflowrequiredbyengineandcapturedbyinlet

1.3 進氣道模態轉換點確定

采用上述驗證渦噴/加力渦噴發動機及沖壓發動機的計算程序，對組合循環發動機的特性進行計算，不考慮兩個流路的耦合效應。組合循環發動機的飛行軌跡按照來流動壓q=50kPa設計，如圖5所示。采用加力渦噴發動機將飛行器加速至模態轉換點后，沖壓發動機點火繼續為飛行器提供動力，直至達到設計馬赫數。

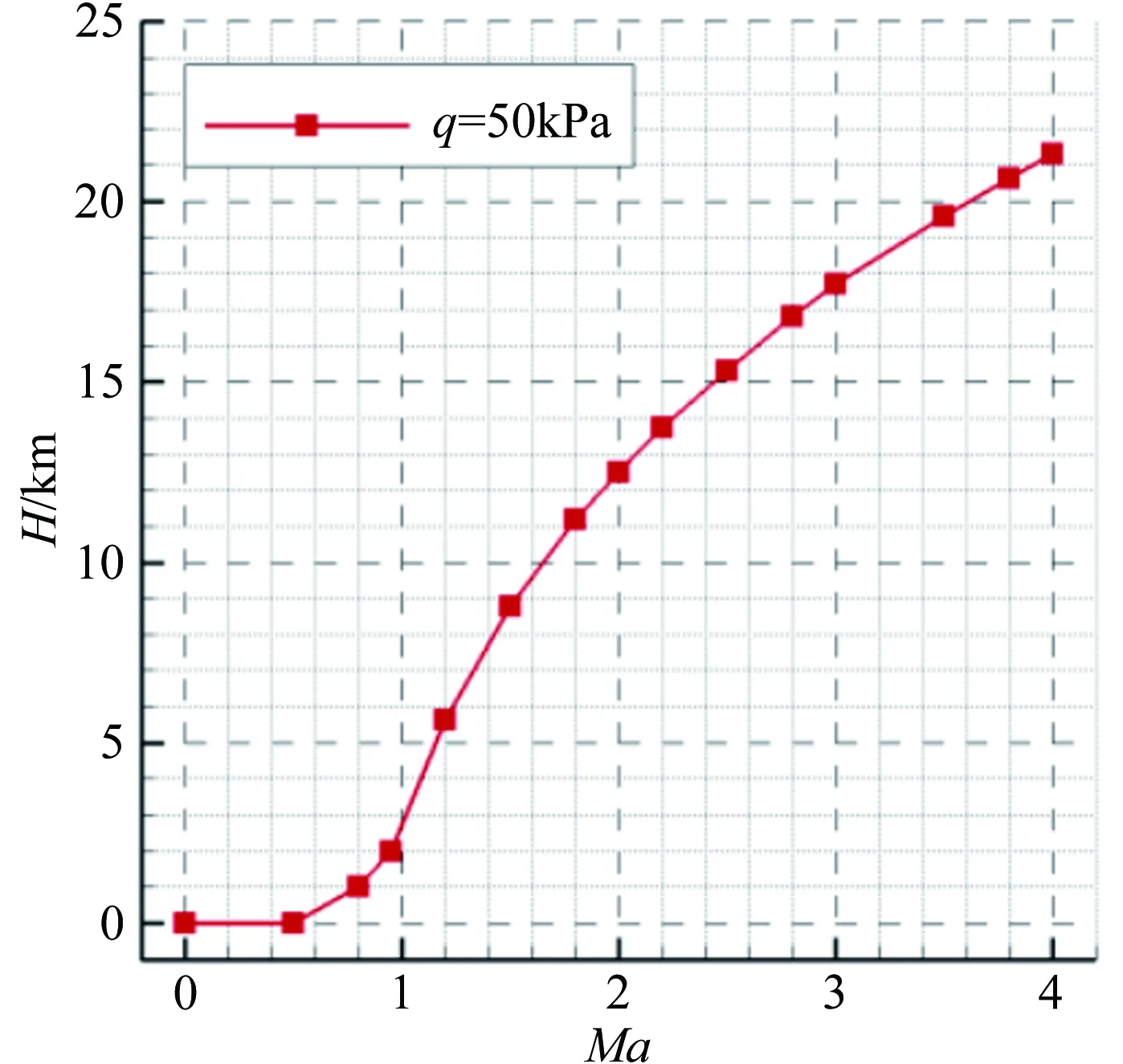
圖5 TBCC發動機飛行軌跡

根據以上給定的飛行軌跡進行計算，得到渦噴和沖壓發動機的推力及耗油率變化規律，如圖6所示。渦噴發動機的推力呈先增大后減小的趨勢，在Ma0.8以后，隨著馬赫數增大，進入發動機的流量逐漸降低，推力也逐漸降低。當飛行馬赫數為2.2時，渦噴發動機的推力已經小于沖壓發動機的推力，此后二者的差距進一步增大，因此，選擇Ma2.2為模態轉換起始點。

Fig.6ThethrustandSFCofTBCCpropulsionsystemalongtheflyingtrajectory

2 TBCC進氣道氣動方案設計及性能分析

2.1 TBCC進氣道型面及其變幾何機構設計

根據總體性能分析結果可知：TBCC進氣道的捕獲面積為1.0m2，模態轉換起始點為Ma2.2。進氣道捕獲寬度按照渦輪發動機入口直徑0.905m給定，因此進氣道捕獲高度為1.1m。TBCC進氣道型面如圖7(a)所示，壓縮面角度(δ)及喉道高度(H)等參數控制規律如圖7(b)、(c)所示。該進氣道采用兩級壓縮，第一級壓縮角δ1始終保持6.5°，第二級壓縮角δ2隨來流馬赫數的增大，從1.5°逐漸增大至11.5°。當來流馬赫數低于1.5時，進氣道為外壓式；當來流馬赫數高于2.0時，進氣道為混壓式。采用喉道前放氣的方式控制壓縮面上附面層厚度。喉道后通道分為渦輪通道和沖壓通道，通過模態轉換裝置的上下平動實現兩個流路的切換。

為了盡可能減少變幾何控制機構，將壓縮面2、3和4的變幾何過程采用一套控制機構實現，如圖8所示。將壓縮面2和3分別通過一根連桿與滑塊2相連，通過滑塊2的上下移動控制壓縮面2的角度變化，以及壓縮面3的位置變化。壓縮面3的運動受側壁滑軌以及滑塊2共同約束。壓縮面4通過鉸鏈2與壓縮面3相連，壓縮面3在運動過程中始終保持水平，當壓縮面3位置發生改變時，壓縮面4將繞鉸鏈3轉動。滑塊1和2之間組成雙滑塊機構，通過驅動滑塊1水平移動，實現滑塊2的上下移動，從而控制壓縮面的位置。

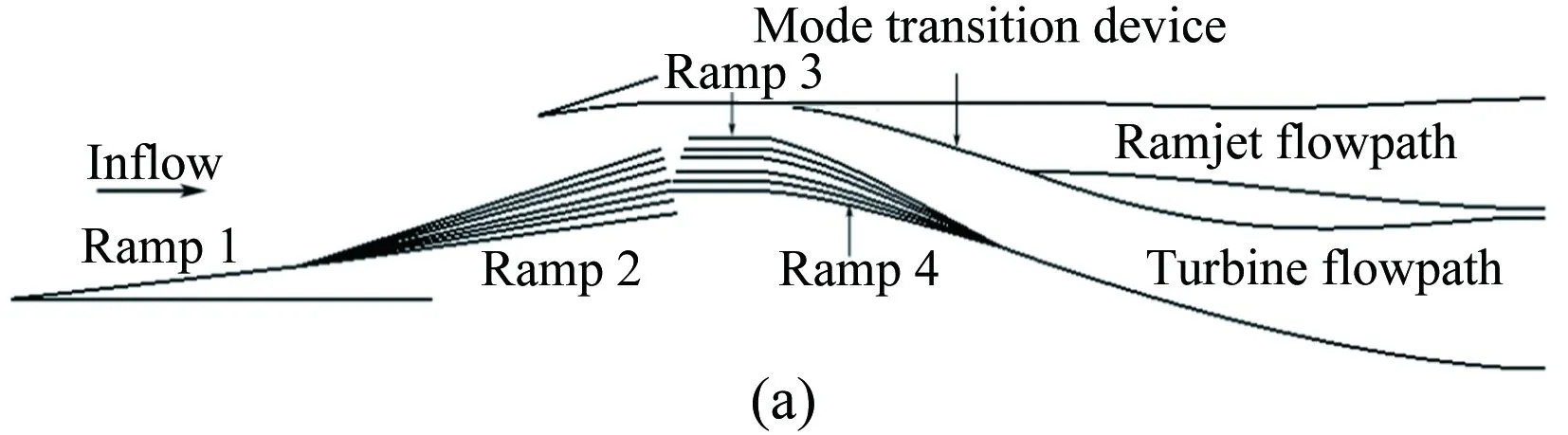
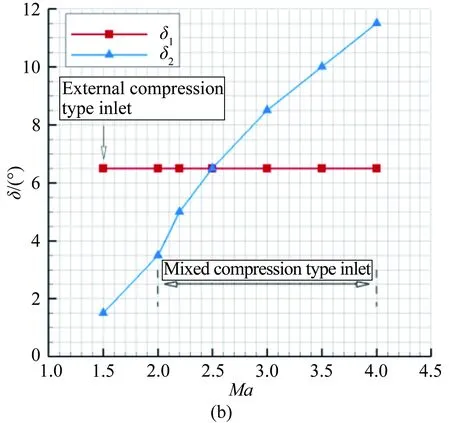
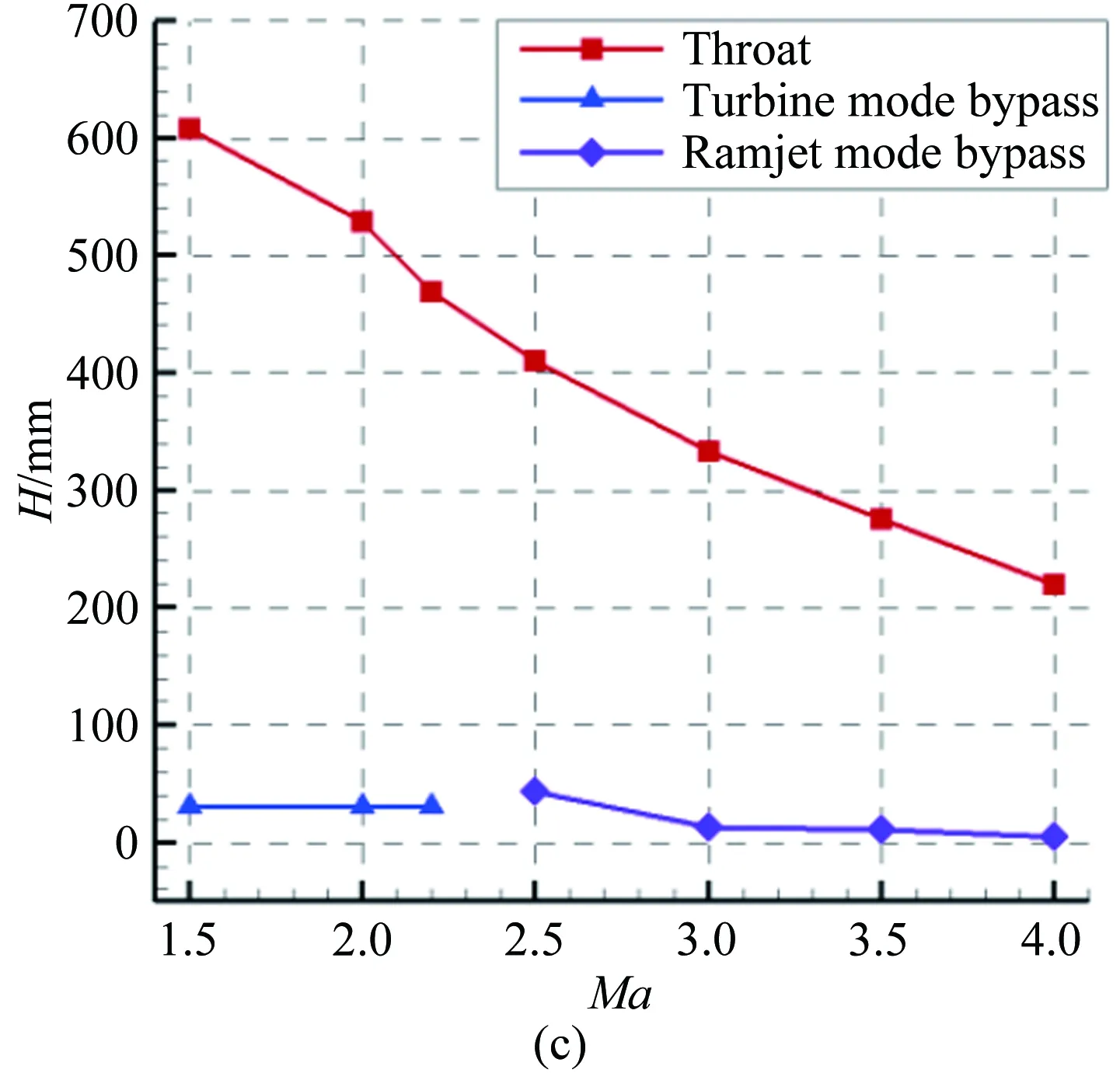
圖7 Ma0～4 TBCC變幾何進氣道型面及控制規律

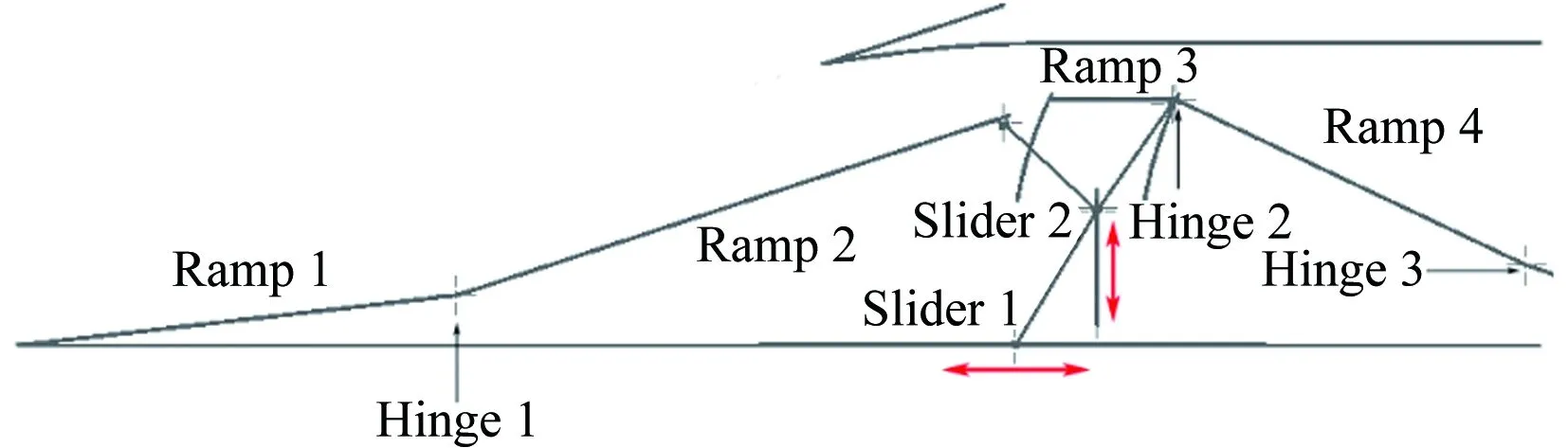
圖8 Ma0～4 TBCC變幾何進氣道機構簡圖

2.2 數值仿真方法

本文數值仿真分別使用有限體積法、基于MUSCL插值的Roe格式、二階中心差分格式對雷諾平均方程、無粘流通量、粘性通量進行離散，選取k-ωSST湍流模型，時間推進采用點隱式方法。對進氣道進行結構化網格劃分，總網格量約為160萬，壁面y+值保證在5以內，邊界條件為壓力遠場、壓力出口和絕熱壁面邊界，如圖9所示。氣體模型為理想氣體，以Sutherland公式計算氣體粘性。計算收斂以各方程殘差至少下降3個數量級為準，同時保證進氣

道出口流量等參數穩定。文獻[15]顯示該數值仿真方法可較為準確地模擬此類進氣道的流動，包括捕捉進氣道外壓激波及內通道結尾激波位置。

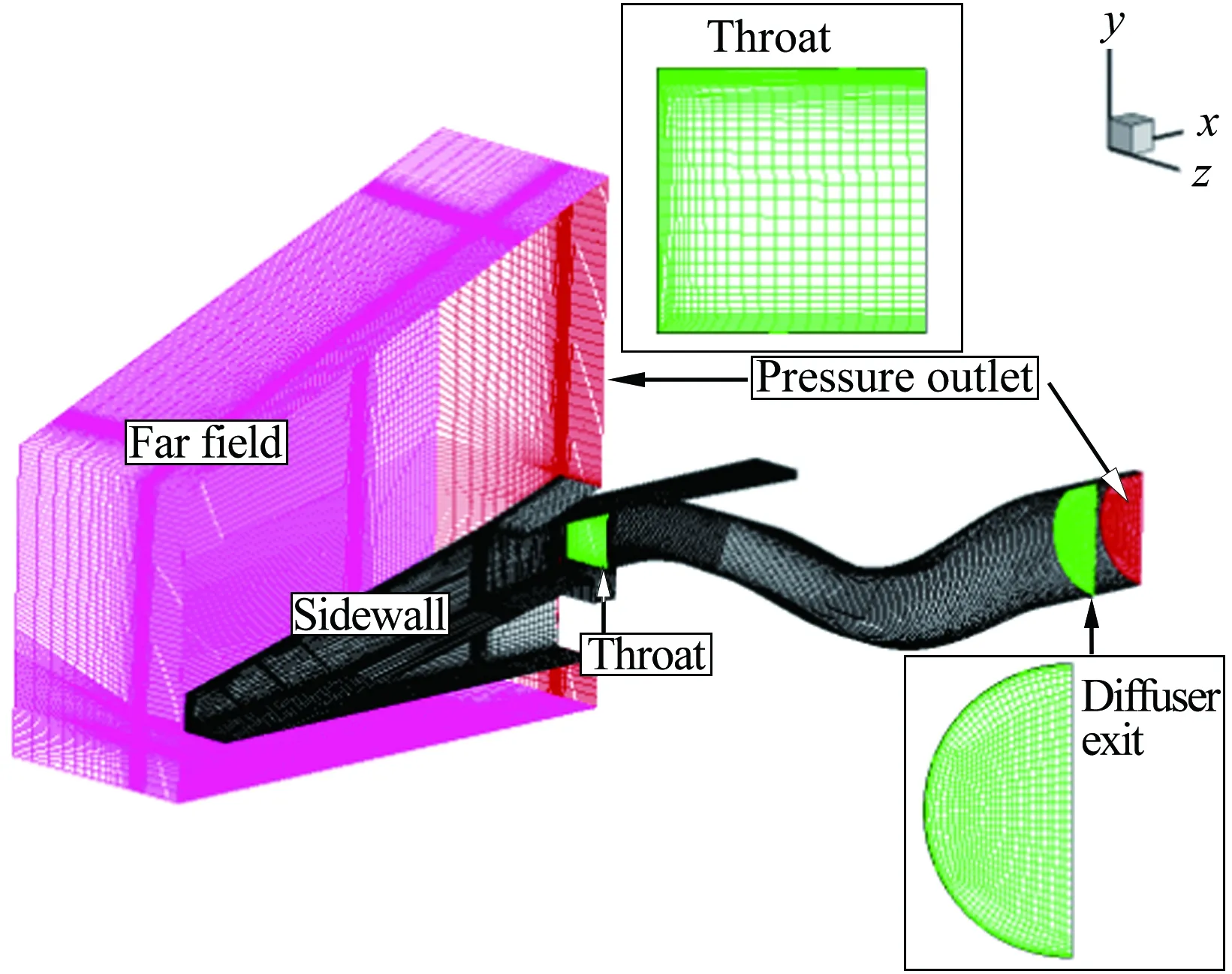
圖9 TBCC進氣道網格及邊界條件

2.3 TBCC進氣道渦噴發動機方轉圓擴壓段氣動設計及性能分析

在相同的進氣道外壓段和喉道段幾何尺寸下，對從模態轉換裝置后端至渦輪發動機進口段的方轉圓段開展氣動方案設計研究。在研究過程中，考慮了方轉圓段幾何長度、中心點控制參數、中心線以及沿程面積變化規律等典型幾何設計參數對渦輪流道進氣道氣動性能的影響。下面分別進行介紹。

2.3.1方轉圓擴壓段長度對進氣道氣動性能的影響

不同長度方轉圓段氣動型面設計過程中，僅改變擴壓段的幾何長度，其余典型設計參數(如中心線、沿程面積變化規律、偏距等)均保持不變。

圖10給出了渦輪流道進氣道出口性能參數隨方轉圓擴壓段幾何長度的變化曲線。其中，橫坐標表示方轉圓擴壓段幾何長度(Ld)，縱坐標表示渦輪流道進氣道出口馬赫數(Mae)、總壓恢復系數(σ)以及進氣道出口周向畸變指數(DC60)。從圖10可見：就本文研究的組合動力進氣道而言，Ld對Mae和σ影響較小，隨著Ld的增大，Mae和σ基本保持不變(Mae保持在0.4～0.45之間，σ在0.8附近)。DC60呈現先減小后增大的變化趨勢，約在3000mm位置處，畸變達到最小值0.65。

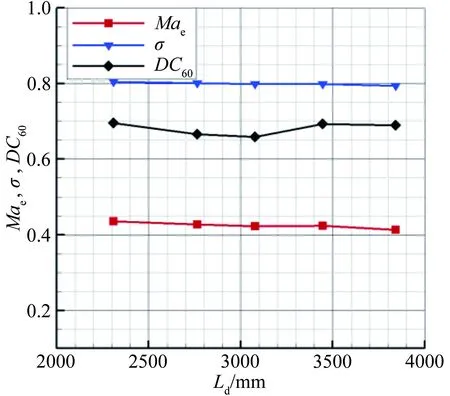
圖10 渦輪流道進氣道出口性能隨擴壓段長度的變化曲線

2.3.2方轉圓段中心控制點位置對進氣道氣動性能的影響

依據前文研究結果，選取方轉圓擴壓段幾何長度為3.0m，研究方轉圓段中心控制點不同縱坐標值ym對進氣道氣動性能的影響。ym變化范圍為0.6～2.0。圖11給出了不同ym值下的方轉圓段幾何造型。從圖中可見，隨著ym值的增大，控制點的偏距逐漸增大，方轉圓擴壓段的彎曲程度發生改變。

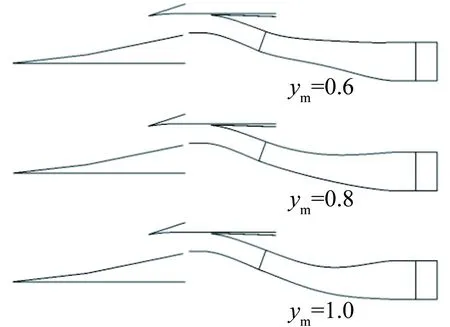
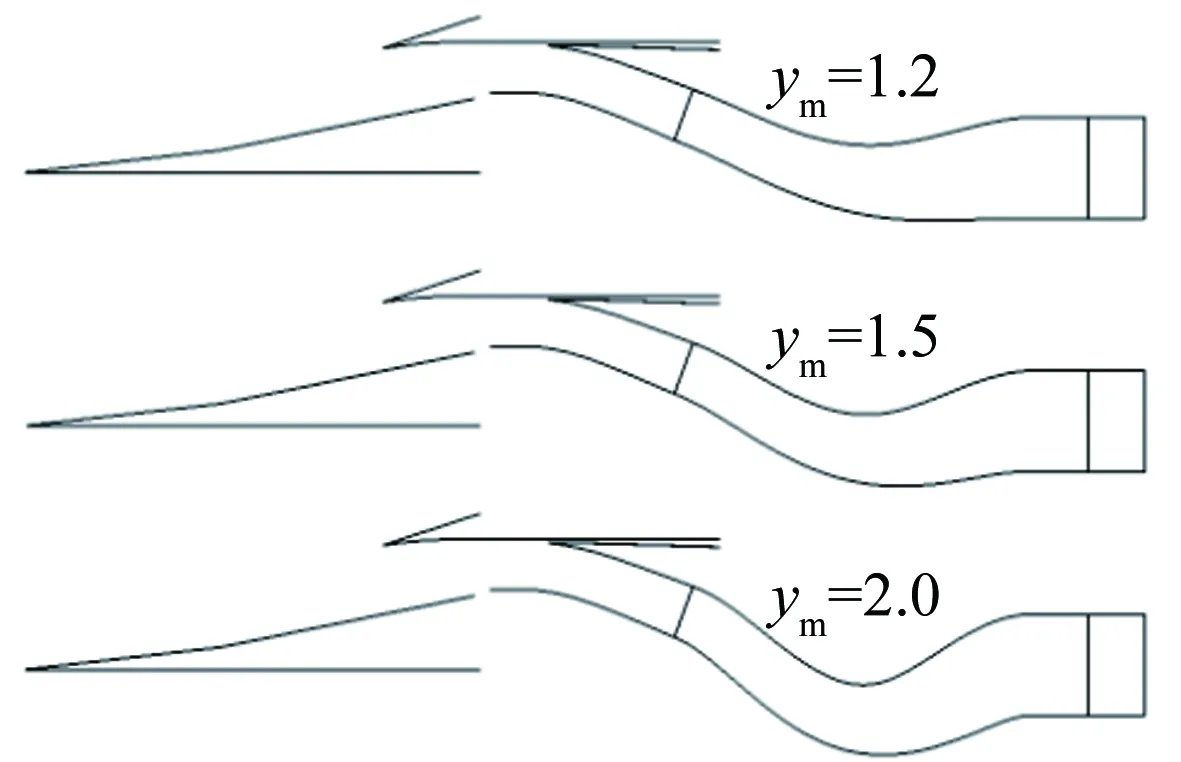
圖11 不同ym值下，渦輪發動機流道方轉圓擴壓段幾何造型

圖12給出了不同ym值情況下的渦輪通道方轉圓擴壓段出口總壓恢復系數等值圖。從圖中可見，隨著ym的增大，進氣道出口截面頂部的高總壓區逐漸被打散。當ym=1.5時，頂部的高總壓區已經完全消失，分散到兩側，同時中心的低壓區也分成兩個小的低壓區。

圖13給出了渦輪通道出口性能隨方轉圓擴壓段中心點ym的變化曲線，其中橫坐標表示方轉圓擴壓段中心點ym，縱坐標表示渦輪流道進氣道出口馬赫數(Mae)、總壓恢復系數(σ)以及周向畸變指數(DC60)。就本文設計的組合動力進氣道而言，在研究的參數變化范圍內，隨著方轉圓擴壓段中心點ym的增大，Mae保持在0.4～0.45之間，σ基本維持在0.8左右，變化不明顯；而DC60呈先減小后增大變化趨勢，在ym=1.5時達到最小值0.15，對比圖12可見，此構型下進氣道頂部的高總壓區已經完全消失，中心的低壓區也分成兩個小的低壓區，流場分布較為

均勻。在ym=2.0時，由于底部出現高總壓區，導致DC60升高至0.35。

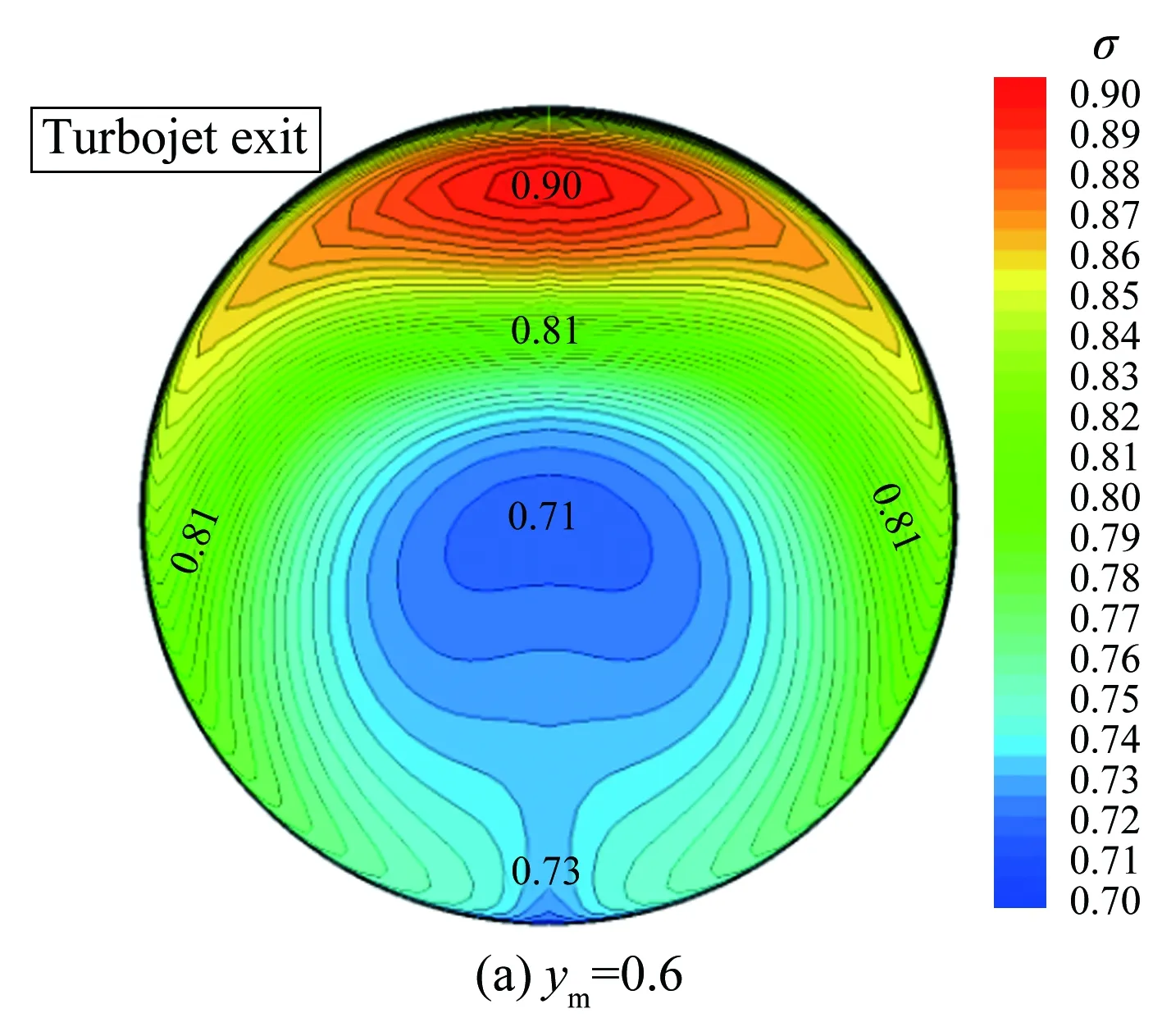
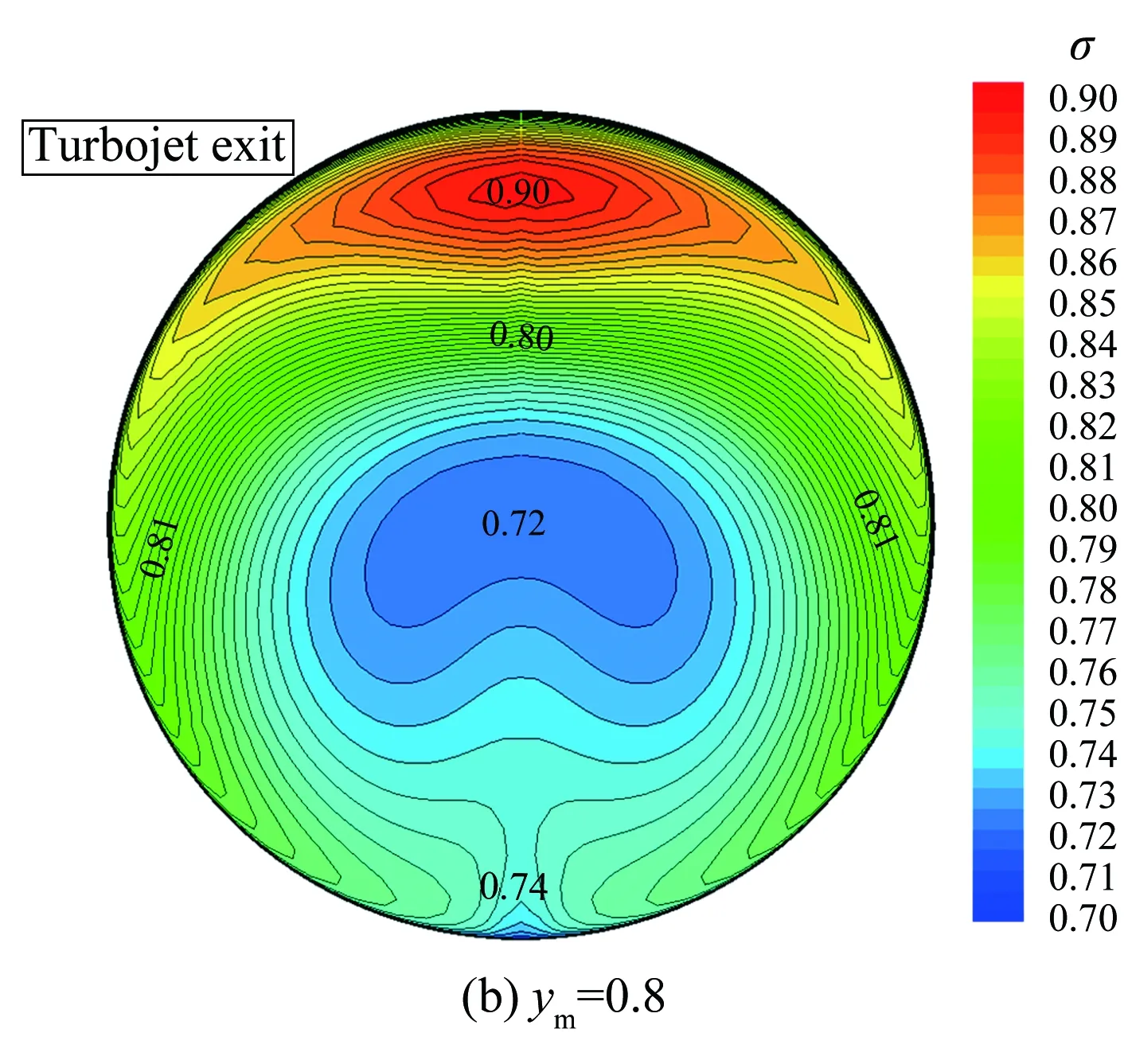
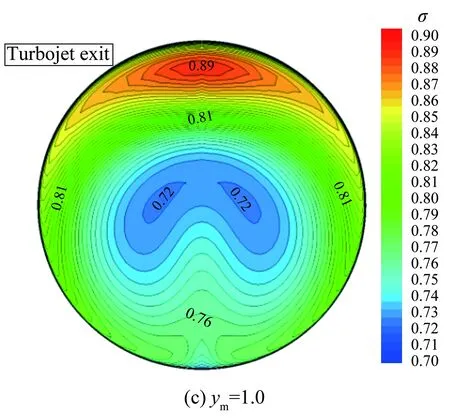
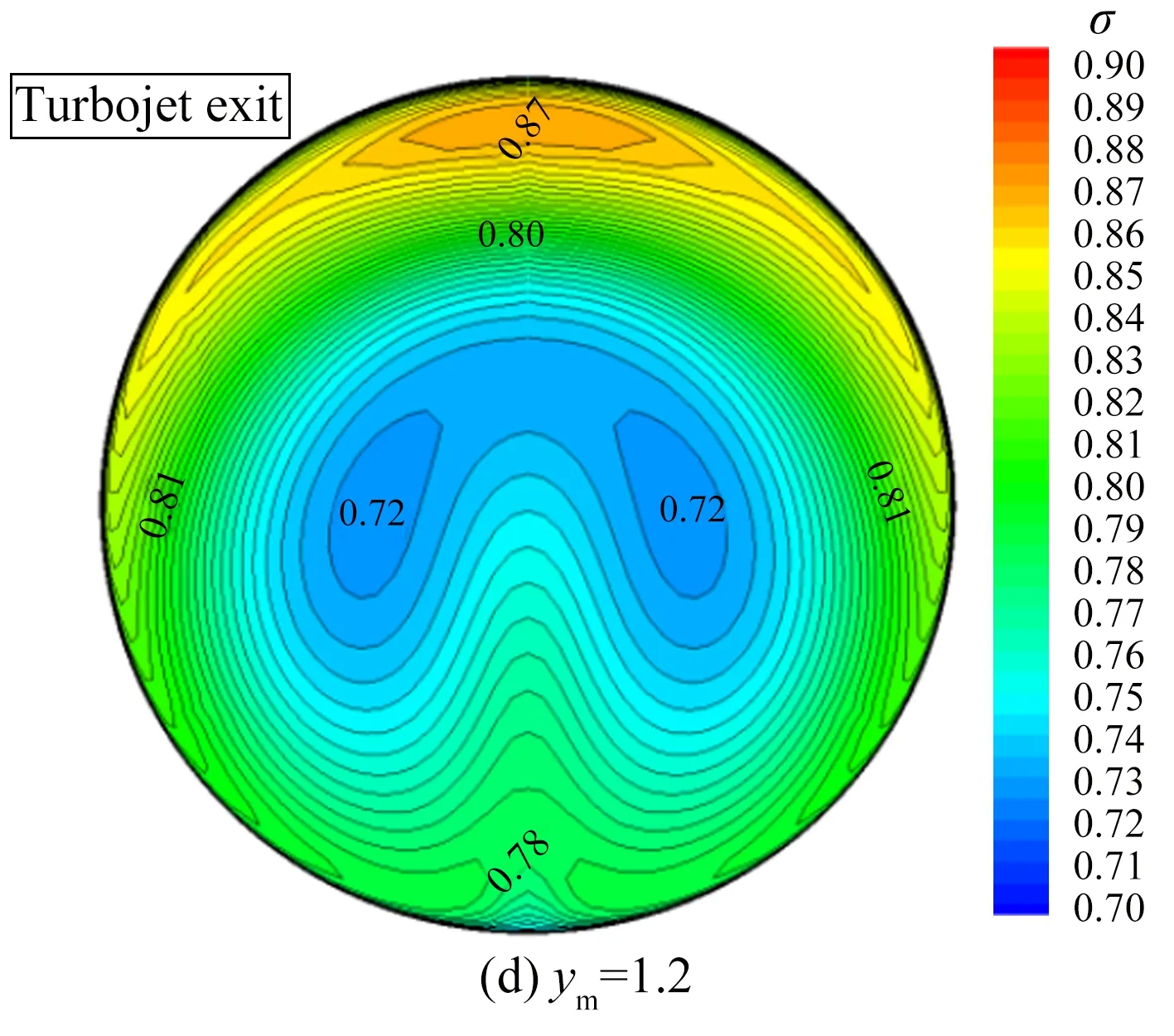
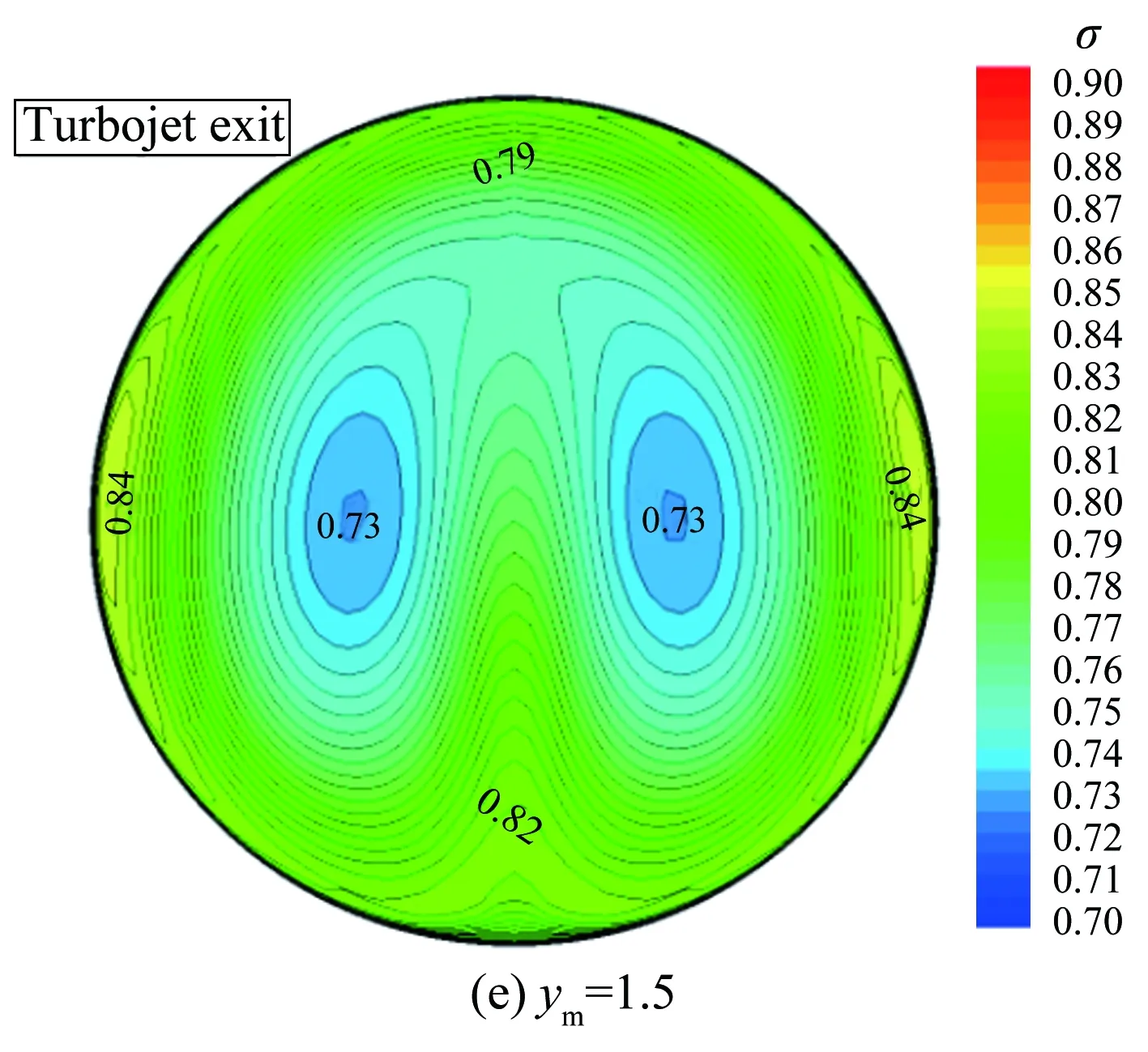
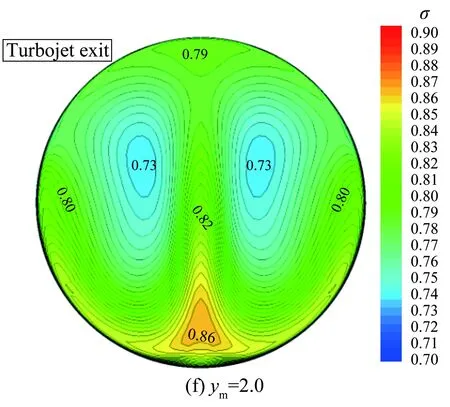
圖12 不同ym下，渦輪流道方轉圓擴壓段出口總壓恢復系數等值圖

Fig.12Thetotalpressurecontourofturbinediffuserexitsectionatdifferentymvalues

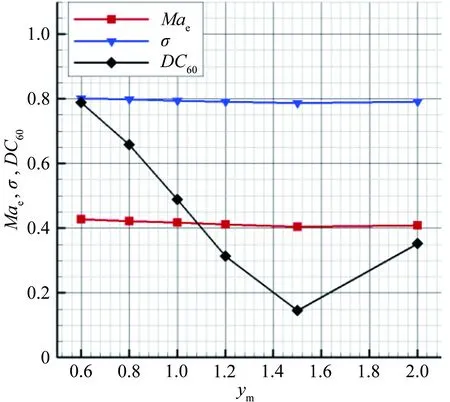
圖13 渦輪通道出口性能隨方轉圓擴壓段中心點ym的變化曲線

2.3.3方轉圓段沿程面積變化規律對進氣道氣動性能的影響

依據前文研究結果，選取方轉圓擴壓段幾何長度為3.0m、控制點ym=1.5的構型開展方轉圓段沿程面積變化規律對進氣道氣動性能的影響。具體研究中，選取先急后緩、先緩后急和緩急相當等3種方轉圓段截面沿程面積變化規律[16]。

表1給出了不同面積變化規律下渦輪流道出口截面馬赫數、總壓恢復系數、周向畸變指數的對比列表。從表中可見，就本文研究的組合動力進氣道幾何構型而言，先急后緩、先緩后急和緩急相當等3種變化規律對進氣道的氣動性能影響不明顯，但對進氣道出口截面的流場均勻程度影響較大。在先急后緩的沿程截面變化規律構型下，進氣道出口截面的畸變相對較低(約為0.13)。

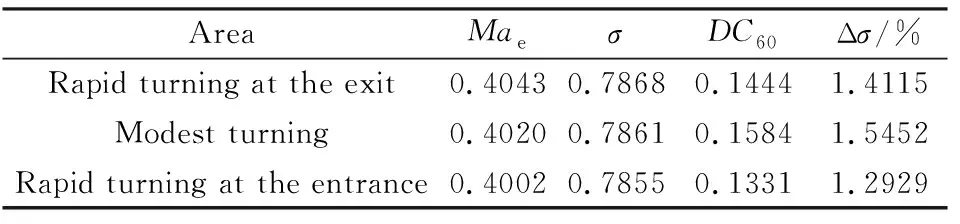
表1 不同方轉圓沿程截面面積變化規律下渦輪流道進氣道出口氣動性能Table 1 The parameters of ramjet engine at design point

綜合以上渦輪發動機流道方轉圓段典型幾何參數的規律化研究結果，就本文研究的組合動力進氣道而言，方轉圓段幾何長度選取為3m，方轉圓中心控制點ym=1.5，沿程截面面積變化規律為“先急后緩”。

2.4 TBCC進氣道氣動特性分析

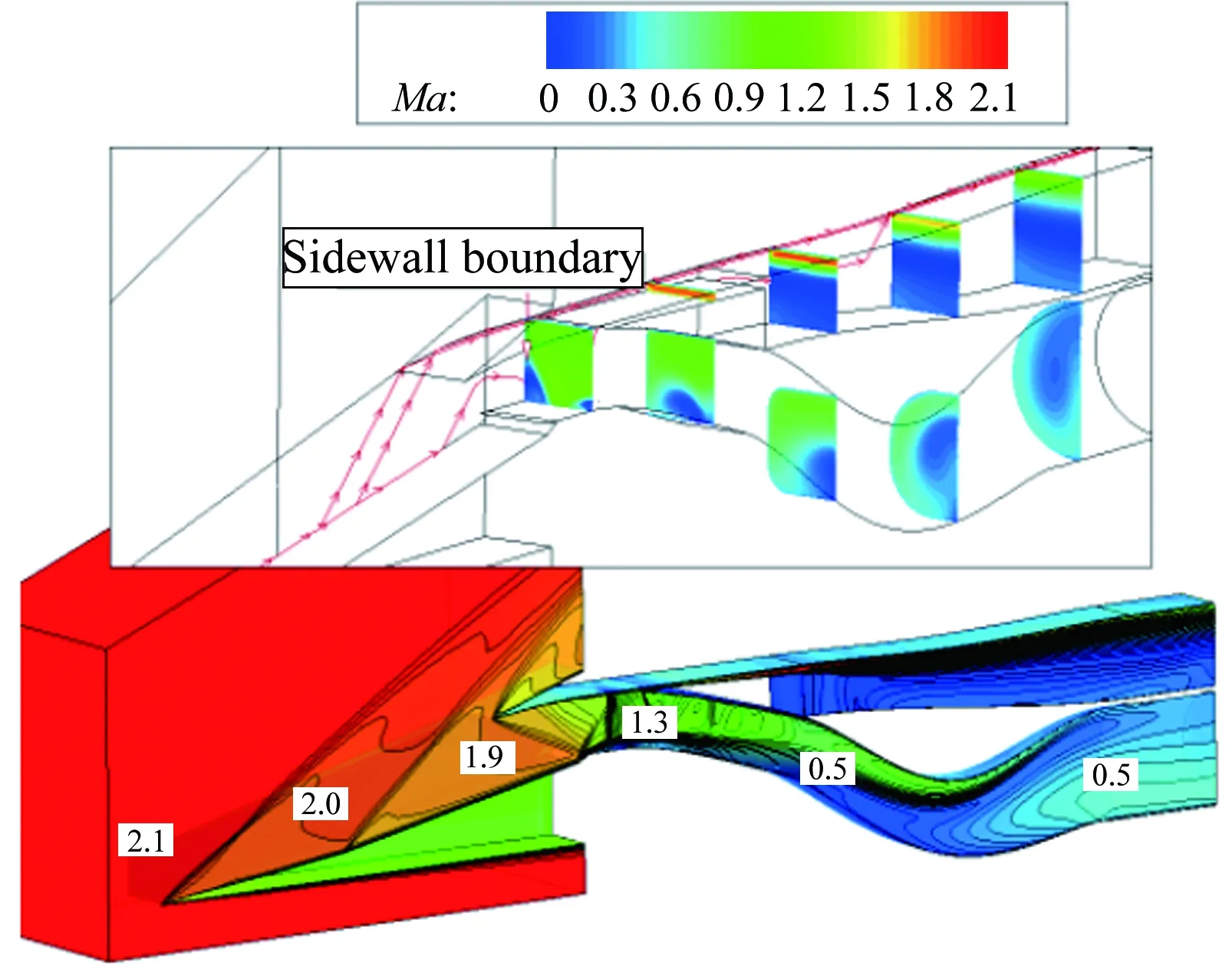
圖14給出了TBCC進氣道渦輪或沖壓工作模態下的進氣道流場圖(Ma1.5～4.0)。從圖中可知，Ma1.5時，結尾激波在進氣道唇口前；在其余馬赫數下，結尾激波均停留在喉道附近。其中，Ma1.5～2.2時，進氣道工作在渦輪模態下，沖壓通道作為旁路用于溢除唇罩一側的附面層；Ma2.5～4.0時，進氣道工作在沖壓模態下，渦輪通道作為旁路用于溢除壓縮面一側的附面層。

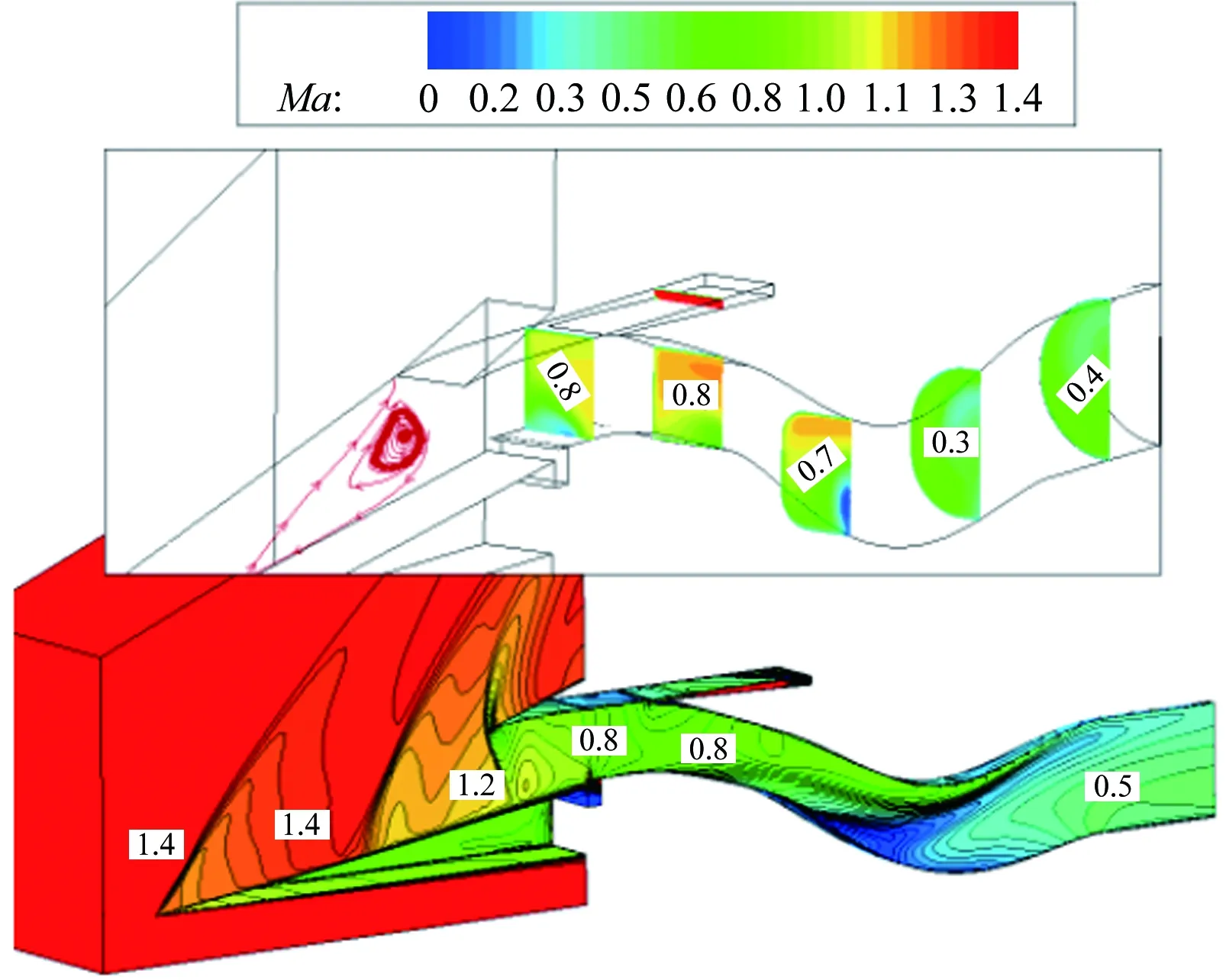
(a) Ma1.5

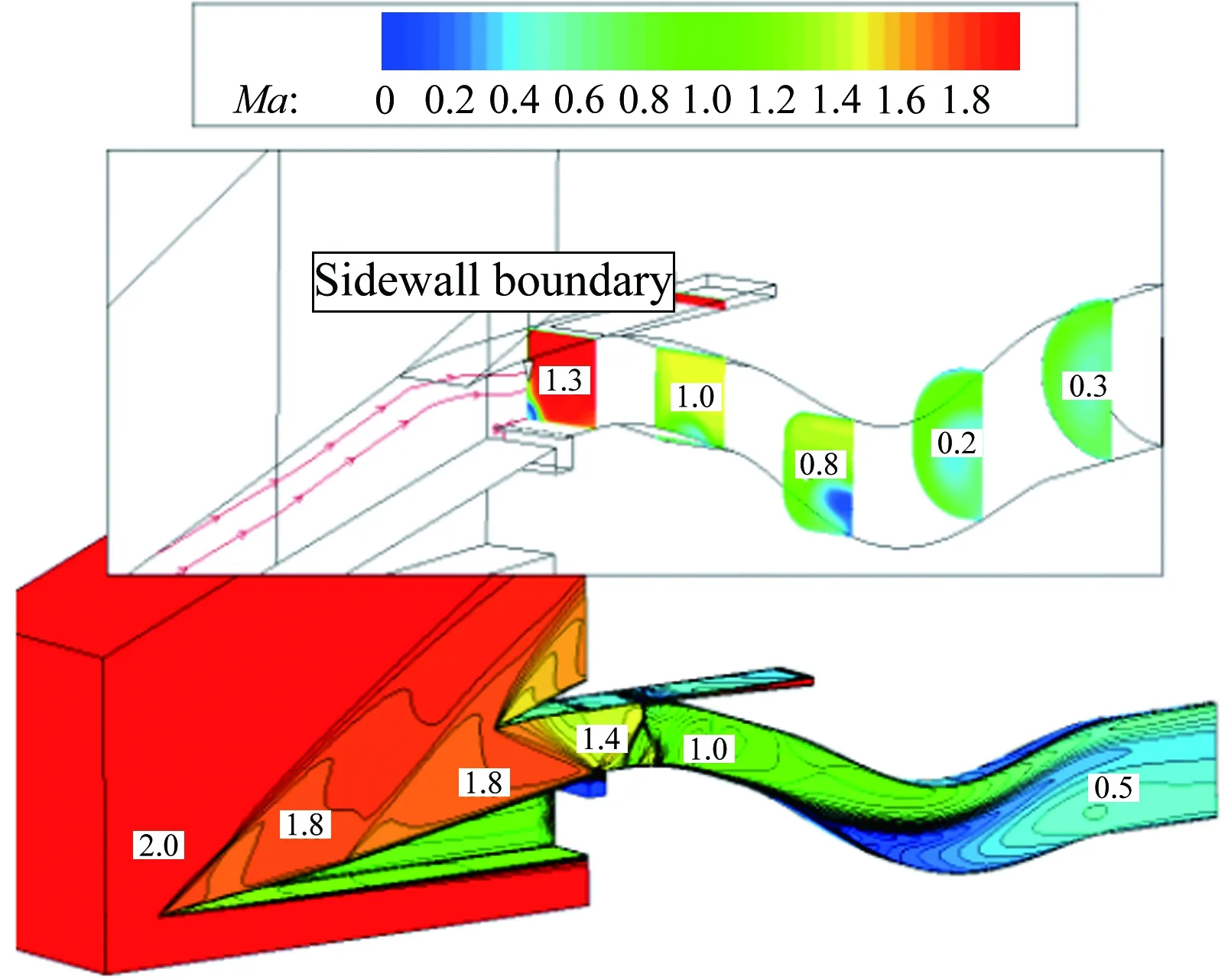
(b) Ma2.0

(c) Ma2.0

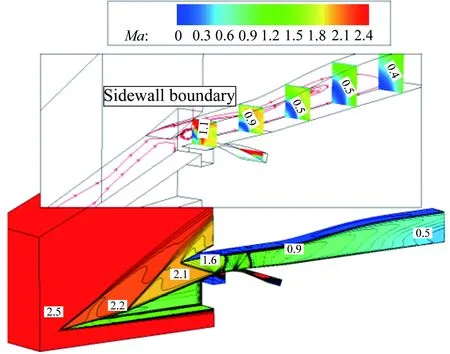
(d) Ma2.5

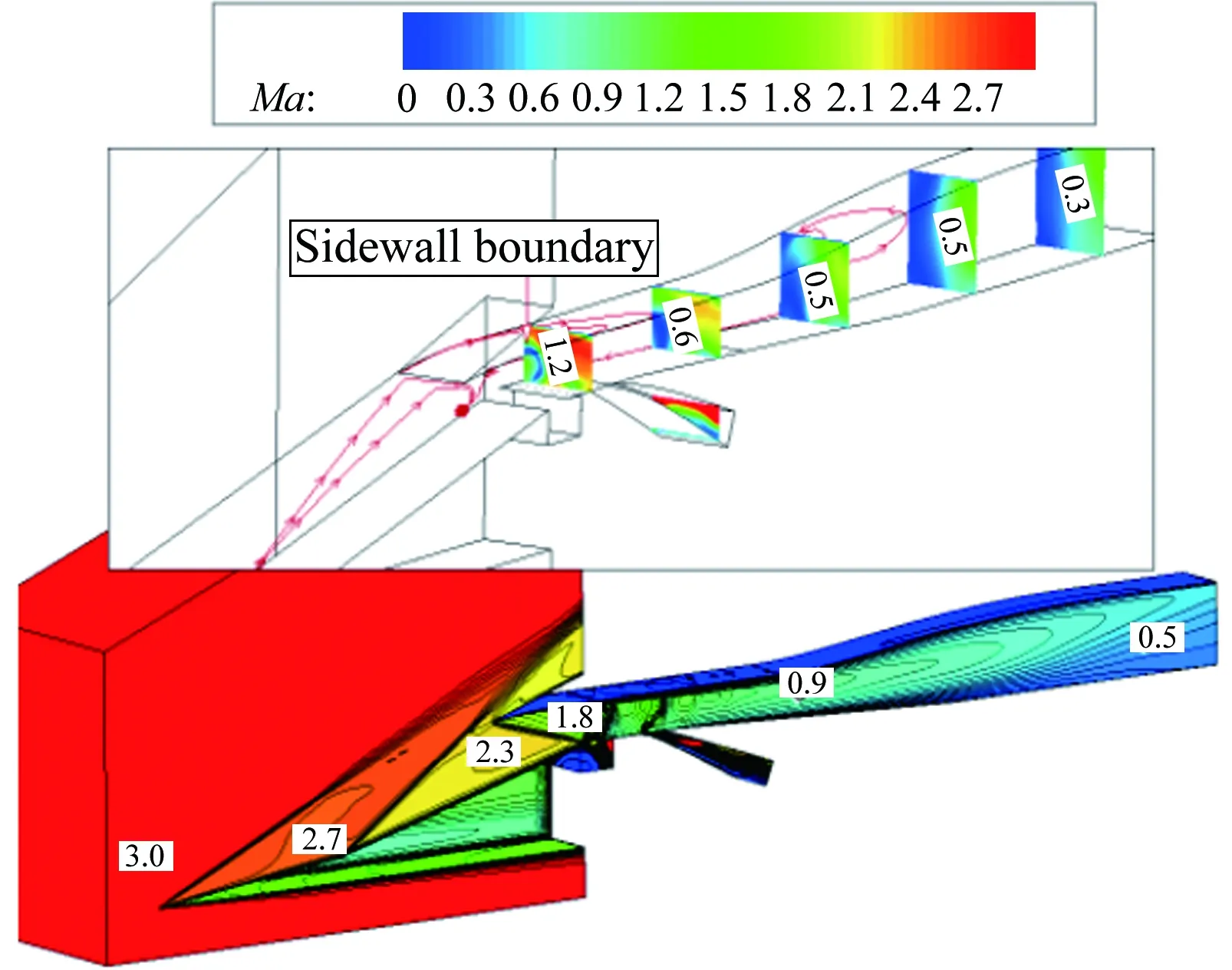
(e) Ma3.0

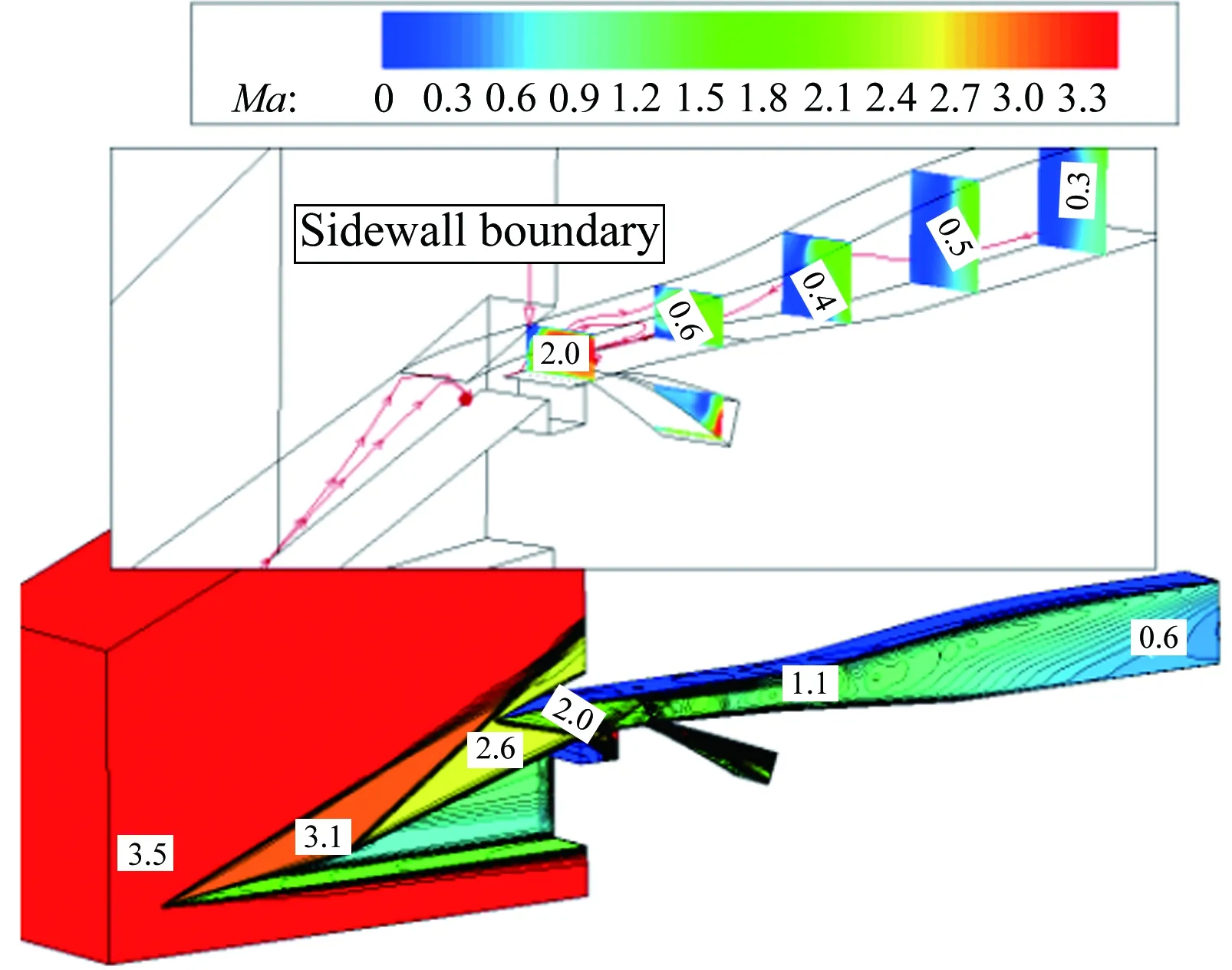
(f) Ma3.5

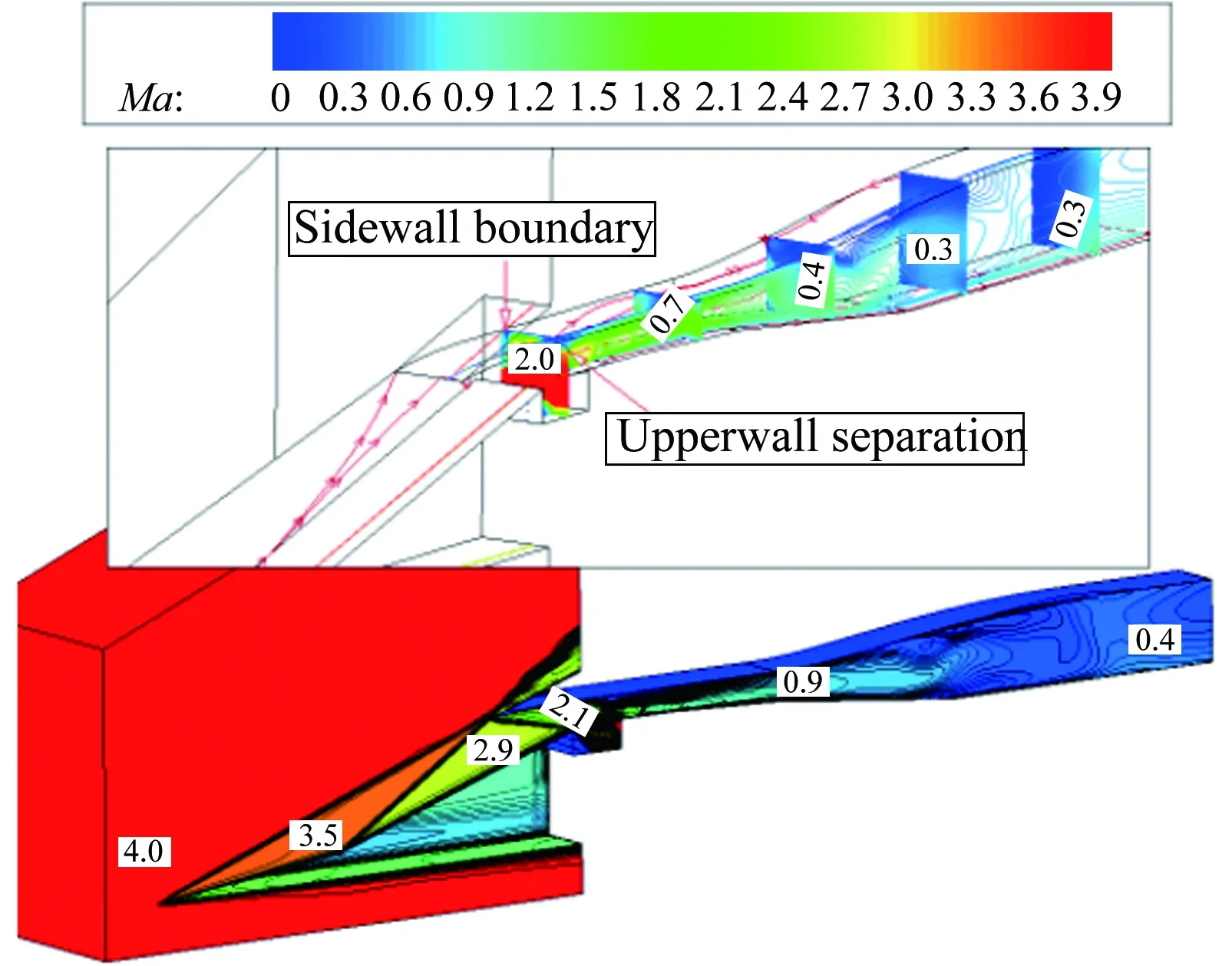
(g) Ma4.0

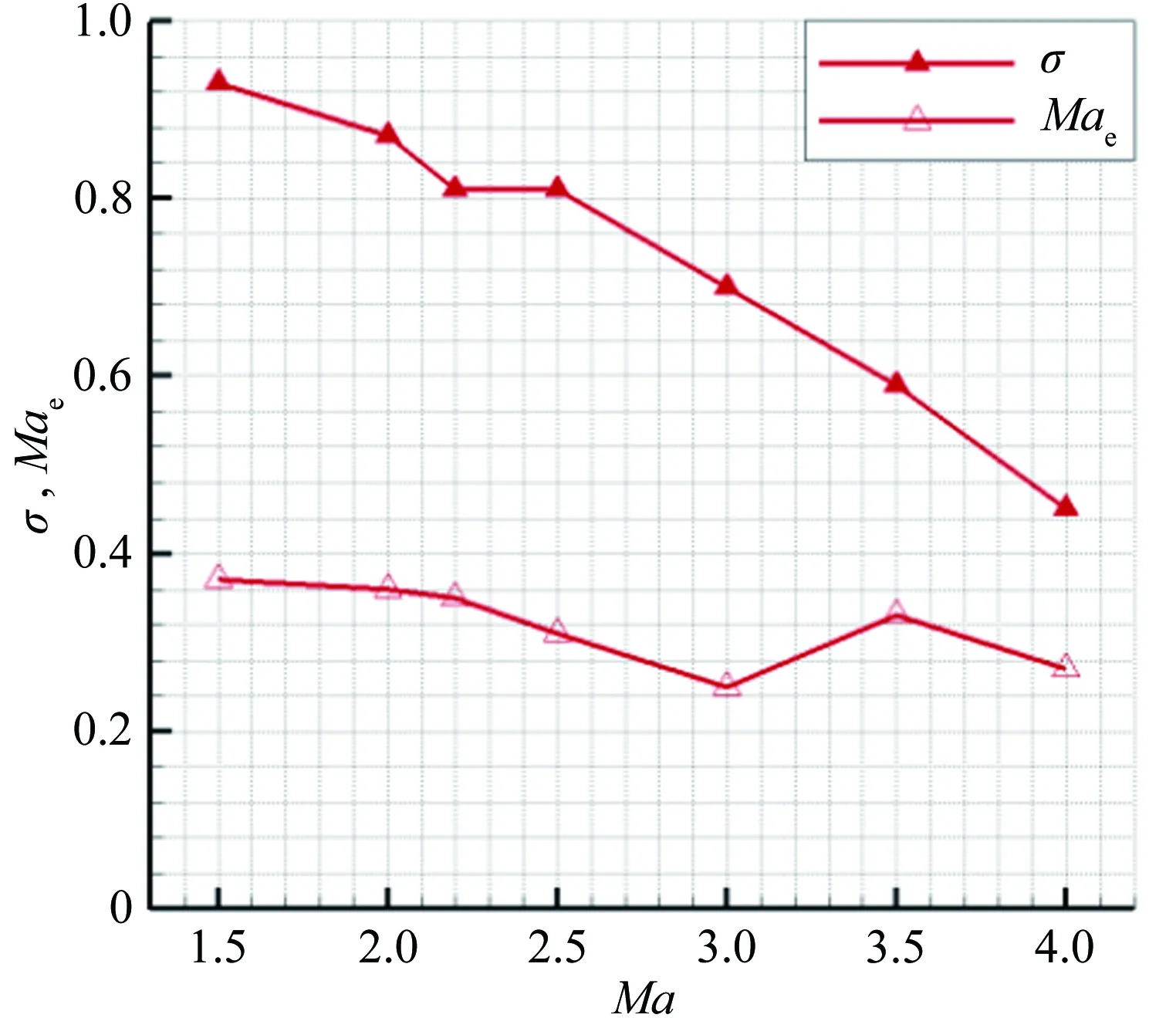
圖15(a)和(b)給出了數值仿真得到的流量及進氣道出口性能參數。從圖中可知：Ma1.5～4.0的流量均滿足需求；渦輪模態下進氣道出口馬赫數在0.3～0.4之間，沖壓模態下進氣道出口馬赫數在0.3左右；隨著來流馬赫數的增大，總壓恢復系數從0.92逐漸降低至0.45。

(a)

(b)

3 結 論

本文從TBCC推進系統總體性能分析需求出發，對一種Ma0～4范圍內的內并聯式TBCC變幾何進氣道方案設計開展了研究，得到如下結論：

(1) 從TBCC推進系統總體性能需求出發，給出了TBCC進氣道設計約束確定過程，結果表明：就本文給定的發動機參數而言，Ma4一級TBCC推進系統所需的進氣道捕獲面積在1.0m2左右，模態轉換馬赫數為2.2～2.5。

(2) 提出了一種基于上下平動式模態轉換裝置的TBCC可調進氣道氣動設計方案，給出了進氣道單自由度幾何調節機構方案及其幾何調節規律。

(3) 方轉圓段幾何長度、中心點ym值以及面積變化規律對進氣道出口總壓恢復系數及馬赫數影響較小，對進氣道出口流場的均勻度影響較大；當ym值從0.6增加至1.5時，總壓恢復系數和出口馬赫數分別降低了1.7%和5.3%，而畸變降低了81.4%。就本文研究的進氣道而言，選取方轉圓段幾何長度Ld=3m、中心控制點ym=1.5、沿程截面面積變化規律為“先急后緩”的設計較為適宜。

(4) 在Ma=4.0時，本文設計的可調進氣道總壓恢復系數為0.45；Ma=2.2時，進氣道的總壓恢復系數和畸變分別為0.79和0.15。