基于連續介質假設原理的膨化機螺桿摩擦阻力分析及參數優化

毛 君 魯 楠 謝 苗 盧進南 賈 凱

(遼寧工程技術大學機械工程學院，遼寧 阜新 123000)

擠壓膨化機因其獨特的加工方式和輸出結果，目前越來越受到飼料加工業和食品制造業的重視。通過擠壓膨化技術處理的原料利用率通常能夠達到80%甚至更多，因此大大地提高了產品的生產率和質量[1-2]。擠壓加工技術最早出現在19世紀70年代的英國，并逐漸被應用到橡膠工業中[3]，直到1936年第一臺單螺桿擠壓膨化機首次被意大利人應用于方便谷物食品生產中[4]。現如今擠壓膨化加工技術己經非常普遍地應用于膨化玉米、大豆等谷物食品和飼料產品。但是如何不斷提高膨化機的生產效率、降低能耗一直是國內外學者探討的重點課題，現已成為膨化機研究的熱點和關鍵問題。

近年來相關學者對如何優化擠壓膨化機的設計進而提高設備的生產效率降低能耗進行了大量研究，但目前對擠壓膨化機的優化研究仍略有局限性。張魁學等[5]通過正交多項式回歸設計法研究分析了螺桿轉速、物料溫度以及工作壓力等因素對機器生產率、耗電量、膨化率等的影響。鄒鳳等[6]利用動量定理推導出模孔徑長比、物料與模孔壁間摩擦因數和模孔兩端壓強差三者間理論關系式。李少華等[7]以油菜籽為原料采用響應面分析法研究模孔直徑、膨化溫度、喂料速度和物料含水率對膨化預榨餅殘油質量分數的影響規律，并對參數進行工藝優化。楊凱等[8]建立了同向嚙合雙螺桿擠壓膨化機共軛型螺桿的力學模型及有限元模型，并運用有限元分析方法對不同螺距和內外徑比(SAR)的螺桿進行了應力分析。這些研究多是通過試驗分析方法從擠壓膨化設備的模孔幾何參數、物料含水率、螺桿轉速、膨化溫度、喂料速度等工藝參數對膨化機進行完善優化，進而提高擠壓膨化機的生產效率降低能耗，而沒有通過建立螺桿的摩擦力學模型然后運用數值分析法直觀地分析螺桿多項結構參數對摩擦阻力的影響。鑒于目前對螺桿結構參數與螺桿摩擦磨損之間關系的研究缺陷，本研究將結合遼寧祥和農牧實業有限公司生產的9P-150B型秸稈膨化機，創新性地運用連續介質假設原理建立螺桿旋轉擠壓物料的摩擦阻力模型，進而對單螺桿秸稈膨化機的關鍵部件螺桿進行系統的摩擦受力分析，以降低有害摩擦進而提高螺桿的應力強度與膨化機的實用性能。

1 螺桿的構形要求及結構參數

1.1 螺桿的構形要求

針對擠壓物料任務的螺桿主要功能：① 具備合理的結構參數以減小物料在擠壓過程中與螺桿產生的磨損；② 具備良好的結構形態使物料在螺桿槽內能夠得到充分的加工；③ 具備足夠的剛度和強度以滿足擠壓物料過程中沖擊振動等工況要求。本文主要針對物料與螺桿間產生的有害摩擦進行研究[9]。

1.2 螺桿的結構參數

對螺桿的摩擦阻力進行研究需要對其結構參數進行定義，以便建立其摩擦阻力的數學模型，螺桿結構參數見圖1。

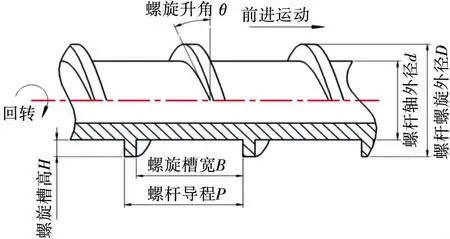
圖1 螺桿結構參數示意圖Figure 1 Schematic diagram of screw structure parameters

2 螺桿摩擦阻力分析及其力學模型的建立

秸稈在膨化機內的輸送及擠壓是一個相當復雜的過程，若運用連續介質假設原理進行理論分析，需要做出以下幾點基本假設：

(1) 假定螺槽中運動的物料為可壓縮的連續運動體，密度僅沿螺槽方向有變化。

(2) 螺桿中的物料與螺槽底面、兩個側面和機筒內表面同時緊密地接觸，物料和螺槽各表面之間的摩擦力只取決于法向應力而與物料的位置和運動無關。

(3) 假設料筒在圓周方向上作勻速旋轉運動，機筒相對于物料微元的運動方向角為φ，且忽略該夾角沿著物料運動方向的變化。

(4) 軸向應力(壓力)和法向應力只沿物料運動方向變化。

基于上述的基本假設和分析，螺桿在旋轉過程中受到物料產生的復雜摩擦力便可簡化分成簡單的兩部分：① 物料在螺旋槽底面上產生的摩擦阻力；② 螺旋槽前后側面與物料間產生的摩擦阻力[10]。

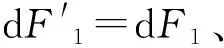
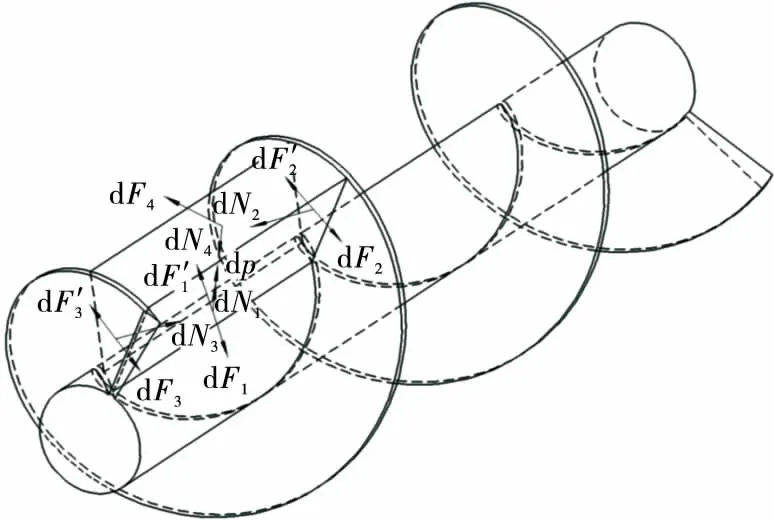
圖2 物料在螺桿槽內的受力Figure 2 The force of material in the groove

2.1 物料在螺旋槽底面上產生的摩擦阻力

螺旋槽底面上物料微元產生的摩擦阻力：

dF1=fsdN1，

(1)

式中：

fs——物料與螺桿間的摩擦系數；

dF1——螺旋槽底面對物料微元的摩擦力，N；

dN1——螺旋槽底面對物料微元的支持力，N。

2.1.1 外機筒內表面對物料微元的壓力 物料微元受到外機筒內表面的壓力：

dN4=pBcosθdL，

(2)

式中：

p——外機筒作用于物料上的壓力，Pa；

B——螺槽軸向寬度，m；

θ——螺桿螺旋升角，(°)。

查閱文獻[12]可得，外機筒作用于物料上的壓力與物料在加料斗處的初壓力有關：

p=p0eτL，

(3)

式中：

L——計算段的螺槽長度，m；

p0——物料在加料斗處的初壓力，Pa；

τ——比例系數。

由文獻[12]得：

(4)

(5)

式中：

D——螺桿螺旋外徑，m；

H——螺旋徑向高度，m；

fb——物料與機筒間的摩擦系數；

φ——物料微元相對于機筒運動的方向角，(°)。

2.1.2 物料微元旋轉運動時受到的離心力 物料在高速旋轉時產生的離心力：

(6)

式中：

ρ(z)——物料密度，kg/m3；

ω——物料在螺桿螺旋槽內的轉速，r/min。

式(7)中螺旋微元長度dL與軸向微元距離dz的關系：

(7)

2.1.3 螺旋槽底面對物料微元的支持力 由圓周運動受力平衡得：

dp+dN1=dN4。

(8)

所以

dN1=dN4-dp。

由式(1)～(8)得到：

(9)

2.2 物料在螺旋槽側面上產生的摩擦阻力

物料微元在螺旋槽側面上產生的摩擦阻力可分為前后兩部分，分別為dF2與dF3。

dF2=fsdN2，

(10)

dF3=fsdN3，

(11)

dN3=dN2+dN0。

(12)

其中dN0為螺旋推力，螺旋前側面法向作用力：

dN2=pHdL。

(13)

2.2.1 螺旋槽前側面對物料微元的摩擦力 由式(3)、(7)、(10)、(13)得：

(14)

2.2.2 螺旋推力的計算 求F3需要知道dN0。將物料微元受到的所有力分解成沿軸向方向與沿螺紋螺旋方向，由于物料微元在螺旋槽中的運動是穩定的，因此沿軸向方向的所有分力的總和等于零，即

(15)

將式(12)帶入式(15)得

dN0=dF4sin(φ+θ)。

(16)

又物料微元外表面上機筒產生的摩擦力：

dF4=fbdN4。

(17)

將式(17)帶入式(16)得

dN0=fbdN4sin(φ+θ)。

(18)

2.2.3 螺旋槽后側面對物料微元的摩擦力 由式(3)、(4)、(8)、(11)、(12)、(13)、(18)得:

(19)

由前述分析可知螺桿擠壓物料受到的摩擦阻力為式(9)、(14)、(19)之和，即

(20)

3 螺桿結構參數與摩擦阻力關系影響分析

根據文獻[13]可知,決定膨化機螺桿結構的參數主要有螺旋外徑D、軸向槽寬B、徑向齒高H以及螺旋升角θ。由式(20)可以很容易看出，螺桿受到的摩擦阻力隨著螺桿螺旋外徑D的增加而減少。螺旋外徑增大說明螺桿在高速旋轉下物料受到的離心力變大，導致螺桿底面對物料的擠壓力變小，二者之間的摩擦力變小。而螺桿的其他參數(軸向槽寬B、徑向齒高H、螺旋升角θ)對螺桿所受摩擦阻力的影響不能夠輕易看出。因此采用Matlab分析其他參數對螺桿所受摩擦力造成的影響。

3.1 螺槽軸向寬度與摩擦阻力的關系

通過試驗可以獲得螺桿和機筒與物料間的摩擦系數fs=fb=0.3。則由式(20)可以得出，螺桿受到物料的摩擦阻力與螺桿軸向槽寬的數學關系如式(21)。

Ff=f(B)=F1(B)+F2(B)+F3(B)。

(21)

如圖3所示，當螺槽軸向寬度增大時，螺桿受到的摩擦阻力呈增大趨勢。螺槽軸向寬度增加說明螺旋槽容納的物料更多，物料與螺桿的接觸面積變大，摩擦阻力自然變大。但從圖3中可看出，螺槽軸向寬度對螺桿受到的摩擦阻力的影響較小。

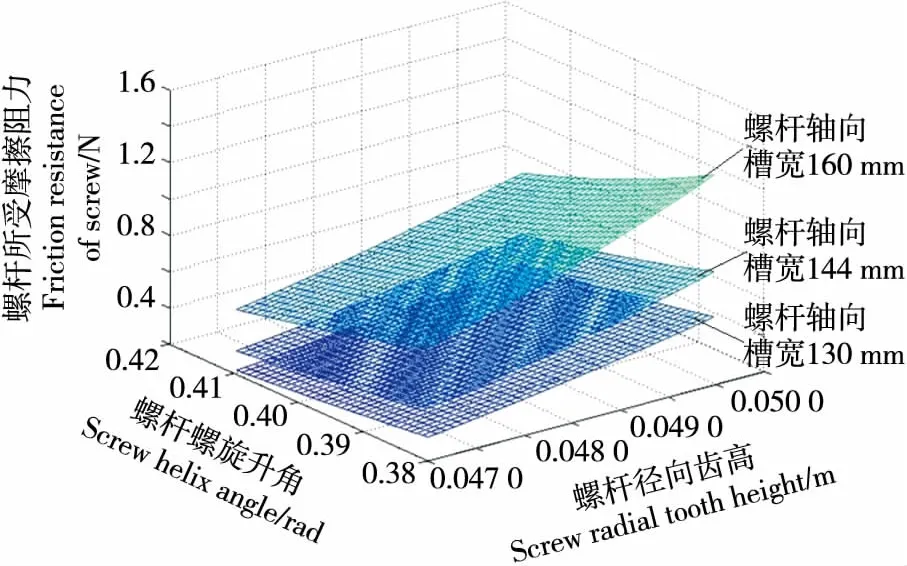
圖3 螺桿摩擦阻力隨螺旋升角和徑向齒高變化關系

圖3 Relationship between screw friction resistance and screw rise angle and radial tooth height

3.2 螺桿徑向齒高與摩擦阻力的關系

由式(20)可以得出，螺桿受到物料的摩擦阻力與螺桿徑向齒高的數學關系見式(22)。

Ff=f(H)=F1(H)+F2(H)+F3(H)。

(22)

由圖4可知，螺桿所受摩擦力的絕對值隨徑向齒高的增加而增加。螺桿徑向齒高增加，說明螺槽內的物料與螺槽側壁的接觸面積增大，因此螺桿所受摩擦力增大。相比于螺槽軸向寬度，螺桿徑向齒對螺桿受到摩擦力的影響相對較明顯。

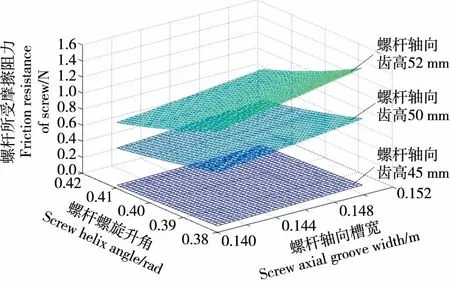
圖4 螺桿摩擦阻力隨螺旋升角和螺旋外徑變化關系

圖4 Relationship between screw friction resistance and screw rise angle and screw outer diameter

3.3 螺桿螺旋升角與摩擦阻力的關系

由式(20)可以得出，螺桿受到物料的摩擦阻力與螺桿螺旋升角的數學關系見式(23)。

Ff=f(θ)=F1(θ)+F2(θ)+F3(θ)。

(23)

螺桿螺旋升角的大小影響機構工作時螺桿對物料的加工情況，螺旋升角過小時對物料的擠壓比較充分，但需要消耗很大功率才將物料排出；螺旋升角過大時物料填充率不高，且物料受到的擠壓不夠充分。由圖5可知，螺桿所受摩擦力隨螺旋升角的減小而增大，且升角越小變化率越大，因為螺旋升角減小導致螺旋槽對物料的軸向分力變大，而徑向分力減小，進而由軸向擠壓力而產生的摩擦力隨之變大。相比于軸向槽寬與徑向齒高，螺旋升角的變化是對螺桿受到的摩擦力影響最為明顯的一個因素。

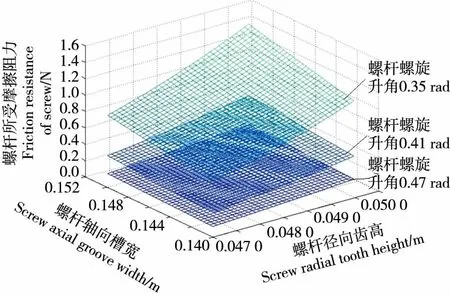
圖5 螺桿摩擦阻力隨徑向齒高和螺旋外徑變化關系

圖5 Relationship between screw friction resistance and radial tooth height and screw outer diameter

4 膨化機螺桿結構參數優化

4.1 目標函數

通過前文的分析可知，螺桿受到物料產生的摩擦力與螺桿的多項結構參數均有不同程度的關系，因此運用Matlab的optimization工具箱將螺桿的所有結構參數均考慮在內，以式(20)中各個結構參數乘以相應的權重系數所得的式(24)為目標函數，對螺桿進行結構優化使物料對螺桿產生的摩擦阻力有所降低。

Ff(X)=F(η1D，η2θ，η3B，η4H)，

(24)

式中：

η1——螺桿螺旋外徑權重系數；

η2——螺桿螺旋升角權重系數；

η3——螺桿軸向槽寬權重系數；

η4——螺桿徑向齒高權重系數。

4.2 約束條件

建立螺桿結構優化的設計變量見式(25)。

X=(x1x2x3x4)T=(DθBH)T，

(25)

式中：

D——螺桿螺旋外徑，m；

θ——螺桿螺旋升角，(°)；

B——螺桿軸向槽寬，m；

H——螺桿徑向齒高，m。

(1) 在實際生產中，彎曲力和扭矩力同時作用在螺桿上，但扭矩力要大于彎曲力，由材料力學可得：

(26)

式中：

[τ]——許用剪切應力，取340 MPa；

Nmax——電機最大額定功率，取110 kW；

μ——機械效率，取0.923；

nmax——螺桿最高轉速，取157.1 r/min。

(2) 根據實際生產中對生產效率的要求可給出螺桿螺旋外徑大致范圍：

0.1≤D≤0.2。

(27)

(3) 螺旋升角范圍：

10°≤θ≤30°。

(28)

(4) 由螺旋槽軸向寬度小于螺桿導程可得槽寬范圍：

0.1≤B≤P=πtanθ(D-H)。

(29)

(5) 螺桿徑向齒高小于螺旋外半徑，則齒高范圍：

(30)

4.3 螺桿結構參數優化數學模型

根據目標函數及參數約束條件的分析，可以將膨化機螺桿的尺寸參數優化問題確定為非線性約束的多目標最優化問題，選用Matlab中optimization 工具箱里的 fminimax函數求解最優值，經整理后螺桿結構參數優化數學模型為：

minFf(X)=F(η1D，η2θ，η3B，η4H)，

(31)

X=(x1x2x3x4)T=(DθBH)T。

(32)

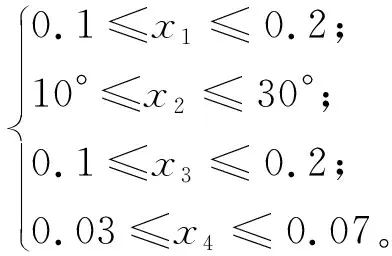
線性不等式約束:2x4-x1≤0。

非線性不等式約束：

x3-πtanθ(x1-x4)≤0；

綜合分析螺旋外徑、螺旋升角、軸向槽寬與徑向齒高在優化目標中的變化趨勢及范圍，在統一數值量級的條件下運用層次分析法[14]在Matlab中經多次仿真計算，選定權重系數η1=0.75、η2=0.05、η3=1.00、η4=1.23。

4.4 優化計算及結果

利用Matlab對優化過程計算，經優化取整后得到螺桿的結構參數D、θ、B、H分別為153 mm，24.29°，141 mm，48 mm。優化后螺桿受到物料產生的摩擦力為0.975 2 N，比之前降低了51.38%。表1為優化前后結果對比。

5 螺桿受到物料摩擦力的ANSYS分析驗證

根據優化后的參數對之前的螺桿三維有限元模型進行修改，然后分別將修改前后的有限元模型導入到Ansys Workbench中進行靜力學分析，根據前述的螺桿受力分析模擬物料在螺桿槽內運動產生的摩擦力對螺桿造成的影響，對上述優化結果進行仿真驗證。

表1 優化結果對比Table 1 The comparison results of optimization

圖6為螺桿優化前后的等效應力云圖。從圖6中可看出，螺桿的表面應力由機頭向固定端逐漸變大，螺紋上的應力是沿著螺旋線分布的，螺紋加載面上的應力值從螺紋根部向螺紋外緣逐漸增大，螺紋根部的應力值最大是由于彎矩及螺桿結構突變引起的應力集中。優化前后物料與螺桿之間由于摩擦產生的最大應力分別為6 368.7，2 039.6 MPa，優化后螺桿的應力有明顯的下降，說明前述優化結果具有一定的可靠性。

圖7為螺桿優化前后的變形云圖。從圖7中可看出，最大位移變形出現在受力端面，且從機頭向固定端方向變形量逐漸減小。優化前后由于摩擦力對螺桿產生的最大變形值分別為21.928 0，8.197 6 mm，可看出優化后因摩擦產生的變形量對螺桿的影響有明顯的改善，并不會因變形過大而導致與套筒內壁之間發生劇烈的摩擦和碰撞作用，致使螺桿與套筒的間隙過大不能正常擠出物料而報廢，因此優化后的螺桿在機構運行過程中的使用性能更加趨于平穩。

圖6 螺桿優化前后等效應力分析云圖Figure 6 The equivalent stress analysis cloud chart before and after optimization of screw

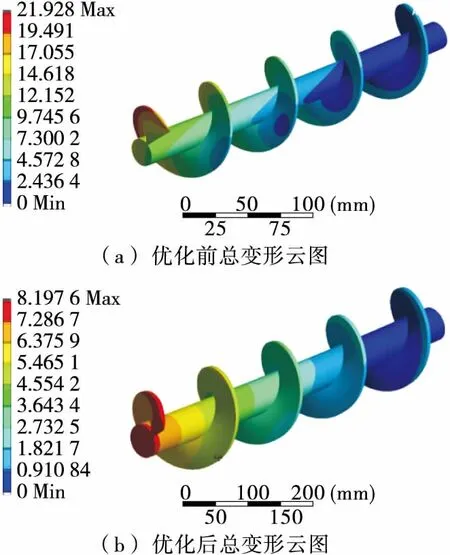
圖7 螺桿優化前后總變形分析云圖

圖7 The total deformation analysis cloud chart before and after optimization of screw

綜上，通過對優化前后的螺桿模型進行有限元仿真，得出該螺桿的模擬仿真結果基本能說明Matlab的數值優化結果的正確性，進一步表明所建立的螺桿受到物料摩擦阻力的力學模型的準確性。

6 結論

(1) 本研究基于連續介質假設原理，從螺桿結構參數角度建立單螺桿膨化機螺桿旋轉擠壓物料的摩擦阻力模型，得到摩擦阻力隨螺桿的螺旋外徑與螺旋升角的增大而減小，隨著螺桿的軸向槽寬與徑向齒高的減小而減小，且螺旋升角的變化對摩擦力的影響最為明顯。

(2) 以螺桿受摩擦阻力為目標函數優化螺桿的各項結構參數，結果表明在滿足膨化機生產效率的要求下優化后的摩擦阻力降低了51.38%。

(3) 對優化前后的螺桿進行有限元分析驗證，結果表明優化后螺桿的應力與變形均有所改善，進一步表明所建力學模型的準確性。

通過優化分析計算出了單螺桿膨化機在物料加工過程中使螺桿受到物料的摩擦磨損最小時的最優結構參數，基于該方法可以在保證膨化機中主要零部件——螺桿的可靠性及壽命的前提下，提高膨化機的生產效率，改善產品的使用性能，為產品的優化、性能評價提供了一種全新的手段。