三維角度域網絡干擾的空間選擇特性
杜得榮,曾孝平,簡 鑫,楊 凡,2,陳 禮
(1. 重慶大學 通信工程學院,重慶 400044;2. 重慶金美通信有限責任公司,重慶 400044)
大規模無線通信網絡(如車聯網、無線傳感器網絡和密集部署網絡等)由數量眾多的節點構成,對稀缺的頻譜資源需求極大. 高密度頻譜空間復用是提高頻譜利用率的主要手段,然而這會帶來嚴重的網絡干擾[1-2]. 三維智能天線和波束賦形技術的快速發展為解決網絡干擾問題提供了有效手段,而網絡干擾的空間選擇特性對智能天線和波束賦形的設計和性能評估有著重要影響. 因此,在三維空間角度域,對網絡干擾的統計特性進行研究可為干擾避免和消除技術提供理論支撐.
目前,對網絡干擾進行建模和分析的文獻較多,但大多文獻是基于隨機幾何理論,分析接收端總干擾包絡或功率的大小及概率密度[3-4],而對干擾空間選擇特性建模和分析的研究很少. 由于大規模無線通信網絡包含大量空間分離節點,任意接收端的干擾信號數目眾多,干擾信號可類似于信道建模中多徑散射信號,因此,空間多徑信道建模理論可為網絡干擾統計特性的研究提供重要視角. 文獻[5]提出了二維多徑成型因子理論,用來描述多徑衰落角度域空間選擇特性,即用三個成型因子(角擴展、角收縮和最大衰落方位角方向)對本地區域的任何非全向的多徑波束分布進行定量分析,具有物理意義明確,表述簡單的優點. 文獻[6]基于二維多徑成型因子理論提出了三維多徑成型因子理論,運用角擴展、俯仰角收縮、45°俯仰角收縮、方位角收縮、45°和0°俯仰角下最大衰落方位角方向六個因子表征信道的角度域空間選擇特性. 二維及三維多徑成型因子理論為研究大規模網絡干擾的空間選擇特性提供了有力工具,文獻[7-8]就基于二維成型因子理論對二維空間網絡干擾進行了角度域建模,并分析了干擾的統計特性. 由于通信網絡各節點的高度不同,信號傳播也會受到三維空間中的散射體散射,因此,網絡干擾功率分布于三維空間中. 然而,已有文獻尚未就三維角度域網絡干擾模型及其統計特性展開研究.
針對已有文獻的研究不足,筆者面向包含大規模空間分離節點的無線通信網絡,提出一個三維高斯干擾空間分布模型,并給出相應的干擾功率角度譜密度函數. 然后,基于三維成型因子理論,推導出了干擾關鍵空間統計特性的閉合表達式. 最后,仿真分析了三維角度對干擾功率角度譜密度函數和關鍵空間統計特性的影響,研究結果可簡化三維智能天線和波束賦形技術的設計和評估.
1 三維高斯干擾空間分布模型和干擾功率角度譜密度
1.1 三維高斯干擾空間分布模型

圖1 三維高斯干擾空間分布模型
圖1展示了接收端干擾來波的功率分布,RX為接收端;干擾者(基站或其他終端節點)與RX具有視距路徑時,I為干擾者,干擾者與RX無視距路徑時,I為干擾信號到達RX前的最后一個散射體;S為干擾所分布的三維空間(灰色區域);α∈ [0,2π]為干擾來波方位角,β∈ [0,π/2],為干擾來波俯仰角;r為I到RX的距離;σ為高斯分布標準差,根據高斯分布3σ原則,r的最大有效值為3σ.
三維高斯干擾空間分布模型基于以下假設和設定:
(1) 距離越遠的干擾信號受到的大、小尺度衰落越嚴重,即距離RX越近,干擾信號功率影響越大,因此,干擾來波功率在三維空間距離上不服從均勻分布[9],假設其服從以RX為中心的高斯分布[10].
(2) 在實際通信中,水平和豎直方向的干擾者(或干擾散射體)分布是不同的,一般來說,仰角越低,干擾者(或干擾散射體)越多,影響越大,因此,高斯分布的標準差需要在水平和豎直方向分別控制.
(3) 由于大規模網絡中節點多且密度高,因此,假設干擾來波數目趨于無窮.
(4) 假設各個干擾衰落信號服從瑞利分布或萊斯分布,由文獻[8, 11]可知,多個瑞利分布或萊斯分布的和分布可近似于一個Nakagami-m分布[12],因此,假設總干擾信號服從Nakagami-m分布.
1.2 干擾功率角度譜密度
假設干擾來波功率在三維空間S中服從高斯分布,其表達式為
(1)

通過雅可比式,將式 (1) 的笛卡爾直角坐標系轉換為球坐標系[13],即
(2)
式 (2)為(r,α,β)的聯合分布,若對r進行積分,則可得(α,β)的聯合分布,即干擾功率角度譜密度,即
(3)
由式(3)可得干擾功率方位角邊緣分布和俯仰角邊緣分布分別為
則干擾水平方向和豎直方向分布是相互獨立的,即pG(α,β)=pG(α)pG(β).
又因為干擾功率俯仰角邊緣分布積分為1,即
(4)

2 干擾空間統計特性
2.1 非規范復球諧系數和三維成型因子

(5)

(6)
2.2 衰落率方差
由于平穩過程的導數均值為零,因此,均方導數即為度量干擾衰落速率的最簡單統計量,而平穩過程的均方導數為變化率的方差,即衰落率方差,可表示為[6]
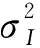
2.3 空間相關函數和相關距離
廣義平穩過程信號包絡r的空間相關函數可由麥克勞林級數表示[14],即
其中,rc為空間距離,Vm(r)為Nakagami-m分布的方差. 而空間相關函數又可近似為指數函數及其麥克勞林級數[5],即
(9)
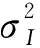
(10)
其中,Γ(·)為Gamma函數,m為Nakagami-m分布的形狀因子. 若定義相關函數為 exp(-1) 時的rc為相關距離Dc,則Dc(α,β)= {2PT[mΓ2(m)- Γ2(m+ 1/2)]}1/2/ [m1/2Γ(m)σI(α,β)].
3 仿真分析
下面主要仿真分析三維空間角度對干擾功率角度譜密度函數和關鍵空間統計特性的影響.針對常見的 2.4 GHz 頻段(即λ= 0.125 m) 通信,為便于分析,將平均接收干擾功率設置為PT=1. 在實際通信中(如市區車車通信),有效干擾者的豎直高度有限,高斯豎直方向標準差設置為σβ= 5 m,即有效干擾者最大高度為 15 m. 通過調整形狀因子m的值,Nakagami-m分布能夠模擬嚴重、適中、輕微到無衰落的信號衰落場景,這里假設干擾信號衰落適中,形狀因子設置為m=2.
3.1 干擾功率角度譜密度
圖2展示了不同高斯水平方向標準差σα和三維均勻干擾空間分布下,俯仰角對干擾功率角度譜密度的影響.在實際通信中,有效干擾者的水平距離可能較遠,因此,圖2考慮了不同σα帶來的影響. 式 (3) 中,俯仰角的單位為弧度,為便于描述,圖2中俯仰角的單位采用度. 若干擾來波功率在半球體中服從以RX為中心的均勻分布,按1.2節方法,此時的干擾功率角度譜密度可計算為 cosβ/ (2π). 由圖2可知,σα越大,干擾功率越集中于更小的仰角范圍,然而σα≥ 400 m 時,各干擾功率角度譜密度曲線趨于重合,這說明由于較大的路損和遮擋,水平距離 3σα≥ 1 200 m 之外的干擾影響已經很小; 在不同σα下,各干擾功率角度譜密度曲線隨著仰角的增大而急劇降低,在仰角為15°時,各干擾功率角度譜密度曲線幾乎降低到零; 在三維均勻干擾空間分布場景下,干擾功率角度譜密度曲線隨著俯仰角增大而極為緩慢的降低,不能很好地表征實際通信中豎直方向有效干擾者少、影響小的規律. 以上干擾空間選擇特性可為智能天線和波束賦形技術的設計提供參考,使天線和波束避開主要干擾以提高系統性能.

圖2 干擾功率角度譜密度圖3 均方根規范化衰落率方差
3.2 三維成型因子和衰落率方差
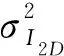
3.3 空間相關函數和相關距離
圖4展示了高斯水平方向標準差σα=400 m時,不同空間間隔距離和俯仰角對空間相關函數的影響. 由圖4可知,間隔距離和俯仰角對空間相關函數都有決定性影響: 在 0°~ 60°俯仰角范圍內,間隔距離的影響占主導地位,且間隔距離rc≥ 0.5λ時,空間相關函數趨近于0; 在 60°~ 90°俯仰角范圍內,俯仰角的影響占主導地位,且俯仰角趨近于90°時,即使間隔距離rc=λ,空間相關函數仍然較大. 圖5展示了高斯水平方向標準差σα= 400 m時,不同俯仰角對相關距離的影響. 同樣,俯仰角對相關距離影響很大,尤其是俯仰角趨近于90°時. 空間相關函數和相關距離是度量信號空間選擇特性的重要指標,其可指導多天線陣列間隔的優化設計.由圖4和圖5可知,多天線陣列陣元間的間隔設置應隨仰角的變化而變化,即為減少干擾相關性的影響,低仰角時需較小的間隔距離,高仰角時需大的間隔距離.綜合圖2~圖5可知,仰角為15°時,干擾功率角度譜密度幾乎降低到零,均方根規范化衰落率方差較大,空間相關性和相關距離也較小,因此,15°仰角也是合適的天線陣列朝向.

圖4 空間相關函數圖5 相關距離
4 結 束 語
針對車聯網、無線傳感器網絡和密集部署網絡等干擾受限的大規模網絡,提出了一個三維高斯干擾空間分布模型,推導出了干擾功率角度譜密度函數和關鍵空間統計特性的閉合表達式,并仿真分析了三維空間角度對干擾功率角度譜密度函數和關鍵空間統計特性的影響. 仿真分析表明,俯仰角是網絡干擾空間選擇特性的決定性影響因素,其中15°仰角處干擾功率角度譜密度幾乎為零,均方根規范化衰落率方差較大,空間相關性和相關距離也較小,這一特性可用于三維智能天線和波束賦形技術的設計和評估.

