基于MATLAB實現的連續信號取樣過程的教學實踐

李燦蘋，劉大召，張瑩

（1.廣東海洋大學電子與信息工程學院，湛江524088；2.廣東海洋大學數學與計算機學院，湛江524088）

0 引言

《信號與系統》是信息技術類專業本科生的一門重要的專業基礎課程，該課程以高等數學、工程數學、電路分析等課程為基礎，是后繼的數字信號處理、通信原理、數字圖像處理等專業課程的先修課程[1,2]，在教學環節上起到承上啟下的作用。通過該課程的學習，可以讓學生掌握信號與系統的基本理論和方法，提高學生運用信號和系統的有關知識去分析和解決問題的能力[3]。

在信號與系統中，連續信號是連續系統中輸入輸出的信號，也是離散信號的主要來源。為了對有用信號進行有效的傳輸和處理，工程上常常首先對連續時間信號轉換為相應的離散信號（或數字信號），進行加工和處理，然后再將處理后的離散信號轉換為連續時間信號[4]。而取樣定理為連續信號與離散時間信號的相互轉換提供了理論依據[4]。

本文從取樣定理出發，針對非帶限信號的取樣問題，以方波為例，通過MATLAB展示了信號的取樣過程，將抽象的理論進行了可視化圖形演示，從而可以加深學生對取樣定理的理解和掌握，激發學生的學習興趣，提高教學質量。

1 取樣定理

若f（t）為帶寬有限的連續信號，其頻譜的最高頻率為fm，則以取樣間隔m的取樣信號fs（t）將包含原信號f（t）的全部信息，因而可利用fs（t）完全恢復出原信號[5]。

因此，信號f（t）取樣后不丟失信息的兩個條件[5]：一是f（t）的帶寬應有限，即頻譜在f>fm時為零；二是取

實際上，信號的取樣過程是完成輸入信號f（t）與取樣脈沖相乘的運算。當取樣脈沖為理想的沖激序列δT（t）時，則取樣信號可表示為：

由于：

其頻譜為：

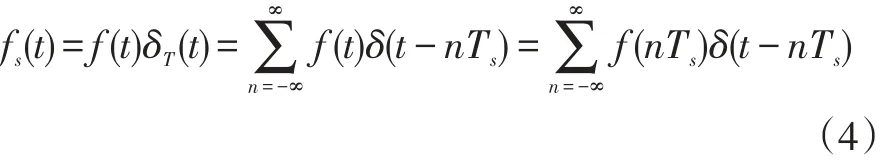
取樣信號fs（t）的頻譜Fs（w）為：

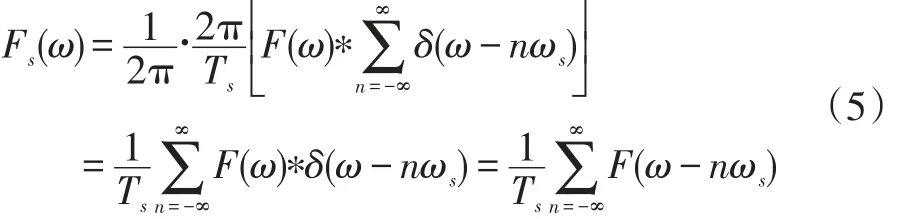
由公式（5）可以看出，取樣信號頻譜Fs（w）是連續信號頻譜F（w）的周期延拓，每隔一個取樣頻率ωs，重復出現一次[4]。對于滿足取樣定理要求的取樣信號，其頻譜只是周期重現且不會產生混疊，能恢復出原信號。但對于非帶限的連續信號，取樣后其頻譜會產生混疊，主周期內的頻譜形狀將發生失真，較難恢復出原信號。

2 方波的取樣

根據取樣定理，對非帶限信號的取樣，為了防止頻譜混疊，在取樣前須加前置低通濾波器，用于濾掉截止頻率以上的信號，如圖1[5]所示。

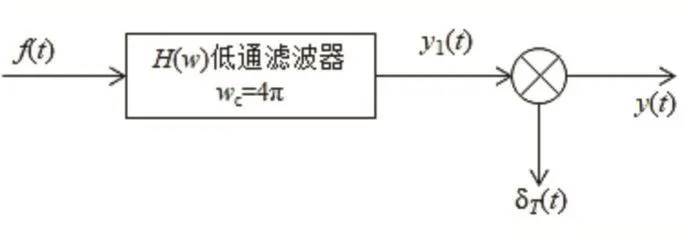
圖1 非帶限信號取樣過程

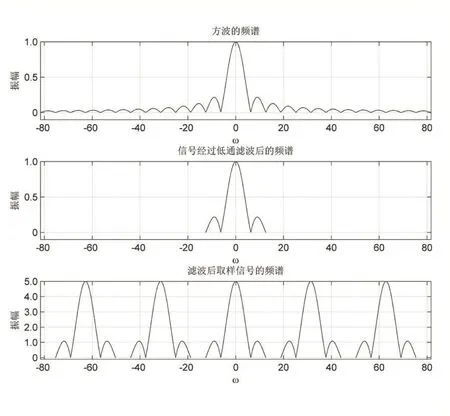
以方波信號為例，實現圖1的取樣過程。輸入信號如圖2（a），其中 f(t)=1，(0

圖2 取樣過程中的信號及濾波器

為了對比加前置低通濾波器前后取樣信號的頻譜，先通過MATLAB實現圖2（a）方波信號的頻譜和直接取樣后的頻譜，程序[5]如下：

clear all

syms t w f;

f=1.0*exp（-j*w*t）;

F=int（f,t,0,1）;

F=simplify（F）;F

subplot（2,1,1）,

low=-26*pi;high=-low;

ezplot（abs（F）,[low:0.01:high]）;grid on

axis（[low high-0.1 1.0]）;xlabel（'omega'）;ylabel（'振幅'）;

title（'方波的頻譜'）;

subplot（2,1,2）,

Ts=0.2;

w0=（2*pi）/Ts;

for k=-2:2

ft=f*exp（-j*w0*k*t）;

FT=int（ft,t,0,1）;

ezplot（（1/Ts）*abs（FT）,[（-16*pi-k*w0）:0.01:（16*pik*w0）]）;

hold on

end

axis（[low high-0.1 5.1]）;xlabel（'omega'）;ylabel（'振幅'）;

grid on

title（'信號直接取樣后的頻譜'）;

程序運行結果如圖3所示。

圖3 方波信號的頻譜及直接取樣后的頻譜

從圖3可以看出，方波信號的頻譜（圖3a）為Sa信號形狀，頻帶范圍較寬，以取樣周期Ts=2s進行取樣后信號的頻譜（圖3b）是對原信號頻譜（圖3a）進行了周期延拓，并發生了混疊，這將影響原信號的恢復。

為了防止取樣信號頻譜發生混疊，在取樣前加前置低通濾波器（圖2b），濾掉截止頻率（wc=4π）以外的頻率成分。通過MATLAB實現圖2（a）方波信號的頻譜、濾波后的頻譜及濾波后取樣信號的頻譜，程序[5]如下：

clear all

syms t w f;

f=1.0*exp（-j*w*t）;

F=int（f,t,0,1）;

F=simplify（F）;F

subplot（3,1,1）,

low=-26*pi;high=-low;

ezplot（abs（F）,[low:0.01:high]）;grid on

axis（[low high-0.1 1.0]）;xlabel（'omega'）;ylabel（'振幅'）;

title（'方波的頻譜'）;

subplot（3,1,2）,

ezplot（abs（F）,[-4*pi:0.01:4*pi]）;grid on

axis（[low high-0.1 1.0]）;xlabel（'omega'）;ylabel（'振幅'）;

title（'信號經過低通濾波后的頻譜'）;

subplot（3,1,3）,

Ts=0.2;

w0=（2*pi）/Ts;

for k=-2:2

ft=f*exp（-j*w0*k*t）;

FT=int（ft,t,0,1）;

ezplot（（1/Ts）*abs（FT）,[（-4*pi-k*w0）:0.01:（4*pik*w0）]）;

hold on

end

axis（[low high-0.1 5.0]）;xlabel（'omega'）;ylabel（'振幅'）;

grid on

title（'濾波后取樣信號的頻譜'）;

程序運行結果如圖4所示。

從圖4中可以看出，方波信號頻譜（圖4a）經過截止頻率為4π的低通濾波器濾波后的頻譜（圖4b）帶寬變窄，對濾波后的信號以取樣周期Ts=2s進行取樣，其頻譜（圖4c）同樣也發生了周期延拓，但并不混疊，所以可以恢復出原信號。

3 課堂教學效果

將以上內容應用到課堂教學中，第1次課首先講述取樣定理內容，理想取樣公式；然后引入圖1所示非帶限信號的取樣過程，給出圖2所示已知條件；最后要求學生通過MATLAB程序完成此取樣過程。

圖4 方波信號的頻譜及其低通濾波后和取樣后的頻譜

第2次課查看學生完成情況，再講解以上兩段程序，并演示程序運行結果。通過圖3和圖4講解非帶限信號的取樣過程，對比分析加前置低通濾波器前后取樣信號頻譜的變化，由此強調取樣定理的重要性。圖形化演示教學進一步加深了學生對取樣定理的理解和掌握，同時，也加強了學生MATLAB編程能力的鍛煉。

4 結語

本文首先論述了信號與系統課程的重要性，然后以取樣定理和理想取樣理論為依據，針對非帶限信號的取樣問題，以方波為例，利用MATLAB實現了方波信號的頻譜、直接取樣后的頻譜、加前置低通濾波器后信號的頻譜。將抽象的理論進行了可視化圖形演示，更加直觀地對比了加前置低通濾波器前后取樣信號的頻譜特點，從而加深了學生對取樣定理的理解和掌握，激發了學生的學習興趣，收到了良好的教學效果。