車頭長度對高速列車氣動特性與聲場特性影響的數值分析及降噪研究

劉曉日，羅江澤，趙 哲，黎 蘇，李 揚

(河北工業大學 能源與環境工程學院，天津 300401)

隨著社會的發展，高速列車越來越多地出現在人們的生活中，因其高速特性，乘坐高鐵出行極大地縮短了人們的乘車時間。但諸多因素阻礙了高速列車的進一步發展，最突出的問題便是其高速行駛時巨大的行車阻力對電力資源極大的需求以及噪聲對人們正常生活的影響，因此降低高速列車的行車阻力和噪聲近年來成為人們研究的熱點[1]。列車的氣動阻力與速度的平方成正比，隨著列車速度的提高，氣動阻力在總阻力中所占比例逐漸增加，列車速度超過一定值時，氣動阻力成為高速列車的主要阻力[2]。通過高速列車氣動優化設計能夠有效降低氣動阻力、提高高速列車的氣動性能[3]。對于時速為250～300 km·h-1的高速列車來說，總阻力的75%～80%起因于外部氣動阻力[4]。高速列車的頭部對周圍空氣流場具有決定性的影響，從列車頭部著手改善車體外形是研究的重點[5]。當列車的運行速度達到300 km·h-1，列車運行所產生的氣動噪聲將會超過輪軌噪聲，成為高速列車的主要噪聲[6]。文獻[4]將理論分析、實驗研究、數值模擬相結合，對不同型號的高速列車各種行駛環境下的空氣動力特性以及噪聲源進行分析。文獻[7]建立3種縱向剖面線和3種水平剖面線組合下的9種高速列車頭型，研究了頭部控制線形狀對高速列車氣動噪聲的影響。文獻[8]通過對鐵路車輛噪聲源機理和噪聲源位置的分析，提出了降低噪聲的方法。文獻[9]研究了不同速度下高速列車周圍流場的變化，得出氣動噪聲在很寬的頻帶內存在，是1種寬頻噪聲；控制列車運行過程中產生的脈動壓力，能夠減少氣動噪聲。文獻[10]對4種不同頭部外形高速列車的氣動性能進行風洞試驗研究，實驗表明車頭外形越細長，對減阻越有利。文獻[11]對鼻尖高度、排障器前端伸縮量、轉向架區域擋板傾角等關鍵設計變量進行了優化設計以及與氣動阻力和氣動噪聲的相關性分析，在此基礎上提出了綜合性能較佳的新頭型氣動外形。文獻[12]對高速列車的流線型頭型進行多目標優化設計，優化后的列車氣動阻力減小了4.15%。

本文應用等比例同距離方法對高速列車頭部進行模型構建，將車頭長度設置成模型變化的唯一參數，從理論上保證了模型的相似性。寬頻噪聲模型采用的RNG k-epsilon模型做定常計算，FW-H聲學模型采用大渦模擬(LES)模型進行瞬態計算，同時對高速列車的表面壓力、阻力、升力、氣動噪聲偶極子聲源、遠場氣動噪聲特性進行分析，并總結出這些參數隨車頭長度的變化規律，將同一速度、不同高速列車模型附近的脈動壓力分布規律和遠聲場信息進行對比分析。

1 計算模型

1.1 理論基礎

寬頻噪聲模型采用的RNG k-epsilon模型做定常計算，FW-H聲學模型采用大渦模擬(LES)模型進行瞬態計算。

RNG k-epsilon方程為

Gk+Gb-ρε-YM+Sk

(1)

(2)

式中：GK表示由于平均速度梯度而產生的湍流動能；Gb表示由于浮力而產生的湍流動能；YM代表在可壓縮湍流中波動膨脹的貢獻對總耗散率的貢獻；αK和αε分別表示k和ε的逆普朗得系數；Sk和Sε為自定義有源項。

大渦模擬(LES)控制方程為

(3)

(4)

對于高速列車氣動噪聲的研究，常采用萊特希爾(Lighthill)的理論,用單極子、偶極子和4極子聲源來代表氣動噪聲源。單極子和偶極子聲源分布于物體的表面，4極子聲源分布于物體周圍的流體空間。當分析問題時，因為將運動的固體視為剛體，所以忽略了單極子聲源。Lighthill總結了流場中4極子和偶極子所產生的聲強比為ΙQ/Ιd∝(Uo/ao)2H(R)，其中的Uo為物體運動的速度，ao為當地聲速。由此可得，氣動噪聲中4極子聲源與偶極子聲源強度之比正比于馬赫數的平方。本文中設定高鐵的運動速度約為0.285馬赫，屬于低馬赫運動，其4極子源噪聲強度遠小于偶極子源，故4極子源也可忽略不計。流體對固體的脈動壓力不能產生流體中的聲波而是固體中的振動波，只有固體對流體的起伏力能導致聲波的產生，高速列車的噪聲源可簡化成偶極子聲源。在做這種簡化時聲源的尺寸應遠小于其向外輻射聲波的波長，而高速列車的長度大，所以在高速列車的表面分布有無窮多個偶極子聲源。因此，了解高速列車表面的氣動偶極子分布規律，是降低高速列車氣動噪聲的基礎。

不同聲源的聲輻射場是不同的，而運動聲源的聲輻射場又不同于靜止聲源的聲輻射場，流場中勻速運動固壁表面所誘發的氣動偶極子聲源的空間聲輻射指向特性與諸多因素相關，譬如物體的運動速度、脈動壓力的頻率、偶極子的運動方向和觀察者方向的夾角等。在實際的監測過程中還需考慮運動聲源的多普勒效應，隨著聲源與接受者之間距離的縮短，收到的聲波頻率較高。綜上所述，獲得高速列車周圍的聲場信息是非常困難的[13]，需要設置有限個監測點，通過這些點的變化情況來推測整個聲場的變化[14]。

1.2 幾何模型

在改變車頭長度的同時車頭曲面也會發生變化，保證不同長度的車頭曲面的相似性是研究問題的基礎。如圖1所示，選定1條主軸線，主軸線起始于水平樣條控制線和橫向樣條控制線的交點，沿水平方向終止于車身控制線所在的平面。主軸線的長度即表示車頭的長度，使得生成車頭曲面的控制線和主軸線通過若干條距離控制線(圖中未標記線條均為距離控制線)相關聯，即可在改變主軸線的同時使得頭型控制線改變。按上述方法應用進行三維建模，在車頭曲面生成過程中車頭形狀僅由水平、橫向樣條控制線和車身形狀控制線決定。車頭的長度由主軸線的長度確定，在生成5～13 m車頭長度過程中僅通過改變主軸線的長度，便可得到不同的模型形狀。車尾和車頭長度是相同的。

圖1 高速列車簡化模型形狀控制線

高速列車運行時通常為6～8節車廂，每節車廂的長度在24～27 m范圍內，總長度超過200 m。中國還開始試驗運行世界首列加長版16輛編組列車，總長度將超過400 m。由于高速列車外形較為復雜，考慮到計算規模，有必要對其外形進行簡化。列車行駛時，氣流在中間車的結構層趨于穩定，在各個中間車脈動壓力情況較為一致，因此本文建立了由3節車廂組成的列車模型，包括頭車、尾車和1節中間車。由于車頭長度為變量，本文的列車模型長度范圍為70～86 m。圖2為高速列車簡化模型，圖3為5個長度不同的列車模型頭部對比。

圖2 高速列車簡化模型

圖3 車頭長度分別為5，7，9，11，13 m時模型頭部側視圖

1.3 網格劃分

在列車周圍2 m的空間區域采用非結構網格,流動區域的其他部分采用結構化網格。結構化網格比非結構化具有網格生成的速度快、質量好、網格數量少的特點，并且在結構化網格的生成過程中通過控制邊線的節點數以及節點的分布規律，使得從高速列車由內到外網格由密變疏，以更加準確地捕捉高速列車周圍的小尺度渦。因此，針對高速列車空氣動力學和聲場模擬過程中存在的巨大空間區域，結構化網格的應用可以極大方便地解決由非結構網格導致的數值模擬計算精度差問題。本文中不同模型的網格數量因不同車頭長度的改變而不同，5 m時總網格數量約為923萬個，13 m時網格數量約為1 275萬個。流場域網格劃分如圖4所示。

圖4 流場域網格劃分

1.4 網格無關性驗證

在簡化模型2 m區域之內采用了非結構化網格，其他區域采用結構化網格。為減少由于網格帶來的計算誤差，保證數值模擬的精準度，取車頭長度為9 m的模型，結構化網格使用4種不同數量的網格，不同網格方案的不同主要體現在非結構網格數量的差異，按照非結構網格數量從小到大分別將4種方案命名為Ⅰ，Ⅱ，Ⅲ，Ⅳ。以k-epsilon穩態流場結果下求得的阻力作為評估網格質量的指標，由表1可得。隨著網格數量的增加，所得出的阻力也逐漸增大。通過相鄰方案的阻力相對變化率可以看出由模型Ⅲ到模型Ⅳ，阻力變化率僅為1.0%，遠小于模型Ⅱ及Ⅲ對應的5.5%和5.6%。考慮到阻力變化率和節省計算機資源，本文采用第Ⅲ種網格方案。

表1 不同網格方案對比

1.5 計算區域及邊界條件

如圖5所示，高速列車正前方來流方向截面為入口邊界，設置為速度入口條件，速度為350 km·h-1。正后方截面為出口邊界，設置為壓力出口條件。高速列車的左側、右側和正上方截面設置為對稱邊界，列車表面設置為無滑移壁面邊界。為了模擬地面效應，地面設置為滑移地面，其滑移速度為列車運行速度。列車與地面之間的距離為0.376 m。圖中L，W和H分別代表高速列車簡化模型的長寬高[15]，整個計算域的長度為4L，寬度為24W，高為10H。

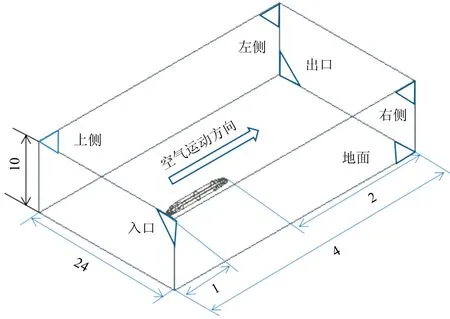
圖5 計算區域尺寸(m)

2 動力特性結果

2.1 壓力

由圖6可知，當高速列車車頭長度為5 m，速度為350 km·h-1時，車尖壓力最大處達到5 665 N。隨后沿車頭壓力逐漸降低，一直降低到負壓區，在車頭與車身連接處達到最小值-4 405 N，再沿車身方向壓力值先小幅度上升，隨后維持在1個固定值保持不變。在達到車尾與車身連接過渡區域時壓力再次降低，達到與車頭和車身連接過渡區域相同的負壓值，并且負壓區出現的區域和負壓值沿車身中間面呈現對稱趨勢。到車尾部，壓力值逐漸增大直至車尾末達到1 158 N。

圖6 車頭長度為5 m時列車表面壓強分布云圖

對比5～13 m不同車頭長度的高速列車表面壓力分布均有相同的壓力分布趨勢，且最大壓力值保持在5 560～5 750 N之間(因計算誤差有小幅度波動)，但最小壓力值呈現逐漸增大的趨勢。若曲線擬合方程為Y=-9 702.571 43+1 337.428 57x-52.857 14x2，則R2=0.988 6。擬合曲線如圖7所示。

2.2 阻力和升力

由圖8可知隨著車頭長度的增加，氣流的分離減弱，壓差阻力呈現減小趨勢，變化趨勢趨向平緩，由5 m時的2 649.37 N減小至13 m時的500.46 N。摩擦阻力呈線性上升趨勢，由5 m時的6 457.21 N增長到13 m時7 327.75 N。在壓差阻力和黏性阻力的綜合作用下總阻力呈現出先減小后增大的趨勢。由此可得，通過增加車頭長度來減少阻力會有1個極限值，過大的車頭長度反而會使得阻力增加。

圖7 最小靜壓力隨車頭長度的變化

氣動阻力擬合曲線方程：

Y=6 424.59-963.64x+39.36x2，

R2=0.979

摩擦阻力曲線擬合方程：

Y=5 923.95+107.79x，R2=0.998

總阻力曲線擬合方程：

Y=15 462-2 037.88x+179.02x2-5.19x3，R2=0.988

圖8 阻力隨車頭長度變化曲線

由圖9可知高速列車車頭長度為5 m，是升力的絕對值，最大為598.34 N。將車頭長度為7～15m的列車模型升力值取絕對值之后，均小于200 N，并無明顯差異。這表明車頭長度過小將導致升力的絕對值過大，車頭長度大于等于7 m之后升力的絕對值趨于穩定。負的升力值讓列車在輪軌上平穩行駛，但如果負升力值過大，將產生過大的摩擦阻力，為克服摩擦阻力將消耗過多的電力資源。

圖9 升力隨車頭長度變化趨勢

3 氣動噪聲

3.1 聲功率級分布特性

對比5～13 m不同長度的高速列車簡化模型表面偶極子聲功率級分布云圖可知，列車表面的最大聲功率級出現在車頭部位，車身部位的聲功率級比車頭部位進一步減小，并且保持一定，不隨車身變化。車身與車尾連接處聲功率級較大，直至車尾盡頭聲功率級處于比較低的水平。隨著車頭長度的增加，車頭部位最大聲功率級呈現出減小趨勢，兩者的關系接近線性，如圖11所示。若擬合函數定義為y=-0.955x+106.33，則R2=0.97。而車身部分并無差別，車身與車尾連接處聲功率級呈現出減小趨勢，尾車的聲功率級分布更加均勻。

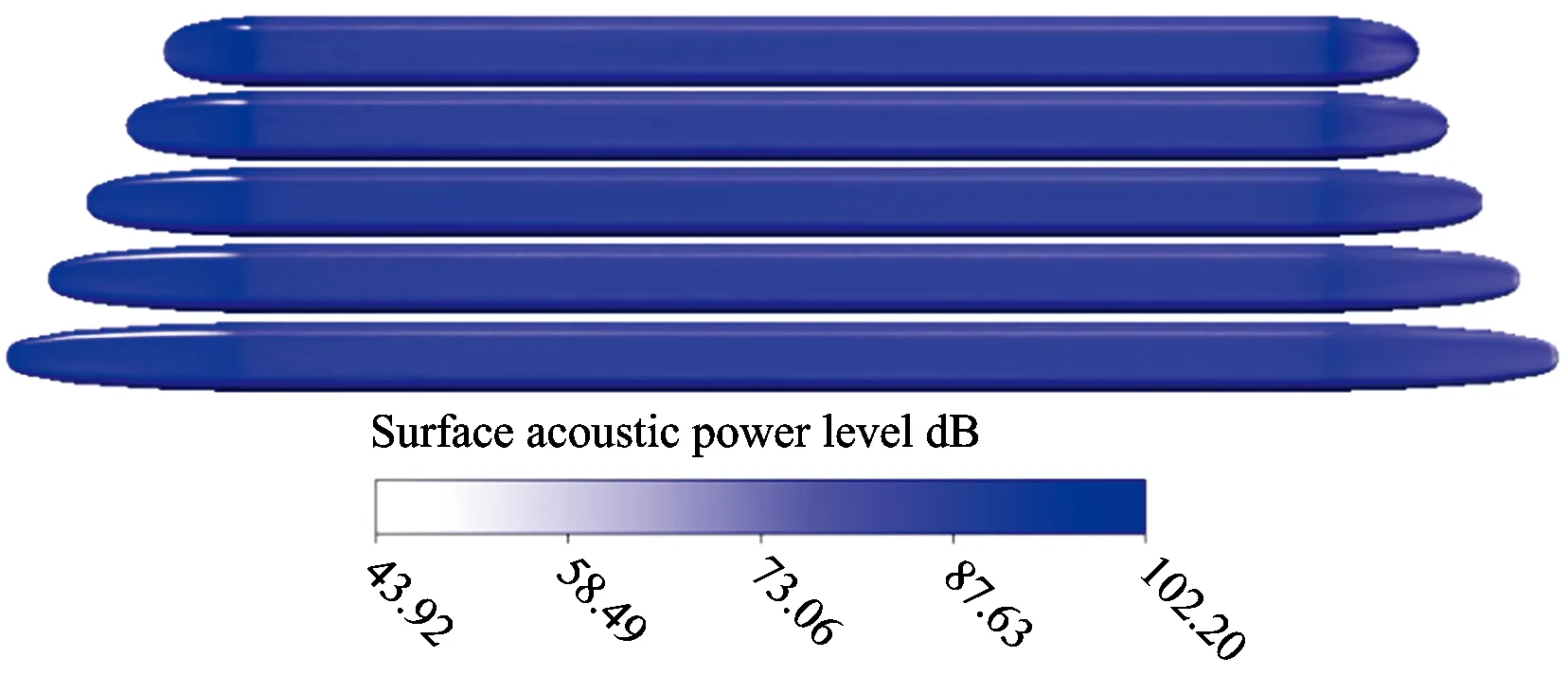
圖10 5～13 m長度車頭的列車表面聲功率級分布對比云圖

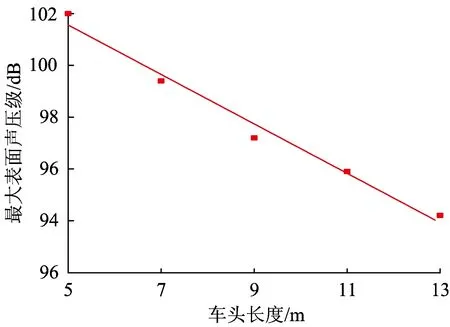
圖11 最大聲功率級隨車頭長度變化趨勢

3.2 遠場氣動特性

根據數值模擬所得到的聲場結果，在距軌道25 m遠、距地面高3.5 m的區域，布置11個監測點，列車行駛方向依次為1～11監測點，如圖12所示。監測點3和9分別對應車身段的起點和終點，監測點2和點10分別對應列車的起點和終點，相鄰監測點之間的距離為10 m。

圖12 遠場氣動噪聲數值仿真監測點分布示意圖

從圖13可以看出，隨著車頭長度的增加，點1和點11的聲壓級呈現出減少趨勢。點1聲壓級減少趨勢較為緩和，總共下降3.67 dB，而車頭長度從5 m到7 m點11聲壓級下降較大，達到7.06 dB，隨后大致保持不變；點2和點10聲壓級并無明顯變化，和車身部位相對應的監測點總體上呈現出增大趨勢，由9 m至11 m聲壓級增大幅度最大。由于高速列車模型為簡化模型，并沒有包括輪轂、轉向架和受電弓等復雜的結構，因此仿真得到的聲壓級較小。

圖13 各個數值仿真監測點聲壓級隨車頭變化情況

針對和車身部位相對應的監測點3—9呈現出的增大趨勢，為更好地對比其差別，將車頭長度一定時的這7個監測點求和之后取平均值，如圖14所示。由圖可見，隨著車頭長度的增加，車身部位所對應監測的平均聲壓級呈現出非線性的增加趨勢，車頭長度在5～13 m范圍內，聲壓級增長幅度呈增大趨勢，若擬合方程為Y=75.94-0.95x+0.087x2，則R2=0.953 5。

由7個聲壓級監測點可以看出高速列車遠場聲壓級的大致規律，車身對應的監測點聲壓級大致相等，沿兩端方向聲壓級開始逐漸降低，沿頭車方向比沿尾車方向聲壓級降低緩慢。一般認為，高速列車氣動噪聲的生成和其表面的脈動壓力有關，現對其進行分析。

圖14 車身部位所對應數值仿真監測點的平均聲壓級

圖15中(a)—(e)分別列出了5～13 m高速列車中軸線的縱向和水平橫截面動壓力云圖。由圖可知，車體附近的脈動壓力值較大，且沿著中軸線成對稱分布，脈動壓力的最大值出現在車身與車頭、車尾的連接處，此處曲面的曲率變化大，旋渦脫落較大，氣流擾動較為劇烈。隨著車頭長度的增加，連接處的曲面曲率值減小，最大脈動壓力值呈現出減小趨勢。脈動壓力影響的范圍也出現了變化，沿橫向的影響范圍減少，但隨著車頭長度的增加，較大動壓在縱向的影響區域變大。由此可知，高速列車附近的脈動壓力值的大小和分布狀況決定了監測點的聲壓級，脈動壓力在縱向上的增加會使得車身所對應的監測點聲壓級迅速上升，可知通過控制高速列車車頭的長度，不僅可影響氣動噪聲的影響范圍，還可減少遠場監測點的聲壓級。

圖15 高速列車周邊脈動壓力隨車頭長度變化對比云圖

車頭長度為9 m，速度為350 km·h-1時數值仿真監測點6的頻譜圖如圖16所示。由(a)可知遠場監測點的聲壓級在很寬的頻率內存在，低于400 Hz時聲壓級逐步增大，400～1 600 Hz時聲壓級呈現出由大變小的趨勢，1 600～5 000 Hz范圍內聲壓級值較為穩定。為了使聲音的客觀物理量和人耳聽覺感受近似取得一致，人們一般對測量得到的聲音進行A計權處理，將其進行A計權之后噪聲低頻成分進行衰減，所得結果如圖(b)所示。低頻所占的比重降低，從低頻到高頻聲壓級逐漸升高，當頻率到達1 000 Hz時所對應的聲壓級最大為65.5 dB，1 000～5 000 Hz時A計權聲壓級緩慢減小。

圖16 車頭長度為9 m時數值仿真監測點6的頻譜圖

將車頭長度分別為5和13 m時遠場監測點6的頻譜圖相對比可得聲壓級的增大在一個很寬的頻率范圍內存在，如圖17所示。在低于300 Hz時13 m所對應的聲壓級有所降低，在300～700 Hz范圍內兩者基本持平，在700～5 000 Hz范圍內13 m所對應的聲壓級大于5 m時，在1 400～2 250 Hz范圍內13 m所對應的聲壓級超出5 m的較多。

圖17 車頭長度分別為5和13 m時監測點6的頻譜對比

在車頭長度為9 m，速度為350 km·h-1時模型車頭鼻尖處設置脈動壓力監測點，在得到充分震蕩的脈動壓力時程曲線以后，進行傅里葉變換得到監測點的聲壓頻譜圖，脈動壓力時程曲線圖均呈現出類似圖18所示的波動，脈動壓力的峰值有所差異，所得結果和圖15中相同。頻譜圖均呈現出圖19的趨勢，各點的氣動噪聲在很寬的頻譜內存在，無明顯主頻率，隨著頻率的增大，幅值逐漸減小。

圖18 車頭長度為5 m時數值仿真監測點1的脈動壓力時程曲線

為得到本模型下最佳的車頭長度，根據數值模擬計算得到的阻力變化規律(圖8)和遠場噪聲監測點的平均聲壓級(圖14)，表2列出了隨著車頭長度的變化阻力相對降低率和聲壓級的相對增長率。從表2中可以看出，車頭長度由9 m到11 m阻力相對降低率為最低1.4%,而聲壓級的增長率達到最大為4.7%，由此可得在此模型下最佳的車頭長度為9 m。

圖19 車頭長度為5 m時數值仿真監測點1聲壓級頻譜

表2 阻力和聲壓級隨車頭長度變化規律對比

4 結 論

(1)高速列車的阻力隨著車頭長度的增加呈現出先減小后增大的趨勢，因為壓差阻力隨著車頭長度的減少是有限的，而黏性阻力與車頭長度成線性關系。高速列車的升力隨著車頭長度的增加亦呈現出先減小后增大的趨勢。

(2)隨著車頭長度的增加，車頭部位最大聲功率級呈現出減小趨勢，關系接近線性，而車身部分并無差別，車身與車尾連接處聲功率級呈現出減小趨勢，尾車的聲功率級分布更加均勻。

(3)數值模擬監測點的平均聲壓級呈現出非線性的增加趨勢，結合阻力的變化趨勢，可得最佳的車頭長度為9 m，在此車頭長度下阻力尚未開始增長，遠場數值模擬監測點的平均聲壓級的增加幅度并不大，即可減小行車阻力同時控制噪聲對環境的污染。

(4)隨著車頭長度的增加，高速列車附近的最大動壓值逐漸減小，在模型表面設置的數值模擬監測點呈現出隨機震蕩，進行傅里葉變換之后，隨著頻率的增大，聲壓級幅值逐漸減小；遠場數值模擬監測點聲壓級的增大，是由于在700～5 000 Hz范圍內聲壓級的增大導致。