基于Hertz接觸力模型的齒輪傳動系統力學分析與仿真

高準， 楊瑞超， 李良， 董紅衛

（西安航天精密機電研究所，西安 710100）

0 引言

RV（RotateVector）減速器是在行星齒輪傳動和擺線針輪傳動基礎上發展而形成的一種新型的兩級封閉差動行星輪系傳動減速裝置，因其具有一系列優點，RV減速器在精密傳動領域得到了廣泛應用。RV減速器的傳動原理包括擺線針輪傳動和行星齒輪傳動兩大部分。RV減速器由于受到結構尺寸的限制，使用了大量具有變位系數的微小齒輪，這極大地增加了齒輪傳動的計算分析難度。

回差是指輸入軸反向轉動時，輸出軸在運動上滯后于輸入軸的現象。回差可以根據其產生的原因而分為三大類：一是單純由于傳動件幾何尺寸、形狀方面的原因所產生的回差[1-2]；二是裝配誤差：部件安裝于箱體內后,因為軸、軸承、箱體等零件的制造、安裝誤差而引入的回差；三是齒輪在運行過程中由于載荷的作用存在彈性形變而產生的回差。前兩種誤差在進行設計時，根據齒輪精度的選擇、齒輪箱的精度設計，可以精確計算行星齒輪的回差，工程上一般將第三種回差稱為彈性回差，需要通過動力學仿真進行計算。RV傳動是由漸開線齒輪行星傳動和擺線針輪行星傳動組成的封閉差動輪系，因此，RV傳動總的回差是由漸開線齒輪行星傳動引起的回差和擺線針輪傳動引起的回差兩部分合成[3-6]。分析行星傳動的回差對于RV傳動總的回差具有重要的意義[7]。

本文基于ANSYS有限元仿真分析軟件在計算機上建立行星齒輪接觸仿真分析模型，將行星傳動的回差結果與有限元仿真計算結果進行比對，證明了基于ANSYS有限元仿真分析軟件計算方法的準確性、經濟性和可靠性。為行星傳動的回差計算提供了一種新的參考。

1 行星齒輪傳動回差分析

1.1 行星齒輪的動力學分析

行星減速器在使用過程中，受力情況復雜，齒輪存在一定的彎曲形變，導致行星減速器的回差計算結果與實際測量結果存在一定的誤差，必須對齒輪等關鍵零件進行計算以建立行星減速器正確的回差傳動計算模型，保證產品的輸出精度滿足指標。

行星齒輪傳動系統中，主要受力的結構件有行星輪、太陽輪、行星架、軸以及軸承[8-11]。本文僅對太陽輪與行星輪進行動力學分析。該型號RV減速器存在3個行星輪，且行星輪載荷均勻，因此本文僅分析其中一個行星輪與中心輪的組合。根據RV減速器工作情況，該型號潤滑良好，可以略去摩擦力和重力的影響。則行星齒輪減速系統的受力分析如圖1所示。

圖1 齒輪受力分析

通過對圖1中的太陽輪a、行星輪c進行力學分析可得上述結構件的圓周力、徑向力等如表1所示。

根據上述計算公式、產品的實際輸入功率和行星齒輪傳動系的實際加工情況可以計算出行星齒輪傳動系的形變量，進而計算出在動態環境下的齒輪形變，建立行星齒輪傳動系的回差計算模型。

表1 行星齒輪受力分析

1.2 動態環境下行星齒輪的回差模型

本節將以某具體型號RV減速器的直齒輪傳動系統為研究對象，計算該型號直齒輪傳動系統在動態環境下的回差模型，該型號中，額定轉速n1=3000 r/min，輸入功率P=300 kW，太陽輪和行星輪輪齒數分別為z1=18，z2=36，齒輪模數m=1 mm，太陽輪和行星輪均使用GCr15加工，密度ρ=7.9 g/cm3，彈性模量E=206 GPa，泊松比μ=0.3。

則電動機的輸出轉矩為[12-13]

式中：P為電動機的輸入功率，kW；n1為電動機的輸入轉速，r/min。

則行星輪施加給太陽輪的圓周力Ftca為

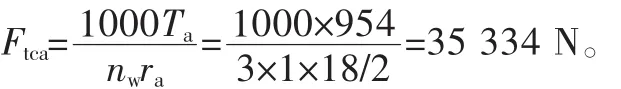
式中：Ta為電動機的輸出轉矩，；nw為行星輪數量；ra為太陽輪的分度圓半徑。

根據相關手冊可得太陽輪和行星輪嚙合過程中，Hertz剛度系數

式中：R1、R2為太陽輪和行星輪接觸處的曲率半徑；h1、h2為材料參數。hi定義為，其中，μi為泊松比；Ei為彈性模量。

最后根據該型號RV減速器各個零件的實際選材情況，計算得到太陽輪和行星輪的接觸剛度系數k=334.8×107N/m。

最終計算得到在減速器嚙合過程中，齒輪的彎曲形變量為

在該型號下，齒輪的彎曲形變量導致回差的變化為

根據上述分析，在行星齒輪傳動過程中，由于接觸力的存在，導致行星傳動系統的回差為4.1′。

1.3 行星齒輪的結構建模及仿真分析

本文利用Pro/E三維設計軟件構造出行星齒輪的簡化結構。將其導入 ANSYS Workbench有限元分析軟件中進行計算，行星傳動系統的有限元模型如圖2所示。

圖2 行星傳動系統的有限元模型

根據實際工況，將小齒輪固定，行星輪之間選用的接觸類型是Frictionless Support[14-15]，根據1.2節計算結果，給大齒輪施加954 N·m的力矩，設置好上述材料、載荷等參數之后計算該工況下，齒輪的形變量，計算結果如圖3所示。

圖3 行星傳動系統的計算結果

從圖3中可以看出，在動態環境下，行星齒輪嚙合過程中，齒輪的形變數值為0.084 mm，與1.2節計算結果相比，差為7.4%，滿足工程中小于10%的要求。

2 結論

本文基于Hertz接觸力模型，建立了行星傳動齒輪的形變計算模型，根據齒輪的形變量計算了其對傳動系統回差的影響。在相同的力學輸入工況下使用有限元仿真分析軟件，對齒輪的形變量進行了仿真分析，通過仿真，證明了使用有限元仿真分析軟件可以較為準確地計算特定載荷下的齒輪的形變量，為研究齒輪的形變計算提供了一定的參考。