小波濾波在光纖慣導抗干擾初始對準中的應用

石利利，張志鑫，吳海仙，吉云飛

（北京航天時代光電科技有限公司，北京100094）

0 引言

初始對準是捷聯慣導系統的關鍵技術之一，初始對準的精度和時間很大程度上決定著武器系統的性能和戰斗力。在工程應用中，由于外界干擾因素的存在，慣導系統不可避免地存在角運動和線運動的干擾，從而難以實現快速對準。文獻［1］詳細推導了基于慣性系的粗對準算法來隔離晃動基座的影響，提高了晃動基座條件下的粗對準精度。但是，該方法只能有效隔離角運動干擾的影響，當線運動干擾較大時，對準結果收斂過程仍振蕩劇烈，對準時間長，對準精度低。為解決此問題，可在對準之前進行預濾波，以減小高頻噪聲對對準性能的影響。

一般情況下，由于噪聲主要分布在高頻部分，通過合理設置截止頻率，采用低通濾波器即可達到消除高頻噪聲的目的。但是，當有用信號和噪聲相互混疊時，低通濾波效果不太理想。而小波濾波具有良好的時頻特性和多尺度分析特性，能夠分離出與噪聲相混疊的有用信息。部分文獻研究了小波濾波在初始對準中的應用。文獻［2］證明了小波濾波可以提高光纖慣導精對準的精度，但對準時間較長。文獻［3］、文獻［4］討論了在基于慣性系粗對準之前先進行小波預濾波對粗對準精度的影響，沒有分析對精對準的影響，且以上文獻都不滿足實時性的要求。基于文獻［5］、文獻［6］提出的實時小波濾波方法，結合慣性系粗對準和Kalman濾波，本文通過車載實驗重點研究小波實時去噪對對準精度和收斂時間的影響。

1 系統實現

傳統的基于慣性系的雙矢量定姿算法可以有效隔離角運動干擾，但是對線運動干擾敏感［7］，當線運動干擾較大時，若采用如圖1所示的傳統初始對準算法，光纖捷聯慣導系統的對準性能仍較差。而本文先通過小波實時濾波算法對慣性儀表輸出數據進行預處理，以減小高頻噪聲對對準性能的影響，然后進行慣性系粗對準和Kalman濾波精對準，系統實現流程如圖2所示。

2 多尺度分析方法——Mallat算法

小波多尺度分析在時域、頻域都有良好的局部化性質，具有 “數學顯微鏡”之稱。利用小波的多分辨率特性對信號進行處理，尺度較大時，頻率分辨率高，適于分析低頻信號；尺度較小時，時間分辨率高，適于分析高頻信號［8］，相當于多個帶寬不同的濾波器對信號進行處理，濾波效果通常優于傳統濾波器，近年來在音頻、圖像、探地雷達和醫學成像與診斷等領域的信號處理中得以應用［9］。應用于小波多尺度分析的常見算法為Mallat塔式分解與重構算法［10］。以2階樣條小波函數ψ（x）為例，算法分為分解和重構兩個過程，如圖3所示。

設其分解的低通和高通離散濾波器分別為H和G，重構的低通和高通離散濾波器分別為h和g（h、g分別是H、G的對偶算子）。其中，C0為原始數據，C′0為經小波濾波處理后的數據；Ci（i＝1， 2，…，n）為低頻系數，表征了信號的概貌信息；Di（i＝1，2，…，n）為各尺度高頻系數，表征了信號的細節信息；“↓2” 代表2取1的 “抽取計算”，“↑2”代表在兩個數據之間的 “插零運算”。重構過程中，各高頻系數需先進行閾值處理，Ti（i＝1，2，…，n）表示各級的閾值大小。

3 小波實時濾波方案設計

小波域閾值濾波由Donoho于1995年首次提出［11］，由3個步驟組成：信號分解、信號去噪和信號重構。為達到理想的去噪效果，需要選擇合適的小波基、分解尺度、閾值函數和閾值。

通常小波閾值降噪都是離線處理，無法滿足慣組實時解算的需求。本文采用帶滑動數據窗的小波濾波算法，并采用邊界值重復的對稱周邊延拓的方法來處理邊界問題，能夠對慣性儀表輸出信號實時降噪。具體實現方式如圖4所示。

設數據窗的寬度為N，先輸出與數據窗等寬的數據量x1～xN。當輸出信號的長度達到窗口寬度時，開始動態獲取N個輸入值按順序組成一維數組，并向右進行對稱周期延拓，然后進行Mallat多尺度分解與重構，最終生成N個新數據x′1～x′N。其中，把x′N作為當前時刻T的濾波輸出，下一時刻T＋1，采樣得到新的原始數據xN＋1，此時先去掉x′1， 并將x′2～x′N依次向左移一個位置， 并將xN＋1補充到x′N空出的位置，組成新的一維數組。然后再對其進行對稱周邊延拓并進行小波濾波，循環執行以上操作，便可以實現對慣性儀表輸出信號的實時降噪。

常用的閾值方法分為硬閾值法和軟閾值法，本文采用軟閾值法進行降噪處理，軟閾值法表示為：

式中，wj，k為第j層小波系數，Tj為第j層小波閾值，小波閾值根據VisuShink閾值選取準則來確定，計算公式為：

式中，σj為各層噪聲信號標準差，N為信號長度。在實際應用中，陀螺儀和加速度計噪聲信號的標準差是未知的，所以在降噪前需要對噪聲水平進行估計。噪聲的標準差可以根據各尺度細節小波系數絕對值的中值來估計［12］，即：

另外，在實際應用中，需要根據信號特性以及合適的準則來選取小波基和分解尺度。設計實驗（具體方法見第4節）得到慣性儀表在晃動基座下的輸出信號，天向陀螺輸出信號的頻譜圖如圖5（a）所示。從頻譜圖中可以看出，信號中混入的噪聲存在于全頻段，發動機振動的頻率主要集中在27Hz附近，在20Hz和53Hz附近有少量分布，走動、晃動的頻率主要集中在1.8Hz和4.3Hz附近。不同方向的陀螺頻譜圖略有不同，但基本吻合。進一步分析各軸加速度計信號的頻譜圖，分析結果與陀螺頻譜圖基本一致。信號采樣頻率為f＝200Hz，采樣頻率和分解尺度共同決定了對應小波系數頻帶的范圍，根據頻譜分析結果，本文選取小波分解尺度為7層， 將頻帶限制到 0.8Hz（f/2/27）。 一般情況下，選擇小波基時希望選擇緊支撐、對稱、正交性好以及消失矩高的母函數，通過比較幾種小波的濾波效果，本文選取dB5小波作為小波基。

4 系統對準實驗及分析

為驗證預濾波效果，用光纖慣導系統在車載怠速條件下進行試驗。試驗總共進行了6次，每次采樣時間為5min，將實測數據在Matlab中模擬實時降噪過程，利用前文所述的降噪方案對其進行預處理，窗口寬度為64。圖5（b）給出了經小波濾波后天向陀螺輸出信號頻譜圖，圖6給出了預濾波前后天向陀螺輸出信號的時域圖。可以看出，除去剛開始小于窗口寬度的輸出值，信號中的高頻噪聲得到有效抑制。

4.1 慣性儀表輸出信號統計特性

比較了晃動基座下6組試驗數據小波預濾波前后慣性儀表輸出信號的統計特性，其中一組數據的比較結果如表1～表4所示。

表1和表3對比了預濾波前后陀螺儀和加速度計的均值，可以看出均值幾乎不變；表2和表4對比了預濾波前后陀螺儀和加速度計的標準差，從結果中可以看出，經小波預濾波后光纖陀螺儀的輸出噪聲降到了濾波前的10%以下，加速度計的輸出噪聲降到了濾波前的5%以下。

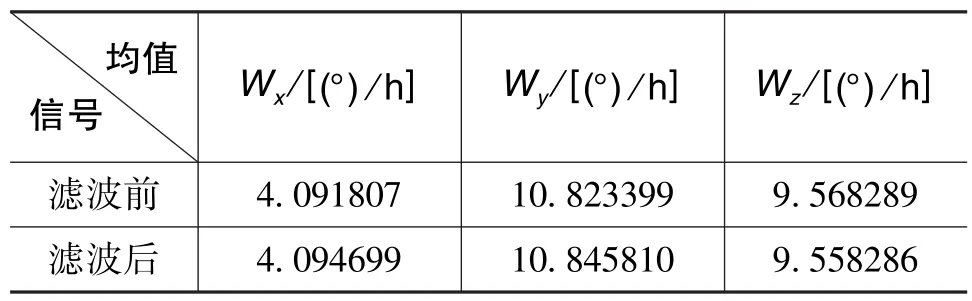
表1 小波預濾波前后陀螺均值Table 1 Mean value of gyro before and after wavelet pre?filtering

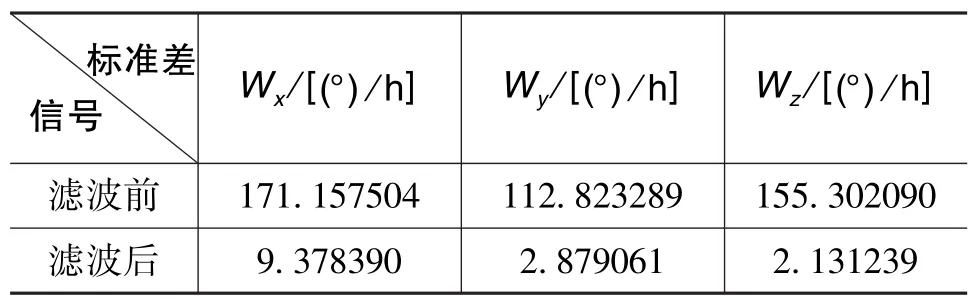
表2 小波預濾波前后陀螺標準差Table 2 Standard deviation of gyro before and after wavelet pre?filtering

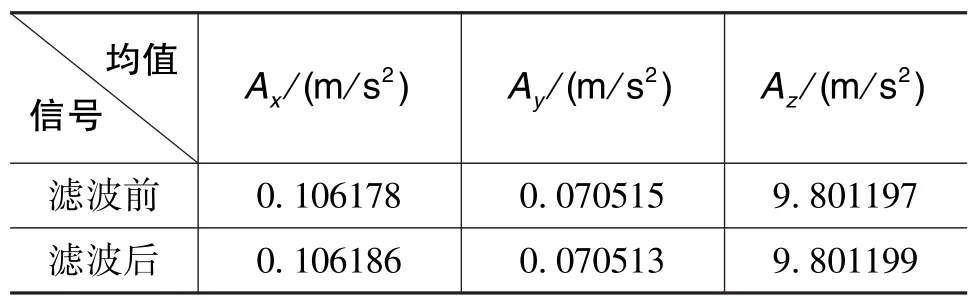
表3 小波預濾波前后加速度計均值Table 3 Mean value of Accelerometer before and after wavelet pre?filtering

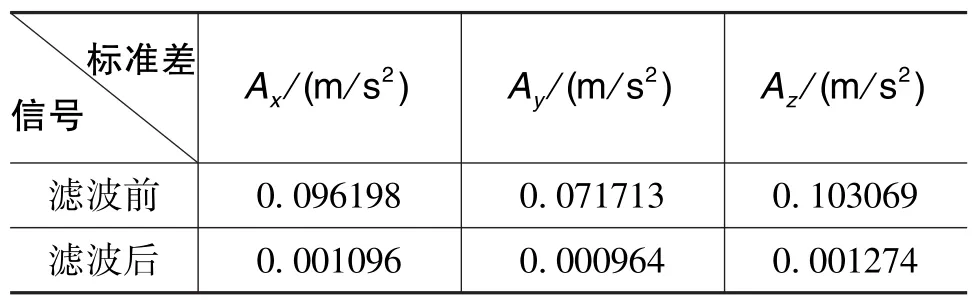
表4 小波預濾波前后加速度計標準差Table 4 Standard deviation of Accelerometer before and after wavelet pre?filtering

4.2 對準結果

傳統初始對準算法和基于小波預濾波的初始對準算法，Kalman濾波的初始值P、Q、R取值不變，小波預濾波前后對準姿態角隨時間的變化曲線如圖7所示，表5為預濾波前后6次對準結果和標準差。

從圖7可以看出，經過小波預濾波處理后，姿態角的收斂速度明顯加快。濾波前精對準時間在100s以上，濾波后航向角在精對準50s即可達到較高精度，且收斂過程平穩性更高。表5給出了預濾波前后6次對準的結果，預濾波前，僅基于慣性系粗對準和Kalman濾波時，航向角的均方差為6.08′；預濾波后，航向角的均方差為2.77′。

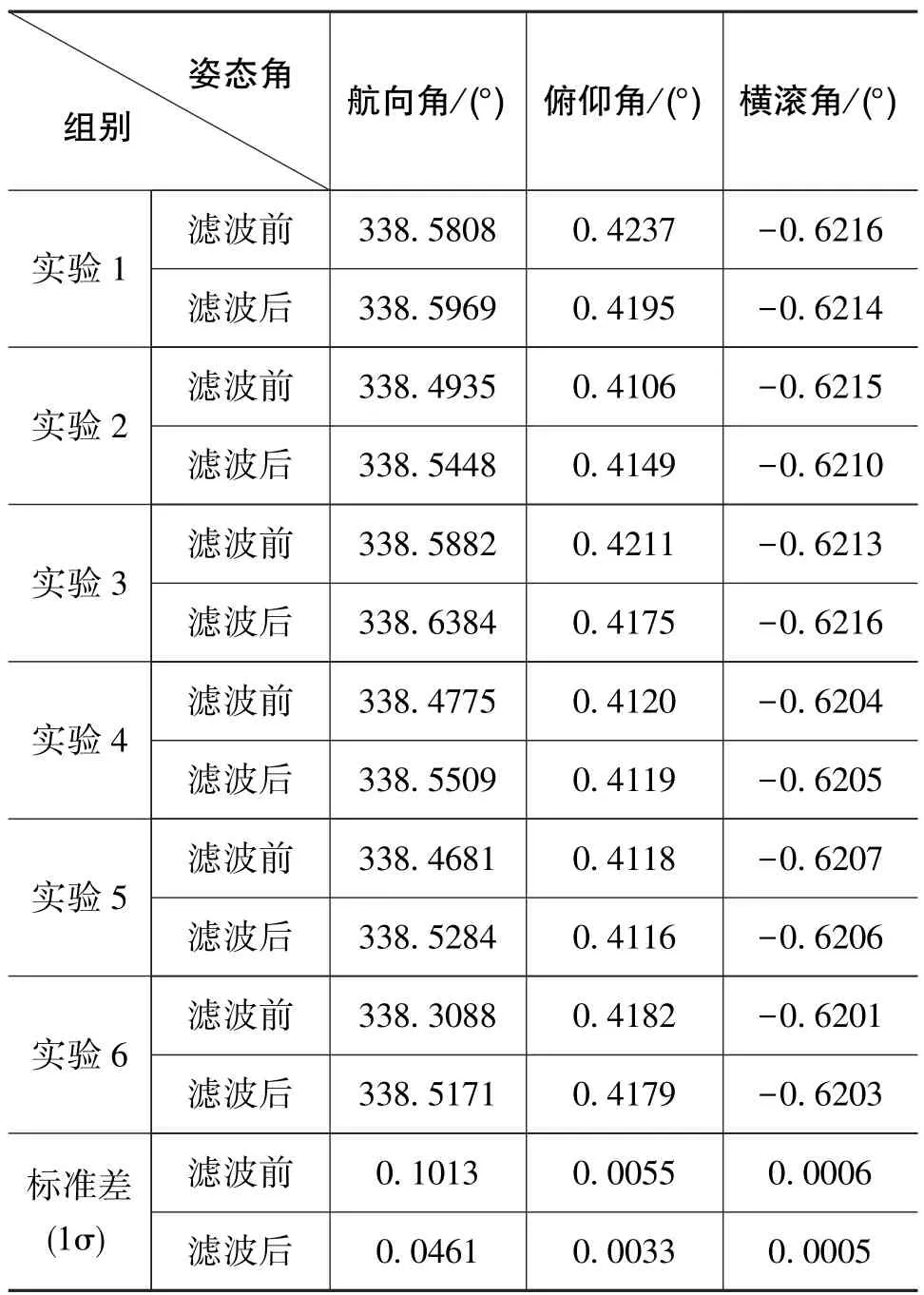
表5 預濾波前后6次對準結果和標準差Table 5 Six alignment results and standard deviation before and after pre?filtering

5 結論

晃動基座帶來的角運動和線運動的干擾是影響慣導系統初始對準的重要誤差源，本文綜合考慮對光纖陀螺儀和加速度計的濾波效果和濾波的實時性，針對實測光纖捷聯慣導系統的輸出信號，設計出一種小波實時預濾波算法，并進行了基于慣性系的粗對準和Kalman濾波精對準的半實物仿真實驗。實驗結果表明，該方法既能滿足實時性的要求，又能有效抑制光纖陀螺和加速度計的高頻噪聲。濾波前后，陀螺儀和加速度計的均值幾乎不變，而陀螺儀的輸出噪聲降到了濾波前的10%以下，加速度計的輸出噪聲降到了濾波前的5%以下，能夠實現晃動基座下的快速、精確自對準，具有一定的工程應用價值。