基于PSD的并聯微定位平臺位姿檢測方法

荊龍賓，梁 康，黃山云，閆軍偉，夏 剛

（1.北京航天控制儀器研究所，北京100039；2.中國人民解放軍國防大學聯合勤務學院，北京100039；3.中國航天電子技術研究院，北京100094）

0 引言

并聯機構是國際上機械裝備研究領域的熱點課題，它是知識密集型和技術密集型高度結合的機電一體化高科技產品，是并聯運動機構學、計算機學、控制理論、精密測量、多體系統等多學科理論研究的交叉領域。并聯機構除了具有承載能力強、剛度高、動態響應特性好的優點外，還有一個突出的特點就是具有很高的機械綜合精度和控制精度，其在并聯運動機床、并聯機器人、定位裝置、測量裝置、飛行模擬器、醫療、娛樂等諸多領域得到了廣泛的應用。

研究表明制造和裝配引起的幾何誤差是造成并聯機構末端位姿誤差的重要原因［1］，如何對平臺進行位姿檢測以進行精度標定是研究并聯平臺的一項重要內容。Chiu等［2］利用安裝在靜平臺和動平臺之間的可伸縮桿，實現了對Hexapod并聯機床的精度檢測。邵珠峰等［3］借助靜平臺上的標準定位圓孔，通過儀器對拉線式編碼器進行標定，進而利用線尺在線測量、記錄機構中的實際位姿，結合數控系統中的理論軌跡，實現了3?RRR并聯機構的參數辨識。上述方法均為自標定的檢測方法，自檢測方法的不足在于有些機構的被動鉸鏈安裝傳感器時較為困難甚至是不可能的［4］。外部檢測法利用外部傳感器檢測末端位姿信息，并構造它們與模型計算值之間的殘差，進而通過相應的逆解或者正解辨識模型來識別幾何參數。Rauf等［5］通過使用一套包括雙軸傾角傳感器、線性可變差動變壓換能器以及旋轉傳感器的設備為測量手段對六自由度的HexaSlide機構進行了精度檢測研究，使其精度得到了大幅度提高，但魯棒性相對較差。Traslosheros等［6］以計算機視覺為測量手段對并聯機構的精度檢測進行了研究，經濟性更強，但這類方法受視覺系統測量精度的限制，對最終的精度檢測結果有較大的影響。羅繼曼等［7］提出了一種利用激光檢測儀和最小二乘算法對并聯機器人進行精度標定的研究方法，精度較高，但結構復雜，經濟性較差。

本文以六自由度并聯微定位平臺為研究對象，基于二維PSD位置傳感器提出一種非接觸式光學檢測方法，建立了位姿檢測的理論模型，在此基礎上設計了一套位姿檢測系統。仿真分析驗證了理論模型的正確性，同時用該方法進行了誤差分析。結果表明，本文設計的這套檢測系統能實時在線測量平臺位姿，并且集成在定位平臺里，具有體積小、結構簡單可靠、可操作性強等優點。

1 二維PSD光電位置傳感器

PSD（Position Sensitive Detector）位置探測器是利用半導體橫向光電效應實現對入射光點位置進行檢測的一種光電器件，與傳統的象限電池、CCD相比，PSD具有位置分辨率高、響應速度快、不需要掃描、處理電路簡單等優點。此外，還由于PSD是非分割型元件，可連續輸出模擬信號，無死區，位置輸出信號只與入射光的中心位置有關，對光斑形狀無嚴格要求，因而光學系統比較簡單。二維PSD工作原理如圖1所示。

從圖1可知，通過表面的p型電阻層檢測X方向的位置，通過里面的n型電阻層檢測Y方向的位置。這時，由于n＋層內的電荷分布不勻形成電流，用此電流進行檢測，這時電流方向是流向PSD內［8］，光點的入射位置與電流之間有如下關系：

式中，I0為總電流，I0＝Ix1＋Ix2＝Iy1＋Iy2；Ix1為X方向電極1的電流；Ix2為X方向電極2的電流；Iy1為Y方向電極1的電流；Iy2為Y方向電極2的電流；Lx為X方向電極間（受光面）長度；Ly為Y方向電極間（受光面）長度；x是坐標軸以受光面為中心時光入射位置的X坐標；y是坐標軸以受光面為中心時光入射位置的Y坐標。

可求出光入射位置坐標：

2 位姿檢測系統理論模型的建立

圖2所示為六自由度微定位平臺模型，平臺結構由上下平臺及6根電動缸支桿組成。其中，下平臺為定平臺，上平臺為動平臺，電動缸與上下平臺之間分別由6個球鉸連接。伺服電機驅動6根電動缸的伸縮達到精確控制上平臺位姿，實現上平臺的定位目的。

六自由度微定位平臺的結構參數如圖3所示。圖3中，ra為上絞圓半徑，rb為下絞圓半徑，α為上絞點與中心連線與坐標軸夾角，β為上絞點與中心連線與坐標軸夾角，H為平臺高度，h為質心高度。

在此平臺基礎上建立位姿檢測系統，系統理論模型如圖4所示，為便于觀察和計算，將其放入立體三維坐標系里。在圖4中，A點為激光原點，與上平臺固連，①②③分別為3個二維PSD探測器，放置于與下平臺固連在一起并平行于下平臺的工裝板上，3個探測器組成邊長為t的正三角形，激光原點到探測器平面的距離為l，A在探測器平面上的初始零位投影點為坐標系原點O。當動平臺沿X軸、Y軸、Z軸平移及繞X軸、Y軸、Z軸轉動時，激光點在3個PSD探測器上有相應的位移量，建立6個位移量與6個自由度的變化量之間的關系式，反解出動平臺的位移及轉動量，現分別求動平臺沿X軸、Y軸、Z軸平移及繞X軸、Y軸、Z軸轉動時PSD探測器上相對應的位移量。設3個PSD探測器上X、Y方向上的位移量分別為ΔX1、 ΔY1、 ΔX2、 ΔY2、 ΔX3、 ΔY3。

（1）動平臺沿X軸平移a個位移

（2）動平臺沿Y軸平移b個位移

（3）動平臺沿Z軸平移c個位移

（4）動平臺繞X軸轉動α個單位（方向遵循右手法則）

動平臺繞X軸轉動1周，與②號PSD相對應的激光線形成的錐面方程為：

與平面z＝0聯立解為：

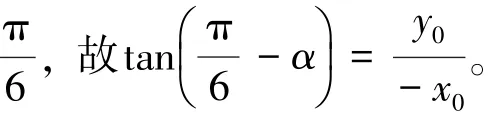
可得：

將式（14）代入（13）得：

（5）動平臺繞Y軸轉動β個單位

同理，可得如下公式：

（6）動平臺繞Z軸轉動γ個單位

將上述六組（ΔX1， ΔY1， ΔX2， ΔY2， ΔX3，ΔY3）分別相加，即為動平臺沿X軸、Y軸、Z軸平移及繞X軸、Y軸、Z軸轉動時PSD探測器上相對應的位移量，得到未知數為a、b、c、α、β、γ的一組非線性方程組。

3 理論模型驗證

此處運用擬牛頓法（Broyden 方法）［9］求解非線性方程組。牛頓法每迭代一次，就要計算當前一步的Jacobi矩陣的逆矩陣，計算量比較大。為了解決逆矩陣問題，設法構造一個矩陣，逼近逆矩陣，即為擬牛頓法。Broyden方法基本迭代格式為：

其中， Δxk＝xk＋1－xk，yk＝f（xk＋1）－f（xk）。

在Matlab中，運用Broyden方法求解上節的非線性方程組。設定迭代次數為2000次，有針對性地選取幾個有代表性的位姿坐標，并求解計算值與理論值之差，結果如表1所示。

由表1結果可知，在有限次的迭代計算中，選取的位置姿態坐標計算值與理論值之差小于10－5mm，驗證了理論模型的解算是正確和可行的，且具備較高的迭代精度。

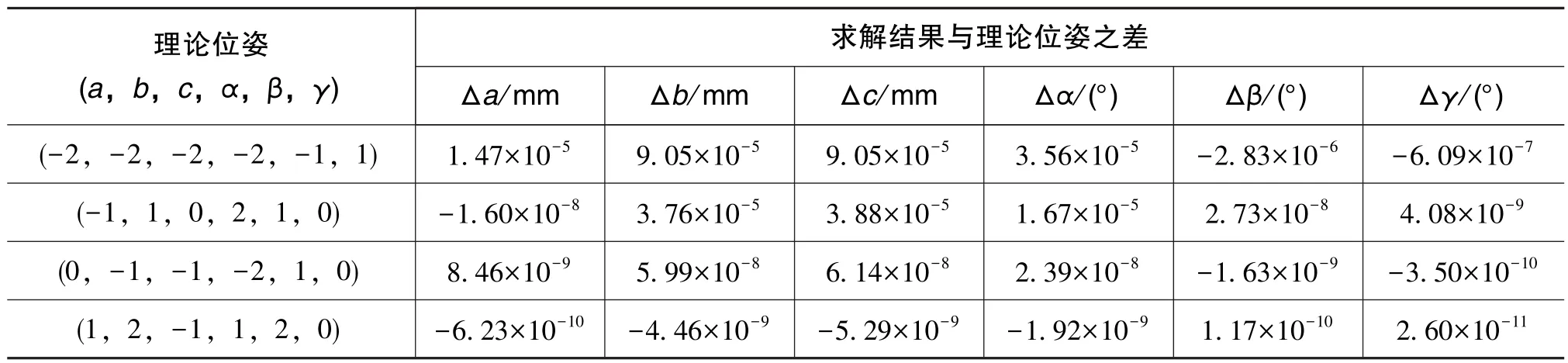
表1 計算結果Table 1 Results of calculation

4 誤差分析

4.1 誤差源

本文研究的六自由度微定位平臺的位姿測量誤差的來源主要有3個方面：1）位姿檢測系統加工裝配誤差（含工裝加工尺寸誤差、安裝調試空間位置誤差）；2）激光源照射誤差（含光斑形狀、光斑抖動誤差）；3）PSD位置傳感器位置測量誤差（含PSD測量精度、電噪聲誤差）。其中，加工裝配誤差在對PSD做初始化的時候進行補償，故影響測量精度的誤差主要是激光源照射和PSD位置傳感器測量誤差。

4.2 誤差仿真分析

在Matlab軟件內，PSD測量值疊加一幅值為0.01mm的隨機噪聲，計算此時二維PSD存在測量噪聲時解算的實時位姿，并與理論位姿進行比較。選取4個典型位姿進行分析，結果如圖6所示。

進一步對100次誤差迭代結果取均方根值，結果如表2所示。

表2 6個自由度誤差均方根值Table 2 Root mean square value of six degrees

從圖6及表2可以看出，PSD位置傳感器測量誤差導致的平移誤差在0.01mm之內，轉動誤差在0.002°之內。結果表明，該系統能夠快速準確解算六自由度定位平臺位姿，同時具備較高的測量精度。

5 結論

本文基于PSD位置傳感器設計了六自由度光學位姿檢測系統，在理論分析的基礎上建立了姿態解算的數學模型，并做了仿真分析，分析結果驗證了姿態解算模型的正確性。針對姿態解算模型，進一步進行了誤差分析。分析結果表明，本文設計的光學檢測系統能同時解算并聯平臺的6個位姿，同時具備較高的測量精度，平移誤差在0.01mm之內，轉動誤差在0.002°之內。