慣導平臺長時間通電有限元熱分析

關永祥，汪立新，王 琪，劉德俊

（火箭軍工程大學，西安710025）

0 引言

為應對新形勢下的工作任務，要求延長慣導平臺的一次連續通電時間。研究表明，平臺系統的溫度變化是限制長時間通電的主要因素。慣性儀表具有苛刻的使用條件，溫度梯度不平衡會造成陀螺馬達質心位移，溫度上升的高低會影響陀螺馬達的壽命［1］。平臺臺體軸受熱會發生變形，導致金屬六面體的安裝精度發生變化，從而使以金屬六面體為安裝基準的其他慣性儀表的安裝精度跟著發生變化。軸系間的配合間隙也會發生變化，使得軸承的摩擦力矩增大或者減小，使得平臺的漂移誤差加大［2］。因此，有必要對長時間通電的慣導平臺進行熱分析，設計溫度控制方法。

以往常采用試驗及模擬計算的方法來進行平臺的熱分析。鄧益元［3］在靜壓液浮陀螺平臺恒溫控制系統的熱分析中，利用Fourier、Newton、Boltz?mann等經典傳熱公式，從網絡熱阻入手，對平臺的傳熱途徑及方式進行了初步分析。但由于平臺結構復雜，很難保證計算的準確性，使得平臺熱分析符合實際。吳亞明等［2］利用有限元就溫度變化對平臺裝配精度、軸承預緊等方面所產生的影響進行了分析，并從平臺裝配工藝角度提出了減小熱變形影響的具體措施。楊盛林等［4］利用有限元法和傳熱學理論，確定了平臺的環境溫度適應能力，著眼于結構設計，對平臺中的強化換熱提出了改進方案。劉昱等［5］利用有限元進行了熱流場仿真分析，設計了半導體制冷技術，有效地控制了某型光纖陀螺慣導平臺的溫度場。黃小凱等［6］利用有限元進行了慣性平臺熱?結構耦合分析，得到了平臺殘余應力隨溫度循環應力的釋放規律。馬一通等［7］利用阻值比較法，為平臺設計了一種高精度多路溫度采集方法，實現對64路溫度的采集，測溫精度達±0.02℃。徐峰濤等［8］采用流固耦合傳熱的方法，利用Fluent軟件得到了某小型化平臺臺體溫度場平衡點及系統的溫度場分布規律。

本文將采用ANSYS三維瞬態熱分析方法模擬平臺內部熱傳導以及對流換熱的傳熱過程，對氣浮陀螺慣導平臺的溫度場開展研究，以尋求長時間通電平臺溫度變化規律。

1 有限元物理模型

氣浮陀螺慣導平臺系統復雜的結構組成導致分析熱物理問題時，很難把所有影響換熱的因素都考慮進去，有必要對平臺的物理模型結構和材料組成進行簡化處理。

在嚴格控制模型簡化帶來的溫度和熱流誤差的基礎上，根據功耗估算和實際傳熱情況，忽略傳感器、變換器、電子線路及氣路等對傳熱和換熱影響較小的部件，對陀螺、加速度計、電機、框架等結構復雜的部件做一體化處理。應用Solid?works軟件繪制平臺實體，簡化后的三維模型及其爆炸視圖如圖1所示。

平臺系統各器件的材料組成較為復雜，準確計算熱容量很困難，同樣也需要采用合適的簡化處理。上下帽蓋、平臺臺體和內外框架、基座均為鋁合金，其密度、比熱容、熱導率等熱物性參數相近；陀螺儀材料為鈹，加速度計、氣浮擺、電機材料大體為不銹鋼［1］。 材料熱物性參數如表 1 所示［9］。

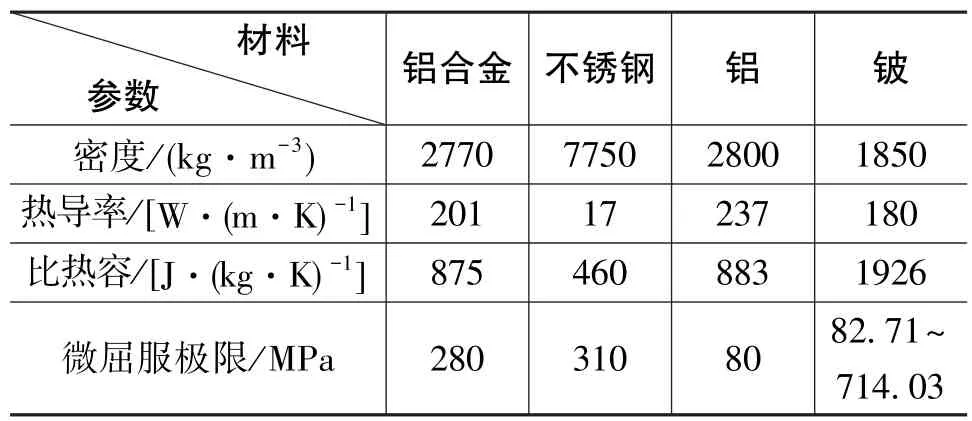
表1 材料性能參數表Table 1 Parameters of material performance

實體建模完成后，對其進行網格劃分。為了保證計算結果的精確性，采用了三維二十節點六面體熱分析單元Solid90和三維十節點四面體熱分析單元Solid87，最后得到節點和單元數目分別為692855個和390899個。有限元網格模型如圖2所示。

2 數學模型及邊界條件

有限元熱分析計算需要的條件包括：慣導平臺的構形、內部儀器設備的布置、幾何尺寸、材料熱物理性質、儀器設備的發熱量、熱控制狀態等。構造了平臺有限元模型后，利用ANSYS軟件，在初始條件T＝T（x，y，z，t0）下，根據導熱微分方程和溫度邊界條件即可以求解其瞬態溫度場。

導熱微分方程是根據熱力學第一定律和Fourier定律所建立起來的描述物體溫度隨空間和時間變化的關系式，是導熱過程的能量方程：

式中，ρ為密度，c為比熱容，λ為導熱系數，qv為單位體積單位時間內所發出的熱量。

慣導平臺中存在3種傳熱途徑：傳導、對流和輻射。由于平臺總體熱源溫度不高，平臺的輻射換熱作用不強，在此不予考慮［3］。傳導和對流的溫度邊界條件通常有3類：

1）已知任何時刻物體邊界面上的溫度值（第1類），即：

式中，tw是溫度在邊界面s的給定值。

2）已知任何時刻物體邊界面上的熱流密度值（第2類）， 即：

式中，qw是給定的通過邊界面s的熱流密度，n為換熱表面外法線方向。

3）已知邊界面周圍流體溫度和邊界面與流體之間的表面傳熱系數h（第3類），根據Newton冷卻定律，該邊界條件可以表示為：

式中，ts為表面溫度，tf為流體溫度。

在變溫條件下，平臺熱應力滿足廣義Hooke定律，也就是熱應力彈性本構方程［10］：

平臺瞬態分析的邊界條件取決于其工作時的實際情況。結合試驗數據計算結果，采用第1類和第3類邊界條件，設定了通電27000s內的溫度載荷。臺體、內框架、外框架與空氣對流換熱系數為10W/（m2·K），陀螺、加速度計與空氣對流換熱系數為 80W/（m2·K）。

3 有限元計算結果及分析

3.1 溫度場計算結果與分析

平臺的初始溫度為19.5℃，由設定的求解條件可以得到平臺通電27000s內各部件的溫度分布，并可以模擬溫度場隨時間的動態變化過程。由計算結果可得平臺總熱通量分布圖、通電40s溫度場分布圖和通電27000s溫度場分布圖，如圖3～圖5所示。

從圖3可以看出，平臺主要以熱傳導方式進行傳熱。主要熱源 （3個陀螺儀和2個陀螺加速度計）產生的熱量傳導至臺體上，臺體上的熱通過臺體軸兩個軸端傳到平臺內框架，再通過內框架軸端傳到外框架上，接著由外框架軸端傳到平臺基座及上下帽蓋，最后傳到環境中，腔內通過對流換熱作用使內部空氣溫度升高。熱通量最大值為80300W/m2，位于X陀螺加速度計。總體看來，平臺熱流量密度較大，在通電過程中造成的熱能傳遞效應明顯。

在瞬態分析中，設置時間的最小步長為40s，所以在第40s時的模擬結果最為接近初始溫度場。由圖4可知，在平臺腔外只有基座兩邊的力矩電機作為熱源，且發熱量較小，熱交換作用不明顯；腔內的熱源有臺體上的陀螺儀和加速度計以及框架軸端的力矩電機，陀螺儀與加速度計和平臺臺體接觸產生明顯的熱交換作用，且加速度升溫較陀螺儀快，力矩電機發熱量較小，各部件仍為初始溫度19.5℃。

通電27000s時，基座溫度場分布云圖中，由于電機發熱作用以及內部的傳導作用，電機兩側溫度較高，且呈現對稱變化，由外框架中心對稱兩側也可大致看出溫度變化的對稱形式。平臺內部整個熱交換過程仍在進行，各部件溫度顯著升高，溫度場分布不均勻。最高溫度為X陀螺加速度計的53℃，最低溫度為平臺帽蓋的27℃，二者溫差約26℃。此時，高溫區域主要位于平臺臺體，隨著通電時間的延長，在達到熱平衡狀態之前，各部件溫度將繼續升高。

3.2 臺體熱應力場分析

通過對平臺的溫度場分析，可以得到各部件工作時的溫度值。鑒于溫度場對臺體的影響可直接導致系統精度的降低，下面對臺體的熱應力場進行分析。將所得溫度結果讀入結構分析模塊，作為溫度載荷，在結構分析中設定臺體位移值為0，將其作為位置約束條件，即可求得熱應力值。經過計算，得到的應力和熱變形分布如圖6所示。

由計算結果，得到應力的最大值為374.72MPa，應力的最大值出現在陀螺儀表安裝面上。根據表1所提供的數據，鋁合金的微屈服極限為280MPa。計算所得熱應力值遠超過許可值，臺體結構尺寸的穩定性將不再得到保證。另外，由圖6（b）可知，臺體最大變形位移約0.17mm，位于臺體X向邊角處，兩軸端附近變形大約為0.037mm。臺體各安裝面都產生了較大的熱應力，熱應力的存在直接影響陀螺儀表位置的微變形。另一方面，引起軸承裝配尺寸的變化，進而影響軸承的預緊力和摩擦力矩，降低了系統工作精度。

3.3 溫度變化曲線與分析

計算可得陀螺、加速度計、腔內與臺體的溫度變化曲線，如圖7所示。由圖7可知，陀螺和加速度計作為平臺的主要熱源，它們的溫度變化引發了其他部件的溫度變化，腔內與臺體的溫度變化趨勢大致與之相同。起初，隨著通電時間的增加，溫度上升都比較快。當通電7200s后，溫度上升速度有所減緩。

通電27000s時，3個陀螺的溫度變化約23℃，最高溫度不超過45℃。Z加速度計溫度上升變化與X加速度計和Y加速度計相差較大，Z加速度計最高溫度約45℃，X加速度計、Y加速度計最高溫度近55℃，溫度變化約35℃。這是由于其各自發熱量不同，Z加速度計為線性加速度計，X加速度計、Y加速度計為陀螺加速度計，陀螺馬達的運轉所產生的熱量較多。臺體溫度介于陀螺和加速度計之間，上升至47℃，符合傳熱的實際情況。加速度計和陀螺均安裝在臺體表面，熱傳導作用使得臺體的溫度介于高溫與低溫之間。腔內氣體溫度上升至約40℃，并可看出曲線漸趨平緩，表明腔內溫度將達到熱平衡狀態。

為進一步分析平臺各部件溫度趨勢，通過運用Matlab仿真軟件對各曲線進行擬合。經計算得到溫度擬合曲線，如圖8所示。

由圖8（g）可以看出，平臺最終能達到熱平衡狀態。熱平衡狀態下，各部件溫度將穩定于一數值。陀螺溫度約43℃，X加速度計、Y加速度計溫度約55℃，Z加速度計溫度約47℃，臺體溫度約49℃，腔內溫度約42℃。

熱平衡試驗溫度穩定判據GJB 1033A?2005規定，在連續4h內測點溫度波動值不超過±0.5℃或者連續4h內溫度單調變化小于0.1℃就達到穩定。由仿真結果可得每4h腔內溫度變化，如表2所示。由表 2可以看出，通電 12h～16h溫度升高0.26167℃，由此可判定，平臺通電12h達熱平衡狀態。

表2 腔內溫度變化Table 2 Temperature variations in intracavity

3.4 試驗數據對比

將腔內溫度仿真結果與試驗數據對比，仿真試驗對比如表3和圖9（a）所示。 圖9（b）為實測值擬合結果圖，其每4h腔內溫度變化如表4所示，經計算一樣能夠判定通電12h平臺達到熱平衡狀態。

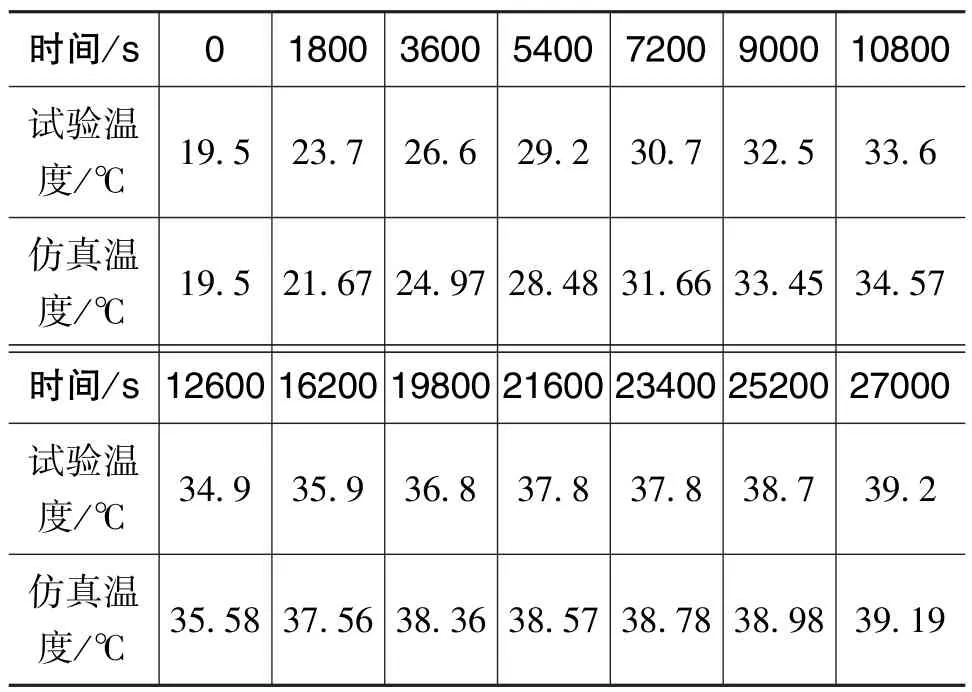
表3 仿真試驗數據對比表Table 3 Comparison of simulation test data

表4 腔內實測溫度變化Table 4 Measured temperature variations in intracavity

對比仿真結果和試驗結果可知，仿真結果與試驗結果趨勢基本吻合，證明了仿真結果的正確性；仿真數值與試驗數值存在誤差，且誤差波動不穩定，還需要進一步修正仿真的參數。

4 結論

利用有限元軟件ANSYS，對慣導平臺長時間通電溫度場分布進行了仿真研究，得到了平臺在連續通電過程中的溫度場分布圖及溫度隨時間的變化規律，并通過試驗數據對比驗證了仿真結果的正確性。具體總結如下：

1）平臺通電過程中的溫度場變化以熱傳導方式為主，主要熱源是陀螺加速度計和陀螺儀，臺體在傳熱過程中起中樞作用，將熱源熱量不斷向四周擴散，平臺溫度場分布極不均勻。

2）初始溫度19.5℃，當通電27000s時，陀螺和加速度計溫度上升明顯，陀螺溫度升高至40℃，X加速度計、Y加速度計升至55℃，Z加速度計升至45℃；熱傳導作用使臺體溫度升至47℃；由于對流傳熱造成平臺腔內溫度升高約20℃，隨著通電時間的延長，各部件和腔內都將達熱平衡狀態。

3）受熱應力作用，臺體產生微變形，最大變形位移約0.17mm。

4）平臺各部件和腔內達熱平衡狀態的時間大致相當，約需通電30000s。