屬性排序的粗糙集和統計方法研究

張先韜

(1.中煤科工集團重慶研究院有限公司， 重慶 400039；2.瓦斯災害監控與應急技術國家重點實驗室， 重慶 400039)

粗糙集是數據處理方法中的一種有效的軟計算工具，由波蘭數學家Pawlak于1982年提出[1]。它是一種刻畫不完整性和不確定性問題的新型數學工具[1]，能有效分析和處理不精確、不一致、不完整等各種不完備的信息，并從中發現隱含的知識，揭示潛在的規律[1]。 經過多年發展，隨著大數據、互聯網、移動應用、智能算法等的不斷發展和現實應用需求的不斷提出，粗糙集理論和方法被越來越多的行業領域和專家學者所使用[2-11]。在醫療、機器學習、模式識別、數據處理、互聯網等多個行業和領域均發揮著其作用，而且越來越多的地方正在探索和嘗試使用粗糙集方法與其他方法交叉結合以期對所研究問題獲取更好的解決方案[2-11]。

在粗糙集理論中，屬性約簡是將數據庫或數據系統中的信息進行合理的篩選，將冗余信息屏蔽或刪除，大大簡化數據信息表達而不影響研究需求或簡化信息至可控范圍[8]。在經典粗糙集理論中，計算信息表中各屬性的重要度，可以計算出各個屬性的重要性數值度量，直接進行屬性重要性量化比較并進行排序。在多學科交叉研究中很多學者采用粗糙集方法進行排序、評價、預測研究[9-11]，對部分數據表的信息研究是一個很好的方法，但是這種計算方法也有缺陷。在信息系統中計算屬性重要度可能存在數值相同的情形，這種情形很普遍[12]，對于很多研究產生了局限性，單純使用粗糙集方法不能滿足屬性重要性唯一鏈式排序的研究需求。本文在研究中將粗糙集方法和統計學方法相結合，使用層級計算的方式，在同一標準下解決小規模數據系統中屬性重要度相同無法進行屬性重要性唯一鏈式排序的實際需求。

1 粗糙集基礎知識

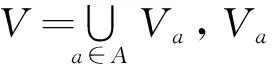
在決策中，對于每個子集B?C，定義[12-13]IND(B)={(x,y)∈U2|f(x,b)=f(y,b), ?b∈B}[12-13]。IND(B)是等價關系，可以不加區分地用B表示。對任意的B?C和x∈U，記[x]B={y∈U|f(x,a)=f(y,a), ?a∈B}，稱[x]B是對象x在屬性集B下的等價類。記U/B={[x1]B, [x2]B,…,[xn]B}，稱U/B是屬性集B對論域構成的劃分[12-13]。

在信息系統I=(U,A,V,f)中，對子集X?U和屬性集B?A，定義[12-13]：

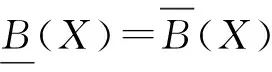
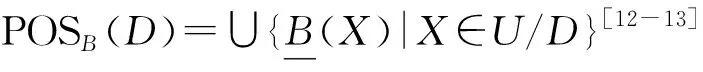
建立數據表并使用粗糙集方法進行研究，目的就是從數據表中去掉對于分類沒有影響的條件屬性或子集，去掉后不影響系統的分類能力，即保持其知識表達能力不變，這個過程就是屬性約簡。在粗糙集理論中，通過計算屬性重要度或其他方法可以獲取信息系統的約簡，在小規模信息系統中，約簡可以窮舉。在某些實際問題研究中可以通過計算屬性重要度對屬性重要性程度進行排序，重要度為0的屬性去掉以后不影響信息系統的知識表達。該方法計算的屬性重要度可能存在數值相同的情形，在不允許出現并列的排序問題中，需要進一步處理區分數值相等的屬性的重要程度以期獲得唯一性排序。下面介紹研究中使用粗糙集屬性重要度、約簡結合統計學方法進行屬性排序的處理方法。

2 基于粗糙集屬性重要度的一級排序

以研究中使用的決策表為例[13-16]，數據表為重慶市冬夏季節碳排放影響因素研究數據采樣統計結果，數據表有136個不重復對象，決策屬性D1、D2分別為冬季、夏季碳排放量，條件屬性a1～a11為影響住宅建筑碳排放的11個影響因素，分別為住房歸屬、建筑使用時間、建筑層數、所住樓層、住房面積、家庭平均年齡、家庭常住人口數、最高文化水平、家庭人均年收入、節能意識、能耗設備平均使用年限，各屬性值的意義不影響本文所述研究方法的使用，故不再給出。因篇幅原因，決策表數據不宜在本文中全部給出，表1給出簡表。

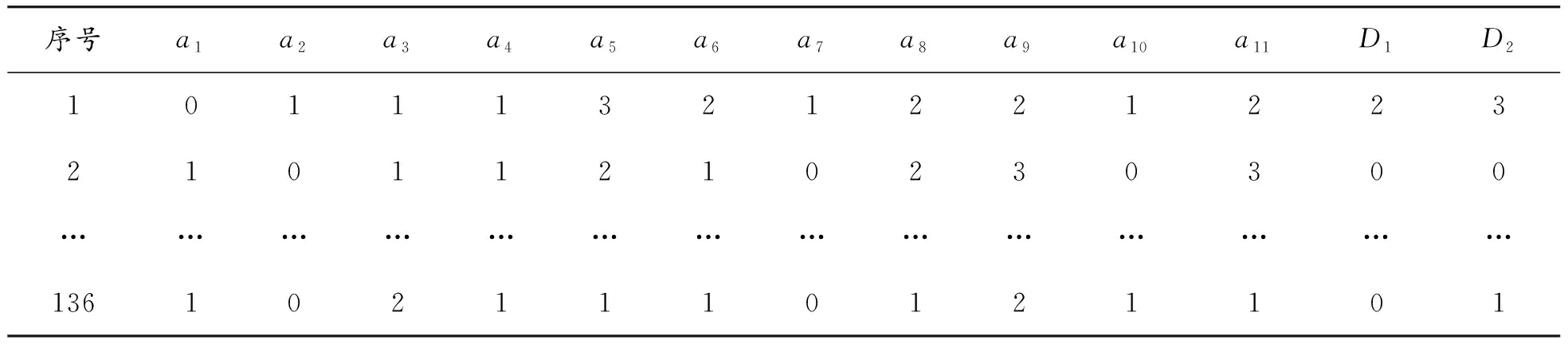
表1 決策數據表(簡表)

首先使用本文提到的粗糙集屬性重要度的計算方法計算各個屬性的重要性度量，這種計算方法科學合理，使用粗糙集方法進行不確定信息處理和數據挖掘過程中已經被廣泛使用，通過這種方法進行量化計算和排序準確可靠，計算得到在不同決策下各個屬性的重要度如表2所示。

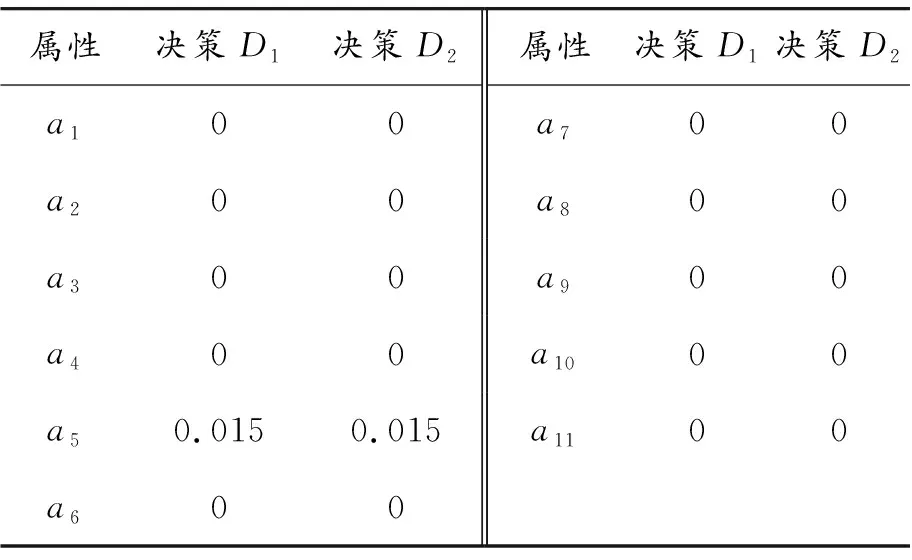
表2 屬性重要性的數值度量

據表2可知：決策D1數據表中屬性a5的重要度為0.015，a5比其他單個屬性重要。決策D2數據表中屬性a5的重要度為0.015，a5同樣比其他單個屬性重要。計算屬性重要度進行重要性排序是綜合數據表信息的全局宏觀信息排序，屬性重要度大的在重要性排序中占全局靠前，但是對于其他屬性而言，單個屬性的屬性重要度均為0，無法通過計算屬性重要度的方法決定這些相對重要屬性重要程度的全局排序，無法對屬性進行唯一鏈式排序，結果不能直接適用于所研究問題。為了通過數值度量計算和區分各屬性的重要性，體現出各個屬性的不同影響程度并實現排序，下面給出結合粗糙集約簡理論和統計方法的屬性排序方法。

3 基于約簡的屬性頻次統計二級排序

本文第2節使用粗糙集屬性重要性度量計算了各屬性的重要度數值，但不能滿足所研究問題的需求，本節介紹使用粗糙集約簡理論和統計方法的二級排序方法。為了實施本節處理方法，需要使用粗糙集約簡理論計算該決策表在決策D1和D2下各自的全部約簡。由于所研究問題獲取到的決策表數據規模較小，可以對該決策表約簡窮舉。

根據統計學理論和約簡的意義，在窮舉得到的所有約簡中，單個屬性出現的頻數差別可以體現屬性的重要程度，出現次數越多屬性越重要。頻數又可以除以所有約簡的數量轉換為比例數值，通過數值化的統計結果可以對屬性的重要程度進行排序。這是一種按照等級的排序，頻數(比例)越大重要等級越高，頻數(比例)越小重要等級越低，頻數(比例)相同重要等級相同。此方法使用統計學原理，可以保證數據表信息的客觀性和正確性，從全局信息出發保持數據表信息不變的情況下得到統計數據結果，方法有理論依據支持，計算得到的數值度量結果科學可靠。由此，將得到的約簡進行轉換，使用數據表表示，用表格的形式表示對象的有無(0表示約簡中無該屬性，1表示約簡中有該屬性)，簡表見表3。

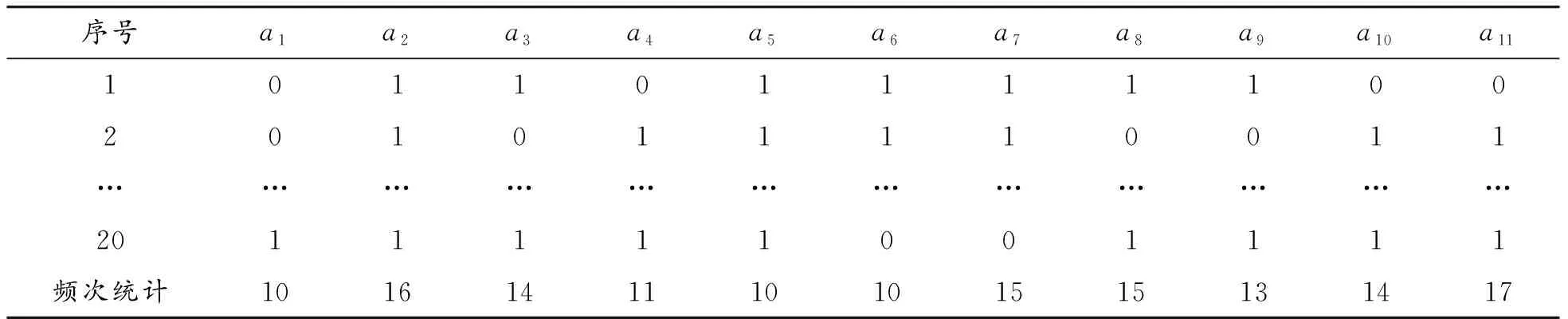
表3 決策D1數據表約簡的數據表(簡表)

根據表1、3可以按照本節所述頻次統計法計算得到不同決策下屬性重要性的有效數值度量，見表4。

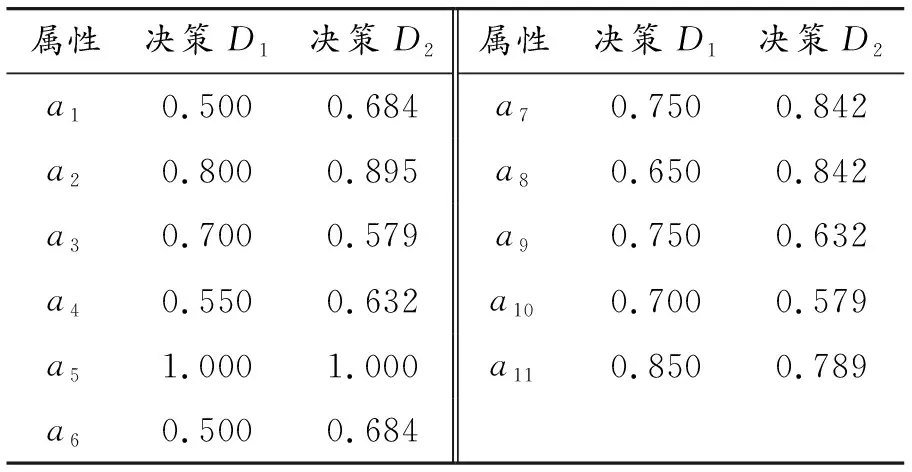
表4 屬性重要性的數值度量

由此可以在不同決策下進行屬性重要性由高到低的初次排序，結果見表5。

從表5可知：使用粗糙集屬性重要度的計算方法得到的屬性排序中，對冬季決策而言屬性a9和a7重要性相當、a10和a3重要性相當、a6和a1重要性相當，對夏季決策而言屬性a7和a8重要性相當、a6和a1重要性相當、a9和a4重要性相當、a10和a3重要性相當。在排序過程中使用粗糙集的屬性重要度無法區分這些數值量相同的屬性的重要性程度，在所研究的問題中無法完成排序問題的最終結果。為了區分這些屬性以實現研究問題所需的屬性排序，下節介紹一種基于約簡的屬性影響程度均值三級排序方法。

4 基于約簡的屬性影響程度均值三級排序

在獲取全部約簡后，在約簡中去掉某屬性后屬性子集的重要度會減小，可以使用這一點量化計算重要度變化值的平均值(稱為平均影響程度)，以實現屬性的重要性(影響)區分。某屬性的重要度變化越大則其在約簡中的影響/作用就越大，這符合客觀規律和理論實踐，根據平均值理論全部約簡中這種影響的平均值越大則該屬性的影響越大，可以視為該屬性越重要，由此可以由定量計算轉換成定性排序。

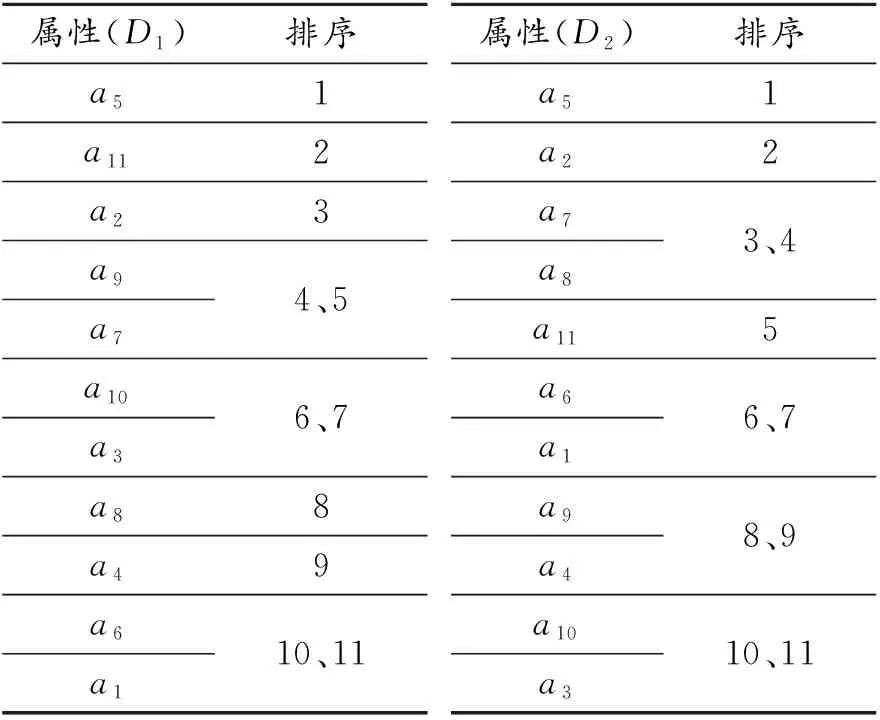
表5 決策表重要性由高到低二級排序

粗糙集屬性重要度數值計算是基于數據表全局信息的量化計算方法，本節是基于數據表局部細化信息的量化計算方法。這種考量方法執行細節計算，實現從定量到定性的局部轉換，比粗糙集屬性重要度計算的方法等級或層次、級別低，可作為輔助計算方式，但是這種考量方法仍保持在同一標準下執行數值計算比較，任何一個約簡均包含不影響系統研究的全部信息(不改變系統分類能力)，執行數值差計算時考量的是全局約簡和同一屬性，計算結果使用平均值度量，這樣計算未改變度量標準和全局信息，具有可行性和說服力，可以獲得理論和實踐上的有效支撐，在本文所引用的實際問題中可以發揮作用，用來區別兩個屬性的重要程度。稱這種方法為基于約簡的影響程度均值三級排序方法，下面介紹該方法的具體實施過程。

在決策D1數據表中為了區分a7、a9，分別計算其所在約簡的重要度和去掉這個屬性后的屬性子集的重要度，對這兩個數值作差，然后對得到的這些數值求平均，平均值越大屬性重要性越大，由此實現這兩個同等級屬性的重要性排序，對于冬季碳排放決策表中的a3、a10和a1、a6和夏季碳排放決策表中的同等級屬性均采用此方法進行重要性區分排序。對冬季碳排放影響因素中重要程度概率結果相同的屬性進行區分計算，計算結果如表6、7所示。

表6 決策D1數據表中屬性a7的平均影響程度計算

表7 決策D1數據表中屬性a9的平均影響程度計算

由表6、7可知：在決策D1數據表中屬性a9的平均影響程度比屬性a7大，在重要性排序中a9比a7重要。對決策D1數據表中的屬性a3、a10和a1、a6，可以使用相同方法進行計算。a3的平均影響程度為0.202，a10的平均影響程度為0.222，在重要性排序中a10比a9重要；a1的平均影響程度為0.122，a6的平均影響程度為0.297，在重要性排序中a6比a1重要。使用同樣的方法可以對決策D2數據表中的4組同等級屬性a7與a8、a6與a1、a4與a9、a3與a10進行計算，通過計算結果可知a7比a8重要，a6比a1重要，a9比a4重要，a10比a3重要。根據上面計算可以對決策D1、D2數據表的屬性再次進行排序，如表8所示。

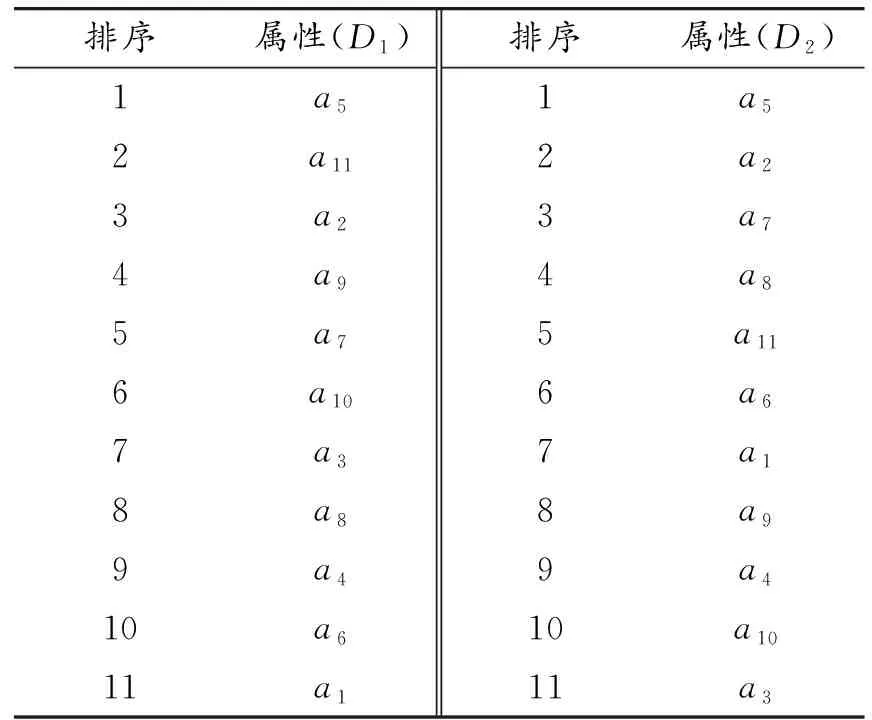
表8 決策表屬性重要性由高到低三級排序

至此，經過粗糙集重要性度量、頻次統計法、影響程度均值法三級排序即實現了所研究問題的數值度量計算，實現了屬性重要性的唯一鏈式排序。11個影響因素對碳排放影響程度的綜合排序結果為：

夏季a5住房面積>a11能耗設備平均使用年限>a2建筑使用時間>a9家庭人均年收入>a7家庭常住人口數>a10節能意識>a3建筑層數>a8最高文化水平>a4所住樓層>a6家庭平均年齡>a1住房歸屬；

冬季a5住房面積>a2建筑使用時間>a7家庭常住人口數>a8最高文化水平>a11能耗設備平均使用年限>a6家庭平均年齡>a1住房歸屬>a9家庭人均年收入>a4所住樓層>a10節能意識>a3建筑層數。

根據實際經驗和相關研究結果可以判斷上述結果的正確和可信，文中所使用的方法科學有效。

5 層級式計算金字塔模型

對本文引用的研究問題，以往研究中普遍使用的方法為調查統計法，需要大量的樣本數據，這些樣本數據需要進行特定的設計和數據處理，還需要假設很多情景和滿足某些要求，其獲取的數據結果基于問卷調查統計結果和統計數據，工作強度大、工作難點多，在屬性排序研究中往往因為各種原因不能很好地進行排序或排序結果不客觀，甚至只是使用分析的方法進行屬性排序，不能很好地做到屬性排序的數量化考量。本文所使用的方法可以免去很多繁瑣的工作，針對所研究問題，獲取采樣數據的規律，這種采樣數據獲取渠道比較簡單和客觀，從獲取的數據表中挖掘潛在的客觀事實，是粗糙集理論應用于創新實踐的一次有益嘗試。本文所用方法獲取的排序結果可以量化處理，排序結果與以往研究方法中獲取的結果一致且優于以往結果，屬性排序結果符合統計規律、經驗和直觀理解。

本文針對研究中遇到的屬性排序問題使用粗糙集方法和統計學方法，分三級量化計算完成屬性重要性程度各級定量計算和全局定性排序。

粗糙集屬性重要度計算方法為初次排序使用方法，使用決策表全局信息計算屬性重要性數值度量，由粗糙集屬性重要度定義直接得到，未進行任何輔助處理，在分層級計算過程中其等級最高，為基于決策表全局宏觀信息的計算，在層級計算過程中排居第1級。

在粗糙集屬性重要度計算不能區分屬性排序的情況下，引進統計學中的頻次統計法，通過可窮舉的約簡中屬性出現的頻次計算數值度量，使用該度量體現屬性的重要性程度，該過程引進統計學方法間接計算，其理論依據扎實可靠，既包含全局約簡的宏觀信息，也包含在約簡中使用統計方法的微觀信息，在層級計算過程中其等級排居第2級。

對于頻次統計結果相同的情況，進一步使用影響程度均值計算法，通過在窮舉的約簡中考慮去掉某屬性后的影響，計算該影響的均值，輔助性區分屬性的重要性程度，該方法使用粗糙集理論中屬性重要度和約簡的意義在所對比屬性所在約簡不完全相同的情況下從微觀角度細分綜合考量屬性的影響程度的均值。均值法和窮舉約簡保證數值度量的客觀性和科學性，計算結果在此步計算中可靠可信，可以區分屬性的重要性程度，因該方法在計算數據過程中不同屬性所在的約簡可能存在差異，故將此方法應用于層級計算的第3級。

針對本文研究的屬性重要性排序層級計算方法，各層級計算的過程包含宏觀到微觀的變化和過渡，每級計算均執行統一度量標準，這種計算過程和每個方法均有理論支撐，包括粗糙集理論、統計學方法、平均值方法等，其層級和執行過程可表示為金字塔形狀，如圖1所示。

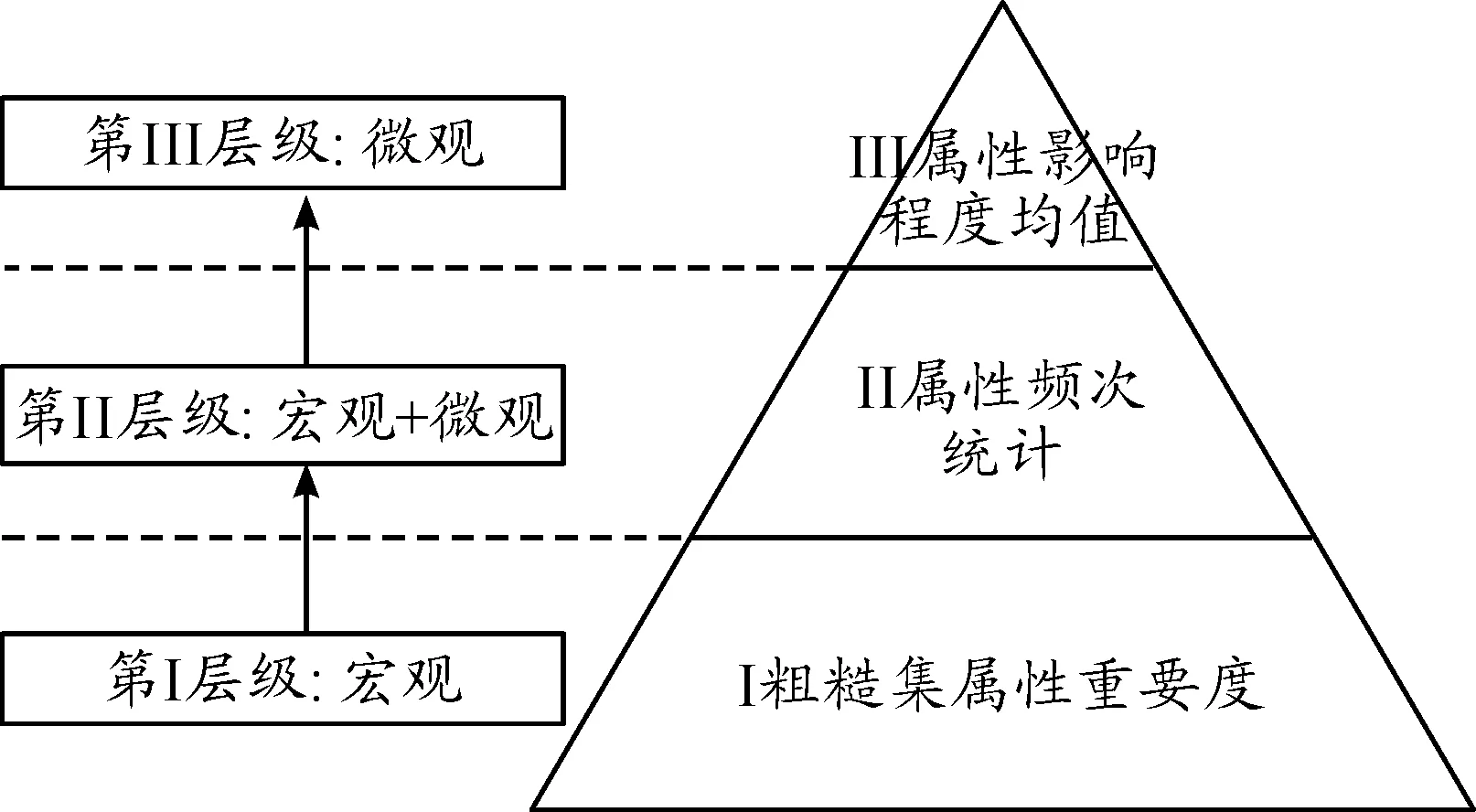
圖1 層級計算金字塔模型

本文所研究層級式解決方法的金字塔表示可以直觀反映各層級計算的等級和權重，執行層級算法的過程實際上是問題由宏觀到微觀細化處理的過程，稱為層級式計算的金字塔模型。在應用問題處理過程中，可以根據需要進行處理，按需選擇是否執行下級計算。

對第1層級的計算方法，除粗糙集理論中最原始的屬性重要度，有可能需要使用其他擴展的重要度計算方法[17]，或者使用信息熵等其他度量，在實際問題中可能需要進行方法的選擇。針對不同問題可能選擇使用不同的粗糙集模型，比如變精度粗糙集、序信息系統、多粒度系統、多論域系統等，其對屬性重要度的計算和層級式計算的細化處理可能有所差別，本文所使用的研究方法和思路均可為各種類似問題提供參考。

6 結束語

針對本文引用的研究問題，通過三級計算的方式，實現了研究問題所需的鏈式唯一排序，對于實際問題的研究具有很重要的突破，使用粗糙集不確定性推理和數據挖掘的理論優勢對所研究問題進行科學處理，獲得了科學、良好的數據結果。本文所研究的方法適用于約簡可以窮舉的決策表；對于約簡不能窮舉的決策表，本文方法具有一定的參考意義。從多數贊成的客觀規律和粗糙集包含度理論的研究角度，對約簡不能窮舉的決策表，本文方法在約簡的使用過程中可以考慮使用可得到的大多數約簡進行計算，其結果也具有一定的參考價值，尤其是在大數據研究中，在進行數據處理時，可能不會使用全部的數據結果(約簡)，使用多數贊成和包含度的處理方法可以實現在不同精度下不精確推理的數據處理。本文研究方法對于應用問題的研究和處理具有很好的參考價值。