脈沖輸入下基于輸入整形法的起重機防搖擺方法
,,
(上海海事大學 航運技術與控制工程交通部重點實驗室,上海 201306)
0 引言
隨著自動化港口的不斷建設和船運業的飛速發展,對于起重機的裝卸效率的要求也越來越高。在起重機運送貨物的過程中,起重機的加減速,風的阻力和負載自身升降都會讓吊重產生搖擺[1],使貨物無法及時到達指定位置,這直接影響了起重機的裝卸效率。目前,大部分的吊車由人工操作,負載的搖擺和起重機的運行也由司機手動控制,運輸的工作效率依賴司機的操作水平,也與碼頭自動化的趨勢相反。所以為了輸送效率的提高及碼頭作業安全,起重機自動防搖擺控制是十分必要的[2]。解決吊重的防搖擺問題對物流運輸行業[3]的發展具有積極的意義[4]。
國內外相關行業和學者已經對防搖控制做了大量的研究,提出了許多方法。按照控制系統的不同進行分類[5],可將防搖控制方法分為兩類:機械式防搖控制法和電子式防搖控制法。其中,電子式防搖控制法又分為開環防搖控制和閉環防搖控制。其區別在于開環[6]控制指控制系統中沒用使用反饋環節來控制擺角;閉環控制[7]指控制系統中含有傳感器來測量起重機的擺角,通過反饋環節控制吊重搖擺的方法[8]。
閉環控制方法中需要利用傳感器采集所需要的信息,例如擺角,加速度等。將數據傳送至處理器的控制部分,由電腦進行計算,得出最佳參數后,實時改變速度。然而此方法中的控制系統設計復雜,參數也會受到工業環境的影響,在實時改變速度時會加速小車零件的老化。并且該方法需要的測量傳感器成本高昂,在實際應用中不易實現,因此限制了該方法在實際生產中的應用。
對于開環控制方法,以加速度輸入的種類不同可以分為階躍輸入法和脈沖輸入法。對于階躍輸入法,上海振華集團[9]提出了兩段加速的控制方法,假設小車系統為無阻尼的二階系統,輸入二段階躍,在3T/4時刻系統擺角回到0,其中T為系統的振蕩周期。在此基礎上,郁春麗[10]研究了階躍輸入下,小車系統為有阻尼的二階系統,并且提出了該系統二段加速,三段加速,……,n段加速控制方法,其中時間最優解在二段加速下達到,擺角在3T/4時刻回到0。對于脈沖輸入法,河南衛華集團[11]的研究是:對于起重機系統,采用黑箱法,不分析其具體的物理特征,以小車的加速度作為輸入,擺角作為輸出,研究了當輸入是二個,三個脈沖時,擺角在T/2,2T/3時刻回到0。
本文將河南衛華集團的二脈沖法、三脈沖法推廣為n脈沖法,研究了不同脈沖下的二階帶阻尼系統的防搖控制性能,以便為用戶提供更多的防搖方法選擇。
1 起重機動態模型分析
考慮到起重機運行中的實際情況,將起重設備中的水平運行的小車,連接負載的繩索和吊重看成一個移動的單擺系統,如圖1所示。
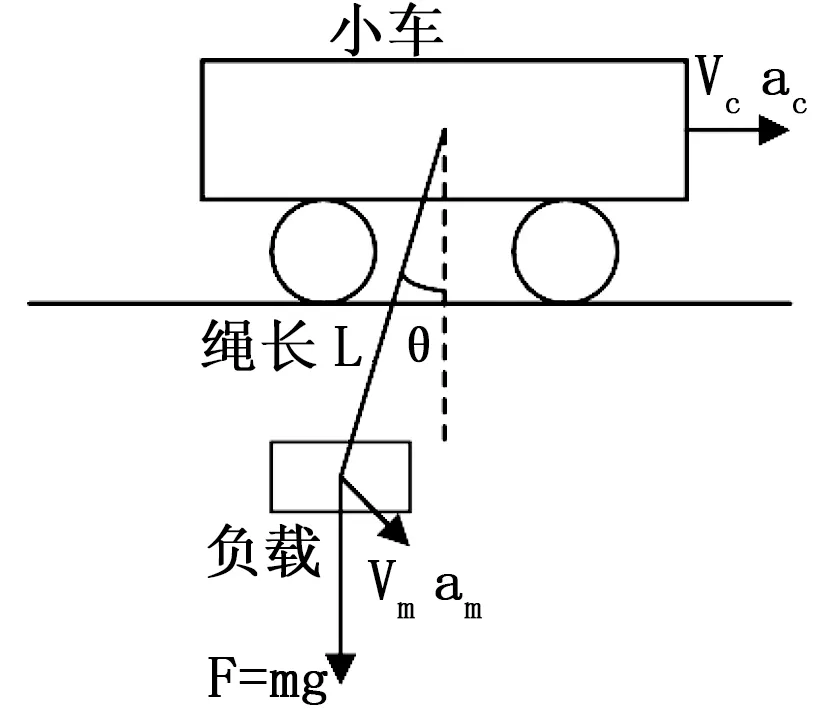

圖1 起重機吊重系統的動力學原理
對以上模型作如下假設:
假設1:小車和負載看作是有一定質量的質點,且起重機靜止不產生相對運動。
假設2:繩索的質量忽略不計,且長度不可拉伸。
假設3:不考慮風力和空氣阻力對負載的影響。
根據牛頓運動定律可得:
(1)
(2)
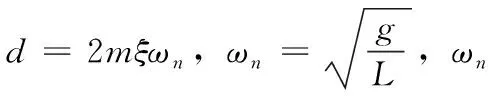
在實際情況下,負載搖擺的角度一般不會超過±10°以內[10],因此可簡化為sinθ≈θ。將式(2)帶入式(1),整理可得:
(3)
(5)
將式(5)進行拉普拉斯變換得:
(6)
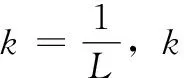
該系統的脈沖響應是:
(7)
2 POSICAST輸入整形開環控制方法
O.J.M.Smith教授在50年代提出了POSICAST控制方法,理論的核心是相隔半周期的正弦函數可以相互抵消。輸入整形法[12]是一種開環控制方法,其技術是將整形器中的脈沖與初始輸入進行卷積計算,將初始輸入整形成防搖需要的脈沖,然后控制整個系統。輸入整形器[13]實際包含不同個數,不同幅值和時滯的序列。這些參數通過動力學模型得到的脈沖響應組成的超越方程求解獲得,通過不同的時間點,給不同幅值的脈沖響應,疊加后的擺角為零。即解下列方程使θ(t)為零:
(8)
其中:ωn為系統固有頻率,ξ為系統阻尼比,n為整形器中脈沖的個數,Ai為脈沖響應的幅值,ti為脈沖響應的延遲時間。
3 起重機防搖擺控制方法
本搖擺控制方法的控制原理來自Smith教授的半周期POSICAST方法,即當第一個脈沖輸入系統后,延遲半個周期后再輸入一個幅值特定的脈沖,去抵消前一個脈沖帶來的擺動,在時刻系統的擺角為零。經過進一步的計算發現,脈沖的個數增加時,恰當的選擇脈沖的幅值,也可以得到良好的防搖效果。下面給出這些控制方法的詳細闡述和理論推導過程
推導過程中涉及到的一些等式如下:
α=ωn*ξ
(9)
(10)
3.1 二脈沖法
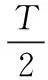
理論解釋:
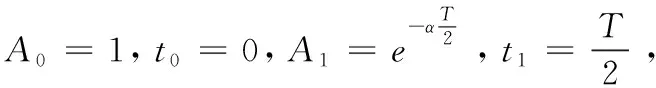
3.2 三脈沖法
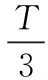
理論解釋:
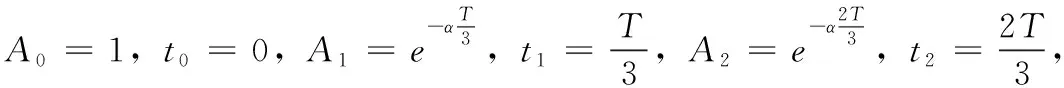
3.3 四脈沖法
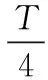
理論解釋:
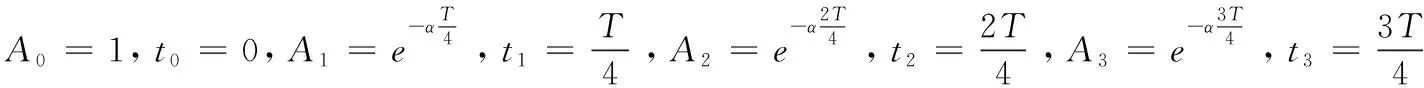
3.4 六脈沖法
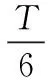
理論解釋:
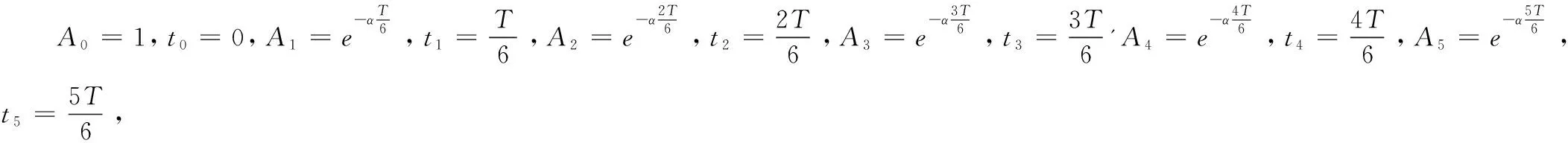
進一步的研究發現,輸入任意個數的脈沖,擺角都可以在適當的時刻回到0。
3.5 n脈沖法
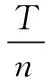
理論解釋:
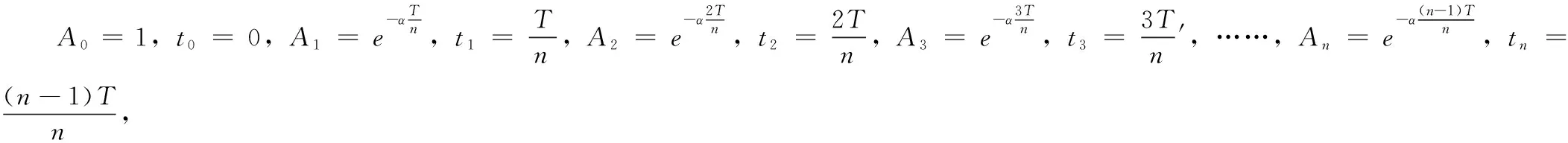
4 基于POSICAST控制方法的仿真驗證
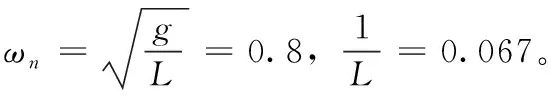
其中:T=7.8 s,α=ωn*ξ=0.0128。
4.1 二脈沖法
該方法中,小車在加速和減速階段時,負載產生搖擺,在勻速行駛和靜止時,負載不產生搖擺。系統的加速度曲線,速度和擺角曲線見圖2。本次仿真中,在加速階段,輸入整形器中加速度脈沖的個數為2,脈沖輸入的時間間隔相等,脈沖的幅值遞減,小車運行中進行兩次加速。小車從靜止到勻速運動,即從吊重開始搖擺到擺角為零所需時間為3.9 s,等于最后一次脈沖輸入的時刻T/2,符合理論計算,運動中小車產生的最大擺角為6.18°。減速階段小車和吊重的情況與加速階段一致。
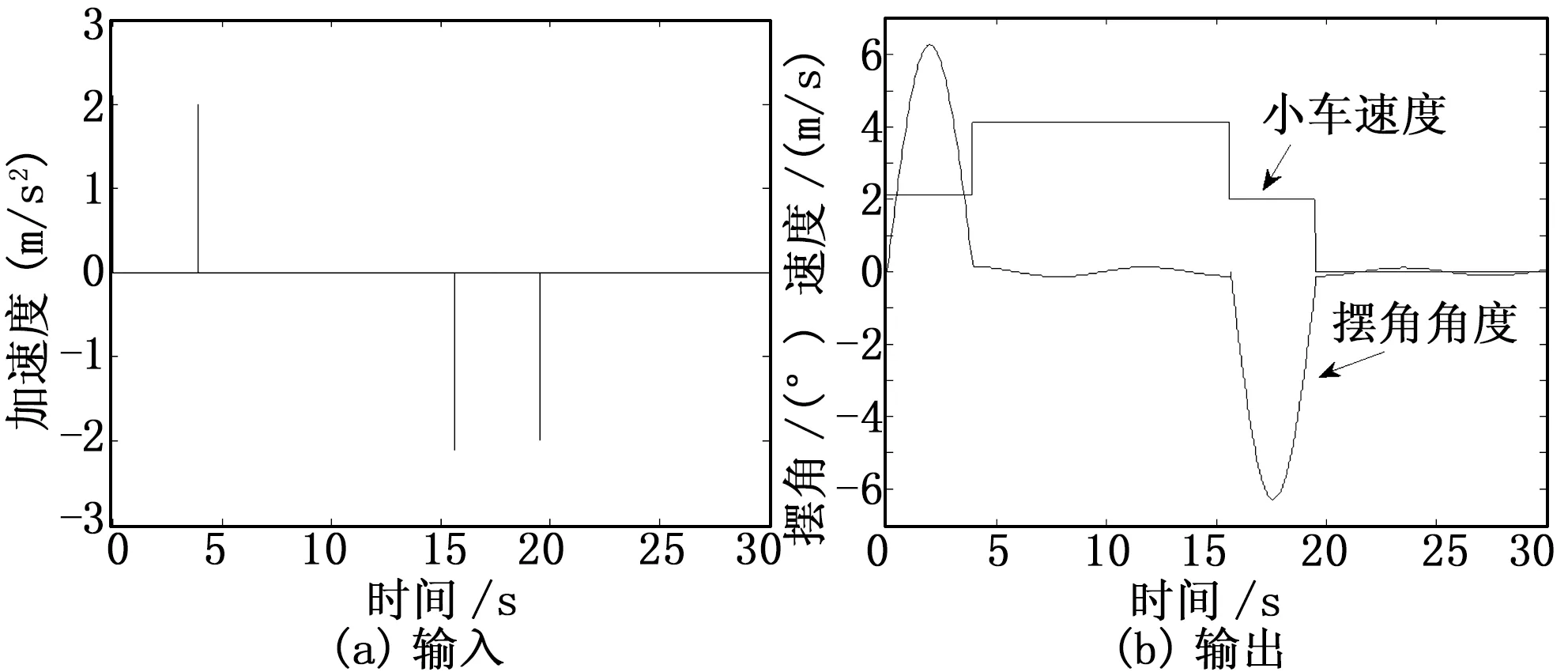
圖2 二脈沖法
4.2 三脈沖法
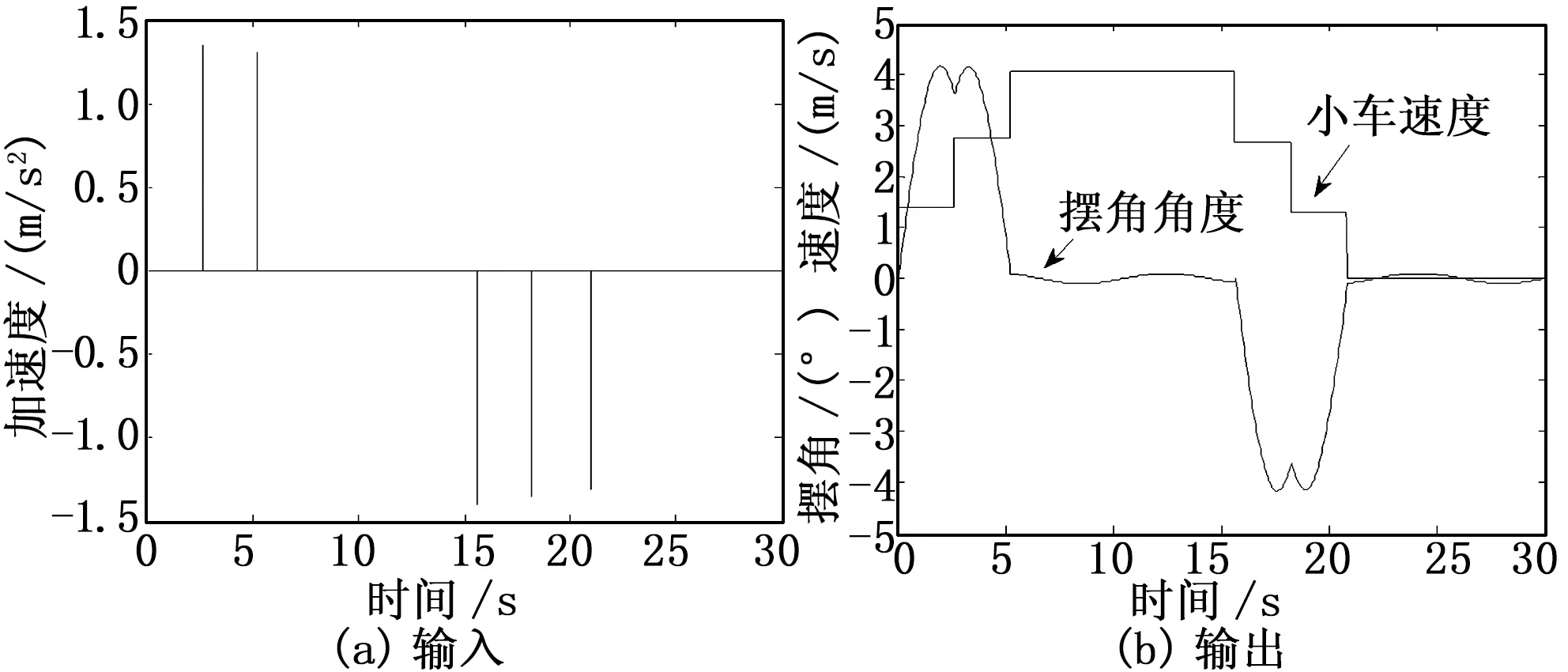
圖3 三脈沖法
4.3 四脈沖法

圖4 四脈沖法
4.4 五脈沖法
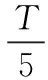
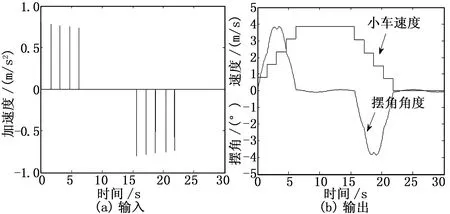
圖5 五脈沖法
4.5 六脈沖法
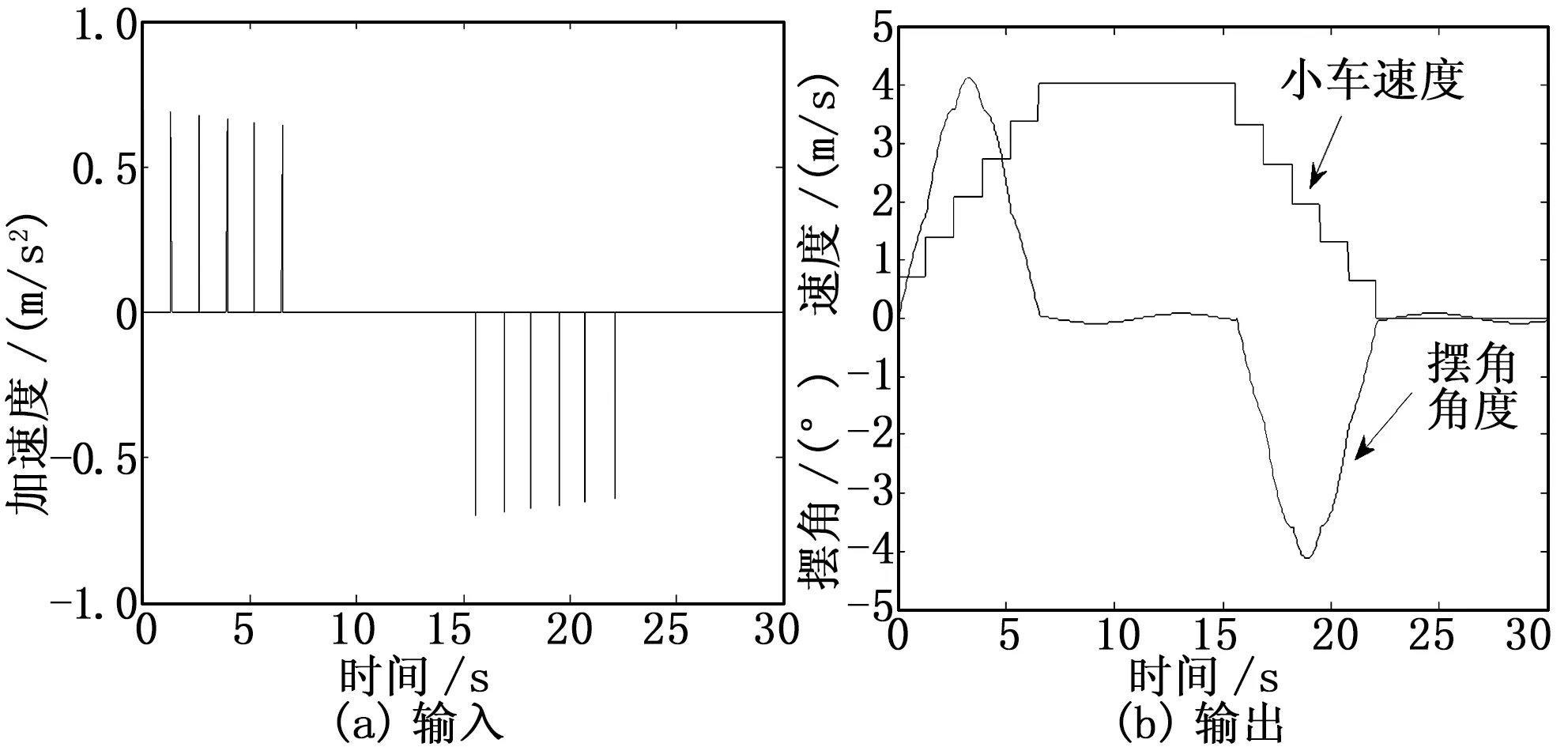
圖6 六脈沖法
從以上的仿真可以看出,二脈沖法的擺角回零時間最短,為T/2,但是產生的最大擺角也最大。
4.6 小結
當輸入為二脈沖到十脈沖,速度最大值和小車擺角最大值及擺角回零時間見表1。
從表1可以看出二脈沖輸入時,負載產生的擺角最大,擺角回到0的時間最短。隨著脈沖個數的增加,最大擺角穩定在4°左右,總體的趨勢是緩慢減少,而回到擺角的時間漸漸增大,越來越趨近于T。在階躍輸入控制法[10]中最優解是,擺角在3T/4時刻回到0,此時擺角的值最大為7.5°;本方法中的最優解是,擺角回零時間縮短為T/2,此時擺角最大為6°。所以相比于階躍輸入法,脈沖輸入法的回零時間減少,最大擺角變小。在實際應用時,可以根據需
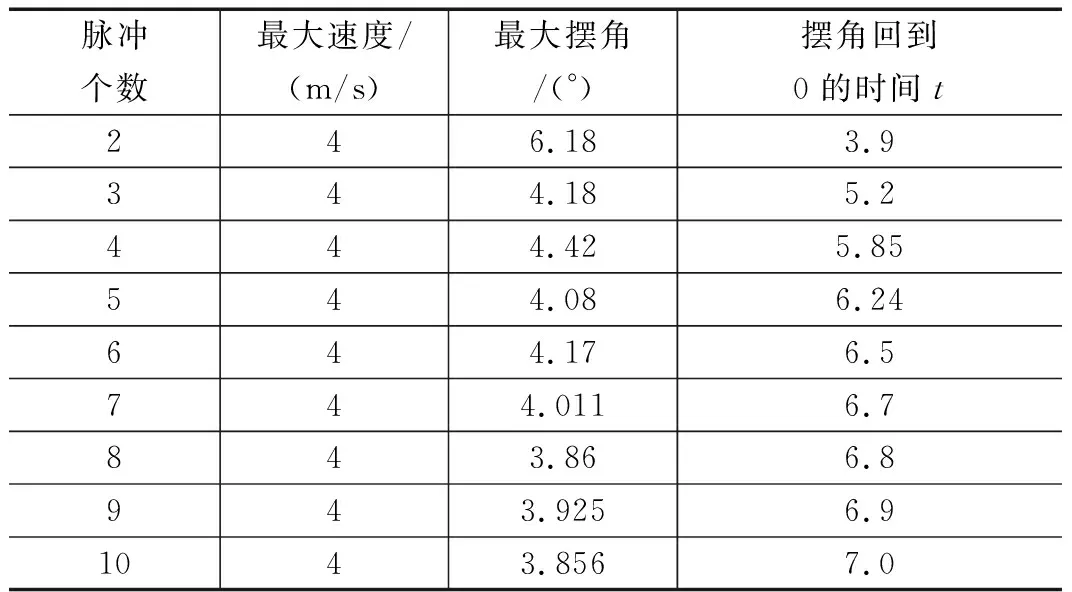
表1 二脈沖法到十脈沖法的防搖特性參數
求和實際情況,選擇不同個數的脈沖對應的脈沖輸入法,控制擺角在相應時間回到0。
5 總結
本文研究了起重機小車運行時吊重的搖擺問題,通過分析小車的動力模型,分析了加速度與擺角的關系,基于輸入整形法,提出了一族脈沖輸入下起重機的電子防搖方法。除了理論計算,還在Matlab中進行了仿真驗證。仿真結果表明,本方法具有良好的防搖效果。

