高考數學創新型試題的幾種類型
■河南省信陽高級中學 陳榮軍
高校要選拔具有創新潛質的人才,高考數學必須重視對學生創新意識的考查。考生的創新意識表現為:對新穎的信息、情境的設問,能選擇有效的方法和手段分析、處理信息,綜合與靈活地應用所學的數學知識、思想和方法,進行獨立的思考、探索和研究,提出解決問題的思路,并創造性地解決問題。近幾年來,在全國及各省市的各套高考數學試卷中出現了一些創新型試題,這些試題主要類型有直覺思維型、學習遷移型、實際應用型等。本文擬對高考數學創新型試題的類型作一些分析。
一、直覺思維型
直覺思維是指個體以已有的知識經驗為基礎,無須邏輯推理,對突然出現的新問題和新現象,能迅速理解并作出判斷的思維方式。直覺思維可以幫助同學們洞察數學本質、猜想數學結論、發現數學規律等。直覺思維是快速解答一些高考數學試題的利器。鑒于直覺思維的重要作用,在高考數學試題的命制中,很自然地要考查同學們的直覺思維。直覺思維型的試題主要有整體觀察型、直覺判斷型、類比聯想型、歸納猜想型、極限洞察型等。
例1 四位好朋友在一次聚會上,他們按照各自的愛好選擇了形狀不同、內空高度相等、杯口半徑相等的圓口酒杯,如圖1所示。
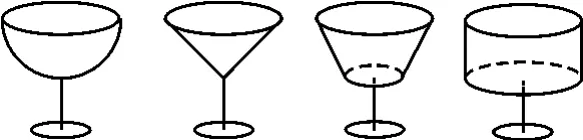
圖1
盛滿酒后他們約定:先各自飲杯中酒的一半。設剩余酒的高度從左到右依次為h1,h2,h3,h4,則它們的大小關系是( )。
A.h2>h1>h4B.h1>h2>h3
C.h3>h2>h4D.h2>h4>h1
點評:本題背景鮮活,頗有生活氣息。命題者大膽地將四種旋轉體匯集在一起,與日常生活中的酒杯形狀聯系起來,巧妙設問,主要考查幾何體的體積與高度的關系,考查同學們的空間想象能力及直覺思維能力。通過整體觀察,不需具體計算,進行直覺思維,對問題作出迅速、準確的直覺判斷。因為各酒杯杯口半徑相等,即上底面積相等。內空高度相等,且飲去上部一半,故下部越細,剩余酒高度越高,所以有h2>h1>h4。故選A。

圖2
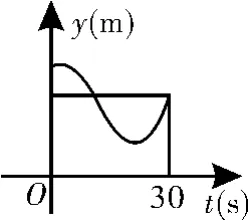
圖3
跟蹤練習1 小明在如圖2所示的跑道上勻速跑步,他從點A出發,沿箭頭方向經過點B跑到點C,共用時3 0s,他的教練選擇了一個固定的位置觀察小明跑步的過程,設小明跑步的時間為t(s),他與教練間的距離為y(m),表示y與t的函數關系的圖像大致如圖3所示,則這個固定位置可能是圖2中的( )。
A.點 M B.點 N
C.點P D.點Q
解析:分別假設這個位置在點M、N、P、Q,然后結合函數圖像進行判斷,利用排除法即可得出答案。選項A,假設在M處,則A至B段y為常數,與函數圖像不符,故A錯誤。選項B,假設在N處,則A與C處y的值相同,與函數圖像不符,故B錯誤。選項C,假設在P處,則3 0s時y的值最小,與函數圖像不符,故C錯誤。經判斷點Q符合函數圖像。故選D。
二、學習遷移型
解答學習遷移型試題 ,需要同學們具有自主學習和遷移的能力。學習能力是同學們閱讀并理解數學新知識的能力,這里的新知識可以是新的概念、新的定理、新的方法、新的公式、新的規則等。學習能力包括會搜集、提煉、加工信息,對閱讀的內容進行概括和理解,看清問題的本質,然后運用新的知識通過分析、演算、歸納、猜想、類比或論證等方法解決一些新的數學問題。
例2 設P是一個數集,且至少含有兩個數,若對任意a、b∈R,都有a+b、a-b、數b≠0),則稱P是一個數域。例如有理數集Q是數域;數集F={a+b2|a,b∈Q}也是數域。有下列命題:
點評:本題設計獨特、情境新穎,具有很強的抽象性和發散性。從試題的背景來看,此題以近世代數中“群、環、域”的知識為背景,試題展示給同學們的是一個全新的問題,體現了自主學習和主動探究精神。從試題的立意來看,本題是一道能有效考查同學們的閱讀理解能力、抽象與具體轉化能力、構造法和反例思想方法的創新型試題。從試題的解答來看,直接以“數域”的定義為背景的試題在各種復習資料和模擬試題中從未見過,解決這個問題沒有現成的套路和招式,需要同學們閱讀理解“數域”的定義,綜合運用多種數學思想方法,分別檢查所給答案是否同時滿足“數域”定義的四個條件(滿足需證明,不滿足需舉反例),才能解決問題。這類以高等數學知識為背景的問題,能有效考查同學們進一步學習的潛質,已成為高考試題的一大亮點和熱點,值得注意。
跟蹤練習2 對定義在區間D上的函數f(x),若存在常數k>0,使對任意的x∈D,都有f(x+k)>f(x)成立,則稱f(x)為區間D上的“k階增函數”。已知f(x)是定義在R上的奇函數,且當x≥0,f(x)=|xa2|-a2。若f(x)為R上的“4階增函數”,則實數a的取值范圍是____。
解析:當x≥0,f(x)=|x-a2|-a2時,令f(x)=0,則y=f(x)有最大的零點是2a2,由y=f(x)是奇函數,所以y=f(x)有最小的零點是-2a2。把橫坐標向左平移4個單位得到y=f(x+4)的圖像,且y=f(x+4)有最大的零點為2a2-4。因為y=f(x)為R上的 “4階增函數”,則對任意的x∈R,都有f(x+4)>f(x)恒成立,即函數y=f(x+4)的圖像在函數y=f(x)的圖像上方,由圖4可知,2a2-4<-2a2,即a2<1,故a的取值范圍是(-1,1)。

圖4
三、實際應用型
“堅持數學應用,考查應用意識”是多年以來一貫堅持的命題方針。應用題是對同學們“綜合實力”的考查,是考查能力與素質的良好題型,近幾年應用題的編擬更加重視語言簡潔、準確,背景清新、近人,模型具體、簡明,方法熟悉、簡便,所涉及的都是數學基本內容、思想和方法,摒棄煩瑣的數學運算,突出對數學思想、方法和實踐能力的考查,彰顯數學在解決實際問題中的重要作用。
例3 圖5是某汽車維修公司的維修點環形分布圖。公司在年初分配給A、B、C、D四個維修點某種配件各5 0件。在使用前發現需將A、B、C、D四個維修點的這批配件分別調整為4 0、4 5、5 4、6 1件,但調整只能在相鄰維修點之間進行。那么要完成上述調整,最少的調動件次(n件配件從一個維修點調整到相鄰維修點的調動件次為n)為( )。
A.1 5 B.1 6 C.1 7 D.1 8
解析:D處的零件要從A、C或B處移來調整,且次數最少。方案一:從A處調1 0個零件到D處,從B處調5個零件到C處,從C處調1個零件到D處,共調動1 6件次。方案二:從B處調1個零件到A處,從A處調1 1個零件到D處,從B處調4個零件到C處,共調動1 6件次。故選B。
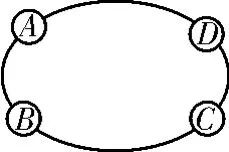
圖5
點評:本題是一個優化安排的問題,需要同學們綜合運用已有的知識經驗,通過各種調整的操作試驗與嘗試才能解決問題。此題提高了對分析問題和解決問題的能力要求,大大增加了思維量,很好地考查了同學們的實踐能力和數學應用意識。
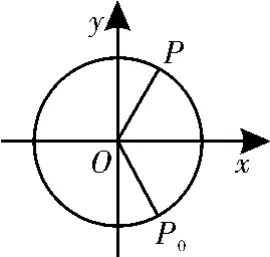
圖6
跟蹤練習3 如圖6,質點P在半徑為2的圓周上逆時針運動,其初始位置為P0,-),角速度為1,那么點P到x軸的距離d關于時間t的函數圖像大致為圖7中的( )。
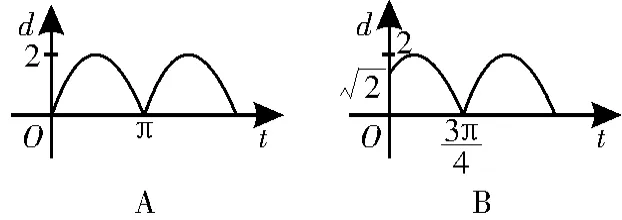
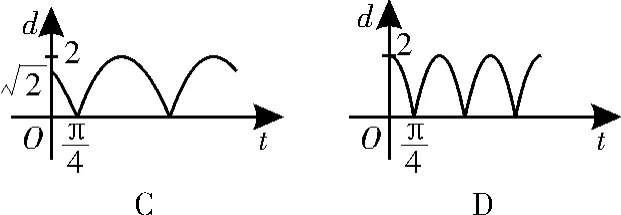
圖7
解法一:(排除法)當t=0時,P點到x軸的距離為2,排除A、D,由角速度為1知,落在x軸上,即P點到x軸的距離為0。故選C。

